Topic is 324 a square number: Is 324 a square number? Yes, it is! In this article, we will explore why 324 is a perfect square, delving into its mathematical properties, prime factorization, and real-life applications. Join us on this educational journey to uncover the intriguing aspects of square numbers and their significance in mathematics.
Table of Content
- Is 324 a Square Number?
- Introduction to Square Numbers
- Understanding the Concept of a Square Number
- Mathematical Definition of a Square Number
- Is 324 a Square Number?
- Prime Factorization of 324
- Properties of the Number 324
- Square Root Calculation
- Visual Representation of Square Numbers
- Examples of Square Numbers
- Applications of Square Numbers in Real Life
- Conclusion
- YOUTUBE:
Is 324 a Square Number?
Yes, 324 is a square number.
Explanation
A square number, also known as a perfect square, is an integer that is the square of another integer. In other words, a number n is a square number if there exists an integer m such that:
\[ n = m^2 \]
For the number 324, we can find the integer m as follows:
\[ 324 = 18^2 \]
Therefore, 324 is the square of 18, making it a square number.
Properties of 324
- Square Root: The square root of 324 is 18.
- Even Number: 324 is an even number.
- Composite Number: 324 is a composite number, meaning it has more divisors other than 1 and itself.
Steps to Determine if 324 is a Square Number
- Find the prime factorization of 324.
- 324 = 2 × 2 × 3 × 3 × 3 × 3
- Group the prime factors into pairs.
- (2 × 2) and (3 × 3) and (3 × 3)
- If all prime factors can be grouped into pairs, the number is a perfect square.
- Since all prime factors of 324 can be grouped into pairs, it confirms that 324 is a square number.
Visual Representation
The number 324 can be represented as a 18x18 grid:
| 18 | x | 18 | = | 324 |
READ MORE:
Introduction to Square Numbers
Square numbers, also known as perfect squares, are integers that can be expressed as the product of an integer with itself. In mathematical terms, a number n is a square number if there exists an integer m such that:
\[ n = m^2 \]
Understanding square numbers is fundamental in various areas of mathematics, including algebra, number theory, and geometry. They have unique properties and play a crucial role in solving equations and understanding the structure of numbers.
Here is a step-by-step breakdown of the concept of square numbers:
- Identify the integer m.
- Multiply the integer by itself to get n.
- Example: If m is 5, then \( 5 \times 5 = 25 \). Therefore, 25 is a square number.
- Check if the number can be decomposed into equal factors.
- Example: 36 can be written as \( 6 \times 6 \), making 36 a perfect square.
Square numbers have several interesting properties:
- They have an odd number of total divisors.
- They can be represented as a sum of consecutive odd numbers.
- The difference between consecutive square numbers follows a specific pattern.
Understanding square numbers helps in recognizing patterns, simplifying expressions, and solving quadratic equations. They are also visually represented in the form of squares, which makes them easy to comprehend and relate to geometrically.
Understanding the Concept of a Square Number
A square number, or perfect square, is an integer that results from multiplying an integer by itself. This can be represented mathematically as:
\[ n = m^2 \]
where n is the square number and m is the integer whose product with itself gives n.
To understand this concept better, let's explore it step by step:
- Choose an integer m.
- Example: Let m be 18.
- Multiply m by itself to find n.
- \[ 18 \times 18 = 324 \]
- Thus, 324 is a square number because it can be written as \( 18^2 \).
- Verify that the multiplication results in an integer.
- If \( m^2 \) is an integer, then n is a perfect square.
Square numbers have unique properties that set them apart:
- Number of Divisors: A perfect square has an odd number of divisors. For example, 324 has 15 divisors.
- Sum of Odd Numbers: A square number can be represented as the sum of consecutive odd numbers. For instance: \[ 324 = 1 + 3 + 5 + \ldots + 35 \]
- Geometric Representation: Square numbers can be visually represented as squares. For example, 324 can be depicted as an 18 by 18 grid.
- Difference of Squares: The difference between consecutive square numbers follows the pattern: \[ (m+1)^2 - m^2 = 2m + 1 \] For example: \[ 19^2 - 18^2 = 361 - 324 = 37 \]
By recognizing and understanding these properties, one can easily identify and work with square numbers in various mathematical contexts. Square numbers are foundational in algebra, number theory, and geometry, making them a vital part of mathematical education and application.
Mathematical Definition of a Square Number
A square number, also known as a perfect square, is an integer that can be expressed as the product of an integer with itself. Mathematically, a number n is a square number if there exists an integer m such that:
\[ n = m^2 \]
This means that n is the result of multiplying the integer m by itself. To further understand this, let's break down the concept step by step:
- Identify an integer m.
- Example: Let m be 18.
- Multiply the integer by itself to find n.
- \[ 18 \times 18 = 324 \]
- Hence, 324 is a square number because it equals \( 18^2 \).
Square numbers have several interesting mathematical properties:
- Non-negative: Square numbers are always non-negative because the product of two integers with the same sign is positive.
- Odd and Even: A square number can be even or odd. If m is even, then \( m^2 \) is even. If m is odd, then \( m^2 \) is odd.
- Sum of Consecutive Odd Numbers: Any square number can be expressed as the sum of consecutive odd numbers. For instance:
- \[ 324 = 1 + 3 + 5 + \ldots + 35 \]
- Divisors: Square numbers have an odd number of divisors. For example, 324 has 15 divisors.
These properties make square numbers significant in various mathematical contexts. They are essential in solving equations, understanding number patterns, and exploring geometric relationships. Recognizing square numbers and their characteristics allows for deeper insights into the structure and behavior of numbers in mathematics.
Is 324 a Square Number?
Yes, 324 is a square number. To understand why, let's go through the detailed steps to verify this:
- Identify if there exists an integer m such that: \[ 324 = m^2 \]
- Calculate the square root of 324.
- The square root of 324 is: \[ \sqrt{324} = 18 \]
- Verify the calculation:
- Multiply 18 by itself: \[ 18 \times 18 = 324
Since 18 multiplied by itself equals 324, it confirms that 324 is a perfect square.
Let's explore the properties of 324 as a square number:
- Even Number: 324 is an even number because it ends in 4.
- Divisors: 324 has an odd number of divisors, which is a characteristic of square numbers. The divisors of 324 are:
- 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, and 324
- Prime Factorization: The prime factorization of 324 is: \[ 324 = 2^2 \times 3^4 \]
- Geometric Representation: 324 can be represented as an 18 by 18 grid, illustrating it as a perfect square visually.
Square numbers like 324 are significant in various mathematical applications and problem-solving scenarios. They provide insights into number patterns, properties of integers, and are essential in fields such as algebra and geometry.

Prime Factorization of 324
Prime factorization is the process of breaking down a composite number into a product of its prime factors. To determine the prime factorization of 324, we will follow a step-by-step process:
- Divide 324 by the smallest prime number, which is 2.
- \[ 324 \div 2 = 162 \]
- Continue dividing the quotient by 2 until it is no longer divisible by 2.
- \[ 162 \div 2 = 81 \]
- Next, divide the quotient by the next smallest prime number, which is 3.
- \[ 81 \div 3 = 27 \]
- Continue dividing by 3 until it is no longer divisible by 3.
- \[ 27 \div 3 = 9 \] \[ 9 \div 3 = 3 \] \[ 3 \div 3 = 1 \]
By dividing 324 step-by-step by its prime factors, we get the prime factorization:
\[
324 = 2^2 \times 3^4
\]
Let's summarize the prime factorization in a table format:
| Step | Division | Result |
|---|---|---|
| 1 | 324 ÷ 2 | 162 |
| 2 | 162 ÷ 2 | 81 |
| 3 | 81 ÷ 3 | 27 |
| 4 | 27 ÷ 3 | 9 |
| 5 | 9 ÷ 3 | 3 |
| 6 | 3 ÷ 3 | 1 |
Thus, the prime factors of 324 are 2 and 3, and the prime factorization is expressed as \( 2^2 \times 3^4 \). Understanding the prime factorization of numbers like 324 is essential in various areas of mathematics, including simplifying fractions, finding the greatest common divisor (GCD), and solving problems involving ratios.
Properties of the Number 324
The number 324 has several interesting mathematical properties:
- Square Number: 324 is a perfect square, as it can be expressed as \(18^2\) (18 multiplied by itself).
- Even Number: 324 is an even number, as it is divisible by 2.
- Composite Number: 324 is a composite number, meaning it has factors other than 1 and itself.
- Prime Factorization: The prime factorization of 324 is \(2^2 \times 3^4\).
- Divisors: The number 324 has 15 divisors: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 324.
- Sum of Divisors: The sum of all divisors of 324 is 847.
- Digits: The digits of 324 add up to 9 (3 + 2 + 4 = 9).
The table below summarizes the key properties of 324:
| Property | Value |
| Square Number | \(18^2\) |
| Even Number | Yes |
| Composite Number | Yes |
| Prime Factorization | \(2^2 \times 3^4\) |
| Number of Divisors | 15 |
| Sum of Divisors | 847 |
| Sum of Digits | 9 |
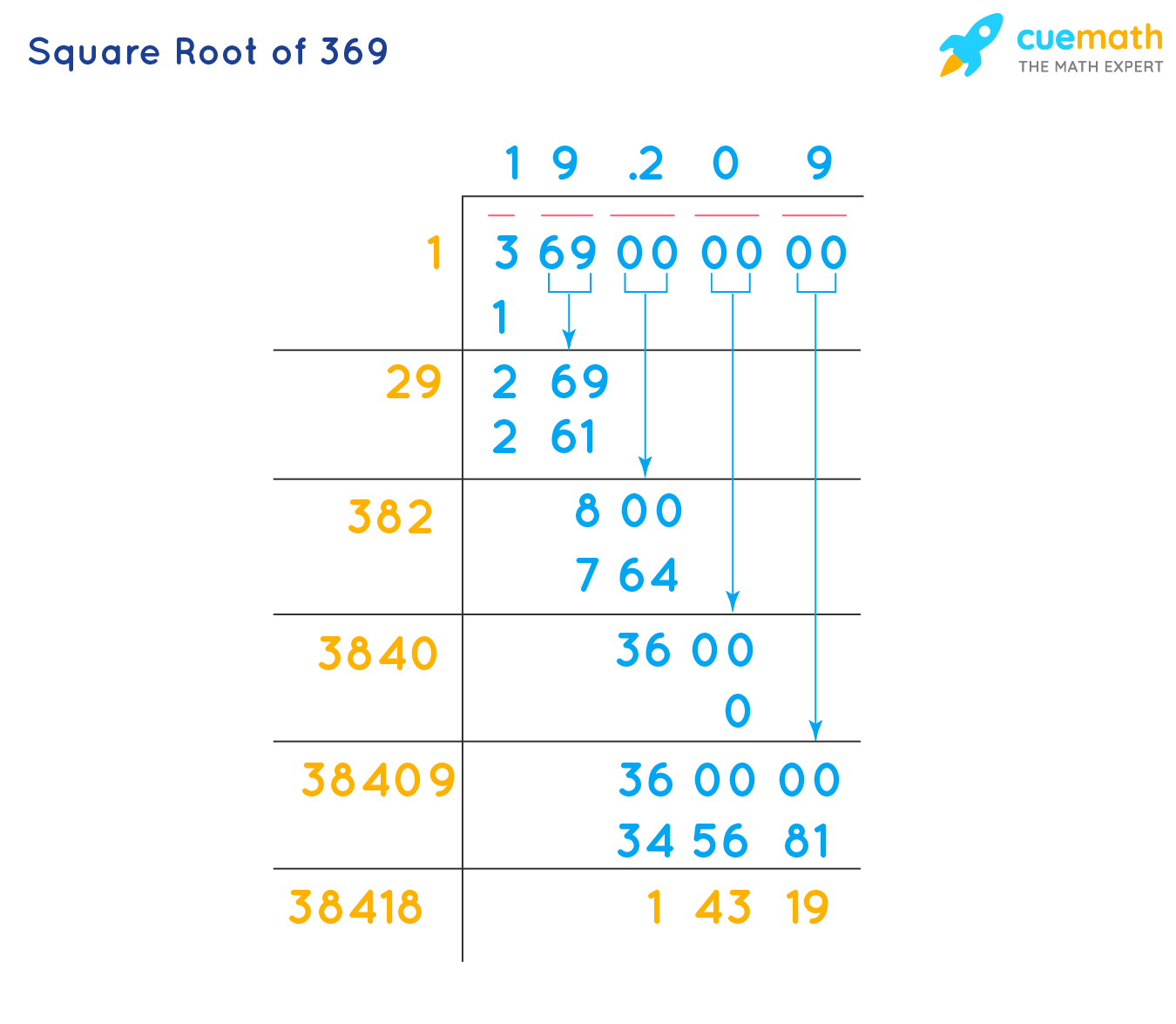
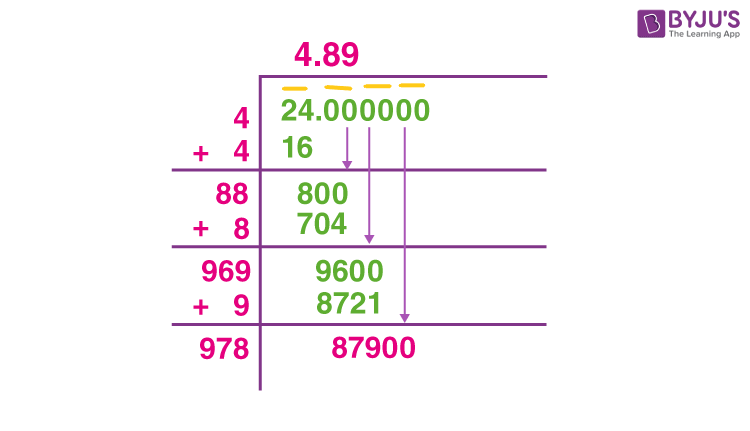
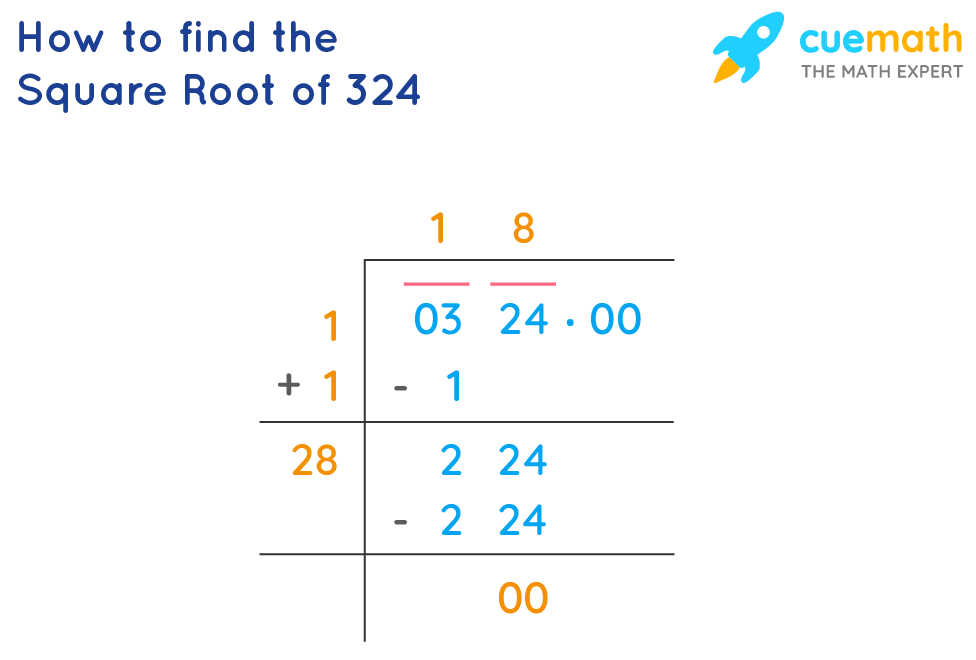
Square Root Calculation
Calculating the square root of 324 involves the following steps:
-
Understand the square root:
The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). In this case, we need to find \( y \) such that \( y^2 = 324 \).
-
Prime factorization of 324:
Begin by breaking down 324 into its prime factors:
\[
324 = 2^2 \times 3^4
\] -
Pair the prime factors:
To find the square root, pair the prime factors:
\[
\sqrt{324} = \sqrt{2^2 \times 3^4} = \sqrt{(2 \times 2) \times (3 \times 3 \times 3 \times 3)} = 2 \times 3^2 = 2 \times 9 = 18
\] -
Verification:
Square the result to verify the calculation:
\[
18 \times 18 = 18^2 = 324
\]
Thus, the square root of 324 is \( \sqrt{324} = 18 \). This confirms that 324 is a perfect square, as its square root is an integer.
Visual Representation of Square Numbers
Visualizing square numbers can help in understanding their properties. Here’s how to represent square numbers visually:
-
Square Grid Representation:
A square number can be represented as a grid of dots or squares, where the number of dots along each side of the grid is equal to the square root of the number. For example, 324 can be represented as a grid with 18 dots along each side:
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • • -
Geometric Square Representation:
Another way to visualize square numbers is through geometric shapes. A perfect square forms a larger square when small identical squares are arranged in rows and columns. For 324, arrange 324 unit squares in an 18x18 grid to form a larger square.
-
Area Representation:
Consider a square with side length 18 units. The area of this square is calculated as:
\[
\text{Area} = 18 \times 18 = 324 \, \text{square units}
\]This visual representation helps in understanding that 324 is a perfect square, as it can be formed by multiplying the side length by itself.
These visual methods aid in comprehending the concept of square numbers and illustrate why 324 is a perfect square.
Examples of Square Numbers
Square numbers are integers that can be expressed as the product of an integer with itself. Here are some examples of square numbers and how they are calculated:
-
1:
\[
1^2 = 1 \times 1 = 1
\] -
4:
\[
2^2 = 2 \times 2 = 4
\] -
9:
\[
3^2 = 3 \times 3 = 9
\] -
16:
\[
4^2 = 4 \times 4 = 16
\] -
25:
\[
5^2 = 5 \times 5 = 25
\] -
36:
\[
6^2 = 6 \times 6 = 36
\] -
49:
\[
7^2 = 7 \times 7 = 49
\] -
64:
\[
8^2 = 8 \times 8 = 64
\] -
81:
\[
9^2 = 9 \times 9 = 81
\] -
100:
\[
10^2 = 10 \times 10 = 100
\] -
121:
\[
11^2 = 11 \times 11 = 121
\] -
144:
\[
12^2 = 12 \times 12 = 144
\] -
169:
\[
13^2 = 13 \times 13 = 169
\] -
196:
\[
14^2 = 14 \times 14 = 196
\] -
225:
\[
15^2 = 15 \times 15 = 225
\] -
256:
\[
16^2 = 16 \times 16 = 256
\] -
289:
\[
17^2 = 17 \times 17 = 289
\] -
324:
\[
18^2 = 18 \times 18 = 324
\]
These examples illustrate that square numbers are the result of multiplying an integer by itself. Recognizing these patterns can help in identifying square numbers and understanding their properties.
Applications of Square Numbers in Real Life
Square numbers have various practical applications in everyday life and different fields. Here are some examples of how square numbers are used:
-
Geometry and Area Calculation:
In geometry, square numbers are used to calculate the area of squares. The area of a square is given by the side length squared. For example, a square with a side length of 18 units has an area of:
\[
\text{Area} = 18^2 = 324 \, \text{square units}
\] -
Architecture and Design:
Architects and designers use square numbers to create aesthetically pleasing and structurally sound designs. Square and rectangular shapes based on square numbers ensure balance and proportion in constructions.
-
Sports and Games:
Many sports fields and game boards are designed using square numbers. For example, a standard chessboard has 8 squares on each side, resulting in:
\[
8^2 = 64 \, \text{squares}
\] -
Digital Imaging and Pixels:
Square numbers are crucial in digital imaging, where the resolution of an image is often expressed in terms of pixels. For example, a 324x324 pixel image has a total of:
\[
324 \times 324 = 104976 \, \text{pixels}
\] -
Data Organization:
Square numbers are used in organizing data in grids and matrices, which is important for computer science, statistics, and various analytical applications.
-
Urban Planning:
City planners use square numbers to design grids for streets, plots, and blocks, ensuring efficient use of space and easy navigation.
-
Financial Calculations:
In finance, square numbers are used in various formulas, such as calculating the square root of the variance to determine the standard deviation, which is a measure of risk.
These examples demonstrate how square numbers are integral to various real-life applications, from basic geometry to advanced scientific calculations.
Conclusion
Understanding square numbers and their properties is fundamental to various mathematical concepts and real-life applications. The number 324 is a perfect square, as it can be expressed as \( 18^2 \). We have explored several aspects of square numbers, including their mathematical definition, properties, and practical applications.
Through the process of determining if 324 is a square number, we learned to calculate the square root and verified that the square root of 324 is indeed 18. This verification involved breaking down the number into its prime factors and demonstrating that the product of these factors yields the original number.
Visual representations, such as grid and geometric square representations, help to illustrate why 324 is a perfect square. By seeing these visual aids, we can better grasp the concept and recognize other square numbers more easily.
Examples of square numbers, ranging from 1 to 324, highlight the pattern and growth of these numbers. They provide a clear understanding of how square numbers are formed and how they fit into the broader scope of mathematics.
The practical applications of square numbers in areas like geometry, architecture, digital imaging, and financial calculations demonstrate their importance beyond theoretical math. Square numbers are integral to many aspects of our daily lives, from the design of buildings and cities to the organization of data and the analysis of financial risks.
In conclusion, the study of square numbers, including the specific case of 324, reveals their significance and utility. By mastering this concept, we gain valuable insights that enhance our mathematical knowledge and its application in various fields.
Cách Tìm Căn Bậc Hai của 324 bằng Phân Tích Thừa Số Nguyên Tố / Căn Bậc Hai của 324 / Căn Bậc Hai 324
READ MORE:
Tìm hiểu xem 324 có phải là số chính phương hay không qua video này. Khám phá câu trả lời chi tiết và chính xác.
324 có phải là số chính phương?