Topic simplify square root of 61: Unlock the secrets of simplifying the square root of 61 in this comprehensive guide. Understand the exact and decimal forms, explore prime factorization, and learn practical applications. Dive into the mathematical properties of √61 and discover its significance in various contexts, making complex concepts easy to grasp.
Table of Content
- Simplifying the Square Root of 61
- Introduction to Square Roots
- Understanding the Square Root of 61
- Exact Form of √61
- Decimal Representation of √61
- Exponent Form of √61
- Steps to Simplify Square Root of 61
- Prime Factorization Method
- Perfect Squares and Simplification
- Properties of Square Root of 61
- Square Root of 61 in Various Mathematical Forms
- Applications of √61 in Real Life
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Tìm hiểu cách đơn giản hóa √(61 + 28√(3)) và √(3.5 + √(10)) trong video hướng dẫn này. Khám phá phương pháp và kỹ thuật để làm chủ số học và các phương trình phức tạp.
Simplifying the Square Root of 61
The square root of 61 is an interesting number to consider, as 61 is a prime number. This means that it does not have any perfect square factors other than 1 and itself. Therefore, the square root of 61 cannot be simplified into a smaller radical form.
Exact and Decimal Form
The square root of 61 in its exact form is simply √61. When expressed as a decimal, it is approximately:
7.8102496759067
Exponent Form
In exponent form, the square root of 61 can be written as:
611/2
Steps to Simplify the Square Root
- List the factors: The factors of 61 are 1 and 61.
- Identify perfect squares: The only perfect square among the factors is 1.
- Conclusion: Since there are no other perfect square factors, √61 is already in its simplest form.
Understanding Prime Factorization
As 61 is a prime number, it cannot be broken down into smaller factors other than 1 and 61 itself. This means that there are no smaller square roots that can multiply to give 61.
Additional Information
- The square root of 61 is an irrational number because it cannot be expressed as a fraction of two integers.
- In terms of algebraic operations, the square root of 61 multiplied by itself gives the original number 61:
√61 × √61 = 61
While we can't simplify √61 further, understanding its properties and representation in different forms can be useful for various mathematical applications.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, representing the inverse operation of squaring a number. When you square a number, you multiply it by itself. Conversely, finding the square root of a number means determining which number, when squared, equals the original number.
For example, the square root of 9 is 3, because \( 3 \times 3 = 9 \). Similarly, the square root of 16 is 4, because \( 4 \times 4 = 16 \).
The square root of a number is denoted using the radical symbol \( \sqrt{} \). If the number under the radical is not a perfect square, its square root is an irrational number, which cannot be expressed as a simple fraction.
Let's consider the square root of 61:
- The square root of 61 is represented as \( \sqrt{61} \).
- Since 61 is a prime number, it does not have any perfect square factors other than 1.
- This means \( \sqrt{61} \) is already in its simplest radical form.
- In decimal form, the square root of 61 is approximately 7.810.
- In exponential form, it is represented as \( 61^{\frac{1}{2}} \).
Understanding square roots is crucial for solving quadratic equations, working with geometric shapes, and various applications in science and engineering. Recognizing the properties of numbers, such as whether they are prime or composite, helps in simplifying square roots effectively.
While simplifying the square root of 61 does not yield a simpler radical, recognizing its approximate decimal value and its properties aids in various mathematical contexts.
Understanding the Square Root of 61
The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 61, denoted as √61, is a value which satisfies the equation \( \sqrt{61} \times \sqrt{61} = 61 \). Understanding and simplifying square roots is a fundamental concept in mathematics, useful in various applications.
To simplify a square root, you typically look for factors of the number that are perfect squares. However, 61 is a prime number, meaning it has no factors other than 1 and 61 itself, and there are no perfect square factors. Hence, the square root of 61 cannot be simplified further and remains as √61.
When expressed in decimal form, √61 approximately equals 7.81025. This is useful for practical calculations where an exact root is not necessary.
To summarize:
- The exact form of the square root of 61 is √61.
- The decimal form of √61 is approximately 7.81025.
Understanding these basics helps in recognizing that some square roots cannot be simplified into a more manageable form, emphasizing the importance of prime factorization and properties of numbers.
Exact Form of √61
The square root of 61 is an irrational number, meaning it cannot be simplified into a precise fractional or integer form. To express √61 exactly, we keep it in its radical form.
Here's a step-by-step breakdown:
-
Identify the factors of 61:
Since 61 is a prime number, its only factors are 1 and 61. -
Check for perfect squares:
A perfect square is a number that can be expressed as the product of an integer with itself. The perfect squares are numbers like 1, 4, 9, 16, etc.
Among the factors of 61, the only perfect square is 1. -
Simplify the radical:
Since the only perfect square factor of 61 is 1, √61 cannot be simplified further. Thus, the exact form remains √61.
In mathematical notation:
\[ \sqrt{61} \approx 7.8102496759067 \]
Here is a quick summary:
- Exact form: √61
- Decimal form: 7.8102496759067
- Exponent form: 611/2
Decimal Representation of √61
The square root of 61 is an irrational number, which means it cannot be expressed as a simple fraction. Instead, it has an infinite number of non-repeating decimal places. The approximate decimal value of √61 is:
\[ \sqrt{61} \approx 7.810249675906654 \]
To simplify calculations, you can round this value to a desired number of decimal places. Commonly, it is rounded to five decimal places:
\[ \sqrt{61} \approx 7.81025 \]
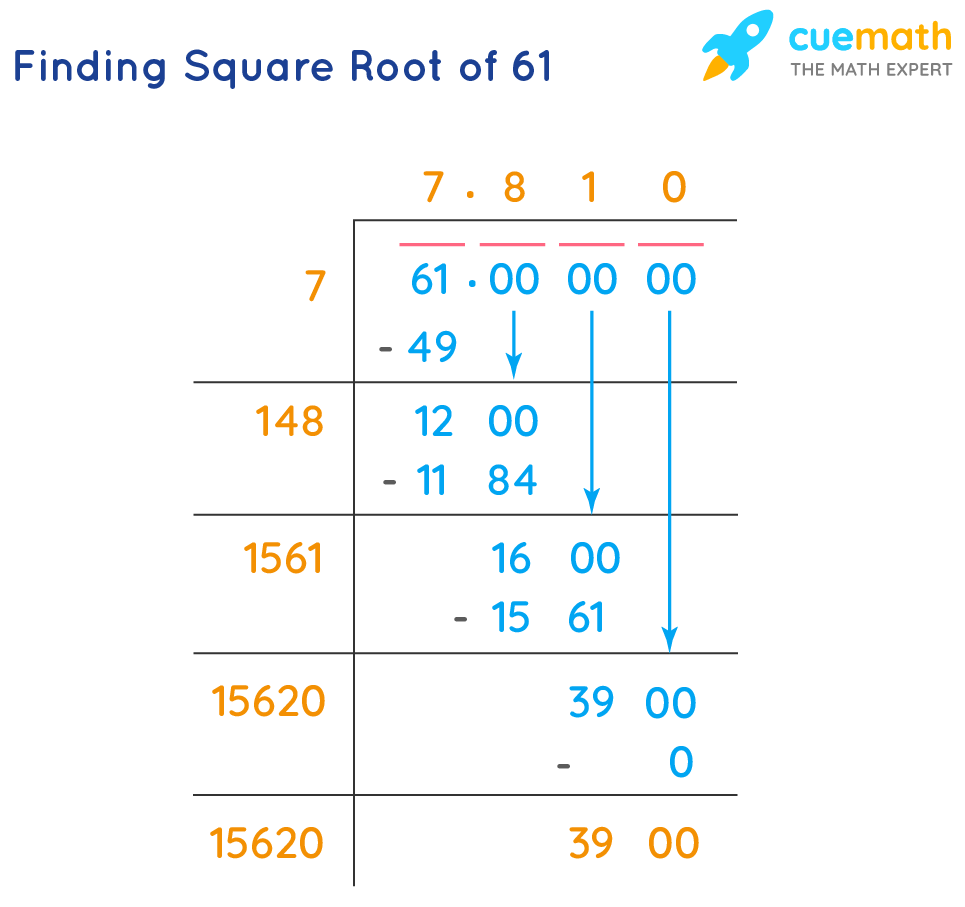
This decimal representation is useful in various applications, such as geometry, physics, and engineering, where precise measurements are crucial. Here is a step-by-step method to calculate the square root of 61 to several decimal places using the long division method:
- Estimate the initial value (7.8 in this case).
- Divide 61 by the estimate (61 ÷ 7.8 ≈ 7.8205).
- Averaging the result with the initial estimate gives a better approximation ((7.8 + 7.8205) / 2 ≈ 7.81025).
- Repeat the process to get more accurate results.
This process can be continued to obtain a more precise value of √61. The more iterations you perform, the closer the approximation will be to the true value.
Exponent Form of √61
The square root of 61 can be represented in different forms. One such form is the exponent form, which is useful in various mathematical contexts.
In exponent form, the square root of 61 is written as:
\[ \sqrt{61} = 61^{\frac{1}{2}} \]
This representation uses the property of exponents that allows us to express a square root as a power of one-half. This form is particularly beneficial when performing algebraic manipulations, such as simplifying expressions or solving equations.
For instance, if we need to multiply the square root of 61 by itself, we can use the exponent form:
\[ \left(61^{\frac{1}{2}}\right)^2 = 61^{\frac{1}{2} \times 2} = 61^1 = 61 \]
This clearly shows that squaring the square root of 61 gives us back the original number, 61. Using the exponent form simplifies the calculation and helps in understanding the properties of square roots.
Here are some steps to convert a square root into its exponent form:
- Identify the number under the square root. In this case, it is 61.
- Write the number as the base of the exponent. For √61, the base is 61.
- Use the exponent of one-half to represent the square root. Thus, √61 becomes 611/2.
Utilizing the exponent form of square roots can make working with these numbers more straightforward in advanced mathematical problems and can be particularly useful in calculus and higher-level algebra.
Steps to Simplify Square Root of 61
Simplifying the square root of 61 involves understanding its properties and the steps to express it in its simplest form. Here are the detailed steps:
- Identify Factors: List the factors of 61. Since 61 is a prime number, its only factors are 1 and 61.
- Check for Perfect Squares: Determine if any of the factors are perfect squares. The only perfect square in the factors of 61 is 1.
- Express in Radical Form: Since there are no perfect square factors other than 1, the simplest radical form of √61 is √61 itself.
Hence, the square root of 61 cannot be simplified further and is already in its simplest form.
| Exact Form | \(\sqrt{61}\) |
| Decimal Form | Approximately 7.81025 |
| Exponent Form | \(61^{\frac{1}{2}}\) |
Prime Factorization Method
Simplifying the square root of 61 using the prime factorization method involves breaking down 61 into its prime factors. Here are the detailed steps:
-
Identify the Prime Factors:
First, we need to find the prime factors of 61. Since 61 is a prime number, it has no other prime factors except 61 itself.
-
Express the Number as a Product of Prime Factors:
Since 61 is already a prime number, it can be expressed as:
\[
61 = 61
\] -
Apply the Square Root to the Prime Factors:
The square root of a product of prime numbers is the product of the square roots of each factor. Therefore, we have:
\[
\sqrt{61} = \sqrt{61}
\] -
Simplify the Expression:
Since 61 has no perfect square factors (other than 1), the square root of 61 cannot be simplified further. Thus, the simplified form remains:
\[
\sqrt{61}
\]
As a result, the square root of 61 in its simplest form is \(\sqrt{61}\). This indicates that 61 does not break down into smaller perfect squares, making it an irreducible radical.
Perfect Squares and Simplification
To simplify a square root, we often look for perfect square factors within the number. A perfect square is a number that is the square of an integer. Here, we will explore how to use perfect squares to simplify square roots.
Unfortunately, the number 61 is a prime number, meaning it does not have any perfect square factors other than 1. This makes the square root of 61 already in its simplest form. However, understanding the process of simplification through perfect squares is crucial for other numbers.
Let's look at some examples where we can simplify square roots using perfect squares:
- Example 1: Simplify √12
- First, factorize 12: 12 = 4 × 3
- Recognize that 4 is a perfect square: √12 = √(4 × 3)
- Apply the square root to the perfect square: √12 = √4 × √3 = 2√3
- So, √12 simplifies to 2√3.
- Example 2: Simplify √45
- First, factorize 45: 45 = 9 × 5
- Recognize that 9 is a perfect square: √45 = √(9 × 5)
- Apply the square root to the perfect square: √45 = √9 × √5 = 3√5
- So, √45 simplifies to 3√5.
- Example 3: Simplify √72
- First, factorize 72: 72 = 36 × 2
- Recognize that 36 is a perfect square: √72 = √(36 × 2)
- Apply the square root to the perfect square: √72 = √36 × √2 = 6√2
- So, √72 simplifies to 6√2.
In conclusion, by identifying and utilizing perfect squares, we can simplify square roots effectively. Although the square root of 61 cannot be simplified further, this method is very useful for other numbers.

Properties of Square Root of 61
The square root of 61 (\(\sqrt{61}\)) has several interesting properties. Below, we explore these properties in detail:
- Irrational Number: The square root of 61 is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal form is non-repeating and non-terminating, approximately equal to 7.810249675906654.
- Exact Form: The exact form of the square root of 61 is \(\sqrt{61}\).
- Decimal Form: When approximated, the square root of 61 is 7.81025 (rounded to five decimal places).
- Exponent Form: In exponent form, the square root of 61 can be written as \(61^{1/2}\).
- Product Property: The square root of a product is the product of the square roots of the factors. For example, \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\). Since 61 is a prime number, this property does not simplify further in this context.
- Sum of Radicals: The sum of \(\sqrt{61}\) with other radicals cannot be simplified unless the radicands are like terms. For example, \(\sqrt{61} + \sqrt{2}\) remains as is.
Let's explore these properties step by step:
- Irrationality: Since 61 is a prime number and not a perfect square, \(\sqrt{61}\) cannot be expressed as a fraction of two integers.
- Exact and Decimal Forms: The exact form is simply \(\sqrt{61}\), and the decimal approximation is useful for practical calculations.
- Exponent Form: Rewriting \(\sqrt{61}\) as \(61^{1/2}\) is helpful in algebraic manipulations and higher mathematics.
- Product Property: For any two numbers \(a\) and \(b\), \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\). However, since 61 is prime, there are no factors other than 1 and 61 itself.
Understanding these properties is crucial in various mathematical applications, from algebra to calculus, and helps in simplifying complex expressions involving radicals.
Square Root of 61 in Various Mathematical Forms
The square root of 61 can be represented in several different mathematical forms. Here are the most common forms:
-
Radical Form: The simplest way to represent the square root of 61 is using the radical sign, which is written as:
$$\sqrt{61}$$
-
Decimal Form: The square root of 61 can also be approximated as a decimal. It is approximately equal to:
$$\sqrt{61} \approx 7.810249675906654$$
This is a non-terminating and non-repeating decimal, indicating that it is an irrational number.
-
Exponential Form: The square root of 61 can be expressed using an exponent. This form is particularly useful in calculus and higher-level mathematics:
$$61^{1/2} \text{ or } 61^{0.5}$$
Understanding these different forms is crucial in various mathematical contexts, such as algebra, geometry, and applied sciences. Each representation has its own applications and advantages, depending on the problem at hand.
Applications of √61 in Real Life
The square root of 61, denoted as \( \sqrt{61} \), can be applied in various real-life scenarios across different fields. Here are some examples:
- Geometry and Design: In architectural design and construction, the square root of non-perfect squares like 61 can be used in calculations involving right triangles, particularly in determining the lengths of diagonals. For instance, if a designer needs to find the diagonal of a rectangle with side lengths that lead to \( \sqrt{61} \) when applying the Pythagorean theorem, it ensures accurate measurements.
- Physics and Engineering: When calculating distances and dimensions, such as the diagonal distance between two points in a coordinate system, \( \sqrt{61} \) might emerge as a critical value. This is crucial in designing components that fit precisely within given spatial constraints.
- Astronomy: In celestial mechanics and calculations involving the orbits of planets or satellites, the square root function is frequently used. Although \( \sqrt{61} \) is not a common exact value, it exemplifies how non-perfect square roots can occur in complex equations that model astronomical phenomena.
- Computer Graphics: In computer graphics and video game design, calculating the distance between points in 2D or 3D space often involves square roots. \( \sqrt{61} \) can represent a distance metric used to render scenes or determine object placements accurately.
- Mathematical Modelling: Square roots are fundamental in solving quadratic equations and optimization problems. In mathematical modelling of real-world problems, \( \sqrt{61} \) might appear in the solutions, reflecting measurements or dimensions that cannot be simplified further.
- Safety and Accident Investigation: In accident reconstruction, the length of skid marks on roads can be analyzed using square roots to estimate the speed of vehicles. Though \( \sqrt{61} \) might not be a typical outcome, understanding square roots' role in these calculations highlights their importance in forensic analysis.
Overall, while \( \sqrt{61} \) might not be the most common square root encountered, it exemplifies the broader application of square roots in various scientific, engineering, and mathematical contexts.
Frequently Asked Questions
-
What is the value of the square root of 61?
The square root of 61 is approximately \( \sqrt{61} \approx 7.81024 \).
-
Why is the square root of 61 an irrational number?
The number 61 is a prime number and does not have any perfect square factors other than 1. Therefore, \( \sqrt{61} \) is an irrational number because it cannot be expressed as a simple fraction.
-
What is the square root of 61 in simplest radical form?
Since 61 is a prime number, it does not have any perfect square factors other than 1. Therefore, the simplest radical form of \( \sqrt{61} \) is \( \sqrt{61} \).
-
If the square root of 61 is 7.81024, what is the value of the square root of 0.61?
The square root of 0.61 can be found by recognizing that \( 0.61 = \frac{61}{100} \). Therefore, \( \sqrt{0.61} = \sqrt{\frac{61}{100}} = \frac{\sqrt{61}}{10} \approx 0.781 \).
-
What is the value of 5 times the square root of 61?
The square root of 61 is approximately 7.81024. Therefore, \( 5 \sqrt{61} = 5 \times 7.81024 \approx 39.0512 \).
-
Is the number 61 a perfect square?
No, 61 is not a perfect square because it is a prime number and cannot be expressed as the product of two equal integers.

Conclusion
Understanding and simplifying the square root of 61 can enhance your mathematical skills and deepen your appreciation for the beauty of numbers. While √61 is not a perfect square and cannot be simplified further into a more concise radical form, recognizing its exact form and various representations is essential.
Here are the key points to remember:
- The square root of 61 is an irrational number, meaning it cannot be expressed as a simple fraction and has an infinite decimal expansion.
- In exact form, the square root of 61 is written as √61.
- The decimal representation of √61 is approximately 7.81025, providing a useful numerical approximation for practical calculations.
- Expressing √61 in exponent form is done by writing it as 610.5.
- Using the prime factorization method for simplification, we find that 61 is a prime number, confirming that √61 cannot be simplified further.
Although the square root of 61 cannot be simplified into a smaller radical, its properties and various forms are valuable in mathematical applications, including solving equations and understanding geometric relationships.
By mastering these concepts, you are better equipped to handle more complex mathematical problems and appreciate the intricacies of irrational numbers. Keep exploring and practicing, and you will continue to develop your mathematical proficiency and confidence.
Tìm hiểu cách đơn giản hóa √(61 + 28√(3)) và √(3.5 + √(10)) trong video hướng dẫn này. Khám phá phương pháp và kỹ thuật để làm chủ số học và các phương trình phức tạp.
Cách Đơn Giản Hóa √(61 + 28√(3)) và √(3.5 + √(10))
READ MORE:
Tìm hiểu cách đơn giản hóa căn bậc hai trong video hướng dẫn này. Khám phá các phương pháp và kỹ thuật để nắm vững số học và giải quyết các phương trình phức tạp.
Cách Đơn Giản Hóa Căn Bậc Hai
















