Topic simplify square root of 42: Unlock the mystery of simplifying the square root of 42 with our comprehensive guide. Discover effective methods, clear steps, and helpful tips to make this mathematical task a breeze. Whether you're a student or a math enthusiast, our guide will help you simplify square roots with confidence and ease. Start mastering square roots today!
Table of Content
- Simplifying the Square Root of 42
- Introduction to Simplifying Square Root of 42
- Understanding Square Roots
- Prime Factorization Method
- Step-by-Step Simplification Process
- Common Mistakes and How to Avoid Them
- Examples of Simplifying Square Root of 42
- Applications in Real Life
- Advanced Techniques for Simplification
- Conclusion and Key Takeaways
- YOUTUBE:
Simplifying the Square Root of 42
The square root of 42, denoted as \( \sqrt{42} \), cannot be simplified further into a simpler radical form because it does not contain any perfect square factors other than 1.
Steps to Simplify
- Identify the prime factors of 42: \( 2, 3, \) and \( 7 \).
- Check for pairs of factors. Since there are no pairs, \( \sqrt{42} \) remains as is.
- Since 1 is the only perfect square factor, \( \sqrt{42} \) is already in its simplest form.
Decimal and Exponent Form
- Decimal Form: \( \sqrt{42} \approx 6.48074 \)
- Exponent Form: \( 42^{1/2} \)
The number 42 is not a perfect square, making its square root an irrational number.
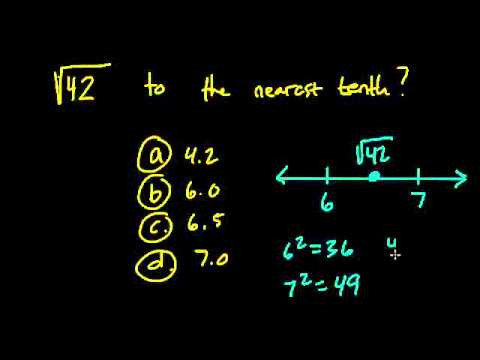
READ MORE:
Introduction to Simplifying Square Root of 42
The square root of 42 is an interesting mathematical expression that can be simplified through various methods. In this section, we'll explore the process of simplifying the square root of 42 step by step, ensuring you understand the concepts and techniques involved. Let's dive into the world of radicals and see how we can make the square root of 42 more manageable.
First, let's recognize that 42 is not a perfect square, which means its square root is an irrational number. However, we can simplify it to a certain extent using prime factorization and other methods. Here’s how:
- Prime Factorization Method:
- Find the prime factors of 42: 42 = 2 × 3 × 7
- Express the square root using these factors: √42 = √(2 × 3 × 7)
- Since there are no repeated prime factors, the square root cannot be simplified further: √42 remains as is.
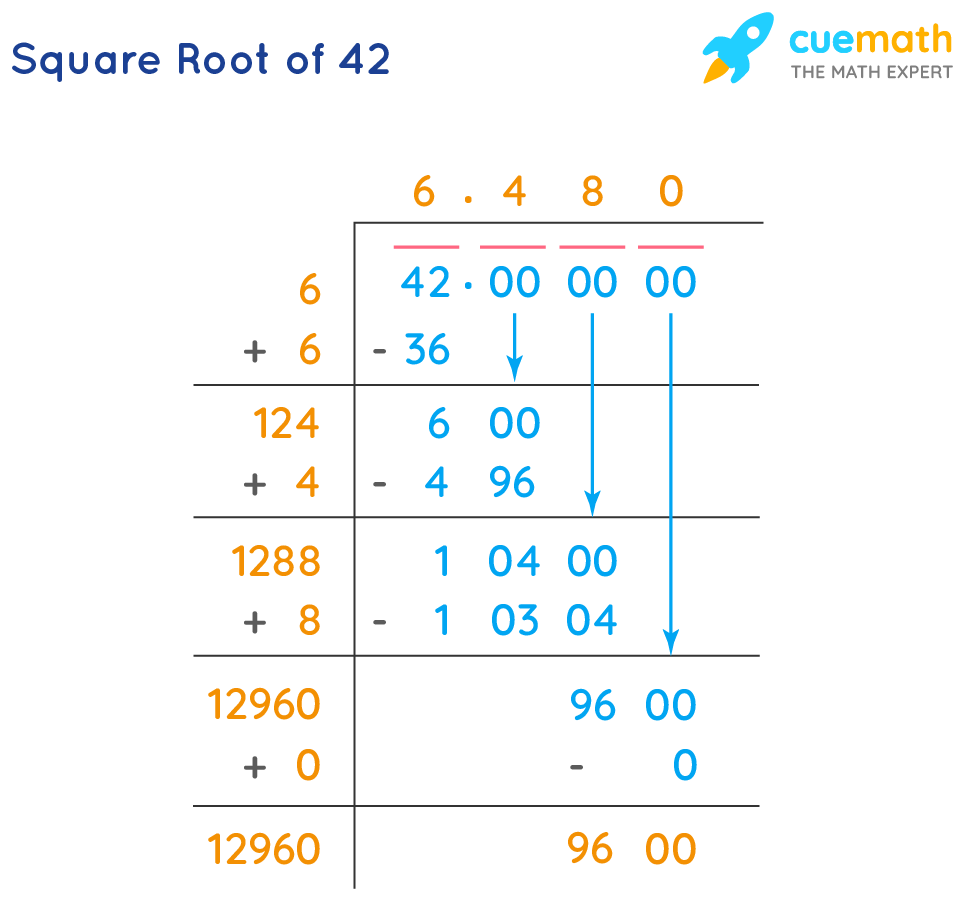
- Long Division Method:
- Write 42 in decimal form with added zeros: 42.000000
- Pair the digits from right to left and find the closest square: 6 × 6 = 36, leaving a remainder of 6
- Double the quotient (6) and use it as part of the new divisor: 12
- Continue the process, bringing down pairs of zeros and finding the appropriate digits to complete the long division, eventually approximating √42 to 6.4807.
By following these methods, we can see that while the square root of 42 can't be simplified into a simpler radical form, we can still approximate its value accurately. Understanding these techniques not only helps in simplifying such expressions but also enhances our overall mathematical problem-solving skills.
Understanding Square Roots
Square roots are mathematical operations that help us find a number which, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because \(4 \times 4 = 16\). Understanding square roots involves recognizing that they are the inverse operation of squaring a number.
To work with square roots effectively, it’s important to understand the following key concepts:
- Radical Sign: The symbol for the square root is \(\sqrt{}\). For instance, \(\sqrt{42}\) denotes the square root of 42.
- Perfect Squares: Numbers like 1, 4, 9, 16, 25, etc., are perfect squares because their square roots are integers.
- Non-Perfect Squares: Numbers like 2, 3, 5, 42, etc., are non-perfect squares. Their square roots are irrational numbers, meaning they cannot be expressed as a simple fraction and have non-repeating decimal expansions.
- Principal Square Root: The principal square root is the non-negative root. For example, \(\sqrt{42}\) refers to the positive root.
To simplify a square root, follow these steps:
- Factorization: Factor the number inside the square root into its prime factors. For instance, 42 can be factored into \(2 \times 3 \times 7\).
- Pairing Factors: Group the prime factors into pairs. Since 42 does not have repeated prime factors, it cannot be simplified further.
- Simplifying the Expression: If there are any pairs of factors, move them outside the square root. For example, \(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\).
Understanding these steps will help you simplify square roots and recognize when they are in their simplest form. In the case of \(\sqrt{42}\), it remains \(\sqrt{42}\) as it cannot be simplified further.
Prime Factorization Method
The prime factorization method is a powerful technique for simplifying square roots by breaking down the number into its prime factors. Let's explore how to simplify the square root of 42 using this method.
- Prime Factorization: Begin by finding the prime factors of 42.
- 42 can be factored into 2, 3, and 7 since \(42 = 2 \times 3 \times 7\).
- Pair the Factors: Identify pairs of prime factors.
- In this case, there are no pairs of prime factors as each factor is unique.
- Simplify: Since there are no pairs, the square root remains in its simplest form.
- The square root of 42 is \(\sqrt{42} = \sqrt{2 \times 3 \times 7}\).
Therefore, \(\sqrt{42}\) cannot be simplified further using the prime factorization method. However, this method helps in understanding the composition of the number and its factors.
Step-by-Step Simplification Process
Simplifying the square root of 42 involves breaking it down into its prime factors and then applying the properties of square roots to simplify further. Here is a detailed step-by-step process to achieve this:
-
Identify the Prime Factors: Begin by finding the prime factors of 42. Since 42 = 2 × 3 × 7, we can express this as:
\[ \sqrt{42} = \sqrt{2 \times 3 \times 7} \]
-
Group the Factors: Next, try to pair the prime factors. However, since 42 does not have any repeated prime factors, we cannot form any perfect squares.
-
Apply the Square Root Property: Use the property of square roots that states:
\[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \]
In this case, we get:
\[ \sqrt{42} = \sqrt{2} \times \sqrt{3} \times \sqrt{7} \]
-
Approximate the Values: Since there are no pairs, the simplest form of \(\sqrt{42}\) is itself. However, for practical purposes, you might approximate the values:
\[ \sqrt{2} \approx 1.414, \quad \sqrt{3} \approx 1.732, \quad \sqrt{7} \approx 2.646 \]
Thus, the approximate value of \(\sqrt{42}\) is:
\[ \sqrt{42} \approx 1.414 \times 1.732 \times 2.646 \approx 6.48 \]
This step-by-step process shows how to simplify and approximate the square root of 42 using prime factorization and basic properties of square roots.
Common Mistakes and How to Avoid Them
Simplifying square roots can be tricky, and it's easy to make mistakes. Here are some common errors and tips on how to avoid them:
- Incorrect Factorization: Ensure you correctly identify the prime factors of the number under the square root. For example, with √42, the prime factors are 2, 3, and 7.
- Forgetting Both Solutions: Remember that when you take the square root of both sides of an equation, you must consider both the positive and negative roots. For instance, √(x^2) = ±x.
- Misapplication of Operations: Always apply the correct mathematical operations in the right order. For example, -x^2 means the square of x is taken first, then the negative sign is applied. Use parentheses if needed to clarify the order, such as (-x)^2.
- Ignoring Properties of Square Roots: Be aware that the square root of a product is not the same as the product of the square roots, i.e., √(a * b) ≠ √a * √b unless both a and b are non-negative.
By keeping these common mistakes in mind and practicing regularly, you can improve your ability to simplify square roots accurately and confidently.
Examples of Simplifying Square Root of 42
Here, we will go through a few examples to illustrate the process of simplifying the square root of 42. By following these step-by-step examples, you will gain a better understanding of how to approach and solve similar problems.
-
Example 1: Simplifying √42 using Prime Factorization
- First, find the prime factors of 42. The prime factors are 2, 3, and 7, so we can write:
\(42 = 2 \times 3 \times 7\) - Next, express the square root of 42 in terms of its prime factors:
\(\sqrt{42} = \sqrt{2 \times 3 \times 7}\) - Since there are no pairs of prime factors, the expression cannot be simplified further. Therefore, the simplest form is:
\(\sqrt{42}\)
- First, find the prime factors of 42. The prime factors are 2, 3, and 7, so we can write:
-
Example 2: Simplifying a Similar Square Root
- Consider the square root of 18. First, find the prime factors:
\(18 = 2 \times 3 \times 3\) - Express the square root in terms of its prime factors:
\(\sqrt{18} = \sqrt{2 \times 3 \times 3}\) - Identify pairs of prime factors. We have a pair of 3s, so we can simplify:
\(\sqrt{18} = \sqrt{3^2 \times 2} = 3\sqrt{2}\)
- Consider the square root of 18. First, find the prime factors:
By comparing these examples, you can see that while the square root of 42 cannot be simplified further, understanding the prime factorization method helps in simplifying other square roots effectively.
Applications in Real Life
Understanding the square root of 42 and how to simplify it has practical applications in various real-life scenarios. Below are some common applications:
-
Architecture and Construction:
Square roots are used to calculate distances, areas, and materials. For instance, if you need to determine the diagonal of a rectangular surface or the height of a triangular structure, simplifying square roots can help in precise measurements.
-
Physics and Engineering:
Square roots are integral in formulas such as those for acceleration, distance, and force. For example, in free-fall calculations, the time it takes for an object to fall from a certain height can be determined using the square root of the height divided by the gravitational constant.
-
Computer Graphics and Gaming:
In graphics, the distance between two points in 2D or 3D space is often calculated using the Pythagorean theorem, which involves square roots. Simplifying these roots can optimize computations and improve performance.
-
Medicine:
Medical professionals use square roots in dosages and measurements. For instance, in radiology, the intensity of radiation exposure decreases with the square of the distance from the source, making understanding and simplifying square roots crucial for safety protocols.
-
Environmental Studies:
Square roots help in determining the growth rate of populations and the spread of pollutants. For instance, calculating the area affected by a pollutant might involve square root calculations.
Advanced Techniques for Simplification
When dealing with more complex square roots, advanced techniques can streamline the simplification process. Here are some methods that can help:
-
Prime Factorization:
Prime factorization involves breaking down the number inside the square root into its prime factors. For instance, to simplify \(\sqrt{42}\), we find that 42 can be factored into 2, 3, and 7.
- \(\sqrt{42} = \sqrt{2 \times 3 \times 7}\)
-
Pairing Factors:
Once factored, look for pairs of identical factors. For every pair, one factor can be taken out of the square root.
- Since there are no pairs in \(\sqrt{42}\), it remains \(\sqrt{42}\).
-
Simplifying Radicals with Variables:
When dealing with variables, apply the same principles of prime factorization and pairing. For example, to simplify \(\sqrt{50x^2}\):
- First, factorize: \(\sqrt{50x^2} = \sqrt{25 \times 2 \times x^2}\).
- Pair and simplify: \(\sqrt{25} \times \sqrt{2} \times \sqrt{x^2} = 5x\sqrt{2}\).
-
Combining Radicals:
If you have multiple radicals, combine them if possible. For example:
- \(\sqrt{50} + \sqrt{2} = \sqrt{25 \times 2} + \sqrt{2} = 5\sqrt{2} + \sqrt{2} = 6\sqrt{2}\).
By using these advanced techniques, you can simplify square roots more efficiently, making complex expressions more manageable.

Conclusion and Key Takeaways
In conclusion, simplifying the square root of 42 involves recognizing that it cannot be simplified into a product of smaller square roots with integer results. This is because 42 does not have any perfect square factors other than 1. Therefore, the simplest form of √42 remains as it is. However, understanding the prime factorization method and the principles of radical simplification are crucial for handling more complex cases.
Here are the key takeaways from our discussion:
- The square root of 42 cannot be simplified further using integer factors.
- The only perfect square factor of 42 is 1, which does not change the radical form.
- Understanding the basics of square roots and prime factorization helps in simplifying other radicals more effectively.
- Simplifying radicals is a fundamental skill in algebra that applies to various mathematical problems and real-life scenarios.
- Practicing with different numbers and their factors enhances your ability to simplify square roots and other radical expressions efficiently.
In practice, whether in algebra, engineering, or daily tasks like determining diagonal measurements, the ability to simplify and understand square roots is valuable. Keep practicing, and you'll find these concepts becoming second nature, making your mathematical journey smoother and more enjoyable.
Cách đơn giản hóa 42 trên 70
READ MORE:
Đơn Giản Hóa 5√42x(4+4√7x)
















