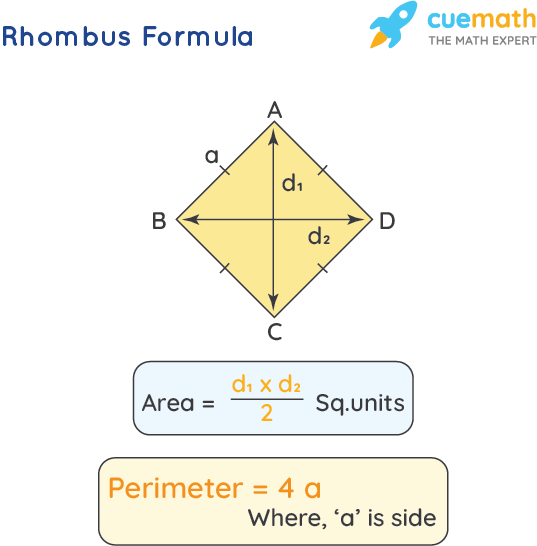
Topic perimeter area and volume: Understanding perimeter, area, and volume is crucial for solving real-world problems in various fields. This article provides essential formulas, practical examples, and tips to master these concepts. Whether you’re a student, teacher, or professional, you'll find valuable insights to enhance your mathematical skills and apply them effectively.
Table of Content
- Perimeter, Area, and Volume
- Introduction to Perimeter, Area, and Volume
- Basic Definitions and Concepts
- Formulas for Common Shapes
- Perimeter Formulas
- Area Formulas
- Volume Formulas
- Application of Perimeter, Area, and Volume in Real Life
- Advanced Topics
- Common Mistakes and Tips for Accuracy
- Interactive Tools and Resources
- Conclusion
- YOUTUBE: Tìm hiểu về chu vi, diện tích và thể tích qua video này với Thầy J. Hướng dẫn chi tiết và dễ hiểu dành cho mọi lứa tuổi.
Perimeter, Area, and Volume
Perimeter
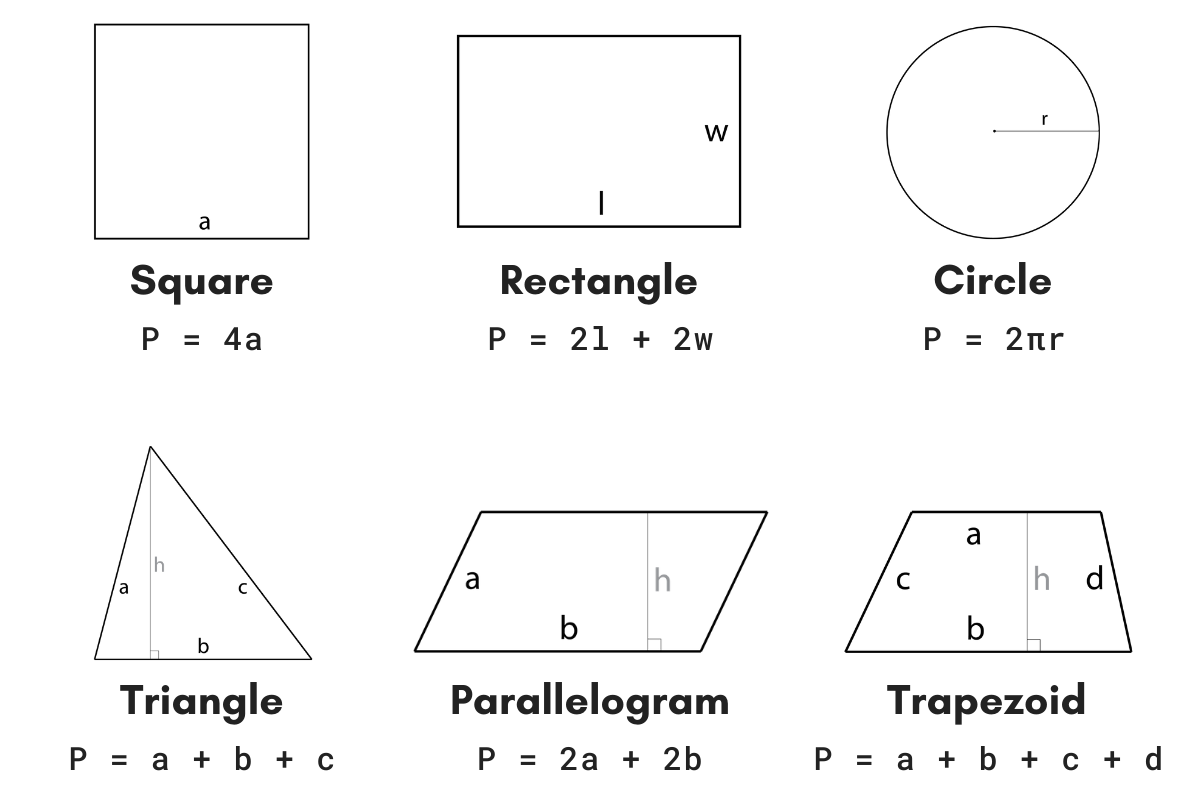
The perimeter is the distance around a two-dimensional shape. It is calculated by adding the lengths of all sides of the shape.
- Rectangle: \( P = 2(l + w) \)
- Square: \( P = 4s \)
- Triangle: \( P = a + b + c \)
- Circle (Circumference): \( C = 2\pi r \)
Area
Area is the measure of the space inside a two-dimensional shape. It is expressed in square units.
- Rectangle: \( A = lw \)
- Square: \( A = s^2 \)
- Triangle: \( A = \frac{1}{2}bh \)
- Circle: \( A = \pi r^2 \)
- Trapezoid: \( A = \frac{1}{2}(a + b)h \)
Volume
Volume is the amount of space inside a three-dimensional object. It is expressed in cubic units.
- Cube: \( V = s^3 \)
- Rectangular Prism: \( V = lwh \)
- Sphere: \( V = \frac{4}{3}\pi r^3 \)
- Cylinder: \( V = \pi r^2h \)
- Cone: \( V = \frac{1}{3}\pi r^2h \)
- Pyramid: \( V = \frac{1}{3}Bh \)
Key Concepts
- Perimeter: Linear measurement of the boundary of a shape.
- Area: Measure of the surface covered by a shape.
- Volume: Measure of the space occupied by an object.

READ MORE:
Introduction to Perimeter, Area, and Volume
Perimeter, area, and volume are fundamental concepts in geometry that measure different aspects of shapes and objects. Understanding these concepts is essential for solving problems in mathematics, physics, engineering, and various other fields.
Perimeter is the total distance around the boundary of a two-dimensional shape. It is calculated by adding the lengths of all the sides. Perimeter is useful in various real-life applications, such as determining the length of fencing required to enclose a garden.
- For a rectangle, the perimeter \( P \) is given by \( P = 2(l + w) \), where \( l \) is the length and \( w \) is the width.
- For a square, the perimeter \( P \) is \( P = 4s \), where \( s \) is the side length.
- For a triangle, the perimeter \( P \) is \( P = a + b + c \), where \( a \), \( b \), and \( c \) are the lengths of the sides.
- For a circle, the perimeter (circumference) \( C \) is \( C = 2\pi r \), where \( r \) is the radius.
Area measures the amount of space inside a two-dimensional shape. It is expressed in square units. Area calculations are essential in fields like architecture, land development, and interior design.
- For a rectangle, the area \( A \) is \( A = lw \), where \( l \) is the length and \( w \) is the width.
- For a square, the area \( A \) is \( A = s^2 \), where \( s \) is the side length.
- For a triangle, the area \( A \) is \( A = \frac{1}{2}bh \), where \( b \) is the base and \( h \) is the height.
- For a circle, the area \( A \) is \( A = \pi r^2 \), where \( r \) is the radius.
- For a trapezoid, the area \( A \) is \( A = \frac{1}{2}(a + b)h \), where \( a \) and \( b \) are the lengths of the parallel sides, and \( h \) is the height.
Volume is the measure of space occupied by a three-dimensional object. It is expressed in cubic units. Volume calculations are crucial in fields such as manufacturing, construction, and fluid dynamics.
- For a cube, the volume \( V \) is \( V = s^3 \), where \( s \) is the side length.
- For a rectangular prism, the volume \( V \) is \( V = lwh \), where \( l \) is the length, \( w \) is the width, and \( h \) is the height.
- For a sphere, the volume \( V \) is \( V = \frac{4}{3}\pi r^3 \), where \( r \) is the radius.
- For a cylinder, the volume \( V \) is \( V = \pi r^2h \), where \( r \) is the radius and \( h \) is the height.
- For a cone, the volume \( V \) is \( V = \frac{1}{3}\pi r^2h \), where \( r \) is the radius and \( h \) is the height.
- For a pyramid, the volume \( V \) is \( V = \frac{1}{3}Bh \), where \( B \) is the area of the base and \( h \) is the height.
By mastering the concepts of perimeter, area, and volume, you can solve a wide range of practical problems, enhance your mathematical skills, and apply these concepts effectively in various disciplines.
Basic Definitions and Concepts
Understanding the concepts of perimeter, area, and volume is fundamental in geometry. These concepts help us measure and describe the properties of various shapes and objects in both two-dimensional (2D) and three-dimensional (3D) spaces.
1. Perimeter
The perimeter of a shape is the total distance around its edges. It's the length of the boundary that encloses a two-dimensional shape. Perimeter is measured in linear units such as meters, centimeters, or feet.
- For a rectangle, the perimeter is calculated as: \( P = 2(l + w) \), where \( l \) is the length and \( w \) is the width.
- For a square, the perimeter is: \( P = 4a \), where \( a \) is the side length.
- For a triangle, the perimeter is the sum of all its sides: \( P = a + b + c \), where \( a \), \( b \), and \( c \) are the lengths of the sides.
- For a circle, the perimeter (also known as the circumference) is: \( C = 2\pi r \), where \( r \) is the radius.
2. Area
The area of a shape is the measure of the space enclosed within its boundary. It is expressed in square units, such as square meters (\( m^2 \)), square centimeters (\( cm^2 \)), or square feet (\( ft^2 \)).
- For a rectangle, the area is: \( A = l \times w \), where \( l \) is the length and \( w \) is the width.
- For a square, the area is: \( A = a^2 \), where \( a \) is the side length.
- For a triangle, the area is: \( A = \frac{1}{2} \times b \times h \), where \( b \) is the base and \( h \) is the height.
- For a circle, the area is: \( A = \pi r^2 \), where \( r \) is the radius.
3. Volume
The volume of a shape measures the amount of space it occupies in three dimensions. It is expressed in cubic units, such as cubic meters (\( m^3 \)), cubic centimeters (\( cm^3 \)), or cubic feet (\( ft^3 \)).
- For a cube, the volume is: \( V = a^3 \), where \( a \) is the side length.
- For a rectangular prism, the volume is: \( V = l \times w \times h \), where \( l \) is the length, \( w \) is the width, and \( h \) is the height.
- For a cylinder, the volume is: \( V = \pi r^2 h \), where \( r \) is the radius and \( h \) is the height.
- For a sphere, the volume is: \( V = \frac{4}{3} \pi r^3 \), where \( r \) is the radius.
4. Units of Measurement
Each of these concepts uses different units of measurement:
- Perimeter is measured in linear units (e.g., meters, feet).
- Area is measured in square units (e.g., square meters, square feet).
- Volume is measured in cubic units (e.g., cubic meters, cubic feet).
5. Understanding the Difference
While perimeter measures the length of the boundary, area measures the space enclosed within that boundary, and volume measures the space occupied by a 3D object. These differences are crucial when solving real-world problems in construction, packaging, and various fields of science and engineering.
Formulas for Common Shapes
In this section, we will explore the formulas for calculating the perimeter, area, and volume of various common shapes. These formulas are essential for solving geometric problems and have practical applications in many fields such as architecture, engineering, and design.
1. Perimeter Formulas
The perimeter is the total length of the boundaries of a two-dimensional shape. Here are the formulas for calculating the perimeter of some common shapes:
- Rectangle
The perimeter \( P \) of a rectangle is given by:
\[ P = 2(l + w) \]where \( l \) is the length and \( w \) is the width.
- Square
The perimeter \( P \) of a square is given by:
\[ P = 4a \]where \( a \) is the side length.
- Triangle
The perimeter \( P \) of a triangle is the sum of its three sides:
\[ P = a + b + c \]where \( a \), \( b \), and \( c \) are the lengths of the sides.
- Circle
The perimeter (or circumference) \( C \) of a circle is given by:
\[ C = 2\pi r \]where \( r \) is the radius.
2. Area Formulas
The area measures the space enclosed within a two-dimensional shape. Below are the formulas for the area of various shapes:
- Rectangle
The area \( A \) of a rectangle is given by:
\[ A = l \times w \]where \( l \) is the length and \( w \) is the width.
- Square
The area \( A \) of a square is given by:
\[ A = a^2 \]where \( a \) is the side length.
- Triangle
The area \( A \) of a triangle is calculated using:
\[ A = \frac{1}{2} \times b \times h \]where \( b \) is the base and \( h \) is the height.
- Circle
The area \( A \) of a circle is given by:
\[ A = \pi r^2 \]where \( r \) is the radius.
- Parallelogram
The area \( A \) of a parallelogram is:
\[ A = b \times h \]where \( b \) is the base and \( h \) is the vertical height.
- Trapezoid
The area \( A \) of a trapezoid is calculated as:
\[ A = \frac{1}{2} \times (b_1 + b_2) \times h \]where \( b_1 \) and \( b_2 \) are the lengths of the two parallel sides and \( h \) is the height.
3. Volume Formulas
Volume measures the amount of space occupied by a three-dimensional object. Here are the formulas for calculating the volume of some common 3D shapes:
- Cube
The volume \( V \) of a cube is given by:
\[ V = a^3 \]where \( a \) is the side length.
- Rectangular Prism
The volume \( V \) of a rectangular prism is:
\[ V = l \times w \times h \]where \( l \) is the length, \( w \) is the width, and \( h \) is the height.
- Cylinder
The volume \( V \) of a cylinder is calculated using:
\[ V = \pi r^2 h \]where \( r \) is the radius of the base and \( h \) is the height.
- Sphere
The volume \( V \) of a sphere is given by:
\[ V = \frac{4}{3} \pi r^3 \]where \( r \) is the radius.
- Cone
The volume \( V \) of a cone is:
\[ V = \frac{1}{3} \pi r^2 h \]where \( r \) is the radius of the base and \( h \) is the height.
Perimeter Formulas
The perimeter of a shape is the total distance around its boundary. It is a linear measurement and is usually expressed in units such as meters, centimeters, or feet. Below, we explore the formulas for calculating the perimeter of various common two-dimensional shapes.
1. Perimeter of a Rectangle
A rectangle has opposite sides of equal length. The perimeter \( P \) of a rectangle is calculated by adding together the lengths of all four sides.
- The formula for the perimeter of a rectangle is:
\[ P = 2(l + w) \]
- where \( l \) is the length and \( w \) is the width.
2. Perimeter of a Square
A square has four equal sides. Therefore, the perimeter \( P \) is simply four times the length of one side.
- The formula for the perimeter of a square is:
\[ P = 4a \]
- where \( a \) is the side length.
3. Perimeter of a Triangle
A triangle has three sides, and the perimeter \( P \) is the sum of the lengths of all its sides.
- The formula for the perimeter of a triangle is:
\[ P = a + b + c \]
- where \( a \), \( b \), and \( c \) are the lengths of the sides.
4. Perimeter of a Circle (Circumference)
The perimeter of a circle is called the circumference \( C \). It is calculated based on the radius \( r \) of the circle.
- The formula for the circumference of a circle is:
\[ C = 2\pi r \]
- where \( r \) is the radius.
5. Perimeter of a Parallelogram
A parallelogram has opposite sides that are equal and parallel. The perimeter \( P \) is the sum of the lengths of all its sides.
- The formula for the perimeter of a parallelogram is:
\[ P = 2(a + b) \]
- where \( a \) and \( b \) are the lengths of the adjacent sides.
6. Perimeter of a Trapezoid
A trapezoid (or trapezium) has a pair of parallel sides of different lengths. The perimeter \( P \) is the sum of the lengths of all four sides.
- The formula for the perimeter of a trapezoid is:
\[ P = a + b + c + d \]
- where \( a \) and \( b \) are the lengths of the parallel sides, and \( c \) and \( d \) are the lengths of the non-parallel sides.
7. Perimeter of a Regular Polygon
A regular polygon has all sides of equal length and all interior angles of equal measure. The perimeter \( P \) is calculated by multiplying the length of one side \( s \) by the total number of sides \( n \).
- The formula for the perimeter of a regular polygon is:
\[ P = n \times s \]
- where \( n \) is the number of sides and \( s \) is the side length.
8. Summary Table of Perimeter Formulas
| Shape | Formula | Variables |
|---|---|---|
| Rectangle | \( P = 2(l + w) \) | \( l \) = length, \( w \) = width |
| Square | \( P = 4a \) | \( a \) = side length |
| Triangle | \( P = a + b + c \) | \( a \), \( b \), \( c \) = side lengths |
| Circle | \( C = 2\pi r \) | \( r \) = radius |
| Parallelogram | \( P = 2(a + b) \) | \( a \) and \( b \) = adjacent side lengths |
| Trapezoid | \( P = a + b + c + d \) | \( a \), \( b \) = parallel side lengths, \( c \), \( d \) = non-parallel side lengths |
| Regular Polygon | \( P = n \times s \) | \( n \) = number of sides, \( s \) = side length |

Area Formulas
Calculating the area of a shape involves determining the amount of space enclosed within its boundaries. Area is typically measured in square units such as square meters (\( m^2 \)), square centimeters (\( cm^2 \)), or square feet (\( ft^2 \)). Below are the formulas for finding the area of various common shapes:
1. Area of a Rectangle
A rectangle has opposite sides that are equal and parallel. The area \( A \) of a rectangle is calculated by multiplying its length by its width.
- The formula for the area of a rectangle is:
\[ A = l \times w \]
- where \( l \) is the length and \( w \) is the width.
2. Area of a Square
A square is a special type of rectangle where all four sides are of equal length. The area \( A \) of a square is the square of the length of its side.
- The formula for the area of a square is:
\[ A = a^2 \]
- where \( a \) is the side length.
3. Area of a Triangle
A triangle has three sides, and its area \( A \) can be calculated using its base and height. The base can be any one of the triangle's sides, and the height is the perpendicular distance from the base to the opposite vertex.
- The formula for the area of a triangle is:
\[ A = \frac{1}{2} \times b \times h \]
- where \( b \) is the base and \( h \) is the height.
4. Area of a Circle
The area \( A \) of a circle is determined by its radius, the distance from the center of the circle to any point on its boundary.
- The formula for the area of a circle is:
\[ A = \pi r^2 \]
- where \( r \) is the radius.
5. Area of a Parallelogram
A parallelogram has opposite sides that are equal and parallel. Its area \( A \) is calculated by multiplying the base by the height, where the height is the perpendicular distance between the bases.
- The formula for the area of a parallelogram is:
\[ A = b \times h \]
- where \( b \) is the base and \( h \) is the height.
6. Area of a Trapezoid
A trapezoid (or trapezium) has a pair of parallel sides of different lengths. The area \( A \) is calculated as the average of the lengths of the two parallel sides multiplied by the height (the perpendicular distance between the parallel sides).
- The formula for the area of a trapezoid is:
\[ A = \frac{1}{2} \times (b_1 + b_2) \times h \]
- where \( b_1 \) and \( b_2 \) are the lengths of the parallel sides, and \( h \) is the height.
7. Area of an Ellipse
An ellipse is a stretched circle and its area \( A \) is determined by its semi-major axis \( a \) and semi-minor axis \( b \).
- The formula for the area of an ellipse is:
\[ A = \pi a b \]
- where \( a \) is the semi-major axis and \( b \) is the semi-minor axis.
8. Summary Table of Area Formulas
| Shape | Formula | Variables |
|---|---|---|
| Rectangle | \( A = l \times w \) | \( l \) = length, \( w \) = width |
| Square | \( A = a^2 \) | \( a \) = side length |
| Triangle | \( A = \frac{1}{2} \times b \times h \) | \( b \) = base, \( h \) = height |
| Circle | \( A = \pi r^2 \) | \( r \) = radius |
| Parallelogram | \( A = b \times h \) | \( b \) = base, \( h \) = height |
| Trapezoid | \( A = \frac{1}{2} \times (b_1 + b_2) \times h \) | \( b_1 \), \( b_2 \) = parallel side lengths, \( h \) = height |
| Ellipse | \( A = \pi a b \) | \( a \) = semi-major axis, \( b \) = semi-minor axis |
Volume Formulas
Volume is a measure of the amount of space occupied by a three-dimensional object. It is usually expressed in cubic units such as cubic meters (\( m^3 \)), cubic centimeters (\( cm^3 \)), or cubic feet (\( ft^3 \)). Below, we provide the formulas for calculating the volume of various common three-dimensional shapes:
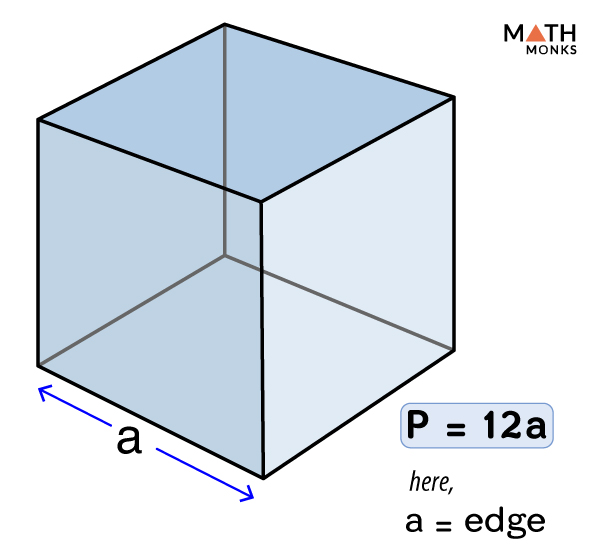
1. Volume of a Cube
A cube is a three-dimensional shape with six equal square faces. The volume \( V \) of a cube is found by cubing the length of one of its sides.
- The formula for the volume of a cube is:
\[ V = a^3 \]
- where \( a \) is the length of a side.
2. Volume of a Rectangular Prism (Cuboid)
A rectangular prism, or cuboid, has six faces that are rectangles. The volume \( V \) is calculated by multiplying its length, width, and height.
- The formula for the volume of a rectangular prism is:
\[ V = l \times w \times h \]
- where \( l \) is the length, \( w \) is the width, and \( h \) is the height.
3. Volume of a Cylinder
A cylinder has two parallel circular bases connected by a curved surface. The volume \( V \) is determined by multiplying the area of the base by the height.
- The formula for the volume of a cylinder is:
\[ V = \pi r^2 h \]
- where \( r \) is the radius of the base and \( h \) is the height.
4. Volume of a Sphere
A sphere is a perfectly round three-dimensional shape. The volume \( V \) of a sphere is calculated using its radius.
- The formula for the volume of a sphere is:
\[ V = \frac{4}{3} \pi r^3 \]
- where \( r \) is the radius.
5. Volume of a Cone
A cone has a circular base and a single vertex not in the plane of the base. The volume \( V \) is one-third the product of the base area and the height.
- The formula for the volume of a cone is:
\[ V = \frac{1}{3} \pi r^2 h \]
- where \( r \) is the radius of the base and \( h \) is the height.
6. Volume of a Pyramid
A pyramid has a polygonal base and triangular faces that converge at a single point. The volume \( V \) is one-third the product of the base area and the height.
- The formula for the volume of a pyramid is:
\[ V = \frac{1}{3} \times B \times h \]
- where \( B \) is the area of the base and \( h \) is the height.
7. Volume of a Ellipsoid
An ellipsoid is a stretched sphere, like a rugby ball. The volume \( V \) is determined by the lengths of its semi-axes.
- The formula for the volume of an ellipsoid is:
\[ V = \frac{4}{3} \pi a b c \]
- where \( a \), \( b \), and \( c \) are the semi-axes.
8. Summary Table of Volume Formulas
| Shape | Formula | Variables |
|---|---|---|
| Cube | \( V = a^3 \) | \( a \) = side length |
| Rectangular Prism | \( V = l \times w \times h \) | \( l \) = length, \( w \) = width, \( h \) = height |
| Cylinder | \( V = \pi r^2 h \) | \( r \) = radius, \( h \) = height |
| Sphere | \( V = \frac{4}{3} \pi r^3 \) | \( r \) = radius |
| Cone | \( V = \frac{1}{3} \pi r^2 h \) | \( r \) = radius, \( h \) = height |
| Pyramid | \( V = \frac{1}{3} \times B \times h \) | \( B \) = base area, \( h \) = height |
| Ellipsoid | \( V = \frac{4}{3} \pi a b c \) | \( a \), \( b \), \( c \) = semi-axes |
Application of Perimeter, Area, and Volume in Real Life
Understanding perimeter, area, and volume is crucial not only in mathematics but also in various real-world applications. These concepts help us to solve practical problems in everyday life, from construction and interior design to packaging and environmental planning. Below are some detailed examples of how perimeter, area, and volume are applied in real-life situations:
1. Perimeter Applications
Perimeter is the total length around a two-dimensional shape. It is widely used in various fields, including:
- Landscaping and Fencing: When designing gardens or outdoor spaces, knowing the perimeter helps in planning the length of fencing needed to enclose an area.
- Sports Fields: The perimeter measurements of sports fields, like soccer or basketball courts, are essential for laying out the boundaries correctly.
- Building Layouts: Architects and builders use perimeter to determine the lengths of walls, which is crucial for material estimation and cost calculations.
2. Area Applications
Area measures the surface covered by a shape. This is essential in various contexts such as:
- Interior Design: Calculating the area of floors, walls, and ceilings is necessary for determining the amount of materials needed, such as paint, tiles, or carpet.
- Agriculture: Farmers use area calculations to plan crop planting, irrigation systems, and land use efficiency.
- Real Estate: Area measurements are crucial in determining the size and value of properties, influencing buying and selling decisions.
- Solar Panel Installation: Engineers need to calculate the area available on rooftops to optimize the number of panels and maximize energy production.
3. Volume Applications
Volume measures the space occupied by a three-dimensional object. It has practical applications in fields like:
- Packaging and Shipping: Determining the volume of containers helps in optimizing space and cost for shipping goods. It is essential for packaging design to ensure products fit well within boxes.
- Construction: Estimating the volume of materials like concrete or soil is necessary for building foundations, pavements, and structures.
- Water Management: Volume calculations are crucial for designing tanks, reservoirs, and swimming pools to manage water storage and distribution effectively.
- Cooking and Baking: Recipes often require volume measurements for ingredients to ensure proper proportions and achieve desired results.
4. Combining Perimeter, Area, and Volume in Design
In many real-life scenarios, these measurements are used together to achieve comprehensive planning and efficient use of resources:
- Urban Planning: Urban planners use area and volume calculations to design cities, taking into account building footprints (area) and the space buildings occupy (volume). Perimeter is used for defining lot boundaries and street layouts.
- Manufacturing: Product designers need to consider the area and volume of parts for efficient material usage and weight management, while perimeter may be relevant for designing the fit and finish of components.
- Environmental Conservation: In environmental studies, calculating the area of habitats and the volume of natural resources like water bodies helps in monitoring and managing ecosystems.
5. Practical Examples
- Painting a Room: To estimate the amount of paint needed, you calculate the area of the walls and ceiling. If you want to install baseboards, you measure the perimeter of the room.
- Filling a Pool: You calculate the volume of the pool to determine how much water is required to fill it and also to estimate the amount of chemicals needed for treatment.
- Buying Flooring: For laying tiles or carpet, you calculate the area of the floor. For edge trims, knowing the perimeter helps in purchasing the right length of materials.
Overall, the concepts of perimeter, area, and volume are essential tools that enhance our ability to plan, design, and solve practical problems in diverse aspects of everyday life.
Advanced Topics
Exploring perimeter, area, and volume further leads us into advanced mathematical concepts and their applications in more complex and specialized fields. These topics extend the basic principles to solve intricate problems in geometry, engineering, physics, and beyond. Here, we delve into some advanced topics that involve these fundamental measurements:
1. Surface Area and Volume of Complex Solids
While basic shapes like cubes and cylinders have straightforward formulas, calculating the surface area and volume of more complex solids requires advanced techniques:
- Composite Shapes: For objects composed of multiple simple shapes, the total volume and surface area are obtained by summing the volumes and surface areas of the individual components.
- Irregular Solids: Methods such as calculus and numerical integration are often used to find the volume and surface area of irregular shapes that do not have simple geometric formulas.
- Frustum of a Cone or Pyramid: The volume \( V \) of a frustum, which is a portion of a cone or pyramid cut by a parallel plane, can be calculated using the formula:
\[ V = \frac{1}{3} \pi h (r_1^2 + r_2^2 + r_1 r_2) \]
- where \( r_1 \) and \( r_2 \) are the radii of the bases, and \( h \) is the height.
2. Application of Calculus in Finding Volume and Surface Area
Calculus provides powerful tools for dealing with complex geometries and variable shapes:
- Volume of Solids of Revolution: When a region is revolved around an axis, the volume of the resulting solid can be determined using integrals. The disk method and shell method are common techniques for such calculations.
- Surface Area of Solids of Revolution: Similar to volume, the surface area of a solid of revolution can be calculated using integrals. The surface area \( S \) of a solid generated by rotating a curve \( y = f(x) \) from \( a \) to \( b \) around the x-axis is given by:
\[ S = 2 \pi \int_a^b f(x) \sqrt{1 + \left( \frac{dy}{dx} \right)^2} \, dx \]
3. Advanced Geometric Applications
Perimeter, area, and volume are used in advanced geometry to solve complex problems:
- Geometric Optimization: Problems that involve maximizing or minimizing a quantity, such as finding the shape with the maximum area for a given perimeter (the isoperimetric problem) or the maximum volume for a given surface area.
- Fractal Geometry: Fractals are complex patterns that exhibit self-similarity at different scales. Calculating the area and volume of fractals often involves special techniques and the concept of fractal dimensions.
4. Real-Life Engineering Applications
Engineers frequently apply advanced concepts of area and volume in their work:
- Structural Engineering: Calculating the volume of materials used in construction and the surface area of structures to assess material costs and strength.
- Fluid Dynamics: Understanding the volume of liquids and gases in different containers and systems is essential for designing pipelines, tanks, and fluid transport systems.
- Aerodynamics: The surface area and volume of aerodynamic shapes like airplane wings and car bodies are crucial for minimizing air resistance and optimizing performance.
5. Advanced Topics in Physics
In physics, volume and surface area are pivotal in understanding and applying various laws:
- Thermodynamics: The surface area and volume of objects affect their heat transfer properties, crucial in designing efficient heating and cooling systems.
- Electromagnetic Theory: The surface area of conductors influences their capacitance and inductance, which are vital in the design of electrical circuits and devices.
6. Mathematical Concepts in Perimeter, Area, and Volume
Advanced mathematical concepts often involve perimeter, area, and volume:
- Vector Calculus: Calculating the flux of a vector field through a surface or the divergence over a volume involves integration over surface areas and volumes.
- Differential Geometry: This branch of mathematics uses concepts of surface area and volume to study curves, surfaces, and their properties.
7. Summary Table of Advanced Formulas
| Concept | Description | Formula |
|---|---|---|
| Frustum Volume | Volume of a frustum of a cone or pyramid | \( V = \frac{1}{3} \pi h (r_1^2 + r_2^2 + r_1 r_2) \) |
| Surface Area of Solids of Revolution | Area of a surface generated by rotating a curve around an axis | \( S = 2 \pi \int_a^b f(x) \sqrt{1 + \left( \frac{dy}{dx} \right)^2} \, dx \) |
By understanding these advanced topics, we can solve more complex and nuanced problems, extending the applications of perimeter, area, and volume into higher dimensions and more sophisticated contexts.

Common Mistakes and Tips for Accuracy
Calculating perimeter, area, and volume can sometimes lead to errors due to misunderstandings or oversight. Below are some common mistakes people make in these calculations and tips to ensure accuracy:
1. Perimeter Calculation Mistakes
- Incorrectly Summing Side Lengths: Ensure all sides of the shape are included in the total length. For instance, forgetting to double the lengths of opposite sides in rectangles or parallelograms.
- Units Mismatch: Always use the same units for all sides before summing. Convert units if necessary to avoid errors.
- Neglecting Curved Segments: When dealing with shapes with curved edges, like circles or semi-circles, include the arc length in the perimeter calculation.
Tip: Double-check your addition and ensure all segments of the boundary are accounted for.
2. Area Calculation Mistakes
- Incorrect Formula Application: Use the correct formula for the shape. For example, applying the area formula for a triangle (\( A = \frac{1}{2} \times \text{base} \times \text{height} \)) to a trapezoid is incorrect.
- Incorrect Dimensions: Verify that the dimensions used are appropriate for the formula. For instance, the height must be perpendicular to the base in triangles and parallelograms.
- Ignoring Unit Conversion: Ensure consistency in units, especially when the given dimensions are in different units. Convert all dimensions to the same unit before calculating the area.
- Overlapping Shapes: When dealing with composite shapes, ensure that areas are added or subtracted correctly to avoid counting overlapping regions multiple times.
Tip: Visualize the shape and confirm the correct formula and dimensions are used. Use unit conversion tables if necessary.
3. Volume Calculation Mistakes
- Misidentifying Shape Type: Different solids have different volume formulas. For example, using the volume formula for a cylinder for a cone will result in errors.
- Incorrect Measurement Units: Volume units are cubic. Make sure all dimensions are converted to the same units before calculating volume.
- Inaccurate Dimension Use: Ensure you are using the correct dimensions for height, radius, or length. For composite shapes, calculate the volume of each part separately before summing.
- Ignoring Pi in Circular Volumes: For shapes like spheres and cylinders, remember to include π (Pi) in your calculations.
Tip: Always identify the shape and corresponding formula. Use consistent units and remember to cube the conversion factor when converting units for volume.
4. General Tips for Accuracy
- Check Your Work: Recalculate and compare results. Cross-check with other methods if possible to verify accuracy.
- Use Diagrams: Drawing a sketch or diagram can help in visualizing the problem and ensuring all parts are accounted for correctly.
- Use Tools and Software: Utilize calculators, software, or apps designed for geometry calculations to reduce manual errors.
- Practice Unit Consistency: Always make sure to use the same units throughout the calculations to avoid errors due to unit mismatch.
- Break Down Complex Shapes: Divide complex shapes into simpler parts, calculate the perimeter, area, or volume of each part, and then sum them appropriately.
5. Examples of Applying Tips for Accuracy
- Composite Shapes: When calculating the area of a shape composed of a rectangle and a semicircle, calculate the area of each separately, ensuring you use π for the semicircle, and then sum them.
- Unit Conversion: For a rectangular prism with dimensions in meters and centimeters, convert all measurements to meters before using the volume formula \( V = l \times w \times h \).
- Use of Software: Geometry software can automatically calculate perimeter, area, and volume, and provide visual verification to reduce the chances of manual errors.
By being aware of these common mistakes and following the tips provided, you can enhance the accuracy of your perimeter, area, and volume calculations, ensuring reliable and precise results in your mathematical and practical applications.
Interactive Tools and Resources
Exploring the concepts of perimeter, area, and volume can be greatly enhanced with interactive tools and resources. These digital aids provide hands-on learning experiences, allowing for dynamic visualization and calculation that simplify complex geometric problems. Here are some of the best interactive tools and resources available online:
1. Online Calculators
Online calculators are invaluable for quickly determining perimeter, area, and volume for various shapes. These tools often include graphical representations to help visualize the calculations.
- Perimeter and Area Calculators: Websites like provide calculators for common shapes, allowing users to input dimensions and instantly get the perimeter and area.
- Volume Calculators: Tools such as the offer calculations for various solids, including cylinders, spheres, and cones, with visual aids for better understanding.
2. Educational Apps and Software
Several apps and software programs offer interactive experiences for learning and practicing geometric concepts:
- GeoGebra: This dynamic mathematics software allows users to create and manipulate geometric shapes to understand properties like perimeter, area, and volume. supports both 2D and 3D visualizations, making it a versatile tool for students and educators.
- Desmos Geometry Tool: provides a user-friendly platform for constructing and exploring geometric figures. It helps in visualizing concepts and performing accurate calculations of perimeter and area.
- Khan Academy: Offering a range of interactive lessons and exercises, covers topics from basic shapes to complex geometric properties, with practice problems and step-by-step solutions.
3. Interactive Tutorials and Videos
Video tutorials and interactive lessons provide a guided learning experience, explaining concepts and demonstrating calculations in an engaging way:
- Math Is Fun: This site offers simple explanations and interactive activities for understanding perimeter, area, and volume. includes practice problems and visual aids to reinforce learning.
- Brightstorm: Brightstorm provides video tutorials that cover a wide range of geometric topics, including detailed explanations and problem-solving strategies for perimeter, area, and volume. Visit for more.
4. Interactive Geometry Tools
These tools offer interactive features for constructing and exploring geometric shapes, aiding in a deeper understanding of their properties:
- Interactive Geometry Editor: Tools like allow users to create and manipulate geometric figures online, calculating properties like perimeter and area dynamically.
- Wolfram Alpha: This powerful computational engine can solve and visualize complex geometric problems. Users can input specific shapes and dimensions to get detailed calculations and visual representations of perimeter, area, and volume. Explore more on .
5. Classroom and Learning Resources
Educational resources and worksheets are excellent for guided practice and learning in classroom settings or for self-study:
- Interactive Worksheets: Websites like provide printable and interactive worksheets on perimeter, area, and volume, offering exercises that range from basic to advanced levels.
- Interactive Math Websites: Platforms like offer interactive practice problems with immediate feedback, covering a wide array of geometric concepts and calculations.
6. Virtual Manipulatives
Virtual manipulatives are digital tools that simulate physical objects, helping users understand geometric concepts through interactive exploration:
- Didax Virtual Manipulatives: provides a variety of online manipulatives, such as rulers, protractors, and geometric shapes, which can be used to explore measurements and properties interactively.
- National Library of Virtual Manipulatives: This resource offers a collection of online tools for visualizing and exploring mathematical concepts, including geometry. Visit the for interactive activities on perimeter, area, and volume.
Utilizing these interactive tools and resources can significantly enhance your understanding and application of perimeter, area, and volume. Whether for educational purposes, professional use, or personal interest, these tools provide valuable assistance in mastering these essential mathematical concepts.
Conclusion
Understanding the concepts of perimeter, area, and volume is essential for solving various problems in geometry and real life. These measurements allow us to quantify the space within different shapes and objects, aiding in everything from architectural design to everyday tasks.
In summary, here are the key takeaways:
- Perimeter: The distance around a two-dimensional shape. Calculated by summing the lengths of all sides.
- Area: The amount of space within a two-dimensional shape. Calculated using specific formulas for different shapes.
- Volume: The amount of space within a three-dimensional object. Calculated using formulas that account for the object's dimensions.
By mastering these concepts, you can:
- Enhance your problem-solving skills in mathematics and geometry.
- Apply these measurements to real-life situations, such as construction, landscaping, and interior design.
- Avoid common mistakes by double-checking calculations and understanding the properties of shapes and objects.
For those looking to delve deeper into these topics, consider exploring the following advanced topics:
- Calculating the surface area and volume of more complex shapes like pyramids, cylinders, and spheres.
- Understanding the principles of calculus as they apply to area and volume.
- Utilizing computer software and interactive tools to model and solve geometric problems.
In conclusion, the study of perimeter, area, and volume provides a foundational understanding of geometry that is both practical and applicable in various fields. Continued practice and application will lead to greater accuracy and confidence in using these essential mathematical concepts.
Thank you for exploring this comprehensive guide. We hope it has been informative and helpful in enhancing your understanding of perimeter, area, and volume.
Tìm hiểu về chu vi, diện tích và thể tích qua video này với Thầy J. Hướng dẫn chi tiết và dễ hiểu dành cho mọi lứa tuổi.
Chu vi, Diện tích và Thể tích Giải thích | Toán học với Thầy J
READ MORE:
Khám phá những điều cơ bản về chu vi và diện tích qua video này từ Khan Academy. Hướng dẫn chi tiết và dễ hiểu cho học sinh mọi lứa tuổi.
Chu vi và diện tích: những điều cơ bản | Chu vi, diện tích và thể tích | Hình học | Khan Academy