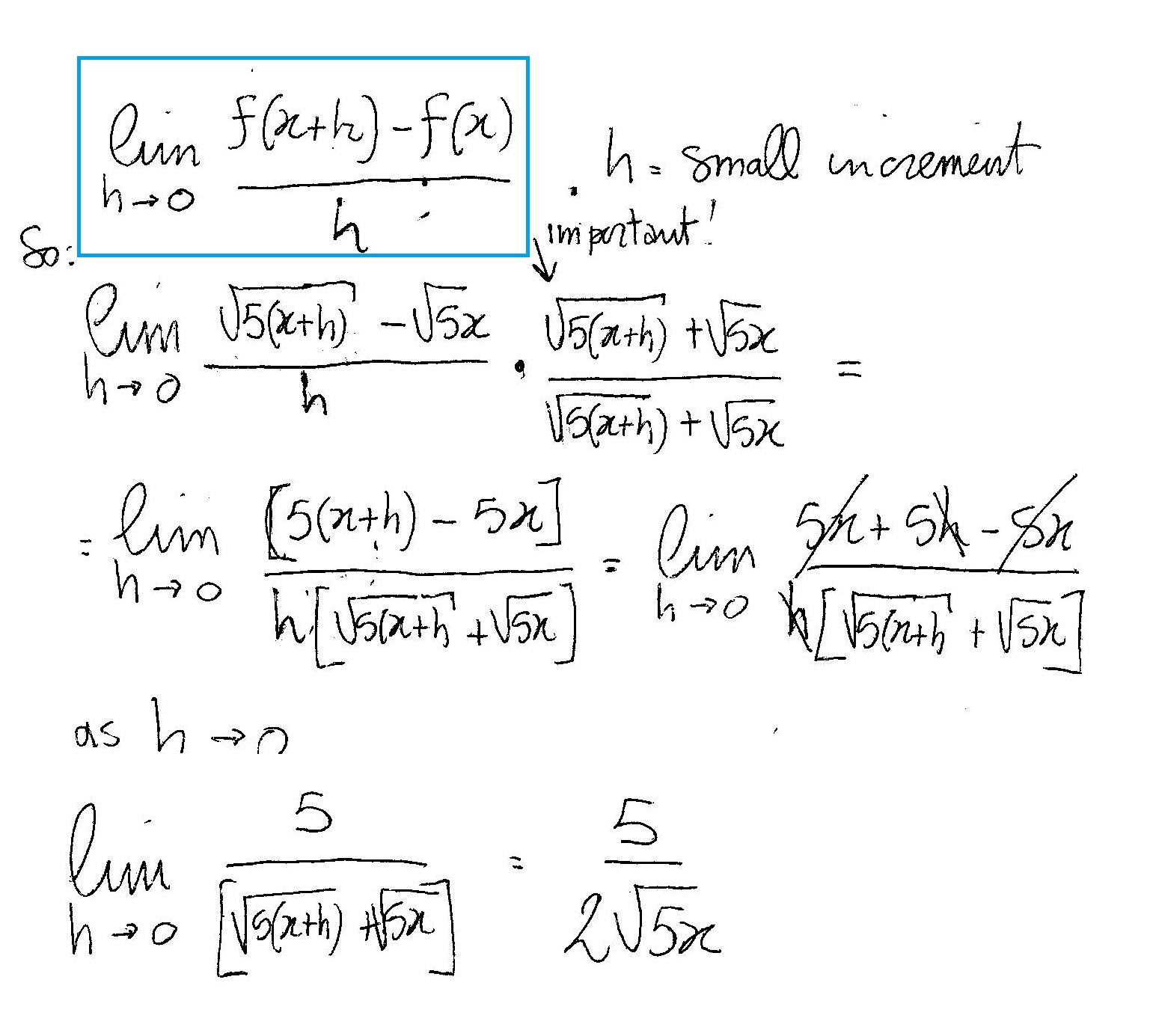
Topic 5 square root x: Explore the fascinating world of the expression \(5\sqrt{x}\). This article delves into its mathematical properties, graphing techniques, and practical applications. Whether you're a student or a math enthusiast, you'll find valuable insights and step-by-step guides to master this concept. Join us on a journey to unlock the secrets of \(5\sqrt{x}\)!
Table of Content
- Understanding the Expression: \(5\sqrt{x}\)
- Introduction to 5 Square Root x
- Mathematical Definition and Properties
- Graphing the Function y = 5√x
- Step-by-Step Guide to Plotting the Graph
- Domain and Range of 5√x
- Applications in Various Fields
- Example Problems and Solutions
- Common Mistakes and How to Avoid Them
- Advanced Topics Involving 5√x
- Practice Exercises
- Conclusion and Summary
- YOUTUBE: Video hướng dẫn đơn giản hóa biểu thức căn bậc hai của x^5. Tìm hiểu cách làm một cách dễ hiểu và chính xác.
Understanding the Expression: \(5\sqrt{x}\)
The mathematical expression \(5\sqrt{x}\) represents the function where 5 is multiplied by the square root of \(x\). This expression is commonly encountered in algebra and various applications involving roots and exponents.
Key Features of the Expression \(5\sqrt{x}\)
- The term \( \sqrt{x} \) denotes the principal square root of \(x\).
- The coefficient 5 scales the value of the square root.
Graphing \(y = 5\sqrt{x}\)
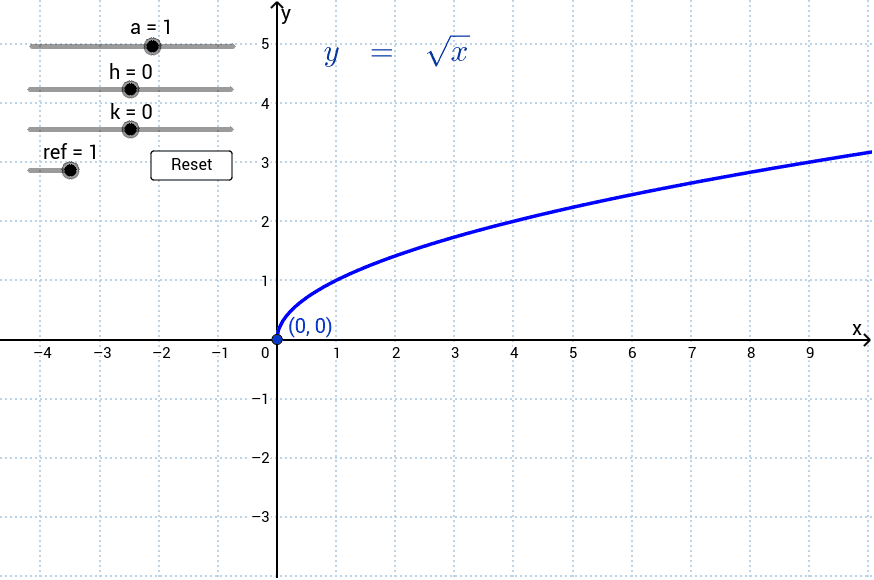
The graph of the function \(y = 5\sqrt{x}\) is a transformation of the basic square root function \(y = \sqrt{x}\), scaled vertically by a factor of 5.
Steps to Graph \(y = 5\sqrt{x}\)
- Identify the domain: The expression under the square root, \(x\), must be non-negative. Therefore, \(x \geq 0\).
- Calculate key points: Select values of \(x\) and compute corresponding \(y\) values.
- For \(x = 0\), \(y = 5\sqrt{0} = 0\).
- For \(x = 1\), \(y = 5\sqrt{1} = 5\).
- For \(x = 4\), \(y = 5\sqrt{4} = 10\).
- For \(x = 9\), \(y = 5\sqrt{9} = 15\).
- Plot the points and draw a smooth curve through them.
Applications of \(5\sqrt{x}\)
The function \(5\sqrt{x}\) is used in various fields including physics, engineering, and finance to model phenomena where growth rates are proportional to the square root of a variable.
Example Problems
Here are some examples to illustrate the use of \(5\sqrt{x}\):
| Problem | Solution |
|---|---|
| Evaluate \(5\sqrt{16}\) | \(5 \times 4 = 20\) |
| Find the value of \(x\) when \(5\sqrt{x} = 25\) | Solve \( \sqrt{x} = 5 \) => \( x = 25 \) |
READ MORE:
Introduction to 5 Square Root x
The expression \(5 \sqrt{x}\) involves finding the square root of a variable \(x\) and then multiplying the result by 5. This concept is fundamental in algebra and is commonly encountered in various mathematical problems and applications. Understanding how to work with square roots is essential for simplifying expressions, solving equations, and analyzing functions.
Square roots are operations that find a number which, when multiplied by itself, gives the original number under the radical sign. For example, the square root of 25 is 5, because \(5 \times 5 = 25\). In the context of \(5 \sqrt{x}\), if \(x\) is a perfect square, the calculation is straightforward. If not, it might be left in simplified radical form.
Here are some important points to consider when working with \(5 \sqrt{x}\):
- For \(x \ge 0\), the square root function produces real numbers. If \(x < 0\), the result involves imaginary numbers.
- The principal square root is the non-negative root of \(x\).
- Simplifying square roots involves breaking down \(x\) into its prime factors and identifying perfect squares.
For example, to simplify \(5 \sqrt{45}\):
- Factorize 45 to \(9 \times 5\).
- Recognize that 9 is a perfect square (32).
- Rewrite the expression: \(5 \sqrt{45} = 5 \sqrt{9 \times 5} = 5 \times 3 \sqrt{5} = 15 \sqrt{5}\).
Understanding and manipulating expressions like \(5 \sqrt{x}\) are essential skills in mathematics, enabling you to solve a wide range of problems efficiently.
Mathematical Definition and Properties
The expression \(5\sqrt{x}\) combines a constant multiplier with the square root of a variable, x. The square root function, denoted as \(\sqrt{x}\), is defined as the value that, when multiplied by itself, gives the original number \(x\). The mathematical properties and steps involved in understanding \(5\sqrt{x}\) are outlined below:
- Square Root Definition: The square root of a number \(x\) is a value \(r\) such that \(r^2 = x\). The principal square root is the non-negative root, represented as \(\sqrt{x}\).
- Multiplication Property: When a constant is multiplied by a square root, it can be written as \(a\sqrt{b}\), where \(a\) is the constant and \(b\) is the number or expression inside the square root.
- Example Calculation: For \(5\sqrt{x}\), if \(x = 16\), then \(5\sqrt{16} = 5 \times 4 = 20\).
- Simplification: If \(x\) can be factored into a perfect square, \(\sqrt{x}\) can be simplified. For example, \(\sqrt{36} = 6\), so \(5\sqrt{36} = 5 \times 6 = 30\).
Square roots have unique properties that are useful in algebra and other mathematical fields. Understanding these properties allows for simplification and better manipulation of expressions involving square roots.
Graphing the Function y = 5√x
The function \( y = 5\sqrt{x} \) represents a transformed version of the parent square root function \( y = \sqrt{x} \). This function is scaled vertically by a factor of 5. Here is a step-by-step guide to graphing this function:
-
Determine the Domain: The square root function is defined for all \( x \geq 0 \). Therefore, the domain of \( y = 5\sqrt{x} \) is \( [0, \infty) \).
-
Identify Key Points: To plot the graph accurately, choose a few values of \( x \) and compute the corresponding \( y \) values.
x 0 1 4 9 16 y 0 5 10 15 20 -
Plot the Points: Using the key points from the table, plot them on a coordinate plane. The points are (0, 0), (1, 5), (4, 10), (9, 15), and (16, 20).
-
Draw the Curve: Connect the points with a smooth curve, starting from (0, 0) and moving rightward and upward, reflecting the increasing nature of the function.
-
Analyze the Graph: The graph of \( y = 5\sqrt{x} \) will be a continuous curve starting from the origin and extending infinitely to the right. The function increases at a decreasing rate.
This step-by-step method ensures a clear understanding of how to graph the function \( y = 5\sqrt{x} \). Remember that the vertical stretch by a factor of 5 makes the graph steeper compared to the parent function \( y = \sqrt{x} \).
Step-by-Step Guide to Plotting the Graph
To plot the graph of the function \( y = 5\sqrt{x} \), follow these detailed steps:
- Understand the Function:
The function \( y = 5\sqrt{x} \) is a square root function scaled by a factor of 5. It represents the square root of \( x \) multiplied by 5.
- Determine the Domain:
The domain of \( y = 5\sqrt{x} \) includes all non-negative real numbers, as the square root function is not defined for negative values. Thus, \( x \geq 0 \).
- Create a Table of Values:
Choose values of \( x \) within the domain and calculate the corresponding \( y \) values.
x y = 5√x 0 0 1 5 4 10 9 15 16 20 - Plot the Points:
On a graph paper or using graphing software, plot the points from the table: (0,0), (1,5), (4,10), (9,15), and (16,20).
- Draw the Curve:
Connect the plotted points with a smooth curve. Since the function \( y = 5\sqrt{x} \) is continuous for all \( x \geq 0 \), the graph will be a smooth curve starting from the origin (0,0) and extending to the right.
- Analyze the Graph:
- Shape: The graph is a half-parabola opening to the right.
- Behavior: As \( x \) increases, \( y \) increases. The rate of increase of \( y \) slows down as \( x \) becomes larger.
- Intercepts: The graph intersects the y-axis at the origin (0,0).
- Range: The range of the function is all non-negative real numbers (\( y \geq 0 \)).
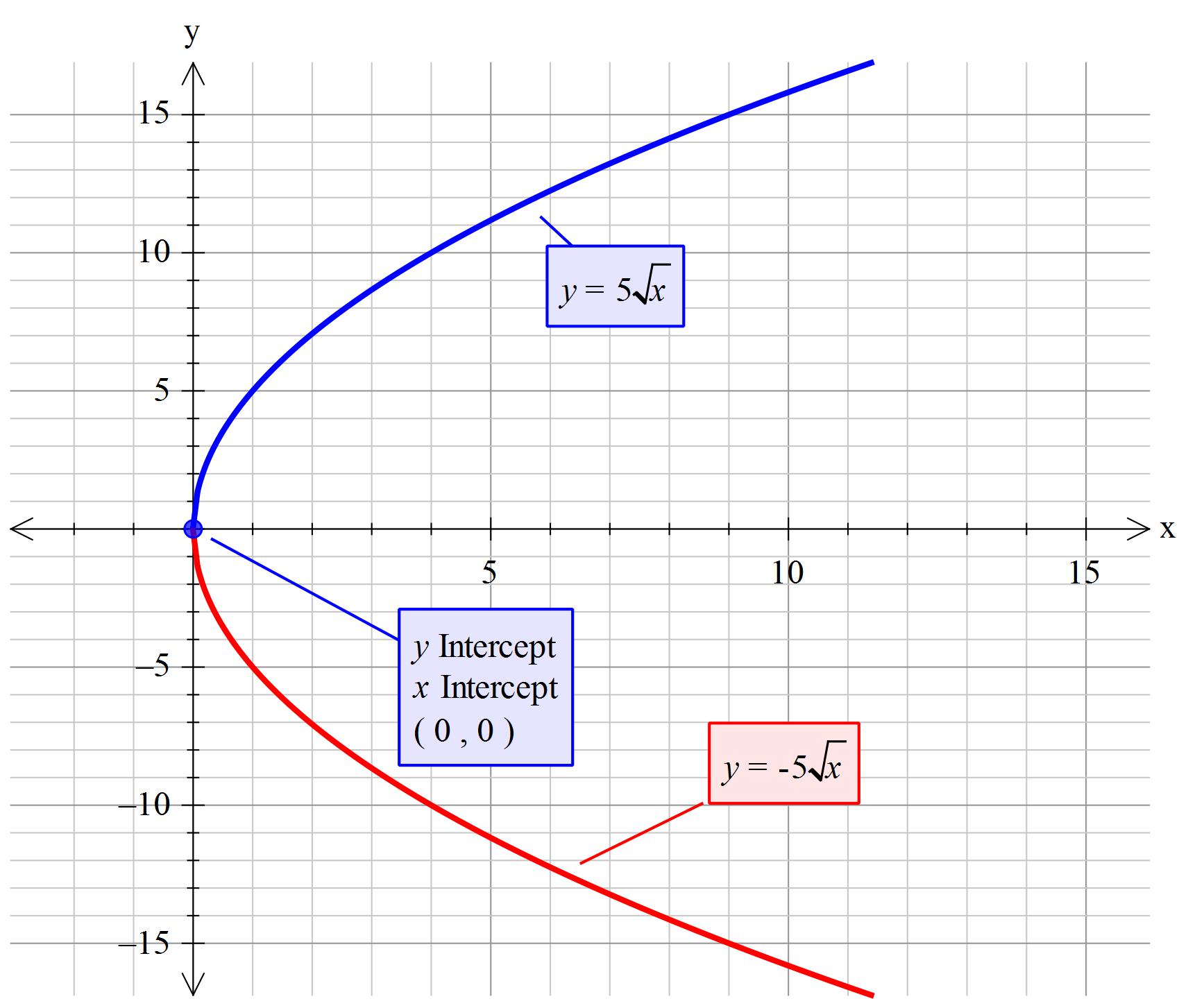
Domain and Range of 5√x
The domain of the function \( y = 5\sqrt{x} \) includes all non-negative real numbers since the square root function \( \sqrt{x} \) is defined for \( x \geq 0 \). Therefore, the domain is \( [0, \infty) \).
For the range of \( y = 5\sqrt{x} \), consider that as \( x \) increases from 0 to \( \infty \), \( \sqrt{x} \) also increases from 0 to \( \infty \). Multiplying \( \sqrt{x} \) by 5 stretches these values vertically. Thus, the range of \( y \) is \( [0, \infty) \).
Applications in Various Fields
The function \( y = 5\sqrt{x} \) finds applications in several fields:
- Engineering: Used in designing curved surfaces and calculating distances in quadratic optimization problems.
- Physics: Describes the motion of particles under certain forces where the distance varies as the square root of time or distance.
- Finance: Models exponential growth scenarios where investments or savings grow over time at a proportional rate.
- Biology: Models population growth in limited resources environments where growth rates are proportional to the square root of available resources.
- Computer Science: Utilized in algorithms for optimization and heuristic searches where the square root function helps balance exploration and exploitation.
Example Problems and Solutions
Here are some example problems and their solutions involving the function \( y = 5\sqrt{x} \):
- Problem 1: Find \( y \) when \( x = 9 \).
- Problem 2: Determine the domain of the function \( y = 5\sqrt{x} \).
- Problem 3: Find the range of \( y = 5\sqrt{x} \).
| Solution: | \( y = 5\sqrt{9} = 5 \times 3 = 15 \). |
| Solution: | The domain is \( [0, \infty) \) because \( \sqrt{x} \) is defined for \( x \geq 0 \). |
| Solution: | The range is \( [0, \infty) \) because as \( x \) increases from 0 to \( \infty \), \( \sqrt{x} \) also increases, and multiplying by 5 stretches these values vertically. |
Common Mistakes and How to Avoid Them
When working with the expression \(5\sqrt{x}\), students often encounter several common mistakes. Understanding these errors and learning how to avoid them is crucial for mastering this mathematical concept.
- Incorrectly Simplifying Square Roots: One common mistake is incorrectly simplifying expressions involving square roots. For example, students may incorrectly write \(\sqrt{25} = \pm 5\). The correct simplification is \(\sqrt{25} = 5\) because the principal square root is always non-negative.
Correct Method: Ensure that you always take the positive root when simplifying square roots. For instance, \(\sqrt{36} = 6\), not \(\pm 6\).
- Misunderstanding the Domain: Another frequent error is misunderstanding the domain of the function \(5\sqrt{x}\). Students may attempt to use negative values for \(x\), which are not in the domain of the square root function.
Correct Method: Remember that the domain of \(5\sqrt{x}\) is \(x \geq 0\). Always ensure that \(x\) is non-negative to avoid taking the square root of a negative number, which is undefined in the set of real numbers.
- Confusing the Order of Operations: Errors often occur when students do not correctly follow the order of operations, especially in expressions involving multiplication and square roots. For example, they might incorrectly calculate \(5\sqrt{4 + 1}\) as \(5 \cdot \sqrt{4} + \sqrt{1}\).
Correct Method: Follow the correct order of operations: first, simplify inside the square root, then take the square root, and finally multiply by 5. So, \(5\sqrt{4 + 1} = 5\sqrt{5}\).
- Forgetting the Absolute Value: When simplifying expressions such as \(\sqrt{x^2}\), students may forget that the result should be the absolute value of \(x\), not just \(x\).
Correct Method: Always include the absolute value when simplifying the square root of a squared term. For example, \(\sqrt{x^2} = |x|\), not simply \(x\).
- Misinterpreting Graph Behavior: Students often misinterpret the behavior of the graph of \(5\sqrt{x}\), especially its starting point and direction. They might think the graph extends into the negative \(x\) values or starts at a point other than \((0, 0)\).
Correct Method: The graph of \(5\sqrt{x}\) starts at the origin (0,0) and only exists for \(x \geq 0\). Ensure that you understand the basic shape and direction of the graph, which increases slowly and steadily as \(x\) increases.
By being aware of these common mistakes and practicing correct methods, students can improve their understanding and accuracy when working with the function \(5\sqrt{x}\).

Advanced Topics Involving 5√x
In this section, we will explore some advanced mathematical concepts involving the function \(5\sqrt{x}\). These topics include the differentiation and integration of the function, transformations, and solving equations involving \(5\sqrt{x}\).
1. Differentiation of \(5\sqrt{x}\)
To find the derivative of \(5\sqrt{x}\), we will use the chain rule. The function can be rewritten as \(5x^{1/2}\). The chain rule states that if you have a function \(f(g(x))\), its derivative is \(f'(g(x)) \cdot g'(x)\).
For \(5x^{1/2}\), let \(u = x^{1/2}\). Then the derivative of \(5u\) is \(5 \cdot \frac{d}{dx}(u)\).
Since \(u = x^{1/2}\), the derivative of \(u\) with respect to \(x\) is \(\frac{1}{2}x^{-1/2}\).
Combining these results:
\[
\frac{d}{dx}[5\sqrt{x}] = 5 \cdot \frac{1}{2}x^{-1/2} = \frac{5}{2}x^{-1/2} = \frac{5}{2\sqrt{x}}
\]
2. Integration of \(5\sqrt{x}\)
To integrate \(5\sqrt{x}\), we use the reverse of the power rule. The integral of \(x^n\) is \(\frac{x^{n+1}}{n+1}\) for any \(n \neq -1\).
Rewriting \(5\sqrt{x}\) as \(5x^{1/2}\), we find:
\[
\int 5\sqrt{x} \, dx = \int 5x^{1/2} \, dx = 5 \cdot \frac{x^{3/2}}{3/2} = \frac{10}{3}x^{3/2} + C
\]
3. Transformations Involving \(5\sqrt{x}\)
Transformations can shift, stretch, or reflect the graph of \(5\sqrt{x}\). Consider the general form \(a\sqrt{bx - c} + d\):
- Vertical Stretch/Compression: Multiplying the function by \(a\) stretches (if \(|a| > 1\)) or compresses (if \(|a| < 1\)) the graph vertically.
- Horizontal Stretch/Compression: The coefficient \(b\) inside the square root affects horizontal stretching or compressing. If \(b > 1\), the graph compresses horizontally; if \(0 < b < 1\), it stretches.
- Horizontal Shift: The term \(c\) inside the square root shifts the graph horizontally. If \(c > 0\), the graph shifts to the right; if \(c < 0\), it shifts to the left.
- Vertical Shift: The term \(d\) outside the square root shifts the graph vertically. If \(d > 0\), the graph shifts up; if \(d < 0\), it shifts down.
4. Solving Equations Involving \(5\sqrt{x}\)
Consider the equation \(5\sqrt{x} = k\), where \(k\) is a constant. To solve for \(x\), follow these steps:
- Isolate the square root: \(\sqrt{x} = \frac{k}{5}\).
- Square both sides to eliminate the square root: \(x = \left(\frac{k}{5}\right)^2\).
- Simplify the expression: \(x = \frac{k^2}{25}\).
5. Example Problem
Let's solve the equation \(5\sqrt{x} = 20\):
- Isolate the square root: \(\sqrt{x} = \frac{20}{5} = 4\).
- Square both sides: \(x = 4^2 = 16\).
- Solution: \(x = 16\).
6. Chain Rule Application
For a more complex function, say \(5\sqrt{3x^2 - x}\), we use the chain rule. Let \(u = 3x^2 - x\), then the function is \(5\sqrt{u}\). The derivative is:
\[
\frac{d}{dx}[5\sqrt{3x^2 - x}] = 5 \cdot \frac{1}{2}(3x^2 - x)^{-1/2} \cdot (6x - 1)
\]
Simplifying, we get:
\[
\frac{d}{dx}[5\sqrt{3x^2 - x}] = \frac{5(6x - 1)}{2\sqrt{3x^2 - x}}
\]
These advanced topics provide a deeper understanding of the function \(5\sqrt{x}\) and its applications. Mastery of these concepts is essential for higher-level mathematics and various applications in science and engineering.
Practice Exercises
Below are a set of practice exercises designed to help you understand and master the function \(5\sqrt{x}\). These exercises cover various aspects of the function including simplification, evaluation, and application in equations.
-
Simplify the following expressions:
- \(\sqrt{25x^2}\)
- \(\sqrt{180x^3}\)
- \(\sqrt{64r^2s^6t^5}\)
- \(\sqrt{144r^8s^6t^2}\)
-
Evaluate \(5\sqrt{x}\) for the following values of \(x\):
- \(x = 1\)
- \(x = 4\)
- \(x = 9\)
- \\(x = 16\)
-
Solve the following equations for \(x\):
- \(5\sqrt{x} = 10\)
- \(5\sqrt{x} = 15\)
- \(5\sqrt{x} = 20\)
- \(5\sqrt{x} = 25\)
-
Simplify and rationalize the denominators:
- \(\sqrt{\frac{9x^3}{25y^2}}\)
- \(\sqrt{\frac{4x^5}{9y^4}}\)
- \(\sqrt{\frac{m^7}{36n^4}}\)
- \(\sqrt{\frac{147m^9}{n^6}}\)
Answers:
-
- \(\sqrt{25x^2} = 5x\)
- \(\sqrt{180x^3} = 6x\sqrt{5x}\)
- \(\sqrt{64r^2s^6t^5} = 8rs^3t^2\sqrt{t}\)
- \(\sqrt{144r^8s^6t^2} = 12r^4s^3t\)
-
- \(5\sqrt{1} = 5\)
- \(5\sqrt{4} = 10\)
- \(5\sqrt{9} = 15\)
- \(5\sqrt{16} = 20\)
-
- \(5\sqrt{x} = 10 \implies \sqrt{x} = 2 \implies x = 4\)
- \(5\sqrt{x} = 15 \implies \sqrt{x} = 3 \implies x = 9\)
- \(5\sqrt{x} = 20 \implies \sqrt{x} = 4 \implies x = 16\)
- \(5\sqrt{x} = 25 \implies \sqrt{x} = 5 \implies x = 25\)
-
- \(\sqrt{\frac{9x^3}{25y^2}} = \frac{3x\sqrt{x}}{5y}\)
- \(\sqrt{\frac{4x^5}{9y^4}} = \frac{2x^2\sqrt{x}}{3y^2}\)
- \(\sqrt{\frac{m^7}{36n^4}} = \frac{m^{7/2}}{6n^2}\)
- \(\sqrt{\frac{147m^9}{n^6}} = \frac{3\sqrt{7}m^{9/2}}{n^3}\)
Conclusion and Summary
In this guide, we have thoroughly explored the expression \(5 \sqrt{x}\) from its basic definition to advanced applications. Understanding the function \( y = 5 \sqrt{x} \) involves grasping its properties, graphing techniques, domain and range, and real-world applications.
Key takeaways include:
- Definition: The expression \(5 \sqrt{x}\) represents a function where each input \(x\) is transformed by taking the square root and then multiplying by 5.
- Graphing: The graph of \( y = 5 \sqrt{x} \) is a half-parabola opening upwards, starting from the origin. It is crucial to understand how to plot this graph by selecting appropriate values of \(x\) and calculating the corresponding \(y\)-values.
- Domain and Range: The domain of \( y = 5 \sqrt{x} \) is \( x \geq 0 \), as square roots of negative numbers are not real. The range is \( y \geq 0 \).
- Applications: This function appears in various fields such as physics, engineering, and finance, often in scenarios involving rates of change and growth models.
- Example Problems: We provided several example problems with detailed solutions to illustrate the application of the function in different contexts.
- Common Mistakes: Common errors include misinterpreting the domain and range, incorrect graph plotting, and algebraic mistakes in manipulating the square root.
- Advanced Topics: We discussed higher-level applications and transformations of the function, including compositions with other functions and solving equations involving \(5 \sqrt{x}\).
By mastering these aspects, one can confidently work with the expression \(5 \sqrt{x}\) and apply it in both academic and real-world problem-solving scenarios. Continuous practice through the provided exercises will further reinforce understanding and proficiency.
In summary, the expression \(5 \sqrt{x}\) is a fundamental mathematical function with wide-ranging applications. A solid grasp of its properties, graphing, and applications can significantly enhance one's mathematical toolkit.
Video hướng dẫn đơn giản hóa biểu thức căn bậc hai của x^5. Tìm hiểu cách làm một cách dễ hiểu và chính xác.
Đơn Giản Biểu Thức Radial: Căn Bậc Hai của x^5
READ MORE:
Khám phá cách đơn giản hóa phép tính căn bậc hai một cách tuyệt vời và tìm giá trị của X trong video này.
Phép Đơn Giản Hóa Căn Bậc Hai Tuyệt Vời | Tìm Giá Trị của X