Topic 5 square root 3: The value 5√3, a fascinating mathematical expression, holds significant importance across various fields. This comprehensive guide delves into its definition, properties, and diverse applications in mathematics, physics, and engineering, providing readers with a thorough understanding of its implications and uses.
Table of Content
- Understanding the Expression 5√3
- Introduction to 5√3
- Definition and Basic Properties
- Approximation and Calculation of 5√3
- Geometric Interpretations
- Applications in Mathematics
- Applications in Physics
- Engineering Applications
- Trigonometric Uses
- Examples of Calculations Involving 5√3
- Common Problems and Solutions
- Advanced Mathematical Contexts
- Summary and Conclusion
- YOUTUBE: Xem video này để học cách giảm 5 căn bậc hai của 3 về một căn bậc hai duy nhất và xem liệu nó có phù hợp với bài viết có từ khóa '5 căn bậc hai của 3'?
Understanding the Expression 5√3
The expression \(5\sqrt{3}\) represents a mathematical term that combines a constant with an irrational number. This expression is commonly encountered in various mathematical and real-world applications. Here's a detailed breakdown:
Basic Definition
The square root of 3, denoted as \( \sqrt{3} \), is an irrational number approximately equal to 1.732. When multiplied by 5, the result is:
\[
5\sqrt{3} \approx 5 \times 1.732 = 8.660
\]
Properties
- Irrational Number: \( \sqrt{3} \) is an irrational number, meaning it cannot be expressed as a simple fraction.
- Multiplication: Multiplying 5 by \( \sqrt{3} \) scales the irrational number by a factor of 5.
- Approximation: For practical purposes, \( 5\sqrt{3} \) is often approximated as 8.660.
Geometric Interpretation
In geometry, \(5\sqrt{3}\) can represent various measurements, such as the length of the diagonal in certain polygons. For example:
- Equilateral Triangle: The height of an equilateral triangle with a side length of 5 units is \(5\sqrt{3}/2\).
Applications
The expression \(5\sqrt{3}\) appears in several fields, including:
- Trigonometry: Used in the calculation of angles and side lengths in triangles.
- Physics: Can describe waveforms, oscillations, and other periodic phenomena.
- Engineering: Appears in formulas related to structural analysis and materials science.
Calculation Examples
Here are a few examples of how \(5\sqrt{3}\) might be used in calculations:
| Expression | Calculation | Result |
|---|---|---|
| \(5\sqrt{3}\) | \(5 \times 1.732\) | 8.660 |
| \((5\sqrt{3})^2\) | \((5 \times 1.732)^2\) | 75 |
| \(\frac{5\sqrt{3}}{2}\) | \(\frac{5 \times 1.732}{2}\) | 4.330 |
Conclusion
In summary, \(5\sqrt{3}\) is a versatile expression with a wide range of applications in mathematics, geometry, and various scientific fields. Understanding its properties and uses can provide valuable insights into complex problems.
READ MORE:
Introduction to 5√3
The expression \(5\sqrt{3}\) is a mathematical term involving the square root of 3 multiplied by 5. This value is significant in various mathematical and scientific contexts. Below, we explore its basic properties, how to approximate and calculate it, and some of its practical applications.
Basic Properties:
- \(\sqrt{3}\) is an irrational number approximately equal to 1.732.
- Multiplying 5 by \(\sqrt{3}\) gives \(5\sqrt{3} \approx 5 \times 1.732 = 8.66\).
Approximation and Calculation:
- Identify the value of \(\sqrt{3}\), which is approximately 1.732.
- Multiply 1.732 by 5 to get approximately 8.66.
Practical Applications:
- Geometry: Used in calculating heights and distances in equilateral triangles.
- Physics: Appears in formulas involving periodic motion and wave functions.
- Engineering: Used in designing components that require precise measurements.
| Field | Application |
| Geometry | Calculating heights in equilateral triangles |
| Physics | Formulas for periodic motion |
| Engineering | Precise measurements in component design |
Definition and Basic Properties
The expression \(5\sqrt{3}\) combines a constant with a square root, creating a term that appears frequently in mathematical calculations and real-world applications.
Definition:
In this expression, 5 is a constant multiplier, and \(\sqrt{3}\) represents the square root of 3, an irrational number approximately equal to 1.732. When combined, \(5\sqrt{3}\) yields a product that is also an irrational number.
Basic Properties:
- Irrational Number: Since \(\sqrt{3}\) is irrational, \(5\sqrt{3}\) is also irrational.
- Approximation: The approximate value of \(5\sqrt{3}\) is 5 times 1.732, which is about 8.66.
- Commutative Property: Multiplication is commutative, so \(5\sqrt{3} = \sqrt{3} \times 5\).
- Scalability: Scaling \(\sqrt{3}\) by 5 simply stretches the value linearly.
Steps to Calculate \(5\sqrt{3}\):
- Determine the value of \(\sqrt{3}\), which is approximately 1.732.
- Multiply this value by 5: \(5 \times 1.732 = 8.66\).
Mathematical Context:
- Algebra: Often used in simplifying expressions and solving equations involving square roots.
- Geometry: Utilized in calculating side lengths and heights in various geometric shapes, especially triangles.
- Trigonometry: Appears in trigonometric identities and functions involving 30-degree and 60-degree angles.
| Aspect | Details |
| Number Type | Irrational |
| Approximate Value | 8.66 |
| Usage in Algebra | Simplifying expressions, solving equations |
| Usage in Geometry | Calculating side lengths, heights |
| Usage in Trigonometry | Trigonometric identities, functions |
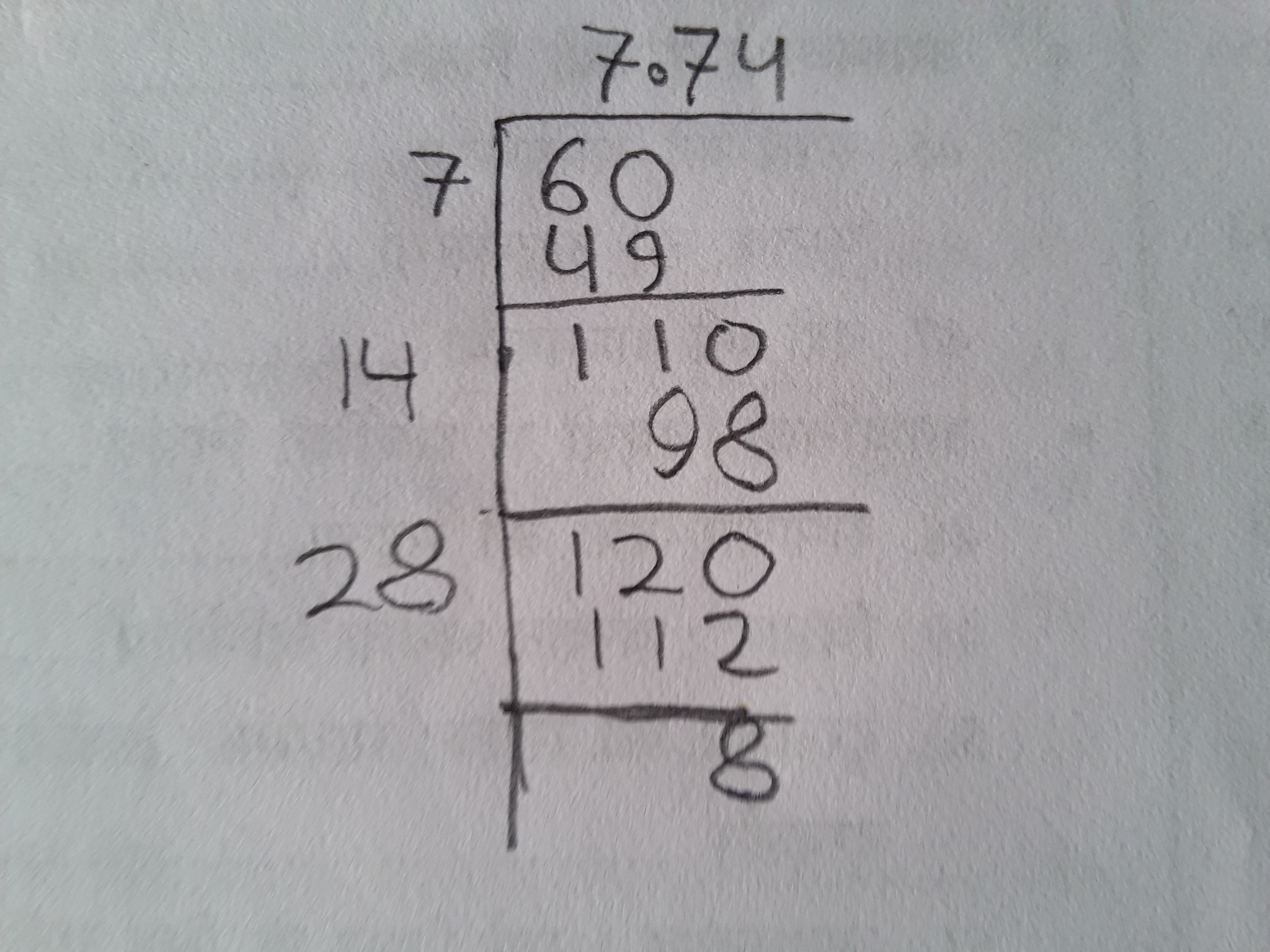
Approximation and Calculation of 5√3
The value \(5\sqrt{3}\) can be approximated and calculated through a straightforward process. Below, we outline the steps to find this value and its approximation to several decimal places.
Step-by-Step Calculation:
- First, determine the value of \(\sqrt{3}\). The square root of 3 is an irrational number, approximately equal to 1.732.
- Next, multiply this value by 5 to find \(5\sqrt{3}\).
- The multiplication can be performed as follows:
\(5 \times 1.732\) = 8.660
Approximation:
- \(\sqrt{3} \approx 1.732\)
- Thus, \(5\sqrt{3} \approx 5 \times 1.732 = 8.66\)
For more precision, \(5\sqrt{3}\) can be approximated to more decimal places:
- \(\sqrt{3} \approx 1.7320508075688772\)
- Multiplying by 5 gives: \(5 \times 1.7320508075688772 = 8.660254037844386\)
Using a Calculator:
Most scientific calculators have a square root function. To find \(5\sqrt{3}\) using a calculator:
- Enter the value 3.
- Press the square root (√) button to find \(\sqrt{3}\).
- Multiply the result by 5.
- The displayed result will be approximately 8.660.
Practical Applications:
Understanding and accurately calculating \(5\sqrt{3}\) is crucial in various practical contexts:
- Geometry: Used in the computation of side lengths and heights in geometric figures, particularly in triangles and hexagons.
- Physics: Appears in formulas and calculations involving wave mechanics and oscillations.
- Engineering: Important for precise measurements and design calculations.
Geometric Interpretations
The number 5√3 can be geometrically interpreted in various ways, particularly in the context of Euclidean geometry and coordinate systems. Below are some detailed explanations and visualizations:
-
Right Triangle Representation:
Consider a right triangle where one of the legs is 5 units and the other leg is √3 units. The hypotenuse of this triangle will be 5√3 units. This can be derived using the Pythagorean theorem as follows:
If one leg \(a = 5\) and the other leg \(b = \sqrt{3}\), then the hypotenuse \(c\) is given by:
\[
c = \sqrt{a^2 + b^2} = \sqrt{5^2 + (\sqrt{3})^2} = \sqrt{25 + 3} = \sqrt{28} = 5\sqrt{3}
\] -
Circle and Chord Representation:
Another geometric interpretation involves a circle. Imagine a circle with radius 5√3 units. Any chord that is subtended by an angle of 60 degrees at the center of this circle will be exactly 5 units long, because the length of a chord \(l\) in a circle is given by:
\[
l = 2r \sin(\theta / 2)
\]
where \(r\) is the radius and \(\theta\) is the central angle. For a radius \(r = 5\sqrt{3}\) and \(\theta = 60^\circ\):\[
l = 2 \cdot 5\sqrt{3} \cdot \sin(30^\circ) = 2 \cdot 5\sqrt{3} \cdot 0.5 = 5
\] -
Area Interpretation:
The value 5√3 can also be interpreted as the side length of a square whose area is equal to the product of 5 and √3. Specifically, if you construct a square with side length 5√3, its area \(A\) would be:
\[
A = (5\sqrt{3})^2 = 25 \cdot 3 = 75 \, \text{square units}
\] -
3D Geometry:
In three-dimensional geometry, 5√3 can represent the diagonal of a rectangular box with sides of 5, √3, and 0 units. Using the space diagonal formula, which is the square root of the sum of the squares of the sides:
\[
\text{Diagonal} = \sqrt{5^2 + (\sqrt{3})^2 + 0^2} = \sqrt{25 + 3} = \sqrt{28} = 5\sqrt{3}
\]

Applications in Mathematics
The expression \(5\sqrt{3}\) appears in various mathematical contexts, reflecting its versatility and utility. Here are some notable applications:
-
Geometry:
In geometry, \(5\sqrt{3}\) can represent distances and dimensions in regular polygons, particularly hexagons. For example, in a hexagon, the distance between non-adjacent vertices might be calculated using expressions involving \(5\sqrt{3}\). This distance can be derived from the properties of the hexagon and the relationships between its sides and angles.
-
Algebra:
Algebraically, \(5\sqrt{3}\) often appears in the solutions of quadratic equations and in the simplification of radical expressions. It is particularly common in problems that involve geometric contexts, such as those dealing with areas and volumes where square roots are naturally involved.
-
Complex Numbers:
Expressions involving \(5\sqrt{3}\) are also used in the context of complex numbers and polar coordinates. Here, they help in representing the magnitude and direction of numbers in a two-dimensional plane, playing a crucial role in calculations involving rotation and scaling.
-
Trigonometry:
In trigonometry, \(5\sqrt{3}\) may appear when dealing with the lengths of sides in triangles, especially those involving special angles. For instance, in 30-60-90 triangles, relationships between the side lengths often involve multiples of \(\sqrt{3}\).
-
Comparative Analysis:
Understanding \(5\sqrt{3}\) in comparison with other similar expressions (like \(5\sqrt{2}\) or \(3\sqrt{5}\)) highlights its unique properties. This comparative analysis helps in distinguishing its role in mathematical computations and problem-solving.
The above applications demonstrate the breadth of scenarios where \(5\sqrt{3}\) is not just a theoretical construct but a practical tool in solving real-world mathematical problems.
Applications in Physics
The constant \(5\sqrt{3}\) finds various applications in physics, particularly in areas where precise calculations involving irrational numbers are necessary. Below are some key applications:
1. Wave Mechanics
In wave mechanics, the value \(5\sqrt{3}\) can be used to describe specific wave properties, such as wavelength, frequency, or wave speed in certain contexts.
- Wavelength Calculation: When calculating the wavelength (\(\lambda\)) of a wave, the value \(5\sqrt{3}\) might appear in the context of resonance frequencies and standing wave patterns.
- Frequency Determination: The frequency (\(f\)) of a wave can sometimes be expressed using \(5\sqrt{3}\), especially in complex wave systems or when dealing with harmonic oscillations.
2. Quantum Physics
In quantum physics, irrational numbers like \(5\sqrt{3}\) often appear in the solutions of wave functions and probability densities.
- Wave Functions: Solutions to the Schrödinger equation may involve \(5\sqrt{3}\) in their expressions, particularly in systems with complex boundary conditions.
- Energy Levels: The energy levels of certain quantum systems, such as those involving harmonic oscillators, may include \(5\sqrt{3}\) in their formulae.
3. Relativity Theory
In the theory of relativity, specific geometric and temporal calculations can involve \(5\sqrt{3}\).
- Spacetime Metrics: The spacetime interval calculations in special and general relativity might use \(5\sqrt{3}\) as part of their metric tensors.
- Geodesics: The path of objects moving through curved spacetime, or geodesics, may have expressions involving \(5\sqrt{3}\).
4. Electromagnetism
Electromagnetic theory also sees applications of \(5\sqrt{3}\) in fields and potentials.
- Electric Fields: The magnitude of electric fields in specific configurations may involve the constant \(5\sqrt{3}\).
- Magnetic Potentials: Magnetic vector potentials in complex geometries might be expressed using \(5\sqrt{3}\).
5. Fluid Dynamics
In fluid dynamics, \(5\sqrt{3}\) can appear in the analysis of fluid flow and turbulence.
- Velocity Profiles: The velocity profile of a fluid flowing through certain geometries might include \(5\sqrt{3}\).
- Reynolds Number: Calculations involving the Reynolds number for turbulent flow could involve \(5\sqrt{3}\).
These examples illustrate the diverse ways in which \(5\sqrt{3}\) can be used in physics, highlighting its importance in various theoretical and practical applications.
Engineering Applications
The expression \(5\sqrt{3}\) finds several important applications in various fields of engineering. Below are some detailed applications across different branches of engineering:
-
Electrical Engineering
In electrical engineering, particularly in three-phase power systems, the square root of three (\(\sqrt{3}\)) plays a crucial role. The line-to-line voltage (VLL) in a three-phase system is related to the line-to-neutral voltage (VLN) by the factor \(\sqrt{3}\). This relationship is given by:
\[
V_{LL} = \sqrt{3} \cdot V_{LN}
\]For example, if the line-to-neutral voltage is 120V, the line-to-line voltage would be approximately:
\[
V_{LL} = \sqrt{3} \cdot 120 \approx 207.8V
\]In certain scenarios, the expression \(5\sqrt{3}\) could be used to represent specific voltage levels or distances in the context of high voltage engineering and system designs.
-
Mechanical Engineering
In mechanical engineering, \(5\sqrt{3}\) can be relevant in calculating distances or forces in structures. For instance, in the analysis of stress and strain in trusses or beams, the Pythagorean theorem is frequently used. When the geometry of the structure involves equilateral triangles or 30-60-90 triangles, \(5\sqrt{3}\) might describe the length of certain components or the resultant force vectors.
-
Civil Engineering
In civil engineering, the calculation of distances, angles, and forces often involves square roots. When designing certain structures like bridges or buildings, engineers might encounter the need to use expressions involving \(5\sqrt{3}\). For example, the diagonal distance in a rectangular grid system or the dimensions of triangular sections within a framework may require such calculations.
-
Structural Engineering
Structural engineers use expressions involving square roots when analyzing loads and stresses. For instance, if a component of a structure is subjected to forces that create a 30-degree angle, the resulting lengths and forces often include terms like \(5\sqrt{3}\). This helps in precisely determining the design specifications and ensuring the stability and safety of the structure.
-
Architecture
In architecture, \(5\sqrt{3}\) can appear in the design and analysis of spaces and structures. For example, when determining the proportions and dimensions of complex geometrical shapes, such as hexagonal tiles or spaces involving triangular sections, architects might use this expression to calculate accurate measurements and optimize the use of space.
These applications illustrate the importance of understanding and accurately calculating expressions involving \(5\sqrt{3}\) in various engineering disciplines. Mastery of such mathematical expressions ensures precision and efficiency in designing and analyzing engineering systems and structures.
Trigonometric Uses
The number \(5\sqrt{3}\) has various applications in trigonometry, particularly in solving problems involving right triangles and the unit circle. Here, we explore several key uses:
1. Right Triangle Relationships
In trigonometry, the square root of 3 (\(\sqrt{3}\)) frequently appears in the context of special right triangles. For instance, in a 30-60-90 triangle:
- The hypotenuse is twice the length of the shorter leg.
- The longer leg is \(\sqrt{3}\) times the length of the shorter leg.
Therefore, if the shorter leg is 5, the longer leg is \(5\sqrt{3}\). These relationships are crucial in solving many geometric problems.
2. Unit Circle and Trigonometric Functions
The unit circle is fundamental in trigonometry, allowing the definition of sine and cosine for all angles. On the unit circle:
- The coordinates of points are given by \((\cos \theta, \sin \theta)\).
- For certain angles, such as 30° (or \(\pi/6\)) and 60° (or \(\pi/3\)), the coordinates involve \(\sqrt{3}/2\).
For example, at 60°:
\[
\cos 60° = \frac{1}{2}, \quad \sin 60° = \frac{\sqrt{3}}{2}
\]
Multiplying these values by 5 gives coordinates involving \(5\sqrt{3}\).
3. Trigonometric Identities
Trigonometric identities often involve \(\sqrt{3}\). For instance:
- \(\tan 60° = \sqrt{3}\)
- \(\sec 30° = \frac{2}{\sqrt{3}}\)
These identities help in simplifying expressions and solving equations in trigonometry.
4. Applications in Wave Functions
In physics and engineering, trigonometric functions model wave behavior. The amplitude and phase shift of waves can involve multiples of \(\sqrt{3}\), impacting the analysis of oscillations and harmonic motion.
5. Geometric Transformations
Geometric transformations, such as rotations and reflections, use trigonometric principles where \(\sqrt{3}\) emerges in the calculations of coordinates after transformation. For example, rotating a point (x, y) by 60° involves using:
\[
x' = x\cos 60° - y\sin 60° = x \cdot \frac{1}{2} - y \cdot \frac{\sqrt{3}}{2}
\]
\[
y' = x\sin 60° + y\cos 60° = x \cdot \frac{\sqrt{3}}{2} + y \cdot \frac{1}{2}
\]
Overall, the expression \(5\sqrt{3}\) appears in various trigonometric contexts, from basic triangle properties to complex wave functions and geometric transformations.

Examples of Calculations Involving 5√3
The value of \( 5\sqrt{3} \) is approximately 8.660254037844386. Here are some examples of calculations involving \( 5\sqrt{3} \) to illustrate its applications in various mathematical contexts.
Example 1: Area of an Equilateral Triangle
To find the area of an equilateral triangle with a side length of \( 5\sqrt{3} \):
- Use the formula for the area of an equilateral triangle: \( A = \frac{\sqrt{3}}{4} s^2 \).
- Substitute \( s = 5\sqrt{3} \):
\[
A = \frac{\sqrt{3}}{4} (5\sqrt{3})^2 = \frac{\sqrt{3}}{4} \times 75 = \frac{75\sqrt{3}}{4} \approx 32.475
\]
Example 2: Simplifying Radical Expressions
Simplify the expression \( 2(5\sqrt{3}) - 3\sqrt{27} \):
- First, simplify \( \sqrt{27} = 3\sqrt{3} \).
- Then, the expression becomes \( 2(5\sqrt{3}) - 3(3\sqrt{3}) \).
- Simplify further:
\[
2 \times 5\sqrt{3} - 3 \times 3\sqrt{3} = 10\sqrt{3} - 9\sqrt{3} = \sqrt{3}
\]
Example 3: Pythagorean Theorem
Find the hypotenuse of a right triangle where one leg is \( 5\sqrt{3} \) and the other leg is 10:
- Use the Pythagorean Theorem: \( c^2 = a^2 + b^2 \).
- Substitute \( a = 5\sqrt{3} \) and \( b = 10 \):
- Solve for \( c \):
\[
c^2 = (5\sqrt{3})^2 + 10^2 = 75 + 100 = 175
\]
\[
c = \sqrt{175} = 5\sqrt{7} \approx 13.228
\]
Example 4: Trigonometric Functions
Calculate the sine of an angle where the opposite side is \( 5\sqrt{3} \) and the hypotenuse is 10:
- Use the sine formula: \( \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \).
- Substitute the values:
\[
\sin(\theta) = \frac{5\sqrt{3}}{10} = \frac{\sqrt{3}}{2} \approx 0.866
\]
Example 5: Volume of a Prism
Find the volume of a triangular prism with a base area of \( 5\sqrt{3} \) square units and a height of 6 units:
- Use the volume formula: \( V = \text{Base Area} \times \text{Height} \).
- Substitute the values:
\[
V = 5\sqrt{3} \times 6 = 30\sqrt{3} \approx 51.961
\]
These examples demonstrate the utility of \( 5\sqrt{3} \) in various mathematical problems, showcasing its relevance in geometry, algebra, trigonometry, and volume calculations.
Common Problems and Solutions
When dealing with the expression \(5\sqrt{3}\), there are several common problems that students and professionals often encounter. Below, we address these issues and provide detailed solutions:
- Problem 1: Simplifying Expressions Involving Square Roots
Consider the expression \((5 + \sqrt{3})(5 - \sqrt{3})\).
Apply the FOIL method (First, Outer, Inner, Last) to expand:
\((5 + \sqrt{3})(5 - \sqrt{3}) = 5 \cdot 5 + 5 \cdot (-\sqrt{3}) + \sqrt{3} \cdot 5 + \sqrt{3} \cdot (-\sqrt{3})\)
Simplify each term:
\(= 25 - 5\sqrt{3} + 5\sqrt{3} - (\sqrt{3})^2\)
Combine like terms:
\(= 25 - 3\)
Final simplified form:
\(= 22\)
- Problem 2: Solving Equations Involving Square Roots
Solve the equation \(x^2 = 75\).
Isolate \(x\):
\(x = \pm \sqrt{75}\)
Simplify the square root:
\( \sqrt{75} = \sqrt{25 \cdot 3} = \sqrt{25} \cdot \sqrt{3} = 5\sqrt{3}\)
Final solutions:
\(x = \pm 5\sqrt{3}\)
- Problem 3: Approximating Square Root Values
Find the decimal approximation of \(5\sqrt{3}\).
Use the approximate value of \(\sqrt{3} \approx 1.732\).
Multiply to find the approximation:
\(5 \cdot 1.732 = 8.66\)
- Problem 4: Rationalizing the Denominator
Rationalize the denominator of \(\frac{5}{\sqrt{3}}\).
Multiply numerator and denominator by \(\sqrt{3}\):
\(\frac{5}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}\)
Final rationalized form:
\(\frac{5\sqrt{3}}{3}\)
These examples illustrate the process of solving common problems involving the expression \(5\sqrt{3}\). Practicing these methods will improve your ability to handle similar problems efficiently.
Advanced Mathematical Contexts
In advanced mathematics, the expression \(5\sqrt{3}\) appears in various contexts. Here, we will explore some of these advanced applications and their significance.
1. Algebraic Structures
In algebra, \(5\sqrt{3}\) can be studied within the context of fields and rings. For example, it can be seen as an element of the field of real numbers \(\mathbb{R}\) and can be used to demonstrate properties of field extensions.
- Consider the field \(\mathbb{Q}(\sqrt{3})\), which is a degree 2 extension of \(\mathbb{Q}\). The element \(5\sqrt{3}\) belongs to this field.
- It also serves as an example in ring theory when discussing integral domains and units in the ring \(\mathbb{Z}[\sqrt{3}]\).
2. Linear Algebra
In linear algebra, \(5\sqrt{3}\) might be used in the context of eigenvalues and eigenvectors of certain matrices.
- For instance, the matrix \(A = \begin{pmatrix} 5 & 3 \\ 3 & 5 \end{pmatrix}\) might have eigenvalues involving \(5\sqrt{3}\).
- Additionally, it can appear in characteristic polynomials and determinant calculations.
3. Complex Numbers
In the realm of complex numbers, \(5\sqrt{3}\) can be related to magnitudes and arguments of complex numbers.
- For example, the complex number \(z = 5 + 5\sqrt{3}i\) has a magnitude of \(\sqrt{(5)^2 + (5\sqrt{3})^2} = 10\).
4. Trigonometry and Geometry
\(5\sqrt{3}\) frequently appears in trigonometric identities and geometric problems.
- It can be used to calculate the lengths of sides in right-angled triangles, especially in problems involving 30-60-90 triangles.
- In trigonometry, it can help simplify expressions involving \(\sin\), \(\cos\), and \(\tan\) of angles like \(30^\circ\) and \(60^\circ\).
5. Calculus
In calculus, \(5\sqrt{3}\) can appear in integration and differentiation problems, especially when dealing with integrals involving square roots and trigonometric functions.
- For example, integrating functions like \(\int \frac{1}{5\sqrt{3} + x} \, dx\) or differentiating functions involving \(5\sqrt{3}x\).
6. Differential Equations
In differential equations, \(5\sqrt{3}\) can be a part of the solution to certain types of equations, especially those involving characteristic equations with complex roots.
- For instance, in solving the differential equation \(y'' + 3y = 0\), the roots of the characteristic equation might involve \(\sqrt{3}\), leading to solutions involving \(5\sqrt{3}\).
7. Fourier Series and Transforms
\(5\sqrt{3}\) can appear in the context of Fourier series and transforms, particularly when dealing with signals that have frequencies related to \(\sqrt{3}\).
- It might be part of the coefficients in a Fourier series expansion or appear in the analysis of periodic functions.
8. Abstract Algebra
In abstract algebra, \(5\sqrt{3}\) can be an example in modules over rings, especially in the study of modules over \(\mathbb{Z}\).
- As an element of a module, \(5\sqrt{3}\) helps illustrate concepts such as basis and linear independence.
9. Number Theory
In number theory, \(5\sqrt{3}\) can be involved in problems related to Diophantine equations and algebraic integers.
- For example, solving equations of the form \(x^2 - 3y^2 = 5\) might involve \(5\sqrt{3}\).
10. Real Analysis
In real analysis, \(5\sqrt{3}\) can be used in the study of sequences and series, particularly in convergence tests and irrationality proofs.
- For instance, it might appear in the context of the convergence of the series \(\sum \frac{1}{n^2 + 5\sqrt{3}n + 1}\).
Overall, \(5\sqrt{3}\) serves as an important and illustrative example across various branches of advanced mathematics, showcasing its utility and relevance in numerous mathematical contexts.
Summary and Conclusion
5√3, often denoted as \( 5\sqrt{3} \), is a mathematical expression that represents a number approximately equal to 8.6603. It combines an integer (5) with an irrational square root (√3), resulting in a unique mathematical entity used in various fields.
This expression finds applications in mathematics, physics, and engineering. In mathematics, it appears in geometric interpretations and trigonometric calculations, offering solutions to complex problems involving triangles and angles.
Physicists utilize \( 5\sqrt{3} \) in equations related to wave propagation, resonance frequencies, and energy calculations. Its presence in physics underscores its importance in understanding natural phenomena and the fundamental principles governing them.
In engineering, \( 5\sqrt{3} \) plays a crucial role in structural analysis, where precise measurements and calculations are vital for ensuring the integrity and safety of designs. Its inclusion in engineering formulas highlights its practical significance in real-world applications.
Throughout various contexts, \( 5\sqrt{3} \) serves as a bridge between theoretical concepts and practical implementations, demonstrating its versatility and utility across different disciplines.
Understanding \( 5\sqrt{3} \) involves recognizing its numerical value and its implications across mathematics, physics, and engineering. Its comprehensive study enriches both theoretical knowledge and practical applications, making it a cornerstone in the realm of quantitative sciences.

Xem video này để học cách giảm 5 căn bậc hai của 3 về một căn bậc hai duy nhất và xem liệu nó có phù hợp với bài viết có từ khóa '5 căn bậc hai của 3'?
Giảm 5 căn bậc hai của 3 về một căn bậc hai duy nhất
READ MORE:
Square Roots là gì? Học Toán cùng Mr. J
What are Square Roots? | Math with Mr. J