Topic 5 square root 7: Discover the fascinating world of square roots with our detailed guide on calculating 5 square root 7. This article breaks down the steps, explains the importance of square roots in mathematics, and provides practical applications. Join us on a journey to master this essential mathematical concept and enhance your problem-solving skills.
Table of Content
- Understanding the Expression \(5 \sqrt{7}\)
- Introduction to Square Roots
- Basic Properties of Square Roots
- Understanding the Expression 5 Square Root 7
- Calculating 5 Square Root 7
- Applications of Square Roots in Real Life
- Mathematical Importance of Square Roots
- Visualizing Square Roots
- Historical Context of Square Roots
- Advanced Topics in Square Roots
- Common Mistakes with Square Roots
- Practice Problems Involving 5 Square Root 7
- Conclusion and Further Reading
- YOUTUBE: Học về căn bậc hai và ứng dụng của chúng trong toán học với thầy J.
Understanding the Expression \(5 \sqrt{7}\)
The expression \(5 \sqrt{7}\) combines a rational number (5) with an irrational number (the square root of 7). It is often encountered in mathematical problems and can be used in various contexts such as algebra, geometry, and calculus.
Calculation and Approximation
The value of \(\sqrt{7}\) is approximately 2.64575. Therefore, the expression \(5 \sqrt{7}\) can be calculated as:
\[
5 \sqrt{7} \approx 5 \times 2.64575 = 13.22875
\]
Applications
The expression \(5 \sqrt{7}\) can be found in different mathematical contexts, including:
- Solving quadratic equations
- Trigonometric identities
- Geometric measurements
Visual Representation
To visualize \(5 \sqrt{7}\), imagine a right triangle where one of the legs is 5 units and the hypotenuse involves the square root of 7. This can be depicted graphically for better understanding.
Properties
Here are some properties of the expression \(5 \sqrt{7}\):
- Irrationality: Since \(\sqrt{7}\) is irrational, the product \(5 \sqrt{7}\) is also irrational.
- Simplification: The expression cannot be simplified further without approximating \(\sqrt{7}\).
Examples
| Example 1: | Simplify \(5 \sqrt{7} \times 2\) | \[ 5 \sqrt{7} \times 2 = 10 \sqrt{7} \] |
| Example 2: | Find the value of \((5 \sqrt{7})^2\) | \[ (5 \sqrt{7})^2 = 25 \times 7 = 175 \] |
READ MORE:
Introduction to Square Roots
Square roots are fundamental in mathematics, representing a number that, when multiplied by itself, gives the original number. For example, the square root of 49 is 7 because \(7 \times 7 = 49\). The square root symbol is \( \sqrt{} \), and it denotes the principal or non-negative root.
Here are the key properties of square roots:
- Non-negative results: The square root of a non-negative number is also non-negative.
- Multiplication property: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- Division property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) for \(b \neq 0\)
- Perfect squares: Numbers like 1, 4, 9, 16, etc., whose square roots are integers.
To better understand, let’s consider the expression \(5 \sqrt{7}\). This is a combination of a whole number (5) and an irrational number (\(\sqrt{7}\)), which is approximately 2.64575. Thus:
- Identify the square root part: \(\sqrt{7} \approx 2.64575\)
- Multiply by 5: \(5 \times 2.64575 \approx 13.22875\)
Square roots are used in various applications, from solving quadratic equations to understanding geometric properties and real-world measurements. Mastering square roots enhances your mathematical abilities and problem-solving skills.
Basic Properties of Square Roots
Square roots possess several fundamental properties that are essential for understanding and performing mathematical operations. Here, we will explore these properties in detail:
- Non-negative Results: The square root of any non-negative number is always non-negative. For instance, \( \sqrt{16} = 4 \) and \( \sqrt{0} = 0 \).
- Multiplication Property: The square root of a product is the product of the square roots of the factors. This can be written as: \[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \] For example, \( \sqrt{36} = \sqrt{9 \times 4} = \sqrt{9} \times \sqrt{4} = 3 \times 2 = 6 \).
- Division Property: The square root of a quotient is the quotient of the square roots of the numerator and the denominator, provided the denominator is not zero: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}, \quad b \neq 0 \] For example, \( \sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} = 2.5 \).
- Power Property: The square root of a number raised to an even power is the number raised to half the power: \[ \sqrt{a^2} = a \] This means \( \sqrt{16} = \sqrt{4^2} = 4 \).
- Perfect Squares: A perfect square is an integer that is the square of another integer. The square root of a perfect square is always an integer. Examples include:
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
To illustrate these properties, consider the expression \(5 \sqrt{7}\). Applying these properties, we can see how they simplify and clarify the calculation process:
- Recognize that \(\sqrt{7}\) is an irrational number, approximately equal to 2.64575.
- Multiply by 5 to get: \[ 5 \times \sqrt{7} \approx 5 \times 2.64575 = 13.22875 \]
Understanding these basic properties of square roots is crucial for solving more complex mathematical problems and for practical applications in various fields.
Understanding the Expression 5 Square Root 7
The expression \(5 \sqrt{7}\) combines a whole number with a square root, creating a valuable mathematical construct. Let's break down this expression to understand its components and how they work together.
Step-by-Step Breakdown:
- Identify the Square Root: The term \(\sqrt{7}\) represents the square root of 7. Since 7 is not a perfect square, \(\sqrt{7}\) is an irrational number, approximately equal to 2.64575.
- Multiply by 5: In the expression \(5 \sqrt{7}\), the 5 is a coefficient that scales the square root of 7. We multiply 5 by \(\sqrt{7}\) to get the final value: \[ 5 \times \sqrt{7} \approx 5 \times 2.64575 = 13.22875 \]
To ensure clarity, here are the steps presented in a more visual format:
| Step | Description | Calculation |
| 1 | Identify the square root of 7 | \(\sqrt{7} \approx 2.64575\) |
| 2 | Multiply by the coefficient 5 | \(5 \times 2.64575 \approx 13.22875\) |
Applications and Importance:
- Mathematical Problems: Expressions like \(5 \sqrt{7}\) are common in algebra, geometry, and higher mathematics. They are used in solving equations, understanding geometric dimensions, and more.
- Practical Applications: In real-world scenarios, such expressions can be found in measurements, physics problems, and engineering calculations. For instance, they might represent lengths, areas, or other quantities where precise calculations are necessary.
Understanding the expression \(5 \sqrt{7}\) not only enhances your mathematical skills but also prepares you for various practical and theoretical applications. By mastering such expressions, you can tackle more complex problems with confidence and accuracy.
Calculating 5 Square Root 7
The expression \(5 \sqrt{7}\) combines the constant 5 with the square root of 7. Calculating this involves straightforward multiplication. Let's go through the process step by step to ensure clarity and accuracy.
Step-by-Step Calculation:
- Determine the Square Root: First, we need to find the square root of 7. Since 7 is not a perfect square, its square root is an irrational number: \[ \sqrt{7} \approx 2.64575 \]
- Multiply by 5: Next, we multiply the result by 5: \[ 5 \times \sqrt{7} = 5 \times 2.64575 \]
- Calculate the Product: Performing the multiplication gives us the final value: \[ 5 \times 2.64575 = 13.22875 \]
To summarize the process in a visual format:
| Step | Action | Result |
| 1 | Find \(\sqrt{7}\) | \(\sqrt{7} \approx 2.64575\) |
| 2 | Multiply by 5 | \(5 \times 2.64575\) |
| 3 | Calculate the product | \(13.22875\) |
Thus, the value of \(5 \sqrt{7}\) is approximately 13.22875. This result is useful in various mathematical contexts, from solving equations to practical applications in science and engineering.
Why It Matters:
- Precision: Understanding how to accurately calculate expressions like \(5 \sqrt{7}\) is crucial for precision in mathematical and scientific work.
- Application: Such calculations often appear in geometry, physics, and engineering problems, where exact measurements and results are necessary.
- Confidence: Mastering these steps builds confidence in handling more complex mathematical expressions and enhances problem-solving skills.

Applications of Square Roots in Real Life
Square roots are fundamental in mathematics and play a crucial role in various real-life applications. Understanding and utilizing square roots can enhance problem-solving skills and practical knowledge in multiple fields.
Key Applications of Square Roots:
- Geometry and Trigonometry: Square roots are essential in calculating distances, areas, and volumes. For example, the Pythagorean theorem involves square roots to find the length of the hypotenuse in a right-angled triangle: \[ c = \sqrt{a^2 + b^2} \]
- Physics and Engineering: Square roots are used in formulas to determine forces, velocities, and other physical properties. For instance, in the equation for gravitational potential energy: \[ v = \sqrt{2gh} \] where \(v\) is the velocity, \(g\) is the acceleration due to gravity, and \(h\) is the height.
- Finance: Square roots help in calculating compound interest and understanding financial models. The standard deviation, a measure of risk, is derived using square roots: \[ \sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}} \]
- Computer Science: Algorithms and data structures often involve square roots for optimization and efficiency. For example, finding the optimal block size in block sort algorithms: \[ O(\sqrt{n}) \]
- Astronomy: Calculating distances between celestial bodies and understanding the orbits of planets involve square roots. For example, the formula for escape velocity: \[ v_e = \sqrt{\frac{2GM}{r}} \] where \(v_e\) is the escape velocity, \(G\) is the gravitational constant, \(M\) is the mass of the planet, and \(r\) is the radius from the center of the planet.
Practical Examples:
- Construction and Architecture: Accurate measurements are critical, and square roots help in determining correct dimensions and angles, ensuring the stability and aesthetics of structures.
- Medicine: Dosage calculations for medications often use square roots to ensure proper administration based on patient weight and other factors.
- Navigation: GPS technology uses algorithms involving square roots to accurately calculate distances and positions on Earth's surface.
By mastering square roots, one can solve practical problems efficiently and apply mathematical principles effectively in various real-world situations.
Mathematical Importance of Square Roots
Square roots are a fundamental concept in mathematics, integral to various fields and applications. Understanding square roots is essential for solving complex problems and exploring advanced mathematical theories.
Key Reasons for the Importance of Square Roots:
- Basic Arithmetic and Algebra: Square roots are foundational in arithmetic operations and algebraic equations. They are used to solve quadratic equations, such as: \[ ax^2 + bx + c = 0 \] Using the quadratic formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
- Geometry: Square roots are crucial for calculating distances, areas, and volumes. The Pythagorean theorem relies on square roots to find the hypotenuse of a right triangle: \[ c = \sqrt{a^2 + b^2} \]
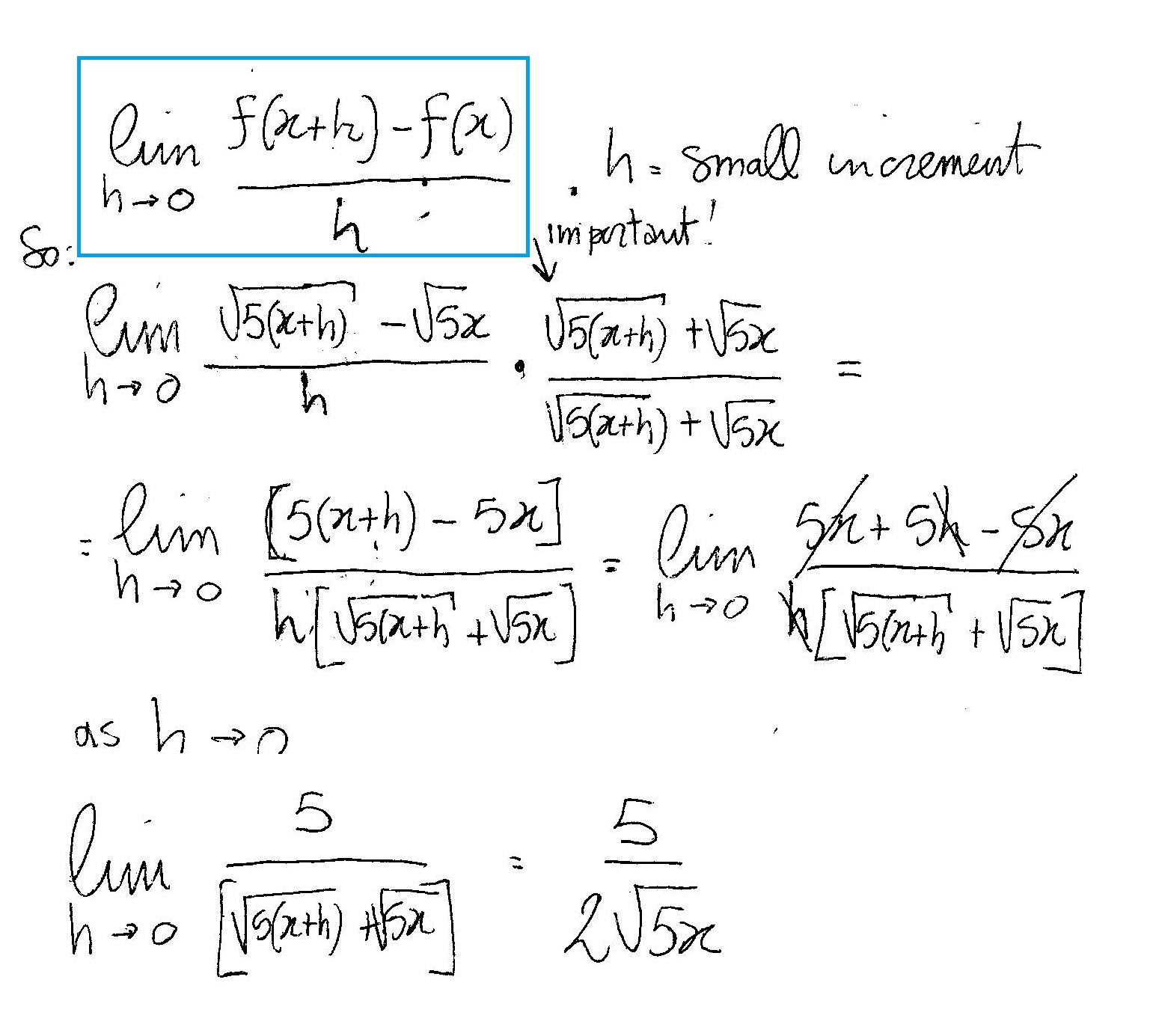
- Calculus: In calculus, square roots are involved in differentiation and integration, particularly when dealing with functions involving exponents and roots. For example: \[ \text{If } f(x) = \sqrt{x}, \text{ then } f'(x) = \frac{1}{2\sqrt{x}} \]
- Statistics: The standard deviation, a measure of data dispersion, involves square roots: \[ \sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}} \] where \(\sigma\) is the standard deviation, \(x_i\) are the data points, \(\mu\) is the mean, and \(N\) is the number of data points.
- Complex Numbers: Square roots are essential in understanding complex numbers, particularly the imaginary unit \(i\), where: \[ i = \sqrt{-1} \] This concept extends to solving polynomial equations and other advanced mathematical problems.
Applications and Advanced Concepts:
- Vector Mathematics: Calculating the magnitude of a vector involves square roots: \[ \| \mathbf{v} \| = \sqrt{v_1^2 + v_2^2 + \ldots + v_n^2} \] where \(\mathbf{v}\) is a vector with components \(v_1, v_2, \ldots, v_n\).
- Fourier Transforms: Square roots are used in Fourier transforms, which are critical in signal processing, physics, and engineering.
- Probability and Quantum Mechanics: Probability amplitudes in quantum mechanics involve complex square roots, affecting the behavior of particles at the quantum level.
By mastering square roots, students and professionals can better understand mathematical principles, solve a wide range of problems, and apply their knowledge to various scientific and practical fields.
Visualizing Square Roots
Visualizing square roots can help in understanding their properties and applications better. The square root of a number is a value that, when multiplied by itself, gives the original number. In this section, we will explore how to visualize the expression \( 5 \sqrt{7} \) using various methods.
Geometric Representation
One way to visualize square roots is through geometric shapes. A square with an area of 7 square units will have a side length equal to \( \sqrt{7} \). To represent \( 5 \sqrt{7} \), consider a line segment that is 5 times longer than the side of this square.
The length of the side of the square is approximately:
\[
\sqrt{7} \approx 2.6457513110645906
\]
Thus, the length of \( 5 \sqrt{7} \) can be visualized as:
\[
5 \times \sqrt{7} \approx 5 \times 2.6457513110645906 \approx 13.228756555322953
\]
Graphical Representation
To graphically represent \( 5 \sqrt{7} \), plot the square root function and mark the value of \( \sqrt{7} \). Then, scale this value by a factor of 5.
For example, on a graph where the x-axis represents numbers and the y-axis represents their square roots, plot the point (7, \( \sqrt{7} \)). To represent \( 5 \sqrt{7} \), draw a line from the origin to the point (7, \( 5 \times \sqrt{7} \)).
Tabular Representation
Another method to visualize square roots is using a table that lists the values of square roots for different numbers and their multiples.
| Number (n) | \(\sqrt{n}\) | \(5 \times \sqrt{n}\) |
|---|---|---|
| 1 | \(\sqrt{1} = 1\) | 5 |
| 2 | \(\sqrt{2} \approx 1.414\) | \(5 \times 1.414 \approx 7.07\) |
| 3 | \(\sqrt{3} \approx 1.732\) | \(5 \times 1.732 \approx 8.66\) |
| 4 | \(\sqrt{4} = 2\) | 10 |
| 7 | \(\sqrt{7} \approx 2.646\) | \(5 \times 2.646 \approx 13.23\) |
Using Number Line
A number line can also help visualize \( 5 \sqrt{7} \). Mark the point representing \( \sqrt{7} \) on the number line. Since \( \sqrt{7} \approx 2.6457513110645906 \), locate this point on the line. To visualize \( 5 \sqrt{7} \), measure five times the distance from the origin to \( \sqrt{7} \) on the number line.
By using these methods, you can better understand and visualize the value of \( 5 \sqrt{7} \) and the concept of square roots in general.
Historical Context of Square Roots
The concept of square roots has a rich history, spanning various cultures and eras, each contributing to its development and understanding.
Square roots were first explored in ancient civilizations. The Babylonians are known to have used methods for approximating square roots as early as 2000 BCE. Their approach, found in clay tablets, used a form of iterative numerical techniques similar to modern methods.
In ancient Egypt, the Rhind Mathematical Papyrus (circa 1650 BCE) contains problems that involve square roots, indicating their practical use in geometry and construction.
The Greeks made significant contributions to the theory of square roots. The mathematician Euclid, in his seminal work "Elements," described methods for finding square roots geometrically. His approach laid the groundwork for later algebraic methods.
In China, during the Han Dynasty (202 BCE – 220 CE), mathematicians developed sophisticated techniques for extracting square roots, as documented in "The Nine Chapters on the Mathematical Art." This text detailed algorithms that were remarkably advanced for their time, showcasing the Chinese expertise in numerical methods.
The Islamic Golden Age (8th to 14th century) saw further advancements in the understanding of square roots. Mathematicians like Al-Khwarizmi, often referred to as the father of algebra, introduced systematic methods for solving quadratic equations, including the use of square roots.
In Europe, during the Renaissance, the development of symbolic algebra by mathematicians such as François Viète and later René Descartes revolutionized the understanding and notation of square roots. The square root symbol (√), as we use it today, was first introduced by Christoph Rudolff in his book "Coss" (1525).
Overall, the historical journey of square roots reflects the broader development of mathematical thought across different cultures and eras. Each civilization built upon the knowledge of its predecessors, leading to the comprehensive understanding of square roots that we have today.

Advanced Topics in Square Roots
The concept of square roots extends beyond simple arithmetic and has profound implications in various branches of mathematics and applied sciences. Below are some advanced topics related to square roots:
- Imaginary and Complex Numbers:
Square roots of negative numbers are not defined in the set of real numbers. This leads to the concept of imaginary numbers, where \( \sqrt{-1} \) is denoted as \( i \). Complex numbers are then expressed in the form \( a + bi \), where \( a \) and \( b \) are real numbers.
- Algebraic Properties:
Understanding the properties of square roots in algebra is crucial for solving quadratic equations. For example, the solutions to \( x^2 = a \) are \( x = \sqrt{a} \) and \( x = -\sqrt{a} \). These principles are foundational in higher-level algebra and calculus.
- Irrational Numbers:
Square roots of non-perfect squares are irrational numbers, meaning they cannot be expressed as a simple fraction. Their decimal representations are non-repeating and non-terminating. For instance, \( \sqrt{7} \approx 2.6457513110645906\ldots \)
- Approximation Techniques:
Various methods exist to approximate square roots, such as the Newton-Raphson method, which iteratively improves guesses for the square root of a number. This method is particularly useful for finding roots of numbers that are not perfect squares.
- Graphical Representation:
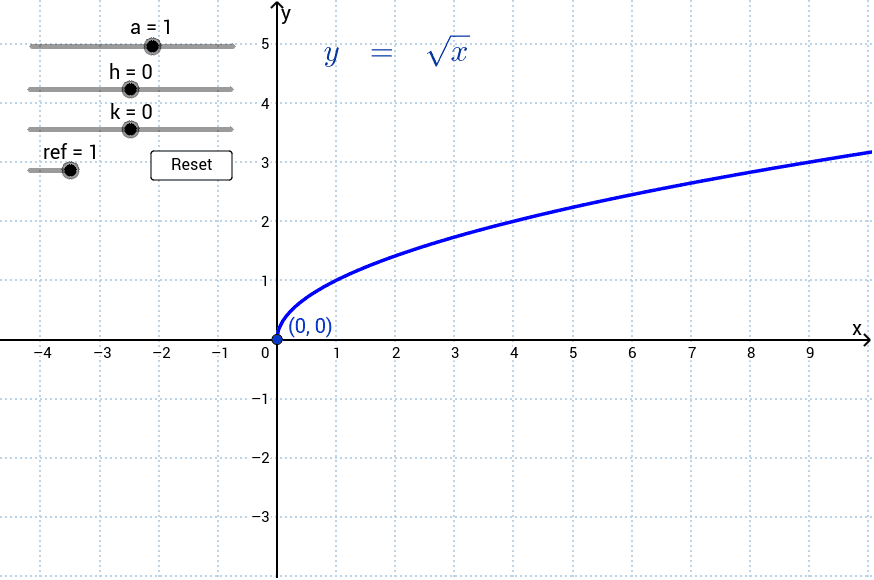
The function \( f(x) = \sqrt{x} \) can be graphed to show its behavior. The graph demonstrates that the square root function is increasing and concave down. As \( x \) increases, the rate of increase of \( \sqrt{x} \) decreases.

- Square Roots in Geometry:
In geometry, square roots are essential for calculating distances. For example, the distance formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \) derives from the Pythagorean theorem and requires finding the square root to determine the length of the hypotenuse in a right triangle.
- Prime Factorization:
Advanced techniques in number theory involve using prime factorization to simplify square roots. For example, \( \sqrt{28} = \sqrt{4 \cdot 7} = 2\sqrt{7} \), leveraging the property that the square root of a product is the product of the square roots.
Common Mistakes with Square Roots
Understanding square roots is fundamental in mathematics, but there are several common mistakes that students and even professionals can make. Recognizing these errors can help in avoiding them and ensuring accurate calculations.
-
Incorrect Simplification
A common mistake is assuming that the square root of a sum is the sum of the square roots, i.e., \( \sqrt{x + y} = \sqrt{x} + \sqrt{y} \). This is incorrect. For example:
\( \sqrt{9 + 16} \neq \sqrt{9} + \sqrt{16} \)
Instead, \( \sqrt{9 + 16} = \sqrt{25} = 5 \), whereas \( \sqrt{9} + \sqrt{16} = 3 + 4 = 7 \).
-
Square Root of a Square
Another frequent mistake is simplifying \( \sqrt{x^2} = x \). The correct simplification is \( \sqrt{x^2} = |x| \) because the square root function returns the non-negative value.
For example:
\( \sqrt{(-3)^2} = \sqrt{9} = 3 \), not -3.
-
Negative Numbers under Square Root
It's important to remember that the square root of a negative number is not a real number. For instance, \( \sqrt{-1} \) is not defined in the set of real numbers; it is defined as \( i \) in the set of complex numbers, where \( i \) is the imaginary unit.
-
Combining Square Roots Incorrectly
Students often make mistakes when adding or subtracting square roots that are not like terms. For example, \( 3\sqrt{2} + 4\sqrt{2} = 7\sqrt{2} \) is correct, but \( 3\sqrt{2} + 4\sqrt{3} \) cannot be simplified further because \( \sqrt{2} \) and \( \sqrt{3} \) are not like terms.
-
Misinterpretation of Squaring a Square Root
Another common error is misinterpreting the squaring of a square root. For example, \( (\sqrt{a})^2 = a \). However, students sometimes incorrectly assume \( (\sqrt{a})^2 = \sqrt{a^2} \).
The correct interpretation is:
\( (\sqrt{5})^2 = 5 \)
-
Rationalizing the Denominator Incorrectly
When rationalizing the denominator, ensure the correct process is followed. For instance, to rationalize \( \frac{1}{\sqrt{2}} \), multiply the numerator and the denominator by \( \sqrt{2} \):
\( \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \)
Practicing these concepts and being mindful of these common mistakes can help improve accuracy and understanding in handling square roots.
Practice Problems Involving 5 Square Root 7
Here are some practice problems to help you better understand and apply the concept of \( 5\sqrt{7} \):
- Calculate the approximate value of \( 5\sqrt{7} \).
- Solve for \( x \) in the equation \( 5\sqrt{7} = x \).
- Find the square of \( 5\sqrt{7} \).
- Determine the value of \( \frac{5}{\sqrt{7}} \).
- Express \( 5\sqrt{7} \) in decimal form.
- Verify whether \( 5\sqrt{7} \) is an irrational number.
- Compare \( 5\sqrt{7} \) with \( 10\sqrt{1.75} \).
Conclusion and Further Reading
In conclusion, exploring the mathematical concept of \( 5\sqrt{7} \) reveals its importance in various mathematical applications and problem-solving scenarios. It is an example of how square roots can be used to represent quantities in real-world contexts.
For further reading and practice, consider the following resources:
- Math textbooks covering topics on square roots and irrational numbers.
- Online math forums and communities for discussions and additional problem-solving.
- Mathematical websites offering interactive tools for calculating and understanding square roots.
- Advanced mathematical texts exploring deeper into the properties and applications of square roots.

Học về căn bậc hai và ứng dụng của chúng trong toán học với thầy J.
What are Square Roots? | Toán với thầy J
READ MORE:
Học cách đơn giản hóa căn bậc hai và áp dụng trong các bài toán toán học với hướng dẫn chi tiết và ví dụ minh họa.
Cách đơn giản hóa căn bậc hai | Hướng dẫn với ví dụ