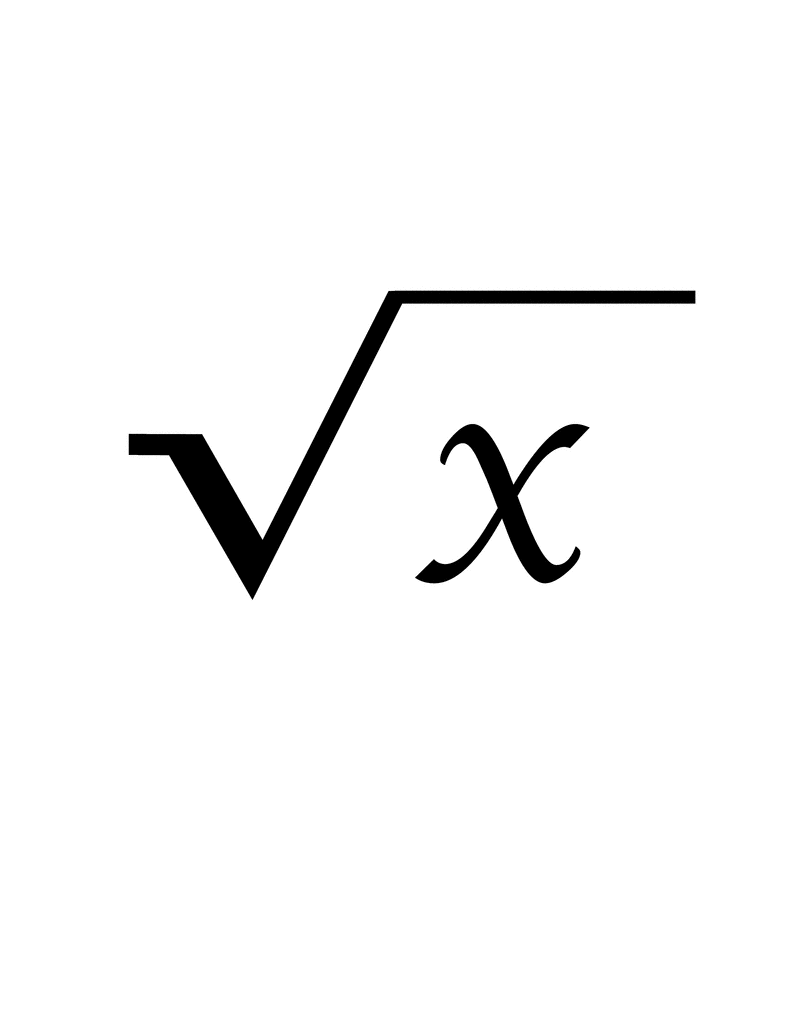Topic 1/2 square root: The square root of 1/2 can be simplified to 1/√2 and then rationalized to √2/2. This process involves breaking down the fraction under the square root and rationalizing the denominator. Understanding this concept helps in simplifying complex algebraic expressions and solving various mathematical problems effectively.
Table of Content
Understanding the Square Root of 1/2
The square root of 1/2, often represented as \( \sqrt{\frac{1}{2}} \), can be simplified and understood through various mathematical techniques. This concept is frequently explored in algebra and is crucial for students and professionals dealing with mathematical computations.
Step-by-Step Simplification
- Rewrite the expression: \[ \sqrt{\frac{1}{2}} = \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} \]
- Rationalize the denominator by multiplying the numerator and the denominator by \( \sqrt{2} \): \[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
Decimal Form
The decimal form of \( \frac{\sqrt{2}}{2} \) is approximately 0.7071.
Visual Representation
The square root of a number can also be represented visually. Calculators and online tools, such as , , and , provide step-by-step solutions and visual aids to help understand these calculations.
Applications
Understanding the square root of 1/2 is essential in various fields such as physics, engineering, and computer science, where precise calculations are required. The value is also crucial in statistical and geometrical problems where it frequently appears.
Additional Resources
These resources offer detailed explanations, example problems, and interactive calculators to further explore the square root of 1/2 and other mathematical concepts.

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations used to determine a number that, when multiplied by itself, yields the original number. This operation is symbolized by the radical sign (√). Understanding square roots is crucial in various mathematical contexts, including algebra, geometry, and calculus.
The square root of a number x is written as √x, and its value is the number that, when squared (multiplied by itself), equals x. For example, the square root of 25 is 5 because 5 × 5 = 25.
When dealing with fractions, the square root operation applies to both the numerator and the denominator separately. For instance, the square root of 1/2 can be simplified by taking the square root of 1 and the square root of 2 separately, resulting in √1/√2, which can be further simplified to √2/2.
In mathematical notation, this is expressed as:
\[
\sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
To rationalize the denominator, we multiply by the appropriate form of 1, which in this case is \(\frac{\sqrt{2}}{\sqrt{2}}\), leading to the simplified form \(\frac{\sqrt{2}}{2}\).
Square roots are not always whole numbers. For non-perfect squares, the result is an irrational number. For example, the square root of 2 is approximately 1.414, a non-terminating and non-repeating decimal.
Square roots are essential in solving quadratic equations and various algebraic expressions, making them a critical concept in higher-level mathematics.
Calculating the Square Root of 1/2
To calculate the square root of
-
Rewrite the expression under the square root:
\[ \sqrt{\frac{1}{2}} = \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} \] -
Simplify the expression further by calculating the square roots:
\[ \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} \] -
Rationalize the denominator to remove the square root from the denominator:
\[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \] -
The simplified form of the square root of
\(\frac{1}{2}\) is:\[ \sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2} \] -
In decimal form, this value is approximately:
\[ \frac{\sqrt{2}}{2} \approx 0.7071 \]
This process demonstrates how to handle square roots of fractions, particularly when the fraction is not a perfect square, by using rationalization techniques.
Simplifying Radicals
Simplifying radicals involves reducing the expression under the radical sign to its simplest form. This often includes rationalizing the denominator and combining like terms. Here, we focus on simplifying the square root of a fraction, such as 1/2.
To simplify the square root of 1/2, follow these steps:
- Rewrite the expression using the property of radicals:
- \(\sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}}\)
- Simplify the numerator and denominator separately:
- \(\sqrt{1} = 1\)
- \(\sqrt{2}\) remains as it is.
- Combine the results:
- \(\frac{1}{\sqrt{2}}\)
- Rationalize the denominator by multiplying both the numerator and the denominator by \(\sqrt{2}\):
- \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
The simplified form of \(\sqrt{\frac{1}{2}}\) is \(\frac{\sqrt{2}}{2}\).
For practical purposes, the decimal form of \(\frac{\sqrt{2}}{2}\) can be approximated as 0.7071.
Understanding these steps is crucial for simplifying more complex radical expressions and for performing various algebraic operations involving radicals.
Rationalizing the Denominator
Rationalizing the denominator involves eliminating any irrational numbers in the denominator of a fraction. This is done to make the expression easier to understand and work with. Below are steps to rationalize the denominator, with detailed explanations and examples.
- Identify the irrational denominator: Determine if the denominator is a single term or a binomial containing a radical.
- Multiply by the conjugate: For binomial denominators, use the conjugate. For example, the conjugate of \((a + \sqrt{b})\) is \((a - \sqrt{b})\).
- Multiply numerator and denominator: Multiply both the numerator and the denominator by the conjugate of the denominator.
- Simplify the expression: Perform the multiplication and combine like terms, then simplify the resulting fraction.
For example, to rationalize the denominator of \(\frac{1}{\sqrt{7}}\):
- Multiply by \(\frac{\sqrt{7}}{\sqrt{7}}\): \(\frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}} = \frac{\sqrt{7}}{7}\).
For a more complex example, rationalizing \(\frac{1}{5+\sqrt{2}}\):
- Multiply by the conjugate: \(\frac{1}{5+\sqrt{2}} \times \frac{5-\sqrt{2}}{5-\sqrt{2}} = \frac{5-\sqrt{2}}{25-2} = \frac{5-\sqrt{2}}{23}\).
Here are some additional tips for rationalizing the denominator:
- Ensure all radicals are simplified before starting the process.
- Combine like terms after multiplying.
- Always check to simplify the final fraction.

Decimal Approximation
Decimal approximation of square roots is a common technique used to estimate the value of a square root that does not result in an integer. This method provides a way to express square roots in a more manageable form for practical applications. Let's explore the steps involved in calculating the square root of 1/2 (0.5) and its decimal approximation.
First, we express the fraction 1/2 as a decimal: \(0.5\).
Next, we find the square root of 0.5. Using a calculator or the long division method, we determine that:
\[
\sqrt{0.5} \approx 0.7071
\]This value can be further approximated depending on the required precision. For example, to four decimal places, the square root of 0.5 is 0.7071.
Here is a detailed step-by-step explanation of the long division method to find the square root of 0.5:
Place a bar over every pair of digits starting from the decimal point: 0.50 | 00...
Start with the number under the first bar. Since we are dealing with 0.50, we consider 50.
The largest number whose square is less than or equal to 50 is 7 (since \(7^2 = 49\)). Write 7 above the bar as the first digit of the quotient.
Subtract \(49\) from \(50\) to get \(1\). Bring down the next pair of zeros to make it 100.
Double the number above the bar (7) and write it below as 14. Determine the largest digit (D) such that \(14D \times D \leq 100\). The appropriate digit here is 0, so we write 0 next to 14 and continue the process.
Bring down the next pair of zeros to make it 10000. Now, determine the largest digit (D) such that \(140D \times D \leq 10000\). This digit is 7 (since \(1407 \times 7 = 9849\)). Write 7 above as the next digit of the quotient and continue.
Continuing this process yields an increasingly precise approximation of the square root. Therefore, the square root of 0.5, when approximated to four decimal places, is 0.7071.
Square Root Calculators
Square root calculators are useful tools for quickly determining the square root of a number. They can handle both perfect squares and non-perfect squares, providing results in exact form and as decimal approximations. Here are some steps and features of square root calculators:
- Enter the Number: Input the number you want to find the square root of into the calculator.
- Choose Calculation Type: Some calculators allow you to select the type of calculation, such as finding the exact square root or the decimal approximation.
- View Results: The calculator will display the square root of the number, often in both exact and decimal forms.
Additional features of square root calculators include:
- Handling negative numbers and imaginary square roots.
- Simplifying radicals to their simplest form.
- Providing step-by-step solutions and explanations.
These tools are available online on websites like Mathway and Mathwarehouse, offering easy-to-use interfaces and additional mathematical resources for further learning and practice.
Applications of Square Roots
Square roots are fundamental in various fields, offering practical solutions and insights. Here are some notable applications:
- Geometry and Trigonometry: Square roots are crucial in calculating distances, areas, and volumes. For instance, in the Pythagorean theorem, the length of the hypotenuse is found using the square root of the sum of the squares of the other two sides.
- Physics: Square roots appear in various physical formulas, such as calculating the period of a pendulum or the root mean square speed of gas molecules, which involves taking the square root of the average of the squares of the velocities.
- Statistics: In statistics, the standard deviation, a measure of data dispersion, is derived using the square root of the variance. This helps in understanding the spread of data points in a dataset.
- Engineering: Engineers use square roots in various calculations, such as determining the stress and strain on materials. The square root function is also used in signal processing and electrical engineering.
- Computer Graphics: In computer graphics, square roots are used to calculate distances between points, which is essential for rendering images, animations, and 3D modeling.
- Finance: Square roots are used in financial calculations, including the determination of compound interest and the calculation of the volatility of stock prices.
- Medicine: In medicine, square roots are used in dosages and in understanding the spread of diseases. For example, the spread of epidemics can be modeled using equations involving square roots.
- Astronomy: Astronomers use square roots to calculate gravitational forces and distances between celestial objects, helping in understanding the universe's structure and behavior.
| Field | Application |
|---|---|
| Geometry | Calculating distances using the Pythagorean theorem. |
| Physics | Determining the period of a pendulum and root mean square speed of gas molecules. |
| Statistics | Finding the standard deviation to measure data dispersion. |
| Engineering | Calculating stress, strain, and signal processing. |
| Computer Graphics | Rendering images and 3D modeling. |
| Finance | Determining compound interest and stock price volatility. |
| Medicine | Calculating dosages and modeling disease spread. |
| Astronomy | Calculating gravitational forces and distances between celestial objects. |
Practice Problems and Solutions
Below are some practice problems related to square roots, along with detailed solutions to help you understand the process:
-
Problem 1: Find the square root of 1444 by the prime factorization method.
Solution:
- Prime factorization of 1444: \( 1444 = 2 \times 2 \times 19 \times 19 \)
- Making pairs of two: \( \sqrt{1444} = \sqrt{(2 \times 2) \times (19 \times 19)} \)
- Therefore, \( \sqrt{1444} = 2 \times 19 = 38 \)
-
Problem 2: Simplify \( \sqrt{\frac{1}{2}} \).
Solution:
- We know that \( \sqrt{\frac{1}{2}} = \frac{\sqrt{1}}{\sqrt{2}} = \frac{1}{\sqrt{2}} \)
- Rationalize the denominator: \( \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \)
- Thus, \( \sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2} \)
-
Problem 3: Calculate the square root of \( 25 + 20\sqrt{6} \).
Solution:
- Let \( x = \sqrt{25 + 20\sqrt{6}} \)
- Then, \( x^2 = 25 + 20\sqrt{6} \)
- Assume \( x = a + b\sqrt{6} \) and solve for \( a \) and \( b \).
- By comparing both sides, we get \( a = 5 \) and \( b = 2 \), so \( \sqrt{25 + 20\sqrt{6}} = 5 + 2\sqrt{6} \).
-
Problem 4: Find the square root of 0.25.
Solution:
- We know \( 0.25 = \frac{1}{4} \).
- Therefore, \( \sqrt{0.25} = \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2} \).
-
Problem 5: Verify if 1512 is a perfect cube. If not, find the smallest number to multiply it by to make it a perfect cube.
Solution:
- Prime factorization of 1512: \( 1512 = 2^3 \times 3^3 \times 7 \)
- Since 7 is not a cube, multiply by \( 7^2 = 49 \) to get \( 1512 \times 49 = 74088 \)
- The cube root of 74088 is \( \sqrt[3]{74088} = 42 \)
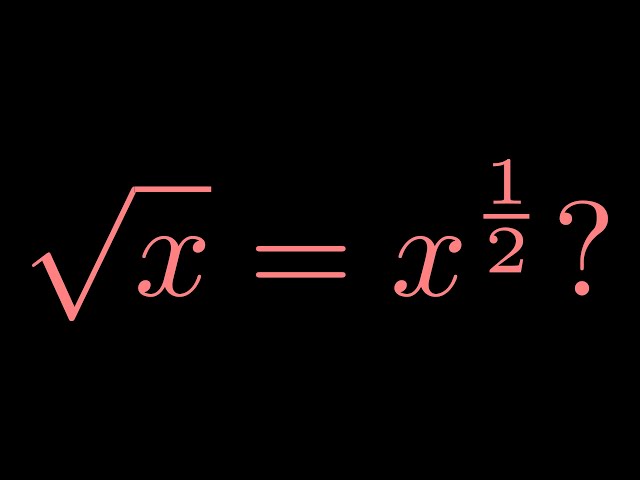
Tại sao căn bậc hai là lũy thừa 1/2
READ MORE:
Căn bậc hai của 2 + Căn bậc hai của 1/2 =? Nhiều người sẽ sai!