Topic what's the square root of 64: Are you curious about the square root of 64? This fundamental mathematical concept not only unveils an interesting number but also holds significance in various applications. Join us as we explore the square root of 64, how to calculate it, and its relevance in everyday life and advanced mathematical studies.
Table of Content
- Square Root of 64
- Introduction to Square Roots
- What is a Square Root?
- The Square Root of 64
- Calculation Methods for Square Roots
- Perfect Squares and Their Roots
- Why 64 is a Perfect Square
- Properties of the Square Root of 64
- Applications of Square Roots in Real Life
- Square Root of 64 in Mathematics
- Common Mistakes in Calculating Square Roots
- Advanced Square Root Concepts
- FAQs About Square Roots
- Conclusion
- YOUTUBE:
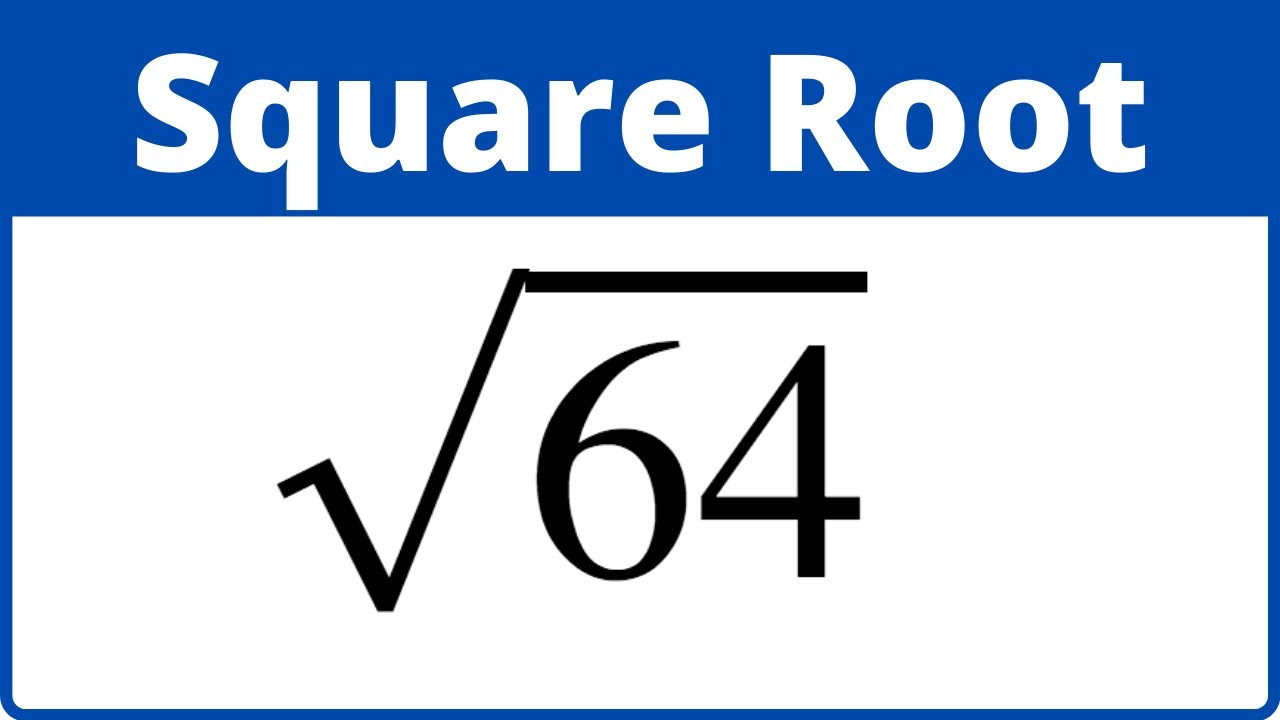
Square Root of 64
The square root of 64 is calculated as follows:
| Symbol | Value |
| √64 | 8 |
Therefore, the square root of 64 equals 8.

READ MORE:
Introduction to Square Roots
The concept of square roots is a fundamental element in mathematics, serving as the inverse operation to squaring a number. A square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). For instance, the square root of 64 is a number that, when multiplied by itself, equals 64.
Square roots can be both positive and negative because both \( 8 \times 8 \) and \( -8 \times -8 \) equal 64. Therefore, the square root of 64 is written as \( \pm 8 \). Understanding square roots involves several key steps and principles:
- Definition: The square root of a number \( x \) is a number \( y \) which satisfies the equation \( y^2 = x \).
- Symbol: The square root is denoted by the radical symbol \( \sqrt{} \). For example, the square root of 64 is written as \( \sqrt{64} \).
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For example, \( \sqrt{64} = 8 \) and \( \sqrt{64} = -8 \).
- Perfect Squares: Numbers like 64, which have integer square roots, are called perfect squares.
- Non-Perfect Squares: Numbers that do not have integer square roots are known as non-perfect squares and their square roots are irrational numbers.
Calculating square roots can be done using various methods:
- Prime Factorization: Break down the number into its prime factors. For 64, which is \( 2^6 \), the square root is \( 2^3 = 8 \).
- Estimation and Refinement: Estimate the square root and refine the estimate using methods such as averaging.
- Using a Calculator: Most calculators have a square root function that allows for quick computation.
Square roots play a crucial role in various fields, including algebra, geometry, and real-world applications like physics and engineering. They are essential for solving quadratic equations, working with right-angled triangles, and many other mathematical problems.
What is a Square Root?
A square root of a number is a value that, when multiplied by itself, gives the original number. It is one of the fundamental concepts in mathematics and has various applications in different fields.
Mathematically, the square root of a number x is denoted as \( \sqrt{x} \). For example, the square root of 64 is written as \( \sqrt{64} \).
The concept of square roots can be explained through the following steps:
- Identify the number for which you want to find the square root.
- Find a value that, when multiplied by itself, equals the original number.
In simpler terms, if \( y \times y = x \), then \( y \) is the square root of \( x \).
For example:
- \( 8 \times 8 = 64 \), so \( 8 \) is the square root of \( 64 \).
- \( 9 \times 9 = 81 \), so \( 9 \) is the square root of \( 81 \).
Square roots have the following properties:
- Every positive number has two square roots: one positive and one negative. For example, the square roots of 64 are \( 8 \) and \( -8 \).
- The square root of zero is zero.
- Negative numbers do not have real square roots because no real number squared gives a negative result.
Square roots are often used in various mathematical formulas and real-life applications, such as calculating areas, solving quadratic equations, and analyzing data.
Here is a table summarizing the square roots of some common perfect squares:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
The Square Root of 64
The square root of a number is a value that, when multiplied by itself, gives the original number. In the case of 64, its square root is 8, because \(8 \times 8 = 64\). This can be represented mathematically as:
\(\sqrt{64} = 8\)
However, every positive real number has two square roots: one positive and one negative. Therefore, the square roots of 64 are 8 and -8. This can be expressed as:
\(\pm \sqrt{64} = \pm 8\)
In most contexts, the positive square root is referred to as the principal square root. Thus, when we talk about "the square root of 64," we usually mean 8.
Methods to Calculate the Square Root of 64
There are several methods to determine the square root of a number. Here are a few commonly used methods:
1. Prime Factorization Method
Using the prime factorization method, we break down 64 into its prime factors:
- 64 = 2 × 2 × 2 × 2 × 2 × 2 = \(2^6\)
- \(\sqrt{64} = \sqrt{2^6} = 2^{6/2} = 2^3 = 8\)
2. Long Division Method
The long division method is another way to find the square root, especially useful for larger numbers or numbers that are not perfect squares. For 64, the process is straightforward:
- Pair the digits of the number from right to left.
- Find the largest number whose square is less than or equal to 64. This is 8, because \(8 \times 8 = 64\).
- Since 64 is a perfect square, the division process ends here with the result 8.
3. Repeated Subtraction Method
In the repeated subtraction method, we subtract successive odd numbers from 64 until we reach zero:
- 64 - 1 = 63
- 63 - 3 = 60
- 60 - 5 = 55
- 55 - 7 = 48
- 48 - 9 = 39
- 39 - 11 = 28
- 28 - 13 = 15
- 15 - 15 = 0
The number of subtractions is 8, which is the square root of 64.
Why 64 is a Perfect Square
A perfect square is a number that can be expressed as the product of an integer with itself. Since \(8 \times 8 = 64\), 64 is a perfect square. Additionally, 64 can be expressed as \(2^6\), which further confirms its status as a perfect square.
In conclusion, the square root of 64 is a fundamental concept in mathematics, illustrating the relationships between numbers and their roots. Understanding these methods allows for a deeper comprehension of square roots and their applications.
Calculation Methods for Square Roots
Calculating square roots can be approached through various methods, each suited for different situations. Below, we detail some of the most common and effective methods for finding square roots.
1. Prime Factorization Method
This method involves expressing the number as a product of prime factors and then simplifying:
- Step 1: Factorize the number into prime factors.
- Step 2: Pair the prime factors.
- Step 3: Take one factor from each pair.
For example, to find the square root of 64:
\[
64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = (2 \times 2 \times 2)^2 = 8^2
\]
Therefore, \(\sqrt{64} = 8\).
2. Long Division Method
This method is useful for finding square roots of non-perfect squares. Here’s how it works:
- Group the digits in pairs starting from the decimal point.
- Find the largest integer whose square is less than or equal to the first group.
- Subtract the square of this integer from the first group and bring down the next group of digits.
- Double the current result and use it as a new divisor, finding the next digit by trial and error.
Repeat the process to get more decimal places of the square root.
3. Newton-Raphson Method
Also known as the iterative method, this technique uses an initial guess and improves it iteratively:
- Step 1: Start with an initial guess \( x_0 \).
- Step 2: Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \).
- Step 3: Repeat until the desired precision is achieved.
For example, to find \(\sqrt{64}\) starting with \( x_0 = 8 \):
\[
x_{1} = \frac{1}{2} \left( 8 + \frac{64}{8} \right) = \frac{1}{2} \left( 8 + 8 \right) = 8
\]
Since \(8\) is already correct, the method converges immediately.
4. Using a Calculator
For quick and precise results, using a calculator is often the best choice. Most scientific calculators have a square root function. Simply input the number and press the square root button.
5. Estimation Techniques
When a rough estimate is sufficient, these techniques can be useful:
- Identify the nearest perfect squares around the number.
- Use these to approximate the square root.
For instance, to estimate \(\sqrt{50}\):
\[
49 < 50 < 64 \quad \text{so} \quad 7 < \sqrt{50} < 8
\]
These methods provide various ways to calculate square roots, each with its own advantages depending on the context and precision required.

Perfect Squares and Their Roots
A perfect square is a number that can be expressed as the product of an integer with itself. In other words, if \( n \) is an integer, then \( n^2 \) is a perfect square. Here is a detailed look at perfect squares and their roots:
- Definition: A perfect square is an integer that is the square of another integer. For example, 1, 4, 9, 16, and 25 are perfect squares because they can be written as \( 1^2, 2^2, 3^2, 4^2, \) and \( 5^2 \), respectively.
- Properties of Perfect Squares:
- Every perfect square has an odd number of total factors.
- The square root of a perfect square is always an integer.
- Examples of Perfect Squares:
Number Square Root 1 \(\sqrt{1} = 1\) 4 \(\sqrt{4} = 2\) 9 \(\sqrt{9} = 3\) 16 \(\sqrt{16} = 4\) 25 \(\sqrt{25} = 5\) 36 \(\sqrt{36} = 6\) 49 \(\sqrt{49} = 7\) 64 \(\sqrt{64} = 8\) 81 \(\sqrt{81} = 9\) 100 \(\sqrt{100} = 10\)
As we can see, the number 64 is a perfect square because it can be written as \( 8^2 \). Thus, the square root of 64 is 8. Perfect squares like these have many applications in mathematics and are foundational concepts for understanding more complex mathematical principles.
Why 64 is a Perfect Square
A perfect square is a number that can be expressed as the product of an integer with itself. In simpler terms, if you can find an integer that, when multiplied by itself, equals the original number, then that number is a perfect square.
For 64, the integer that satisfies this condition is 8, because:
\(8 \times 8 = 64\)
This relationship can also be expressed using exponents and radicals:
- Exponential form: \(64 = 8^2\)
- Radical form: \(\sqrt{64} = 8\)
There are several ways to verify that 64 is a perfect square:
- Multiplication Method: Recall basic multiplication facts. Knowing that \(8 \times 8 = 64\) quickly confirms that 64 is a perfect square.
- Prime Factorization: Break down 64 into its prime factors:
\(64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6\)
Pairing the prime factors, we get:\((2 \times 2) \times (2 \times 2) \times (2 \times 2) = 8\)
Therefore, \(\sqrt{64} = 8\). - Long Division Method: This systematic approach involves setting up the number under the square root sign, making an initial guess, and refining it through division steps. For 64, since \(8 \times 8 = 64\) with no remainder, it confirms that the square root is 8.
In conclusion, 64 is a perfect square because it is the product of the integer 8 multiplied by itself. This neat and tidy result, without fractions or decimals, makes it a perfect square.
Properties of the Square Root of 64
The square root of 64 has several interesting properties that make it a noteworthy number in mathematics. Here are some key properties:
-
Non-Negative Value:
The principal square root of 64 is non-negative. By definition, the square root function returns the non-negative root. Thus, \( \sqrt{64} = 8 \).
-
Perfect Square:
64 is a perfect square, meaning it is the square of an integer. Specifically, \( 64 = 8^2 \), so the square root of 64 is 8.
-
Real Number:
The square root of 64 is a real number. Since 64 is a positive number, its square root is also a positive real number.
-
Positive and Negative Roots:
While the principal square root of 64 is 8, it is important to note that both 8 and -8 squared give 64. Mathematically, \( 8^2 = 64 \) and \( (-8)^2 = 64 \). However, by convention, \( \sqrt{64} \) refers to the positive root only.
-
Product Property:
The square root of a product can be expressed as the product of the square roots. For example, \( \sqrt{64} = \sqrt{4 \times 16} = \sqrt{4} \times \sqrt{16} = 2 \times 4 = 8 \).
-
Square Root Function:
The function \( f(x) = \sqrt{x} \) is defined only for non-negative values of \( x \). It maps positive numbers to their principal square roots, making \( \sqrt{64} = 8 \) a point on this function's graph.
Understanding these properties helps in recognizing the consistent and unique characteristics of square roots, particularly for perfect squares like 64.
Applications of Square Roots in Real Life
Square roots are used in various real-life applications across different fields. Here are some key areas where square roots play an important role:
-
Geometry and Architecture:
Square roots are crucial in calculating distances, areas, and volumes. For example, the Pythagorean Theorem uses square roots to find the length of the hypotenuse of a right triangle, which is essential in construction and design.
-
Finance:
In finance, square roots are used to calculate stock market volatility. The volatility is determined by taking the square root of the variance of stock returns, helping investors understand the risk associated with investments.
-
Statistics:
Square roots are used to calculate standard deviation, a measure of the amount of variation or dispersion in a set of values. The standard deviation is the square root of the variance, which helps in data analysis and making informed decisions.
-
Physics and Engineering:
Square roots are used to calculate various physical properties. For instance, in physics, the speed of an object is often derived from equations involving square roots. In engineering, the natural frequency of structures is determined using square roots to ensure stability under different loads.
-
Computer Science:
In computer science, square roots are used in algorithms and computations. For example, in graphics programming, square roots are used to calculate distances between points, which is essential for rendering images and animations.
-
Navigation:
Pilots and navigators use square roots to calculate distances between points on a map. The distance formula, which involves square roots, helps in plotting accurate routes and ensuring safe travel.
-
Medicine:
In medical imaging, square roots are used in algorithms that process images from X-rays, CT scans, and MRIs. These calculations help in creating accurate images for diagnosis and treatment planning.
Overall, the applications of square roots are extensive and vital in various real-life scenarios, aiding in accurate calculations and informed decision-making.

Square Root of 64 in Mathematics
The square root of 64 is an important concept in mathematics with various properties and applications. Understanding the square root of 64 helps in solving equations, simplifying expressions, and understanding the nature of numbers.
Definition: The square root of a number is a value that, when multiplied by itself, gives the original number. For 64, the square root is:
\[ \sqrt{64} = 8 \]
Properties of the Square Root of 64
- Rational Number: The square root of 64 is 8, which is a rational number because it can be expressed as the fraction \(\frac{8}{1}\).
- Perfect Square: Since 64 is the product of an integer (8) multiplied by itself (8 × 8), it is considered a perfect square.
- Principal Square Root: The principal square root of 64 is 8, which is the non-negative root. Although \(-8\) is also a square root of 64, the principal (positive) square root is conventionally used.
Mathematical Representation
- Exponential Form: \[ 64^{\frac{1}{2}} \text{ or } 64^{0.5} \]
- Radical Form: \[ \sqrt{64} \]
Calculating the Square Root
There are several methods to calculate the square root of 64:
- Prime Factorization: Break down 64 into its prime factors: \(2 × 2 × 2 × 2 × 2 × 2 = 2^6\). Pair the factors and take one from each pair: \(2 × 2 × 2 = 8\).
- Basic Multiplication: Recognize that \(8 × 8 = 64\), hence, \(\sqrt{64} = 8\).
- Long Division Method: Though more complex, this method involves dividing 64 into pairs of digits and iteratively finding the quotient.
Significance in Equations
The square root function is essential in solving quadratic equations. For instance, to solve \(x^2 = 64\), we find:
\[ x = \pm \sqrt{64} \]
This yields two solutions: \(x = 8\) and \(x = -8\).
Use in Simplifying Expressions
Square roots are used to simplify expressions involving squares. For example:
\[ \sqrt{a^2} = a \text{ if } a \ge 0 \]
For \(a = 8\), \(\sqrt{8^2} = 8\).
Understanding the square root of 64 aids in comprehending more complex mathematical concepts and is a fundamental element in algebra and number theory.
Common Mistakes in Calculating Square Roots
Calculating square roots can be tricky, and several common mistakes often arise. Being aware of these can help in avoiding them and ensuring accurate calculations.
-
Mistake: Incorrect Simplification
One common error is incorrect simplification. For example, assuming that \( \sqrt{x + y} = \sqrt{x} + \sqrt{y} \) is incorrect. Instead, remember that \( \sqrt{x + y} \neq \sqrt{x} + \sqrt{y} \).
-
Mistake: Incorrect Addition
Another frequent mistake is adding square roots incorrectly. For example, \( 3\sqrt{5} + 2\sqrt{5} \) should be correctly simplified to \( 5\sqrt{5} \), not \( 6\sqrt{5} \).
-
Mistake: Squaring Fractions
Squaring fractions can lead to errors. For instance, \( (0.2)^2 \) should be \( 0.04 \), not \( 0.4 \). The correct calculation is \( 0.2 \times 0.2 = 0.04 \).
-
Mistake: Negative Squared Values
Squaring negative values correctly is crucial. For example, \( (-3)^2 \) is \( 9 \), not \( -9 \). The proper calculation is \( (-3) \times (-3) = 9 \).
-
Mistake: Incorrect Multiplication
Misapplying multiplication rules can cause mistakes, such as assuming \( (4a)^2 = 4a^2 \). The correct calculation is \( (4a)^2 = 16a^2 \).
-
Mistake: Misinterpreting Decimals
Decimals can be tricky; for instance, \( \sqrt{0.9} \) is not \( 0.3 \). Instead, properly simplify and calculate to avoid errors.
-
Mistake: Square Roots of Non-Perfect Squares
Approximating the square roots of non-perfect squares can lead to mistakes. For example, correctly identifying the nearest perfect squares and using methods like averaging can improve accuracy.
To avoid these mistakes, it is important to practice regularly and understand the underlying concepts thoroughly. Ensuring accurate calculations helps build a strong foundation in mathematics.
Advanced Square Root Concepts
Advanced concepts in square roots go beyond the basic understanding of finding the square root of a number. These concepts include properties, applications in complex numbers, and the relationship with other mathematical operations.
Properties of Square Roots
- Product Property: The square root of a product is equal to the product of the square roots of the factors:
\(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Power Property: The square root of a number raised to a power is equal to the number raised to half that power:
\(\sqrt{a^n} = a^{\frac{n}{2}}\)
Square Roots of Negative and Complex Numbers
For negative numbers, the square root involves imaginary numbers. The square root of -1 is represented as \(i\), where \(i\) is the imaginary unit:
\(\sqrt{-a} = i \cdot \sqrt{a}\)
Complex numbers extend this concept. For example, the square root of a complex number \(a + bi\) can be found using specific algebraic methods to determine its real and imaginary parts.
Square Roots in Calculus
In calculus, square roots are used in various contexts such as solving differential equations, integrating functions involving roots, and understanding the behavior of functions at their critical points. For instance, the derivative of the square root function is given by:
\(\frac{d}{dx} \sqrt{x} = \frac{1}{2\sqrt{x}}\)
Application in Geometry
Square roots are fundamental in geometry, particularly in the Pythagorean theorem, which relates the lengths of the sides of a right triangle:
\(c = \sqrt{a^2 + b^2}\)
Here, \(c\) is the hypotenuse, and \(a\) and \(b\) are the other two sides of the triangle.
Square Roots in Real-World Problems
Square roots are used in various real-world applications such as calculating distances, understanding wave functions in physics, and analyzing statistical data through standard deviation.
Understanding these advanced concepts of square roots enhances problem-solving skills and broadens the application of mathematical principles in various fields.
FAQs About Square Roots
Square roots can be a confusing topic for many. Here, we address some of the most frequently asked questions to help clarify any doubts you might have.
- What is the square root of 64?
The square root of 64 is \( \sqrt{64} = 8 \). This is because \( 8 \times 8 = 64 \).
- What are square roots?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \( 5 \times 5 = 25 \).
- How do you calculate square roots?
Square roots can be calculated using various methods, such as:
- Prime factorization
- Using a calculator
- Long division method
- Why is 64 a perfect square?
A perfect square is a number that is the square of an integer. Since \( 8 \times 8 = 64 \), 64 is a perfect square.
- Can square roots be negative?
While the principal square root of a positive number is positive, every positive number actually has two square roots: one positive and one negative. For example, \( \sqrt{64} = 8 \) and \( -\sqrt{64} = -8 \).
- What are some properties of square roots?
Some properties of square roots include:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) for \( b \neq 0 \)
- \( (\sqrt{a})^2 = a \)
- Are there square roots of negative numbers?
The square root of a negative number is not a real number. Instead, it is an imaginary number. For example, \( \sqrt{-64} = 8i \), where \( i \) is the imaginary unit and \( i^2 = -1 \).
- What is the symbol for square root?
The symbol for the square root is \( \sqrt{} \). For example, the square root of 9 is written as \( \sqrt{9} \).
- What are perfect squares?
Perfect squares are numbers that are the square of an integer. Examples include 1, 4, 9, 16, 25, 36, 49, 64, and so on.
- Can you estimate square roots?
Yes, you can estimate square roots by finding the two closest perfect squares the number falls between and estimating accordingly. For example, \( \sqrt{50} \) is between \( \sqrt{49} = 7 \) and \( \sqrt{64} = 8 \).
Conclusion
The square root of 64 is a fundamental concept in mathematics that illustrates the process of finding a number which, when multiplied by itself, equals 64. This number is 8, making the square root of 64 both straightforward and significant in understanding the properties of perfect squares.
Throughout this article, we have explored various aspects of square roots, focusing particularly on the square root of 64. We started by defining what a square root is and explained that the square root of 64 is 8 because 8 multiplied by itself gives 64 (8 × 8 = 64). We also covered methods to calculate square roots, such as the repeated subtraction method, prime factorization, and long division, demonstrating the different ways to arrive at the same result.
Understanding perfect squares and their roots helps in simplifying many mathematical problems and concepts. Recognizing that 64 is a perfect square and knowing its square root (8) can be useful in various mathematical applications, from algebra to geometry.
In addition to the mathematical significance, square roots have practical applications in real life, such as in physics, engineering, and computer science. They are used in calculations involving areas, volumes, and other measurements, where the understanding of root values simplifies complex equations.
In summary, the square root of 64 exemplifies how fundamental mathematical principles can be applied to solve problems and understand larger concepts. By mastering square roots, students and professionals can enhance their problem-solving skills and apply these concepts in various fields.
Square Root of 64
READ MORE:
Cách Tính Căn Bậc Hai của 64: Sqrt(64)