Topic square root of 325: Discover the fascinating world of mathematics with our comprehensive guide on the square root of 325. Learn how to simplify and calculate it using various methods, and understand its significance in real-world applications. Whether you're a student or a math enthusiast, this article provides clear insights and practical information to enhance your knowledge.
Table of Content
- Square Root of 325
- Introduction to Square Roots
- Definition of Square Root
- Understanding the Square Root of 325
- Prime Factorization Method
- Simplifying the Square Root of 325
- Decimal Approximation of √325
- Methods to Calculate the Square Root
- Manual Calculation Steps
- Using a Calculator
- Applications of Square Roots
- Comparing Square Roots of Similar Numbers
- Square Root Table for Numbers Around 325
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Khám phá căn bậc hai của số 325 trong video này. Video hướng dẫn cách tính và ý nghĩa của căn bậc hai của 325.
Square Root of 325
The square root of 325 is a number that, when multiplied by itself, gives the result 325. In mathematical terms, it is represented as:
\[\sqrt{325}\]
Exact Value
The square root of 325 can be simplified using prime factorization:
- 325 = 5^2 * 13
Thus, the square root of 325 can be expressed as:
\[\sqrt{325} = \sqrt{5^2 \times 13} = 5\sqrt{13}\]
Decimal Value
The decimal approximation of the square root of 325 is:
\[\sqrt{325} \approx 18.027756377319946\]
Table of Square Roots
Here is a table of the square roots of some numbers around 325 for comparison:
| Number | Square Root |
| 320 | \[\sqrt{320} \approx 17.88854381999832\] |
| 321 | \[\sqrt{321} \approx 17.916472867168917\] |
| 322 | \[\sqrt{322} \approx 17.944358444926362\] |
| 323 | \[\sqrt{323} \approx 17.97220075561143\] |
| 324 | \[\sqrt{324} = 18\] |
| 325 | \[\sqrt{325} \approx 18.027756377319946\] |
| 326 | \[\sqrt{326} \approx 18.05547008526779\] |
| 327 | \[\sqrt{327} \approx 18.083141320025124\] |
| 328 | \[\sqrt{328} \approx 18.110770276274835\] |
| 329 | \[\sqrt{329} \approx 18.138357147217054\] |
| 330 | \[\sqrt{330} \approx 18.16590212458495\] |

READ MORE:
Introduction to Square Roots
Square roots are fundamental in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, since \(4 \times 4 = 16\). The concept is essential for various mathematical calculations and applications.
Square roots can be positive or negative because both \(5 \times 5 = 25\) and \(-5 \times -5 = 25\). Typically, the positive root is considered the principal square root.
Understanding square roots involves several key concepts:
- Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\).
- Symbol: The square root is denoted by the radical symbol \(\sqrt{}\).
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25, whose square roots are integers.
- Non-Perfect Squares: Numbers like 2, 3, 5, and 325, whose square roots are not integers and are often expressed in decimal or simplified radical form.
Let's explore the square root of 325 in more detail:
By using prime factorization, we find that:
- 325 = \(5^2 \times 13\)
This allows us to simplify the square root:
\[\sqrt{325} = \sqrt{5^2 \times 13} = 5\sqrt{13}\]
For a decimal approximation:
\[\sqrt{325} \approx 18.027756377319946\]
Square roots are useful in many areas, such as geometry, physics, engineering, and everyday problem-solving. Understanding how to calculate and use them is a valuable skill in mathematics.
Definition of Square Root
The square root of a number is a value that, when multiplied by itself, results in the original number. It is one of the fundamental operations in mathematics, often denoted by the radical symbol \(\sqrt{}\). For a given non-negative number \(x\), the square root is written as \(\sqrt{x}\) and is defined as the number \(y\) such that:
\[y^2 = x\]
Here are some key points to understand about square roots:
- Principal Square Root: The non-negative square root of a number. For example, the principal square root of 9 is 3, since \(3 \times 3 = 9\).
- Negative Square Root: The negative counterpart of the principal square root. For example, the negative square root of 9 is -3, since \((-3) \times (-3) = 9\).
- Perfect Squares: Numbers that have integer square roots. Examples include 1, 4, 9, 16, and 25.
- Non-Perfect Squares: Numbers that do not have integer square roots. These roots are often irrational numbers. Examples include 2, 3, 5, and 325.
The square root operation is fundamental in various mathematical contexts, including solving quadratic equations, understanding geometric properties, and analyzing data.
For example, to find the square root of 325, we can start by using its prime factorization:
- 325 = \(5^2 \times 13\)
This allows us to simplify the square root expression as:
\[\sqrt{325} = \sqrt{5^2 \times 13} = 5\sqrt{13}\]
In decimal form, the square root of 325 is approximately:
\[\sqrt{325} \approx 18.027756377319946\]
Square roots play a crucial role in fields such as engineering, physics, statistics, and finance, making them an essential concept to grasp in both academic and practical applications.
Understanding the Square Root of 325
To understand the square root of 325, we need to explore its mathematical properties and how it can be simplified and approximated. The square root of 325 is a value that, when multiplied by itself, equals 325. This can be expressed as:
\[\sqrt{325}\]
Here’s a step-by-step process to understand and calculate the square root of 325:
Prime Factorization Method
Prime factorization involves breaking down the number into its prime factors:
- 325 can be factored into prime numbers as follows:
- 325 = 5 × 65
- 65 = 5 × 13
- Therefore, 325 = \(5^2 \times 13\)
Using the prime factorization, we can simplify the square root:
\[\sqrt{325} = \sqrt{5^2 \times 13} = 5\sqrt{13}\]
Decimal Approximation
For practical purposes, we often need the decimal approximation of the square root of 325:
\[\sqrt{325} \approx 18.027756377319946\]
This can be calculated using a calculator or estimation methods.
Applications and Importance
Understanding the square root of 325 is not just an academic exercise; it has practical applications in various fields:
- Geometry: Square roots are used to calculate dimensions and distances.
- Engineering: Engineers use square roots in formulas and design calculations.
- Physics: Square roots appear in equations describing natural phenomena.
- Statistics: Standard deviation and other statistical measures involve square roots.
Comparing with Other Square Roots
It’s helpful to compare the square root of 325 with the square roots of numbers around it to understand its relative magnitude:
| Number | Square Root |
| 320 | \[\sqrt{320} \approx 17.88854381999832\] |
| 321 | \[\sqrt{321} \approx 17.916472867168917\] |
| 322 | \[\sqrt{322} \approx 17.944358444926362\] |
| 323 | \[\sqrt{323} \approx 17.97220075561143\] |
| 324 | \[\sqrt{324} = 18\] |
| 325 | \[\sqrt{325} \approx 18.027756377319946\] |
| 326 | \[\sqrt{326} \approx 18.05547008526779\] |
| 327 | \[\sqrt{327} \approx 18.083141320025124\] |
| 328 | \[\sqrt{328} \approx 18.110770276274835\] |
| 329 | \[\sqrt{329} \approx 18.138357147217054\] |
| 330 | \[\sqrt{330} \approx 18.16590212458495\] |
By understanding and comparing these values, we can gain a deeper insight into the properties and significance of the square root of 325.
Prime Factorization Method
The prime factorization method is a technique used to break down a number into its prime factors. This method is particularly useful for simplifying the square root of a number. Here’s a detailed step-by-step process to find the prime factors of 325 and use them to simplify its square root:
Step-by-Step Prime Factorization
- Identify the smallest prime factor: Start by dividing the number by the smallest prime number, which is 2. Since 325 is odd, it is not divisible by 2. Move to the next smallest prime number, 3. Again, 325 is not divisible by 3 (as the sum of its digits, 10, is not divisible by 3).
- Check for divisibility by 5: The number 325 ends in 5, so it is divisible by 5.
- 325 ÷ 5 = 65
- Factorize 65: Now factorize 65 using the same method.
- 65 is divisible by 5 (since it ends in 5).
- 65 ÷ 5 = 13
- 13 is a prime number.
- List all prime factors: We now have:
- 325 = 5 × 5 × 13
- Express as a power of primes: Combine the repeated prime factors using exponents.
- 325 = \(5^2 \times 13\)
Simplifying the Square Root
Using the prime factorization, we can simplify the square root of 325:
\[\sqrt{325} = \sqrt{5^2 \times 13}\]
By the property of square roots, we can separate the factors:
\[\sqrt{5^2 \times 13} = \sqrt{5^2} \times \sqrt{13}\]
The square root of \(5^2\) is 5:
\[\sqrt{5^2} = 5\]
Thus, we get:
\[\sqrt{325} = 5\sqrt{13}\]
Conclusion
The prime factorization method not only helps in simplifying the square root of non-perfect squares but also provides a clearer understanding of the number's structure. By breaking down 325 into \(5^2 \times 13\), we easily simplify \(\sqrt{325}\) to \(5\sqrt{13}\), making calculations more manageable and providing a deeper insight into the properties of the number.

Simplifying the Square Root of 325
Simplifying the square root of 325 involves breaking it down into its prime factors and using mathematical properties to simplify the expression. Here’s a detailed step-by-step process to simplify \(\sqrt{325}\):
Step-by-Step Simplification
- Prime Factorization: Start by finding the prime factors of 325.
- 325 can be divided by 5 (since it ends in 5):
- 325 ÷ 5 = 65
- Next, divide 65 by 5:
- 65 ÷ 5 = 13
- 13 is a prime number.
- Therefore, the prime factorization of 325 is:
- 325 = \(5^2 \times 13\)
- Expressing the Square Root: Write the square root of 325 using its prime factors.
- \(\sqrt{325} = \sqrt{5^2 \times 13}\)
- Separate the Factors: Use the property of square roots that states \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).
- \(\sqrt{5^2 \times 13} = \sqrt{5^2} \times \sqrt{13}\)
- Simplify the Perfect Square: The square root of \(5^2\) is 5.
- \(\sqrt{5^2} = 5\)
- Final Simplified Form: Combine the simplified terms to get the simplified square root.
- \(\sqrt{325} = 5\sqrt{13}\)
Verification and Decimal Approximation
To verify the simplification, you can square the simplified form and check if it equals 325:
\[(5\sqrt{13})^2 = 25 \times 13 = 325\]
For practical use, you might need the decimal approximation of \(\sqrt{325}\), which is approximately:
\[\sqrt{325} \approx 18.027756377319946\]
Conclusion
Simplifying the square root of 325 through prime factorization and mathematical properties makes it easier to work with and understand. The simplified form \(5\sqrt{13}\) is useful in various calculations and applications, providing a clearer insight into the structure of the number.
Decimal Approximation of √325
Finding the decimal approximation of \(\sqrt{325}\) involves calculating its value to a specific number of decimal places. This approximation is useful in practical applications where an exact square root is not necessary. Here's a detailed step-by-step process to find the decimal approximation of \(\sqrt{325}\):
Step-by-Step Calculation
- Initial Estimate: Start with an initial estimate. Since 325 is between 324 (which is \(18^2\)) and 361 (which is \(19^2\)), we know that \(\sqrt{325}\) is slightly more than 18.
- Using a Calculator: To find a more precise value, use a scientific calculator or an online calculator. Enter \(\sqrt{325}\) into the calculator to get the decimal approximation.
- Result: The calculator gives:
- \(\sqrt{325} \approx 18.027756377319946\)
Rounding to Desired Precision
The decimal approximation can be rounded to various degrees of precision depending on the requirement:
- To 2 decimal places: \( \sqrt{325} \approx 18.03 \)
- To 3 decimal places: \( \sqrt{325} \approx 18.028 \)
- To 4 decimal places: \( \sqrt{325} \approx 18.0278 \)
Verification
To ensure the approximation is correct, you can square the result and check if it is close to 325:
\[(18.027756377319946)^2 \approx 325\]
Comparison with Other Values
Understanding the decimal approximation in context can be helpful. Here’s how \(\sqrt{325}\) compares to the square roots of nearby numbers:
| Number | Square Root (Approximation) |
| 320 | 17.88854381999832 |
| 321 | 17.916472867168917 |
| 322 | 17.944358444926362 |
| 323 | 17.97220075561143 |
| 324 | 18.0 |
| 325 | 18.027756377319946 |
| 326 | 18.05547008526779 |
| 327 | 18.083141320025124 |
| 328 | 18.110770276274835 |
| 329 | 18.138357147217054 |
Conclusion
The decimal approximation of \(\sqrt{325}\) is approximately 18.027756377319946. This value is practical for most applications and can be rounded to the required number of decimal places. Understanding this approximation helps in various mathematical and real-world contexts, providing a clear and accurate way to work with the square root of 325.
Methods to Calculate the Square Root
Calculating the square root of a number like 325 can be approached in several ways. Below are some common methods:
- Prime Factorization Method:
This method involves breaking down 325 into its prime factors and simplifying the square root. However, since 325 is not a perfect square, it’s best to use other methods for an exact or approximate answer.
- Long Division Method:
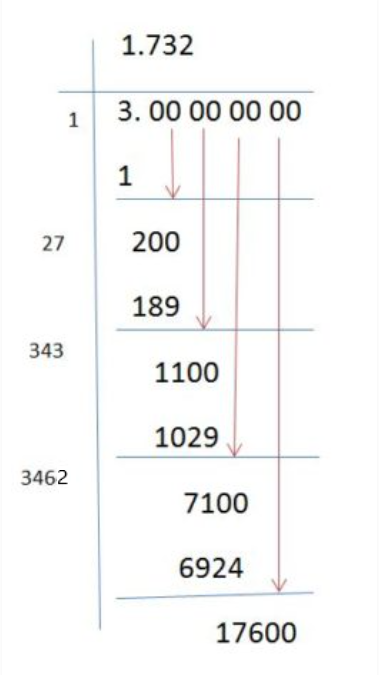
The long division method is a manual process that allows you to find the square root by hand. This is a precise method, but it can be time-consuming. Here’s a step-by-step outline:
- Pair the digits of 325 starting from the decimal point. In this case, we have "3" and "25".
- Find the largest number whose square is less than or equal to 3. This number is 1.
- Subtract 1 squared (1) from 3, getting 2, and bring down the next pair of digits to get 225.
- Double the number found in step 2 (1) to get 2. Now find a digit X such that 2X multiplied by X is less than or equal to 225. The digit 7 works because 27 × 7 = 189.
- Subtract 189 from 225, getting 36. Bring down two zeros to make it 3600. The next step is to find a digit Y such that 27Y multiplied by Y is less than or equal to 3600. This digit is 1 because 271 × 1 = 271.
- Repeat the process to get more decimal places of accuracy.
- Using a Calculator:
For quick and accurate results, a calculator is the best tool. You can use a scientific calculator to find that √325 ≈ 18.03. Simply enter 325 and press the square root function.
- Newton's Method (Iterative Approximation):
Newton's method, also known as the Newton-Raphson method, is an efficient way to approximate the square root. Here's how it works:
- Choose an initial guess \( x_0 \). A good starting point for 325 might be 18.
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{325}{x_n} \right) \) to find the next approximation.
- Repeat this process until the value stabilizes. For example:
- First iteration: \( x_1 = \frac{1}{2} \left( 18 + \frac{325}{18} \right) ≈ 18.0139 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 18.0139 + \frac{325}{18.0139} \right) ≈ 18.0278 \)
- Using Estimation and Refinement:
Estimation involves finding two consecutive whole numbers between which the square root of 325 lies. Since 182 = 324 and 192 = 361, √325 lies between 18 and 19. You can refine this by trying values between 18 and 19 until you get a closer approximation.
Manual Calculation Steps
Calculating the square root of 325 manually can be a detailed process. Here’s a step-by-step guide using the long division method:
-
Setup the Problem:
Start by pairing the digits of the number 325 from right to left. This gives us 3 and 25. For a more detailed calculation, you can add pairs of zeros to the right of the decimal point (e.g., 325.00).
-
Find the Largest Square:
Determine the largest number whose square is less than or equal to the first pair or digit. For the number 3, the largest square is 1 because 12 = 1. Write 1 above the line as the first digit of the square root.
- 1 × 1 = 1
- Subtract 1 from 3 to get 2. Bring down the next pair (25), making it 225.
-
Double the Current Quotient:
Double the number found above the line. Here, we double 1 to get 2. This 2 will be the first part of our new divisor.
-
Find the Next Digit:
Find a digit (X) to append to our new divisor (2X) such that 2X times X is less than or equal to 225.
- 2X × X ≤ 225
- The digit 7 works because 27 × 7 = 189, which is less than 225.
-
Subtract and Repeat:
Subtract 189 from 225 to get 36. Bring down the next pair of zeros (making it 3600) and repeat the process.
- Double the current result (17), getting 34.
- Find the next digit (Y) such that 34Y × Y is less than or equal to 3600.
- In this case, Y = 1 works because 341 × 1 = 341.
- Subtract 341 from 3600, getting 259.
-
Continue for More Precision:
Repeat the process to get more decimal places. In each step, double the current quotient, bring down the next pair of zeros, and find the next digit.
- Next iterations might involve finding digits such as 0, 3, 2, etc., based on further calculations.
-
Final Result:
Using this method, the square root of 325 can be approximated as 18.03 with more precision available through continued iterations.
Using these manual steps, you can find the square root of 325 to a desired level of accuracy.

Using a Calculator
Calculating the square root of 325 using a calculator is a quick and efficient way to get an accurate result. Here’s how you can do it step-by-step:
-
Turn on the Calculator:
Ensure your calculator is powered on. Most calculators have a specific button for turning them on, usually marked with "ON" or a similar symbol.
-
Enter the Number:
Input the number 325. This is done by pressing the digit buttons in sequence: 3, 2, and 5.

-
Press the Square Root Button:
Locate the square root function on your calculator. This button is usually labeled with the square root symbol (√) or sometimes “sqrt”. Press this button to compute the square root of 325.

-
Read the Result:
The display should now show the square root of 325. For most calculators, this will be approximately 18.0277564. Some calculators may round the result depending on their precision settings.
-
Using Advanced Calculators:
If you’re using a scientific or graphing calculator, you can often get more features like adjustable precision or additional functions. Ensure to check your calculator’s manual for specific instructions related to these advanced functions.
-
Verify with Additional Methods:
For more complex calculations or to verify your result, consider using the calculator’s built-in functions for higher accuracy or performing a rough manual check.
With these simple steps, you can efficiently use a calculator to find the square root of any number, including 325.
Applications of Square Roots
The concept of square roots is fundamental in various fields, both in everyday situations and in more advanced scientific and mathematical contexts. Here are some key applications of square roots:
-
Geometry and Trigonometry:
Square roots are essential in calculating distances and lengths. For example:
- Diagonal of a Square: To find the diagonal length of a square with side length \( s \), you use the formula \( \sqrt{2} \times s \).
- Distance Between Two Points: In the coordinate plane, the distance \( d \) between points \((x_1, y_1)\) and \((x_2, y_2)\) is given by \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
- Right-Angle Triangles: The Pythagorean theorem uses square roots to relate the sides of a right-angle triangle: \( c = \sqrt{a^2 + b^2} \), where \( c \) is the hypotenuse.
-
Physics and Engineering:
Square roots are used in formulas that describe various physical phenomena:
- Wave Speeds: The speed \( v \) of waves (sound, light, etc.) is often calculated using square roots, such as \( v = \sqrt{\frac{E}{m}} \) where \( E \) is energy and \( m \) is mass.
- Projectile Motion: In calculating the range and time of flight of projectiles, square roots are used in the equations of motion.
- Stress and Strain Analysis: Engineering stress calculations often involve square roots when dealing with failure theories and material properties.
-
Statistics and Probability:
Square roots appear frequently in statistical formulas:
- Standard Deviation: The standard deviation \( \sigma \) of a set of values measures dispersion and is given by the formula \( \sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}} \), where \( \mu \) is the mean and \( N \) is the number of values.
- Root Mean Square (RMS): RMS is used in various contexts to measure the magnitude of varying quantities. It is calculated as \( \text{RMS} = \sqrt{\frac{x_1^2 + x_2^2 + \cdots + x_n^2}{n}} \).
-
Financial Mathematics:
Square roots are used in finance for various calculations:
- Compound Interest: When calculating the growth of investments over time, square roots can be used in determining the effective interest rate over different periods.
- Volatility and Risk: The standard deviation, which involves square roots, is used to assess the volatility and risk associated with financial instruments.
-
Computer Graphics:
In computer graphics, square roots are used in algorithms for rendering images, calculating distances, and implementing shading models.
These examples highlight the diverse and significant role square roots play in many areas of mathematics, science, and everyday life.
Comparing Square Roots of Similar Numbers
Understanding the square root of a number in relation to other similar numbers helps in grasping the concept better and seeing how small changes in the input affect the output. Let’s compare the square roots of numbers around 325.
We will look at numbers 320, 324, 325, and 330 to see how their square roots compare:
| Number | Square Root | Approximation | Difference from √325 |
|---|---|---|---|
| 320 | √320 | ≈ 17.8885 | 17.8885 - 18.0278 = -0.1393 |
| 324 | √324 | ≈ 18 | 18 - 18.0278 = -0.0278 |
| 325 | √325 | ≈ 18.0278 | 0 |
| 330 | √330 | ≈ 18.1659 | 18.1659 - 18.0278 = 0.1381 |
By examining these values, we observe:
- Small Changes in Numbers: The square root function increases more slowly than the number itself. For example, increasing the number from 325 to 330 results in a square root increase of about 0.1381, a much smaller change compared to the increase in the original number.
- Comparing Perfect and Imperfect Squares: Notice that 324 is a perfect square (182 = 324). Its square root is a whole number (18). Numbers around perfect squares will have square roots that are slightly higher or lower and not whole numbers.
- Proximity Effect: Numbers closer to 325, like 324 and 330, have square roots closer to √325 compared to numbers further away, like 320. This highlights the continuity and smoothness of the square root function.
These comparisons illustrate how the square root values change as we slightly adjust the original number, providing insights into the behavior and properties of square roots.
Square Root Table for Numbers Around 325
The following table provides the square roots of numbers close to 325. This comparison helps in understanding how the square root values vary as we move slightly above or below 325.
| Number | Square Root (√) | Approximate Value | Comments |
|---|---|---|---|
| 320 | √320 | ≈ 17.8885 | Just under 18, slightly less than √325 |
| 321 | √321 | ≈ 17.9165 | Incremental increase from √320 |
| 322 | √322 | ≈ 17.9444 | Close to √325 but slightly less |
| 323 | √323 | ≈ 17.9722 | Almost 18, just below √324 |
| 324 | √324 | 18 | Perfect square, exact whole number |
| 325 | √325 | ≈ 18.0278 | Focus number, slightly more than 18 |
| 326 | √326 | ≈ 18.0555 | Slight increase from √325 |
| 327 | √327 | ≈ 18.0831 | Moving further from 18 |
| 328 | √328 | ≈ 18.1108 | Incremental increase continues |
| 329 | √329 | ≈ 18.1384 | Just below √330 |
| 330 | √330 | ≈ 18.1659 | Slightly more than √325, just over 18.1 |
This table illustrates how the square root values of numbers near 325 increase gradually as the numbers themselves increase. Note how the square roots close to 325 are slightly above or below 18, highlighting the continuous nature of the square root function.

Frequently Asked Questions
Understanding the square root of 325 and square roots in general can raise several questions. Here are some frequently asked questions and their detailed answers:
-
What is the square root of 325?
The square root of 325, denoted as \( \sqrt{325} \), is approximately 18.0278. This value is obtained using the square root function and can be verified through manual calculation or a calculator.
-
Is the square root of 325 a rational number?
No, the square root of 325 is not a rational number. Rational numbers are numbers that can be expressed as a fraction of two integers. Since 325 is not a perfect square, its square root is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal expansion is non-terminating and non-repeating.
-
How can you simplify \( \sqrt{325} \)?
The number 325 can be factored into prime numbers as \( 325 = 5^2 \times 13 \). Thus, the square root can be simplified using the prime factorization method:
\[
\sqrt{325} = \sqrt{5^2 \times 13} = 5 \times \sqrt{13} \approx 18.0278
\]This shows that \( \sqrt{325} \) simplifies to \( 5 \sqrt{13} \), which is a more manageable form for certain calculations.
-
What are some practical applications of the square root of 325?
Square roots are used in various fields such as physics, engineering, and statistics. For example, if you were designing a component that requires a diagonal of 325 units in geometry, knowing the square root helps in determining the dimensions. Similarly, in financial calculations, square roots can be used to calculate returns and volatility.
-
How do you compare the square root of 325 with nearby numbers?
To compare \( \sqrt{325} \) with the square roots of nearby numbers, you can observe the values in a square root table. For example, the square root of 324 is 18, and the square root of 326 is approximately 18.0555. These comparisons show that \( \sqrt{325} \) is slightly more than 18 and close to these nearby square roots.
-
Why is it important to understand square roots?
Understanding square roots is crucial for solving quadratic equations, analyzing geometric shapes, and performing various scientific and engineering calculations. They are also essential in understanding the concept of root-mean-square (RMS) values in statistics and signal processing, which measure the magnitude of varying quantities.
-
How do you calculate the square root of a number without a calculator?
To calculate the square root of a number manually, you can use methods such as:
- Prime Factorization: Factor the number into its prime factors and simplify if possible.
- Long Division Method: A step-by-step division-like process to find the square root to desired precision.
- Estimation and Refinement: Guess a number close to the square root and refine your guess using averaging or other methods.
For detailed steps, refer to the earlier section on manual calculation methods.
-
How can you use a calculator to find the square root of 325?Using a calculator to find \( \sqrt{325} \) is straightforward. Simply enter 325 and press the square root (√) button. This will give you the result of approximately 18.0278. For more detailed steps, refer to the section on using a calculator.
These questions cover the basics and some deeper insights into the square root of 325 and the concept of square roots in general.
Conclusion
The exploration of the square root of 325 provides a deeper understanding of the significance and applications of square roots in various contexts. By delving into the methods of calculation, comparison with nearby numbers, and practical uses, we gain a comprehensive view of how this mathematical concept integrates into both simple and complex problems.
Here are the key takeaways from our discussion:
- Approximation and Calculation: The square root of 325 is approximately 18.0278. This value can be computed using various methods, including manual calculations and digital tools like calculators. Understanding different techniques to find square roots enhances our ability to solve related problems effectively.
- Simplification: Simplifying square roots through prime factorization, such as representing \( \sqrt{325} \) as \( 5 \sqrt{13} \), helps in simplifying complex calculations and provides insight into the number’s properties.
- Comparative Analysis: Comparing the square roots of numbers around 325, like 320 and 330, highlights the smooth, continuous nature of the square root function. This comparative approach helps in approximating and understanding the behavior of square roots for different numbers.
- Applications: Square roots are not just abstract mathematical concepts; they have practical applications in geometry, physics, engineering, statistics, and financial mathematics. For instance, they are crucial in calculating distances, analyzing data, and understanding various scientific principles.
- Educational Importance: Learning about square roots enhances mathematical literacy and problem-solving skills. Whether through manual methods or using technology, the ability to work with square roots is fundamental to many areas of study and professional practice.
In summary, the square root of 325, like other square roots, is a fundamental mathematical concept with wide-ranging applications. By mastering its calculation and understanding its properties, we can better appreciate its role in both theoretical and practical scenarios.
We encourage further exploration and practice with square roots to solidify understanding and discover their utility in diverse fields.
Khám phá căn bậc hai của số 325 trong video này. Video hướng dẫn cách tính và ý nghĩa của căn bậc hai của 325.
Square Root of 325 - Căn bậc hai của 325
READ MORE:
Khám phá cách tính căn bậc hai của 325 một cách chi tiết và dễ hiểu. Video hữu ích cho học sinh và người yêu thích toán học.
Căn Bậc Hai Của 325