What is the Square Root of 35? Discover Its Value and Applications

The square root of 35 is an irrational number, which means it cannot be expressed as a simple fraction. However, it can be represented in various forms for practical use:

Decimal Form

The square root of 35 in decimal form is approximately:

\(\sqrt{35} \approx 5.916079783099616\)

Radical Form

In its simplest radical form, the square root of 35 remains:

Exponential Form

Using exponential notation, the square root of 35 can be written as:

\(35^{1/2}\)

Steps to Calculate the Square Root of 35

1. Estimate a number close to the square root. Since \(5^2 = 25\) and \(6^2 = 36\), \(\sqrt{35}\) is between 5 and 6.
2. Use a method like the Babylonian method (also known as Heron's method) to refine the estimate:
• Start with an initial guess, say 6.
• Average the guess with 35 divided by the guess: \(\frac{6 + \frac{35}{6}}{2}\).
• Repeat the process with the new estimate to improve accuracy.

Applications

The square root of 35 can be used in various mathematical and practical applications, such as:

• Geometry: Calculating distances and dimensions where 35 is part of an equation.
• Engineering: Solving problems involving quadratic equations and other calculations requiring square roots.
• Physics: Determining values in formulas where 35 is a given parameter.

Visual Representation

To visualize the square root of 35 on a number line, it would be slightly less than 6, placed between 5.9 and 6.

Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. For instance, the square root of 25 is 5 because \(5 \times 5 = 25\). Understanding square roots is essential for solving quadratic equations, performing geometric calculations, and analyzing scientific data.

Here's a step-by-step guide to understanding square roots:

1. Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). It is denoted as \(\sqrt{x}\).
2. Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For example, \(\sqrt{25} = 5\) and \(-\sqrt{25} = -5\).
3. Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are integers.
4. Irrational Numbers: Numbers that are not perfect squares have irrational square roots, meaning they cannot be expressed as exact fractions. For instance, \(\sqrt{35}\) is an irrational number.
5. Approximation Methods: To find the square root of a non-perfect square, methods like the Babylonian method (or Heron's method) can be used for approximation.

Understanding square roots helps in various fields, including:

• Geometry: Calculating distances, areas, and volumes.
• Engineering: Solving design and structural problems.
• Physics: Analyzing wave functions, velocities, and other physical phenomena.
• Everyday Use: Practical applications such as estimating dimensions and understanding scales.

The square root of 35 is a number that, when multiplied by itself, equals 35. This value is not an integer and is considered an irrational number, meaning it cannot be precisely expressed as a simple fraction. Let's delve into the details of the square root of 35:

Decimal Form:

The square root of 35 in decimal form is approximately:

\(\sqrt{35} \approx 5.916079783099616\)

Radical Form:

In its simplest radical form, the square root of 35 remains:

\(\sqrt{35}\)

Exponential Form:

Using exponential notation, the square root of 35 can be written as:

\(35^{1/2}\)

Calculation Methods:

To calculate the square root of 35, you can use the following methods:

1. Estimation: Since \(5^2 = 25\) and \(6^2 = 36\), the square root of 35 is between 5 and 6.
2. Babylonian Method:
   1. Start with an initial guess (e.g., 6).
   2. Average the guess with 35 divided by the guess: \(\frac{6 + \frac{35}{6}}{2} \approx 5.916\).
   3. Repeat the process with the new estimate to improve accuracy.
3. Calculator: Use a scientific calculator to find a more precise value.

Applications:

The square root of 35 can be used in various fields, such as:

• Geometry: Determining the length of the diagonal of a rectangle or other geometric shapes where 35 is involved.
• Engineering: Solving problems involving quadratic equations and other calculations requiring square roots.
• Physics: Calculating values in formulas where 35 is a given parameter, such as certain energy levels or distances.

Understanding and calculating the square root of 35 is essential for various mathematical and practical applications, helping to solve real-world problems effectively.

The square root of 35 can be expressed in both decimal and radical forms, each useful in different contexts. Let's explore these forms in detail:

Decimal Form:

The decimal form of the square root of 35 is an approximation, as it is an irrational number. It cannot be precisely expressed as a finite decimal or fraction. The value is approximately:

\(\sqrt{35} \approx 5.916079783099616\)

This approximation is useful for practical calculations and when a numerical answer is required. It can be further rounded to the desired number of decimal places, such as 5.92 or 5.916.

Radical Form:

The radical form is the exact representation of the square root of 35 and is written as:

\(\sqrt{35}\)

This form is often used in algebra and higher-level mathematics because it maintains the exact value without approximation. It is particularly useful when performing symbolic manipulation or when an exact answer is needed.

Comparing Decimal and Radical Forms:

Each form has its own advantages and applications:

• Decimal Form:
  • Useful for practical calculations and numerical problem-solving.
  • Provides a quick and understandable approximation.
  • Preferred in scientific and engineering contexts where measurements and precision are important.
• Radical Form:
  • Maintains the exact value without loss of precision.
  • Useful in algebraic manipulation and solving equations.
  • Preferred in pure mathematics for exact representations.

Understanding both the decimal and radical forms of the square root of 35 is essential for different mathematical tasks. While the decimal form provides a practical approximation, the radical form offers an exact representation that is invaluable in various mathematical analyses.

Calculating the square root of 35 involves several methods, ranging from basic estimation to more precise techniques. Here, we explore different methods to find \(\sqrt{35}\) step by step:

1. Estimation:

Estimating the square root is a quick way to find an approximate value.

1. Identify the perfect squares closest to 35. Since \(5^2 = 25\) and \(6^2 = 36\), \(\sqrt{35}\) lies between 5 and 6.
2. Refine the estimate by noting that 35 is closer to 36 than to 25, suggesting \(\sqrt{35}\) is slightly less than 6.
3. Using further refinement, \(\sqrt{35}\) is approximately 5.9.

2. Babylonian (Heron's) Method:

This iterative method provides a more precise value:

1. Start with an initial guess, \(x_0\). Let's use 6.
2. Apply the formula: \(x_{n+1} = \frac{1}{2} \left(x_n + \frac{35}{x_n}\right)\).
3. Iterate until the value stabilizes:
   • First iteration: \(x_1 = \frac{1}{2} \left(6 + \frac{35}{6}\right) \approx 5.9167\).
   • Second iteration: \(x_2 = \frac{1}{2} \left(5.9167 + \frac{35}{5.9167}\right) \approx 5.9161\).
   • Continue iterating to achieve desired precision.

3. Using a Calculator:

A scientific calculator can quickly provide a precise value for \(\sqrt{35}\). Simply enter 35 and press the square root function to get approximately 5.916079783099616.

4. Long Division Method:

The long division method is a manual algorithm for finding square roots:

1. Group the digits of 35 into pairs: 35.
2. Find the largest integer whose square is less than or equal to 35. This is 5 (since \(5^2 = 25\)).
3. Subtract 25 from 35 to get 10. Bring down pairs of zeros to continue the division.
4. Double the divisor (5) to get 10. Determine the next digit by finding the largest digit \(d\) such that \(10d \times d \leq 1000\).
5. Repeat the process to achieve desired precision.

5. Newton's Method:

Newton's method, like the Babylonian method, uses iterative approximation:

1. Start with an initial guess \(x_0\). For instance, 6.
2. Apply the formula: \(x_{n+1} = \frac{x_n + \frac{35}{x_n}}{2}\).
3. Iterate until convergence:
   • First iteration: \(x_1 = \frac{6 + \frac{35}{6}}{2} \approx 5.9167\).
   • Second iteration: \(x_2 = \frac{5.9167 + \frac{35}{5.9167}}{2} \approx 5.9161\).
   • Continue iterating for more precision.

Each method has its applications, with estimation providing quick answers and iterative methods offering precise values. Understanding these methods enhances your mathematical toolkit for solving square root problems.

Approximating the square root of 35 involves using various techniques to get as close as possible to the true value. Here are some commonly used methods for approximation:

1. Estimation by Comparing Perfect Squares:

1. Identify the perfect squares closest to 35: 25 (\(5^2\)) and 36 (\(6^2\)).
2. Since 35 is closer to 36, \(\sqrt{35}\) is slightly less than 6.
3. Refining further, estimate \(\sqrt{35} \approx 5.9\).

2. Babylonian (Heron's) Method:

This iterative method provides a more precise approximation.

1. Start with an initial guess, \(x_0\). Let's use 6.
2. Apply the formula: \(x_{n+1} = \frac{1}{2} \left(x_n + \frac{35}{x_n}\right)\).
3. Iterate until the value stabilizes:
   • First iteration: \(x_1 = \frac{1}{2} \left(6 + \frac{35}{6}\right) \approx 5.9167\).
   • Second iteration: \(x_2 = \frac{1}{2} \left(5.9167 + \frac{35}{5.9167}\right) \approx 5.9161\).
   • Continue iterating to achieve the desired precision.

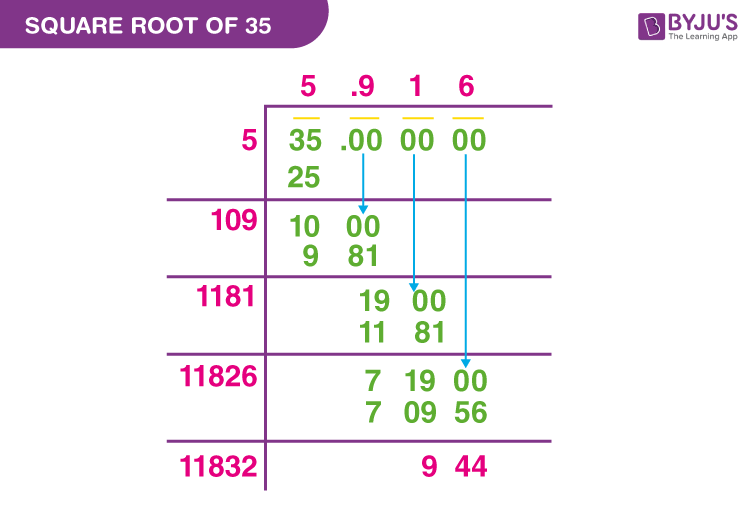
3. Long Division Method:

This manual algorithm helps find square roots to a high degree of precision.

1. Group the digits of 35 into pairs: 35.
2. Find the largest integer whose square is less than or equal to 35. This is 5 (since \(5^2 = 25\)).
3. Subtract 25 from 35 to get 10. Bring down pairs of zeros to continue the division.
4. Double the divisor (5) to get 10. Determine the next digit by finding the largest digit \(d\) such that \(10d \times d \leq 1000\).
5. Repeat the process to achieve the desired precision.

4. Newton's Method:

Similar to the Babylonian method, this iterative method refines the estimate:

1. Start with an initial guess \(x_0\), such as 6.
2. Apply the formula: \(x_{n+1} = \frac{x_n + \frac{35}{x_n}}{2}\).
3. Iterate until convergence:
   • First iteration: \(x_1 = \frac{6 + \frac{35}{6}}{2} \approx 5.9167\).
   • Second iteration: \(x_2 = \frac{5.9167 + \frac{35}{5.9167}}{2} \approx 5.9161\).
   • Continue iterating for more precision.

5. Calculator Use:

Using a scientific calculator provides a quick and precise approximation:

• Enter 35 and press the square root function to get \(\sqrt{35} \approx 5.916079783099616\).

These approximation techniques provide various ways to estimate the square root of 35, from quick estimations to highly precise calculations. Understanding and applying these methods can enhance problem-solving skills in mathematics and related fields.

The square root of 35, approximately 5.916, finds its utility in various practical and theoretical applications across different fields. Here are some significant applications:

• Geometry

  In geometry, the square root of 35 is used to determine the length of the diagonal of rectangles and the side lengths of squares when their area is known. For example, if a square has an area of 35 square units, its side length is √35 units.

  Additionally, it can be used in problems involving the Pythagorean theorem to find the lengths of sides in right-angled triangles.

• Engineering

  Engineering applications often involve the square root of 35 in calculations related to structural design and analysis. For instance, engineers might use it to determine material strengths, load distributions, and dimensions in various construction projects.

  In electrical engineering, √35 may appear in formulas related to signal processing and circuit design where root calculations are required.

• Physics

  In physics, the square root of 35 can be used in kinematic equations and to solve problems related to motion and forces. For instance, calculating the time it takes for an object to fall from a certain height or the speed of an object given the distance covered.

  It also appears in wave equations and other scenarios involving natural frequencies and oscillations.

• Everyday Applications

  Square roots are common in daily life, such as determining the dimensions of square objects like garden plots, tiles, or rooms when given the area. Knowing the square root helps in optimizing space and material usage effectively.

Overall, the square root of 35 is a versatile mathematical constant with widespread applications in various disciplines, aiding in precise calculations and problem-solving.

The square root of 35, approximately \( \sqrt{35} \approx 5.916 \), finds various applications in geometry, particularly in calculating distances, areas, and constructing geometric shapes. Here are some notable applications:

• Diagonal of a Rectangle:

  In a rectangle where one side is 5 units and the other side is approximately 7 units, the diagonal can be calculated using the Pythagorean theorem:

  \[
  d = \sqrt{5^2 + 7^2} = \sqrt{25 + 49} = \sqrt{74}
  \]
  Approximating, this results in \( d \approx 8.6 \) units, which is close to the context where \( \sqrt{35} \) might appear as a sub-component in more complex shapes.

• Distance Between Points:

  Consider two points in a coordinate system, \( A = (3, 2) \) and \( B = (-2, 5) \). The distance \( AB \) between these points is given by:

  \[
  AB = \sqrt{(3 - (-2))^2 + (2 - 5)^2} = \sqrt{(3 + 2)^2 + (-3)^2} = \sqrt{5^2 + 3^2} = \sqrt{25 + 9} = \sqrt{34}
  \]
  While this does not directly equal \( \sqrt{35} \), the calculation methods and the appearance of such irrational roots are common in coordinate geometry.

• Triangles and Trigonometry:

  In a right triangle, if one leg is 5 units and the hypotenuse is slightly greater than 6 units, the length of the other leg can be derived using the square root of 35:

  \[
  c = \sqrt{a^2 + b^2} \implies b = \sqrt{c^2 - a^2} = \sqrt{36 - 25} = \sqrt{11} \approx 3.317
  \]
  Here, \( \sqrt{35} \) may emerge in trigonometric calculations involving similar triangles.

• Area of Triangles:

  In an isosceles triangle where the equal sides are 6 units and the base is derived from the root, the height can be found using the formula for the area:

  \[
  h = \sqrt{a^2 - \left(\frac{b}{2}\right)^2} = \sqrt{6^2 - \left(\frac{\sqrt{35}}{2}\right)^2} = \sqrt{36 - 8.75} \approx 5.096
  \]
  This highlights the application of \( \sqrt{35} \) in determining dimensions and solving for unknowns in geometric contexts.

The square root of 35 (\(\sqrt{35} \approx 5.916\)) has various applications in the field of engineering. These applications span across different branches such as structural, electrical, and mechanical engineering. Understanding and utilizing \(\sqrt{35}\) can help engineers in several critical calculations and design processes.

Structural Engineering

In structural engineering, the natural frequency of structures like bridges and buildings is often determined using square roots. The natural frequency helps in predicting how a structure will react to different loads, such as wind or traffic. The formula for natural frequency (f) involves the square root of stiffness (k) divided by mass (m):

\[
f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\]

Using \(\sqrt{35}\), engineers can refine their calculations to ensure the stability and safety of structures under various load conditions.

Electrical Engineering

In electrical engineering, square roots are used to compute power, voltage, and current in circuits. For instance, the Root Mean Square (RMS) value of alternating current (AC) voltage is calculated using square roots to find the effective voltage. The RMS value (V_RMS) is given by:

\[
V_{RMS} = V_{peak} \times \frac{\sqrt{2}}{2}
\]

When dealing with non-standard voltages, such as 35V peak, the square root calculation becomes essential.

Mechanical Engineering

In mechanical engineering, the square root of 35 can be used in vibration analysis of machinery. The frequency of vibrations (\(\omega\)) can be found using the square root of the stiffness (k) over mass (m) formula:

\[
\omega = \sqrt{\frac{k}{m}}
\]

Accurate vibration analysis helps in designing more efficient and durable mechanical systems.

Fluid Mechanics

In fluid mechanics, the Darcy-Weisbach equation is used to calculate pressure loss due to friction in pipes. The equation involves the square root of the Reynolds number (Re) and other parameters:

\[
\Delta P = f \left( \frac{L}{D} \right) \left( \frac{\rho V^2}{2} \right)
\]

Where \(f\) is the friction factor, \(L\) is the pipe length, \(D\) is the diameter, \(\rho\) is the density, and \(V\) is the velocity. In cases where parameters align to \(\sqrt{35}\), precise calculations are critical for system efficiency.

Acoustical Engineering

In acoustical engineering, sound intensity levels involve logarithmic scales where square roots are frequently used. The intensity (I) is related to the pressure (P) by the formula:

\[
I = \frac{P^2}{\rho c}
\]

where \(\rho\) is the density of the medium and \(c\) is the speed of sound. Accurate pressure measurements often necessitate the use of square roots in the analysis.

Overall, the square root of 35 is an essential mathematical tool in engineering, aiding in the precise calculation and analysis required for designing and maintaining various engineering systems and structures.

The square root of 35, approximately 5.916, finds several applications in physics, particularly in areas requiring precise measurements and calculations. Here are some notable examples:

• Kinematics: In physics, the square root of non-perfect squares, like 35, is often encountered in equations involving motion. For instance, if an object is in free fall, the distance covered (s) in time (t) can be expressed as \( s = \frac{1}{2} g t^2 \). Solving for time when the distance is 35 meters involves taking the square root of 35.
• Wave Mechanics: The frequency (f) and wavelength (λ) of a wave are related by the equation \( v = f \lambda \), where v is the wave speed. When calculating the frequency of a wave with a wavelength that results in an expression involving the square root of 35, such calculations become necessary.
• Electromagnetism: In problems involving electromagnetic waves, especially when dealing with resonance frequencies or the impedance of circuits, the square root of 35 may appear in the mathematical derivations of wave equations or resonance conditions.
• Quantum Mechanics: The square root of non-perfect squares like 35 can appear in quantum mechanics, particularly in wave function normalization and in the calculation of probability amplitudes where precise values are crucial.

Here is an example calculation involving the square root of 35 in a physics context:

Thus, the square root of 35 is instrumental in solving various physics problems, highlighting its importance in scientific calculations and practical applications.

Understanding the square root of 35 can be greatly enhanced through visual representations. Here are a few methods to visualize this irrational number:

Number Line Representation

One way to visualize the square root of 35 is by placing it on a number line:

• Draw a number line with evenly spaced intervals.
• Mark the integers 5 and 6, since \(5^2 = 25\) and \(6^2 = 36\). The square root of 35 lies between these two numbers.
• Place a point approximately at 5.916 to represent \(\sqrt{35}\).

Geometric Representation

Another method involves using geometric shapes:

• Draw a right triangle where one leg is 5 units and the hypotenuse is \(\sqrt{35}\) units.
• Using the Pythagorean theorem: \(c^2 = a^2 + b^2\), we set \(c = \sqrt{35}\), \(a = 5\), and solve for \(b\).
• This shows that \(\sqrt{35}\) is the hypotenuse of a triangle with specific leg lengths, providing a visual understanding.

Graphical Representation

Graphing the function \(y = \sqrt{x}\) can also help visualize the square root of 35:

• Plot the curve of \(y = \sqrt{x}\) on a graph.
• Find the point where \(x = 35\) and read the corresponding \(y\)-value.
• This point \((35, \sqrt{35})\) shows how \(\sqrt{35}\) relates to other square roots on the graph.

Using Technology

Modern technology provides tools for visualizing square roots:

• Graphing calculators can plot \(y = \sqrt{x}\) and directly show the point for \(x = 35\).
• Software like GeoGebra or Desmos allows for interactive exploration of the square root function.

These visual tools help in understanding the position and magnitude of \(\sqrt{35}\) in a more intuitive manner.

Technology has significantly simplified the process of finding square roots, including the square root of 35. Below are several methods to calculate the square root of 35 using various technological tools:

• Calculators:

  Most modern calculators come with a square root function. To find the square root of 35, simply enter 35 and press the square root (√) button. This will yield an approximate value of:

  \[
  \sqrt{35} \approx 5.916
  \]

• Spreadsheet Software:

  Programs like Microsoft Excel, Google Sheets, and Apple Numbers can also be used to find the square root. In these programs, you can use the =SQRT() function. For example, entering =SQRT(35) in a cell will display the square root of 35, approximately:

  \[
  \sqrt{35} \approx 5.9160797831
  \]

• Online Calculators:

  Various websites offer online calculators that can compute the square root of 35. Simply input 35 into the designated field and select the square root function. These tools are convenient and readily available.

• Programming Languages:

  Several programming languages have built-in functions to calculate square roots. For example:

  • In Python, you can use math.sqrt(35):

  \[
  \text{import math} \newline
  \text{math.sqrt(35)} \approx 5.9160797831
  \]

  • In JavaScript, use Math.sqrt(35):

  \[
  \text{Math.sqrt(35)} \approx 5.9160797831
  \]

These technological methods not only provide quick and accurate results but also make it easy to perform additional calculations and analyze data involving the square root of 35.

There are several common misconceptions about square roots, which can lead to misunderstandings and errors in calculations. Here, we address some of the most prevalent misconceptions related to the square root of 35:

• Square Roots Always Have Two Values:

  One common misconception is that the square root of a number always has two values, often stated as \( \pm \sqrt{n} \). While it is true that the equation \( x^2 = n \) has two solutions, \( x = \pm \sqrt{n} \), the square root function itself, \( \sqrt{n} \), is defined to return only the principal (non-negative) value. Therefore, \( \sqrt{35} \approx 5.92 \) is a single positive value, not \( \pm 5.92 \).

• Misunderstanding the Pythagorean Theorem:

  Another misconception arises in the context of the Pythagorean theorem. Some believe that if \( a^2 + b^2 = c^2 \), then \( a, b, \) and \( c \) must be the side lengths of a right triangle. However, this relationship only holds true if \( c \) is the longest side (hypotenuse). Mixing up the sides or applying this incorrectly to non-right triangles leads to errors.

• Confusion Between Square Roots and Squares:

  It is often mistakenly believed that the operations of squaring and taking the square root are direct inverses for all numbers. For example, some may think that \( \sqrt{x^2} = x \) for any real number \( x \). However, \( \sqrt{x^2} \) actually equals \( |x| \), the absolute value of \( x \), to ensure the result is non-negative.

• Incorrect Use of Square Root in Geometry:

  In geometry, students might incorrectly apply square roots when dealing with areas and side lengths. For example, misunderstanding that the square root of an area does not directly translate to a side length unless the shape is a perfect square. For instance, if the area of a rectangle is 35 square units, its side lengths are not simply \( \sqrt{35} \), but depend on the specific dimensions of the rectangle.

• Believing Non-Integer Square Roots are Always Irrational:

  While many non-integer square roots are irrational, this is not always the case. It is a misconception to believe that all non-integer square roots must be irrational. However, in the case of 35, \( \sqrt{35} \) is indeed an irrational number as it cannot be expressed as a simple fraction.

• What is the square root of 35?

  The square root of 35 is approximately 5.9160797831.

• Is the square root of 35 a rational number?

  No, the square root of 35 is an irrational number because it cannot be expressed as a fraction of two integers. Its decimal representation is non-repeating and non-terminating.

• How can I calculate the square root of 35 manually?

  You can use methods like the long division method or approximation techniques to calculate the square root manually. However, using a calculator is the easiest way to find an accurate result.

• What are some applications of the square root of 35?

  The square root of 35 can be used in various fields such as geometry for calculating distances and areas, in engineering for designing components, and in physics for solving equations involving square roots.

• Why is it important to understand the square root of non-perfect squares like 35?

  Understanding the square roots of non-perfect squares is crucial in higher-level mathematics and science as it helps in solving real-world problems where precise measurements and calculations are required.

• Can the square root of 35 be simplified further?

  No, the square root of 35 cannot be simplified further because 35 is not a product of a perfect square and another integer.

The square root of 35, approximately 5.916, is a valuable concept in various mathematical and practical applications. Throughout this guide, we have explored different methods to calculate it, its representation in radical and decimal forms, and its relevance across different fields such as geometry, engineering, and physics.

Understanding the square root of 35 helps in solving complex problems and enhancing analytical skills. By employing techniques like the long division method, technological tools, and visualization strategies, one can accurately determine the square root and apply this knowledge effectively.

From geometrical constructions to engineering computations and physical phenomena, the square root of 35 plays a crucial role. Additionally, clarifying common misconceptions ensures a solid foundational understanding. This comprehensive guide aims to equip learners and practitioners with the necessary tools and insights to utilize the square root of 35 confidently in various contexts.

In conclusion, mastering the concept of square roots, particularly that of 35, opens doors to deeper mathematical comprehension and practical application, fostering a greater appreciation for the beauty and utility of mathematics in our everyday lives.