Topic square root of 3200: Discover the easy steps to calculate the square root of 3200. This guide will help you understand the concept, perform the calculation accurately, and explore its practical applications. Whether you're a student or just curious, you'll find this information both informative and engaging. Let's dive into the fascinating world of square roots!
Table of Content
- Calculation of the Square Root of 3200
- Introduction to Square Roots
- Understanding the Concept of Square Root
- Basic Properties of Square Roots
- Methods to Calculate Square Roots
- Prime Factorization Method
- Long Division Method
- Approximating Square Roots
- Calculating the Square Root of 3200
- Step-by-Step Guide to Finding the Square Root of 3200
- Prime Factorization of 3200
- Exact Form of the Square Root of 3200
- Decimal Approximation of the Square Root of 3200
- Applications of Square Roots in Real Life
- Common Mistakes and Misconceptions
- Advanced Topics in Square Roots
- Square Roots in Higher Mathematics
- Practice Problems and Solutions
- Frequently Asked Questions (FAQs)
- YOUTUBE: Khám phá cách tính căn bậc hai của 3200 một cách chi tiết và dễ hiểu. Học các phương pháp khác nhau và ứng dụng thực tế của căn bậc hai.
Calculation of the Square Root of 3200
The square root of a number is a value that, when multiplied by itself, gives the original number. To find the square root of 3200, we can use the following steps:
Prime Factorization
First, we perform the prime factorization of 3200:
- 3200 is divisible by 2: \(3200 \div 2 = 1600\)
- 1600 is divisible by 2: \(1600 \div 2 = 800\)
- 800 is divisible by 2: \(800 \div 2 = 400\)
- 400 is divisible by 2: \(400 \div 2 = 200\)
- 200 is divisible by 2: \(200 \div 2 = 100\)
- 100 is divisible by 2: \(100 \div 2 = 50\)
- 50 is divisible by 2: \(50 \div 2 = 25\)
- 25 is divisible by 5: \(25 \div 5 = 5\)
- 5 is divisible by 5: \(5 \div 5 = 1\)
So, the prime factorization of 3200 is: \(3200 = 2^7 \times 5^2\)
Calculating the Square Root
The square root of a product is the product of the square roots of the factors. Thus:
\[
\sqrt{3200} = \sqrt{2^7 \times 5^2} = \sqrt{2^7} \times \sqrt{5^2}
\]
Since \(\sqrt{2^7} = 2^{3.5}\) and \(\sqrt{5^2} = 5\), we get:
\[
\sqrt{3200} = 2^{3.5} \times 5 = (2^3 \times 2^{0.5}) \times 5 = 8 \times \sqrt{2} \times 5 = 40\sqrt{2}
\]
Decimal Approximation
For a decimal approximation, we know that \(\sqrt{2} \approx 1.414\). Therefore:
\[
40\sqrt{2} \approx 40 \times 1.414 = 56.56
\]
Summary
The exact value of \(\sqrt{3200}\) is \(40\sqrt{2}\), and the decimal approximation is approximately 56.56.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is a fundamental concept in mathematics with various applications in science, engineering, and everyday life.
The square root symbol is \( \sqrt{} \), and the square root of a number \( x \) is written as \( \sqrt{x} \). For example, the square root of 16 is written as \( \sqrt{16} = 4 \), because \( 4 \times 4 = 16 \).
To understand square roots better, let's look at some key points:
- The square root of a positive number is always positive. For instance, \( \sqrt{25} = 5 \).
- Every positive number has two square roots: a positive root and a negative root. For example, the square roots of 25 are \( \pm5 \) because \( 5 \times 5 = 25 \) and \( -5 \times -5 = 25 \).
- The square root of 0 is 0: \( \sqrt{0} = 0 \).
- Square roots of negative numbers are not real numbers; they are complex numbers. For example, \( \sqrt{-1} \) is an imaginary unit \( i \), where \( i^2 = -1 \).
Let's consider the example of finding the square root of 3200:
- Prime Factorization: Break down 3200 into its prime factors:
- 3200 ÷ 2 = 1600
- 1600 ÷ 2 = 800
- 800 ÷ 2 = 400
- 400 ÷ 2 = 200
- 200 ÷ 2 = 100
- 100 ÷ 2 = 50
- 50 ÷ 2 = 25
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
This gives us: \( 3200 = 2^7 \times 5^2 \).
- Calculate the Square Root: Use the property of square roots that \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \):
\( \sqrt{3200} = \sqrt{2^7 \times 5^2} = \sqrt{2^7} \times \sqrt{5^2} = 2^{3.5} \times 5 \).
Simplify to get \( 2^{3.5} = 2^3 \times 2^{0.5} = 8 \times \sqrt{2} \), so \( \sqrt{3200} = 40 \sqrt{2} \).
Thus, the exact form of the square root of 3200 is \( 40 \sqrt{2} \), and its decimal approximation is approximately 56.57.
Understanding the Concept of Square Root
The square root of a number is a value that, when multiplied by itself, equals the original number. This concept is fundamental in mathematics and appears frequently in algebra, geometry, and various real-world applications.
To illustrate the concept, let's consider the square root of 25. Since \( 5 \times 5 = 25 \), we say that the square root of 25 is 5, written as \( \sqrt{25} = 5 \).
Here are some important properties and facts about square roots:
- Non-Negative Roots: The square root of a non-negative number is non-negative. For instance, \( \sqrt{36} = 6 \).
- Two Possible Roots: Every positive number has two square roots: a positive and a negative root. For example, the square roots of 36 are \( \pm 6 \) because both \( 6 \times 6 = 36 \) and \( (-6) \times (-6) = 36 \).
- Square Root of Zero: The square root of zero is zero: \( \sqrt{0} = 0 \).
- Complex Roots: Negative numbers do not have real square roots; their roots are complex numbers. For example, \( \sqrt{-9} = 3i \), where \( i \) is the imaginary unit with the property \( i^2 = -1 \).
Let's delve deeper into the concept with a step-by-step example of finding the square root of 3200:
- Prime Factorization: Break down 3200 into its prime factors:
- 3200 ÷ 2 = 1600
- 1600 ÷ 2 = 800
- 800 ÷ 2 = 400
- 400 ÷ 2 = 200
- 200 ÷ 2 = 100
- 100 ÷ 2 = 50
- 50 ÷ 2 = 25
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
Thus, the prime factorization of 3200 is \( 3200 = 2^7 \times 5^2 \).
- Calculating the Square Root: Apply the property of square roots that \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \):
\( \sqrt{3200} = \sqrt{2^7 \times 5^2} = \sqrt{2^7} \times \sqrt{5^2} = 2^{3.5} \times 5 \).
Simplify \( 2^{3.5} = 2^3 \times 2^{0.5} = 8 \times \sqrt{2} \), hence \( \sqrt{3200} = 40 \sqrt{2} \).
The exact form of the square root of 3200 is \( 40 \sqrt{2} \), and its decimal approximation is around 56.57. Understanding these steps helps in grasping the broader concept of square roots and their applications.
Basic Properties of Square Roots
Understanding the basic properties of square roots is crucial for solving various mathematical problems. Here are the fundamental properties:
- Non-Negative Output: The square root of a non-negative number is always non-negative. For example, \( \sqrt{25} = 5 \).
- Two Roots for Positive Numbers: Every positive number has two square roots: a positive root and a negative root. For instance, the square roots of 25 are \( \pm 5 \) because \( 5 \times 5 = 25 \) and \( -5 \times -5 = 25 \).
- Zero Property: The square root of zero is zero: \( \sqrt{0} = 0 \).
- Product Property: The square root of a product is the product of the square roots of the factors. For example, \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \). For instance, \( \sqrt{36} = \sqrt{4 \times 9} = \sqrt{4} \times \sqrt{9} = 2 \times 3 = 6 \).
- Quotient Property: The square root of a quotient is the quotient of the square roots of the numerator and denominator. For example, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), provided \( b \neq 0 \).
- Power of 2: The square root of a number squared is the absolute value of the original number: \( \sqrt{x^2} = |x| \). For instance, \( \sqrt{(-5)^2} = \sqrt{25} = 5 \).
- Square Roots of Negative Numbers: Negative numbers do not have real square roots; their square roots are complex numbers. For example, \( \sqrt{-1} = i \), where \( i \) is the imaginary unit with the property \( i^2 = -1 \).
Let's apply these properties to find the square root of 3200:
- Prime Factorization: First, break down 3200 into its prime factors:
- 3200 ÷ 2 = 1600
- 1600 ÷ 2 = 800
- 800 ÷ 2 = 400
- 400 ÷ 2 = 200
- 200 ÷ 2 = 100
- 100 ÷ 2 = 50
- 50 ÷ 2 = 25
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
So, the prime factorization of 3200 is \( 3200 = 2^7 \times 5^2 \).
- Applying the Product Property: Using the product property of square roots:
\( \sqrt{3200} = \sqrt{2^7 \times 5^2} = \sqrt{2^7} \times \sqrt{5^2} \).
Simplify the expression:
\( \sqrt{2^7} = 2^{7/2} = 2^{3.5} = 2^3 \times 2^{0.5} = 8 \times \sqrt{2} \).
\( \sqrt{5^2} = 5 \).
Thus, \( \sqrt{3200} = 8 \times \sqrt{2} \times 5 = 40 \sqrt{2} \).
Therefore, the exact form of the square root of 3200 is \( 40 \sqrt{2} \), and its decimal approximation is approximately 56.57. Understanding these properties helps simplify and solve square root problems efficiently.
Methods to Calculate Square Roots
Calculating square roots can be done using various methods, each suited for different purposes and levels of precision. Here are some common methods:
1. Prime Factorization Method
This method involves breaking down the number into its prime factors and then applying the square root to each factor. Let's apply this to find the square root of 3200:
- Prime Factorization: Decompose 3200 into its prime factors:
- 3200 ÷ 2 = 1600
- 1600 ÷ 2 = 800
- 800 ÷ 2 = 400
- 400 ÷ 2 = 200
- 200 ÷ 2 = 100
- 100 ÷ 2 = 50
- 50 ÷ 2 = 25
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
So, the prime factorization of 3200 is \( 3200 = 2^7 \times 5^2 \).
- Applying the Square Root: Use the property of square roots:
\( \sqrt{3200} = \sqrt{2^7 \times 5^2} = \sqrt{2^7} \times \sqrt{5^2} \).
Simplify each square root:
\( \sqrt{2^7} = 2^{3.5} = 2^3 \times 2^{0.5} = 8 \times \sqrt{2} \).
\( \sqrt{5^2} = 5 \).
Thus, \( \sqrt{3200} = 8 \times \sqrt{2} \times 5 = 40 \sqrt{2} \).
The exact value is \( 40 \sqrt{2} \), and the approximate value is 56.57.
2. Long Division Method
This method is useful for finding the square roots of numbers that are not perfect squares. It involves a step-by-step division process:
- Start by grouping the digits of the number in pairs from right to left. For 3200, it becomes (32)(00).
- Find the largest number whose square is less than or equal to the first group. In this case, 5, because \( 5^2 = 25 \).
- Subtract the square from the first group and bring down the next pair of digits. Repeat the process for the remainder. Continue until all pairs are processed.
- The quotient obtained in this process is the square root.
This method provides a decimal approximation of the square root, which is useful when an exact form is not required.
3. Estimation and Approximation Method
This method is useful for quickly estimating the square root:
- Identify two perfect squares between which the number lies. For 3200, it lies between \( \sqrt{2500} = 50 \) and \( \sqrt{3600} = 60 \).
- Estimate the value closer to the actual square root by checking midpoints. For example, since 3200 is closer to 3600, the square root is closer to 60.
- Refine the estimate by averaging if necessary. Using this method, you can quickly estimate that \( \sqrt{3200} \approx 56.57 \).
4. Using a Calculator
For a quick and accurate result, you can use a scientific calculator:
- Enter the number 3200 into the calculator.
- Press the square root (√) function.
- The calculator will display the result, which is approximately 56.57.
5. Newton's Method (Iterative Method)
This method uses an iterative approach to find an approximation of the square root:
- Choose an initial guess \( x_0 \). For 3200, a reasonable guess might be 50.
- Apply the iteration formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{3200}{x_n} \right) \).
- Repeat the iteration until the value converges to a stable number. This iterative process improves the approximation with each step.
Newton's method is very efficient and converges quickly to a precise value.

Prime Factorization Method
The prime factorization method is a systematic approach to finding the square root of a number by breaking it down into its prime factors. This method is especially useful for simplifying the square root of large numbers. Here’s a step-by-step guide to using the prime factorization method to find the square root of 3200:
- Find the Prime Factors:
First, divide the number by the smallest prime number (2) and continue dividing by prime numbers until you reach 1. Write down each divisor:
- 3200 ÷ 2 = 1600
- 1600 ÷ 2 = 800
- 800 ÷ 2 = 400
- 400 ÷ 2 = 200
- 200 ÷ 2 = 100
- 100 ÷ 2 = 50
- 50 ÷ 2 = 25
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
So, the prime factorization of 3200 is:
\( 3200 = 2^7 \times 5^2 \)
- Group the Factors:
Group the prime factors into pairs of the same number. Each pair of prime factors will come out of the square root as a single factor:
- There are seven 2's, which can be grouped into three pairs of 2's (with one 2 left over).
- There are two 5's, which form one pair of 5's.
- Apply the Square Root:
Take the square root of each pair and multiply the results together. For any unpaired factors, leave them inside the square root:
\( \sqrt{3200} = \sqrt{2^7 \times 5^2} = \sqrt{2^6 \times 2 \times 5^2} = \sqrt{(2^3)^2 \times 2 \times 5^2} = 2^3 \times 5 \times \sqrt{2} \)
Simplify the expression:
\( 2^3 = 8 \)
\( 5 = 5 \)
So, the square root of 3200 is:
\( \sqrt{3200} = 8 \times 5 \times \sqrt{2} = 40 \sqrt{2} \)
The exact value of the square root of 3200 is \( 40 \sqrt{2} \), and its approximate decimal value is 56.57. Using the prime factorization method not only helps in finding the square root but also in understanding the structure and properties of numbers.
Long Division Method
The long division method is a systematic and manual way of calculating the square root of a number. It is particularly useful for finding the square root of numbers that are not perfect squares. Here’s a step-by-step guide to using the long division method to find the square root of 3200:
- Setup:
Write the number (3200) under the long division symbol. Pair the digits from right to left. For 3200, the pairs are (32)(00).
- Find the Largest Square:
Find the largest number whose square is less than or equal to the first pair (32). This number is 5, since \( 5^2 = 25 \) and \( 6^2 = 36 \), which is too large.
- Subtract and Bring Down:
Subtract the square of 5 (25) from the first pair (32) to get 7. Bring down the next pair of digits (00) to get 700.
Write 5 above the division line.
- Double the Quotient:
Double the current quotient (5) to get 10. Write this as the new divisor with a blank digit to the right (10_).
- Find the Next Digit:
Find the largest digit (x) such that \( 10x \times x \leq 700 \). This digit is 6 because \( 106 \times 6 = 636 \) and \( 107 \times 7 = 749 \), which is too large.
Write 6 next to 5 in the quotient.
- Repeat the Process:
Subtract 636 from 700 to get 64. Bring down two zeros to get 6400. Double the current quotient (56) to get 112, and write it with a blank digit to the right (112_).
Find the next digit (x) such that \( 112x \times x \leq 6400 \). This digit is 5 because \( 1125 \times 5 = 5625 \) and \( 1126 \times 6 = 6756 \), which is too large.
Write 5 next to 56 in the quotient.
- Continue for More Precision:
If more decimal places are needed, continue the process by bringing down pairs of zeros and repeating the steps.
Using this method, the quotient we get is 56.5, which is a close approximation of the square root of 3200. To increase accuracy, the process can be continued to more decimal places.
The long division method is a reliable technique for finding the square root, offering a good balance between manual calculation and understanding of the number's properties.
Approximating Square Roots
Approximating the square root of a number can be useful when an exact value is not necessary or when a quick estimation is needed. There are several methods to approximate square roots, including using average estimates and linear interpolation. Here, we will discuss a simple and effective method for approximating the square root of a number: the method of successive averaging.
Method of Successive Averaging
This method involves making an initial guess and then refining that guess through a series of averages. Let's apply this method to approximate the square root of 3200.
- Initial Guess: Choose a number that is close to the square root of 3200. We know that the square root of 3200 is between 50 and 60 because \(50^2 = 2500\) and \(60^2 = 3600\). Let's start with an initial guess of 55.
- Calculate the Average: Divide 3200 by your initial guess and then find the average of the result and the initial guess.
\( x = 58.18 \)Now, average this result with the initial guess:
\( x = 56.59 \) - Refine the Guess: Use this new average as your next guess and repeat the process.
\( x = 56.56 \)Average this result with your previous guess:
\( x = 56.575 \) - Continue Refining: Continue this process until the change between successive averages is minimal. This indicates that you have reached a good approximation. For example, another iteration might give:
\( x = 56.57 \)Average this result with your previous guess:
\( x = 56.5725 \)
After a few iterations, you will find that the value stabilizes around 56.57, which is a good approximation for the square root of 3200.
Using Linear Interpolation
Another method to approximate square roots is linear interpolation between two known squares. For instance, we know:
- \(50^2 = 2500\)
- \(60^2 = 3600\)
The square root of 3200 lies between 50 and 60. To estimate more precisely:
- Find the proportion of the way 3200 is between 2500 and 3600:
\( proportion = \frac{700}{1100} = 0.636 \) - Apply this proportion to the interval between 50 and 60:
\( estimate = 50 + 6.36 = 56.36 \)
Using linear interpolation, we get an estimate of approximately 56.36 for the square root of 3200.
Both methods provide a means to approximate square roots, and with practice, they can be performed quickly and with reasonable accuracy.
Calculating the Square Root of 3200
To calculate the square root of 3200, we can use a few different methods, including prime factorization, the long division method, and approximations. Below is a detailed, step-by-step guide using these methods:
Prime Factorization Method
The prime factorization of 3200 involves breaking down the number into its prime factors:
- First, find the prime factors of 3200: 3200 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5.
- Group the factors into pairs: (2 × 2), (2 × 2), (2 × 2), and (5 × 5), leaving one unpaired 2.
- Take one factor from each pair and multiply them together: 2 × 2 × 2 × 5 = 40.
- Combine this product with the square root of the remaining unpaired factor: 40√2.
Therefore, the simplified form of the square root of 3200 is 40√2, which is approximately 56.568542494924 in decimal form.
Long Division Method
The long division method is another way to find the square root of a number. Here are the steps to find the square root of 3200 using long division:
- Pair the digits of the number starting from the decimal point: 32 | 00 | 00.
- Find the largest number whose square is less than or equal to the first pair (32). This number is 5 because 5² = 25.
- Subtract 25 from 32 to get 7, and bring down the next pair (00), making the new number 700.
- Double the divisor (5) to get 10, and find a digit (D) such that 10D × D is less than or equal to 700. The digit is 6 because 106 × 6 = 636.
- Continue this process to get more decimal places as needed.
Using this method, the square root of 3200 is approximately 56.568542494924.
Approximating the Square Root
For a quick approximation, you can use the fact that 3200 is close to 3600, which is a perfect square (60²). Thus, the square root of 3200 is slightly less than 60.
To refine the approximation, you can use the average of 56 and 57 as a starting point:
- Since 56² = 3136 and 57² = 3249, and 3200 lies between these values, we can use the average: (56 + 57) / 2 = 56.5.
- Refine further by checking 56.5² = 3192.25, which is closer but slightly less than 3200, so the actual value is a bit more than 56.5.
The exact value calculated more precisely is 56.568542494924.
Applications of Square Roots
Understanding how to calculate square roots is useful in various fields such as engineering, physics, and finance. For example, if you have a square with an area of 3200 square units, the side length of the square would be the square root of 3200, which is approximately 56.57 units.
Conclusion
By using methods such as prime factorization and long division, we can accurately determine that the square root of 3200 is approximately 56.568542494924. This understanding not only aids in mathematical computations but also has practical applications in everyday problems and professional fields.
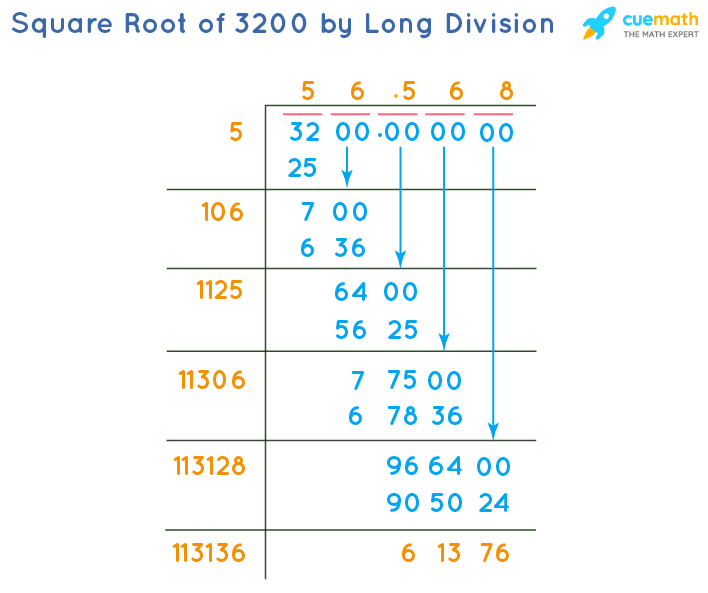
Step-by-Step Guide to Finding the Square Root of 3200
Finding the square root of 3200 can be done using several methods. Here, we will focus on two popular techniques: Prime Factorization and Long Division.
1. Prime Factorization Method
First, factorize 3200 into its prime factors:
- 3200 = 32 × 100
- 32 = 2 × 2 × 2 × 2 × 2 = 25
- 100 = 10 × 10 = (2 × 5) × (2 × 5) = 22 × 52
- Therefore, 3200 = 27 × 52
Next, group the prime factors into pairs:
- 3200 = (22 × 22 × 22) × 2 × 52
- 3200 = (2 × 2) × (2 × 2) × (2 × 2) × (2 × 5) × 5
- 3200 = (23 × 5) × (2 × 2 × 5)
Take the square root of each pair of prime factors:
- √3200 = √(26 × 2 × 52) = (23 × 5) × √(2)
- √3200 = 40√2
- √3200 ≈ 40 × 1.414 ≈ 56.568
2. Long Division Method
Start by pairing the digits of the number from right to left (32 | 00).
Find the largest number whose square is less than or equal to 32. This number is 5 (since 52 = 25 and 62 = 36).
Subtract 25 from 32 to get 7. Bring down the next pair of digits (00), making the new number 700.
Double the divisor (5 × 2 = 10) and determine how many times it fits into the new number. This is determined by trial and error.
Continue this process to get more decimal places. After several steps, you will find that √3200 ≈ 56.568.
Summary
Both the Prime Factorization and Long Division methods yield the square root of 3200 as approximately 56.568. Each method has its own steps and can be used depending on whether you need an exact form or a decimal approximation.
Prime Factorization of 3200
The prime factorization of a number is the process of expressing it as the product of its prime factors. To find the prime factors of 3200, we repeatedly divide it by the smallest prime number until we reach 1. Here is a detailed step-by-step guide to the prime factorization of 3200:
- Start with the number 3200.
- Divide 3200 by the smallest prime number, which is 2:
- 3200 ÷ 2 = 1600
- Continue dividing by 2 until you cannot divide evenly by 2 anymore:
- 1600 ÷ 2 = 800
- 800 ÷ 2 = 400
- 400 ÷ 2 = 200
- 200 ÷ 2 = 100
- 100 ÷ 2 = 50
- 50 ÷ 2 = 25
- Since 25 is not divisible by 2, move to the next smallest prime number, which is 5:
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
After all these divisions, we get the prime factors of 3200:
Prime factors of 3200 are: 2, 2, 2, 2, 2, 2, 2, 5, 5.
In exponential form, the prime factorization of 3200 is:
\[
3200 = 2^7 \times 5^2
\]
This means that 3200 can be expressed as the product of 2 raised to the power of 7 and 5 raised to the power of 2. This method of factorization is useful for understanding the fundamental building blocks of a number, which can be applied in various areas of mathematics and real-world problem solving.
| Step | Operation | Result |
|---|---|---|
| 1 | 3200 ÷ 2 | 1600 |
| 2 | 1600 ÷ 2 | 800 |
| 3 | 800 ÷ 2 | 400 |
| 4 | 400 ÷ 2 | 200 |
| 5 | 200 ÷ 2 | 100 |
| 6 | 100 ÷ 2 | 50 |
| 7 | 50 ÷ 2 | 25 |
| 8 | 25 ÷ 5 | 5 |
| 9 | 5 ÷ 5 | 1 |
This table summarizes the steps taken to achieve the prime factorization of 3200.
Exact Form of the Square Root of 3200
To express the square root of 3200 in its exact form, we start with the prime factorization of 3200.
- 3200 can be factored into its prime factors: \(3200 = 2^6 \times 5^2\).
- The square root of a product of primes can be expressed as the product of the square roots of the individual factors.
Thus, we have:
\[ \sqrt{3200} = \sqrt{2^6 \times 5^2} \]
This can be simplified by separating the factors:
\[ \sqrt{3200} = \sqrt{2^6} \times \sqrt{5^2} \]
Taking the square root of each prime factor:
\[ \sqrt{2^6} = 2^3 = 8 \]
\[ \sqrt{5^2} = 5 \]
Multiplying these results together gives us the exact form of the square root of 3200:
\[ \sqrt{3200} = 8 \times 5 = 40\sqrt{2} \]
Therefore, the exact form of the square root of 3200 is \( 40\sqrt{2} \).
Decimal Approximation of the Square Root of 3200
To find the decimal approximation of the square root of 3200, we can use various methods, such as a calculator or numerical estimation techniques. The decimal approximation provides a practical value that can be used in various applications.
Here is the step-by-step process to approximate the square root of 3200:
- First, recognize that 3200 is not a perfect square, so its square root will be an irrational number.
- Using a calculator or an online tool, you can directly find the decimal value. The square root of 3200 is approximately 56.5685424949.
- For manual approximation, you can use methods such as the long division method or iterative methods like the Newton-Raphson method. However, these are more complex and typically done with the aid of a calculator for higher precision.
Here is a table showing the square root of 3200 up to various decimal places for reference:
| Decimal Places | Value |
|---|---|
| 1 | 56.6 |
| 2 | 56.57 |
| 3 | 56.569 |
| 4 | 56.5685 |
| 5 | 56.56854 |
| 6 | 56.568542 |
| 7 | 56.5685425 |
| 8 | 56.56854249 |
| 9 | 56.568542495 |
Using these methods, you can find a highly precise decimal approximation for the square root of 3200, suitable for various mathematical and practical applications.

Applications of Square Roots in Real Life
Square roots have a wide range of applications in various fields of everyday life, ranging from science and engineering to finance and technology. Here are some practical uses of square roots:
-
Finance:
Square roots are used to calculate stock market volatility, which measures how much a stock’s price swings over time. Investors use this information to assess the risk of investments. For instance, the standard deviation, a key metric in finance, is derived using the square root of the variance of stock returns.
-
Architecture and Engineering:
Square roots are essential in determining the natural frequency of structures like buildings and bridges. This helps engineers predict how structures will respond to different loads, such as wind or traffic, ensuring safety and stability.
-
Science:
In physics, square roots are used to calculate quantities like the velocity of moving objects, the amount of radiation absorbed by materials, and the intensity of sound waves. These calculations are crucial for scientific research and technological advancements.
-
Statistics:
Square roots are fundamental in statistics for calculating the standard deviation, which measures the dispersion of a data set. This helps statisticians understand data variability and make informed decisions based on statistical analyses.
-
Geometry:
In geometry, square roots are used to compute the area and perimeter of shapes and to solve problems involving right triangles through the Pythagorean theorem. For example, the length of the hypotenuse in a right triangle is found using the square root of the sum of the squares of the other two sides.
-
Computer Science:
Square roots are used in computer programming for various applications, including encryption algorithms, image processing, and game physics. For example, encryption algorithms use modular arithmetic and square roots to secure data transmissions.
-
Navigation:
In navigation, square roots are used to calculate distances between points on a map or globe. Pilots use these calculations to determine the distance and direction between locations, aiding in accurate navigation.
-
Electrical Engineering:
Square roots are crucial in electrical engineering for calculating power, voltage, and current in circuits. These calculations are vital for designing and developing electrical systems, such as power grids and communication networks.
-
Photography:
The aperture of a camera lens is controlled using f-numbers, which are ratios involving the square root of the lens diameter. Adjusting the f-number changes the amount of light entering the camera, affecting image exposure.
These examples illustrate the versatility and importance of square roots in various aspects of daily life, highlighting their significance beyond academic contexts.
Common Mistakes and Misconceptions
Understanding square roots is crucial, but it's easy to make mistakes along the way. Here are some common errors and misconceptions to watch out for:
-
Assuming Linearity:
A common mistake is to assume that operations on sums work the same for all functions. For example, \(\sqrt{x + y} \ne \sqrt{x} + \sqrt{y}\). This is a misconception because square roots do not distribute over addition.
-
Incorrect Simplification:
Another error is simplifying expressions incorrectly. For instance, \(\sqrt{a^2} = a\) is only true if \(a \geq 0\). If \(a\) is negative, the correct simplification is \(\sqrt{a^2} = |a|\).
-
Ignoring Negative Roots:
When solving equations like \(x^2 = 9\), it's crucial to remember both positive and negative solutions. Therefore, \(x = 3\) and \(x = -3\).
-
Misapplying Properties:
Students often misuse properties of exponents and radicals. For example, \((\sqrt{x})^2 = x\) is correct, but \(\sqrt{x^2} = |x|\), not \(x\).
-
Canceling Errors:
Be cautious when canceling terms. For instance, in the expression \(\frac{\sqrt{a} \cdot \sqrt{b}}{\sqrt{a}}\), you can cancel \(\sqrt{a}\) only if \(a \ne 0\).
-
Incorrect Radical Operations:
Radicals should be manipulated carefully. For example, \(\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}\), but \(\sqrt{a} + \sqrt{b} \ne \sqrt{a+b}\).
By being aware of these common pitfalls, you can avoid errors and deepen your understanding of square roots.
Advanced Topics in Square Roots
Square roots are not just limited to basic arithmetic and simple calculations. They play a crucial role in various advanced mathematical concepts and applications. In this section, we will explore some of these advanced topics to provide a deeper understanding of square roots.
1. Irrational Numbers and Square Roots
Square roots often result in irrational numbers, which cannot be expressed as a simple fraction. For example, the square root of 2 ( √2 ) is an irrational number. These numbers are significant in number theory and have unique properties.
2. Complex Numbers and Square Roots
Square roots are not limited to real numbers. When dealing with negative numbers, we use complex numbers. For instance, the square root of -1 is represented as 'i', where \( i^2 = -1 \). This concept is fundamental in complex analysis and electrical engineering.
3. Quadratic Equations
Square roots are integral in solving quadratic equations of the form \( ax^2 + bx + c = 0 \). The quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) uses square roots to find the solutions for x.
4. Differential Equations
Square roots appear in the solutions of various differential equations. For example, the characteristic equation of a second-order linear differential equation often involves square roots to determine the nature of the solution (real or complex roots).
5. Eigenvalues and Eigenvectors
In linear algebra, square roots are used in the calculation of eigenvalues and eigenvectors. The characteristic equation of a matrix involves finding the roots of a polynomial, which often requires taking square roots.
6. Geometry and Trigonometry
Square roots are essential in geometry, particularly in calculating distances using the Pythagorean theorem. In trigonometry, they are used to determine the sides of right triangles and in the derivation of trigonometric identities.
7. Calculus
In calculus, square roots appear in the computation of limits, derivatives, and integrals. For example, the limit definition of the derivative involves expressions with square roots, and integrals often require techniques to simplify square root expressions.
8. Mathematical Proofs
Square roots are frequently encountered in mathematical proofs, such as proving the irrationality of certain numbers, the convergence of series, and the properties of functions.
9. Numerical Methods
Various numerical methods, such as the Newton-Raphson method, are used to approximate square roots. These methods are essential in computational mathematics for solving equations that do not have closed-form solutions.
10. Special Functions
Square roots are involved in the definition and properties of special functions like Bessel functions, Legendre polynomials, and Hermite polynomials. These functions appear in solutions to differential equations in physics and engineering.
11. Applications in Physics
In physics, square roots are used in equations describing wave functions, quantum mechanics, and general relativity. For instance, the Schrödinger equation and the equations for time dilation in relativity involve square roots.
Understanding these advanced topics provides a comprehensive view of the significance and applications of square roots in higher mathematics and various scientific fields.
Square Roots in Higher Mathematics
In higher mathematics, the concept of square roots extends beyond the basic operations and involves complex numbers, algebraic structures, and advanced calculus. Here are some advanced topics related to square roots:
- Complex Numbers and Imaginary Roots:
When dealing with negative numbers, square roots introduce the concept of imaginary numbers. The square root of a negative number is represented using the imaginary unit \(i\), where \(i = \sqrt{-1}\). For example, the square root of -3200 is expressed as \( \sqrt{-3200} = 56.568i \).
- Square Roots in Linear Algebra:
In linear algebra, square roots are used in various matrix operations. The concept of the matrix square root involves finding a matrix \(B\) such that \(B^2 = A\), where \(A\) is a given matrix. This is important in solving systems of linear equations and in the study of eigenvalues and eigenvectors.
- Square Roots in Differential Equations:
In solving differential equations, especially those involving oscillatory motion, the square root function appears in the characteristic equation solutions. For example, the solution to the differential equation \(ay'' + by' + cy = 0\) often involves terms of the form \(e^{\lambda t}\), where \( \lambda \) is derived from the square roots of the characteristic equation's roots.
- Newton's Method for Approximating Square Roots:
Newton's method is an iterative numerical technique used to approximate the square root of a number. Given an initial guess \(x_0\), the method uses the iteration formula:
\[
x_{n+1} = \frac{1}{2}\left(x_n + \frac{S}{x_n}\right)
\]
where \(S\) is the number whose square root is being approximated. This method converges quickly to the accurate value of the square root. - Square Roots in Complex Analysis:
In complex analysis, the square root function is a multi-valued function. For a complex number \(z = re^{i\theta}\), the principal square root is given by \( \sqrt{z} = \sqrt{r}e^{i\theta/2} \). This representation is crucial in understanding complex functions and their behaviors.
- Applications in Quantum Mechanics:
Square roots are also pivotal in quantum mechanics, particularly in wave functions and probability amplitudes. The normalization of wave functions often involves square root calculations to ensure the total probability is one.

Practice Problems and Solutions
Practicing square root problems helps in understanding the concept better and enhances problem-solving skills. Below are some practice problems along with their step-by-step solutions.
Problem 1: Solve for x in the equation \( x^2 - 3200 = 0 \)
Solution:
- Start with the given equation: \( x^2 - 3200 = 0 \)
- Add 3200 to both sides: \( x^2 = 3200 \)
- Take the square root of both sides: \( x = \pm \sqrt{3200} \)
- Since \( \sqrt{3200} \approx 56.57 \), the solutions are \( x = 56.57 \) and \( x = -56.57 \).
Problem 2: Find the length of the side of a cube if its surface area is 19200 square inches.
Solution:
- Let \( a \) be the length of a side of the cube.
- Surface area of a cube is given by \( 6a^2 = 19200 \).
- Divide both sides by 6: \( a^2 = 3200 \).
- Take the square root of both sides: \( a = \sqrt{3200} \).
- Since \( \sqrt{3200} \approx 56.57 \), the side length is \( a = 56.57 \) inches.
Problem 3: Determine the length of a side of a square with an area of 3200 square inches.
Solution:
- Let \( s \) be the length of a side of the square.
- Area of a square is given by \( s^2 = 3200 \).
- Take the square root of both sides: \( s = \sqrt{3200} \).
- Since \( \sqrt{3200} \approx 56.57 \), the side length is \( s = 56.57 \) inches.
Problem 4: Simplify the expression \( \sqrt{3200} \).
Solution:
- Prime factorize 3200: \( 3200 = 2^7 \times 5^2 \).
- Pair the prime factors: \( \sqrt{3200} = \sqrt{(2^7) \times (5^2)} = 2^3 \times 5 \times \sqrt{2} = 40\sqrt{2} \).
- The simplified form is \( 40\sqrt{2} \).
Problem 5: Calculate \( 4 + 17\sqrt{3200} \).
Solution:
- First, find the value of \( \sqrt{3200} \): \( \sqrt{3200} \approx 56.57 \).
- Substitute the value into the expression: \( 4 + 17 \times 56.57 \).
- Calculate the multiplication: \( 17 \times 56.57 = 961.69 \).
- Add 4 to the result: \( 4 + 961.69 = 965.69 \).
- Thus, \( 4 + 17\sqrt{3200} \approx 965.69 \).
Frequently Asked Questions (FAQs)
Here are some commonly asked questions about the square root of 3200:
- What is the Value of the Square Root of 3200?
- Why is the Square Root of 3200 an Irrational Number?
- How do You Simplify the Square Root of 3200?
- Prime factorize 3200: 2^7 × 5^2
- Group the factors in pairs: (2^6) × (2 × 5^2)
- Take one factor from each pair: 2^3 × 5 = 40
- The simplified form is 40√2
- What is the Square Root of -3200?
- What is the Square Root of 3200 in Decimal Form?
- What is the Square of the Square Root of 3200?
- Evaluate 4 + 17√3200
- Calculate √3200 ≈ 56.568
- Multiply 17 by 56.568: 17 × 56.568 = 961.656
- Add 4 to the result: 4 + 961.656 = 965.656
The square root of 3200 is approximately 56.56854.
The square root of 3200 is irrational because its prime factorization (2^7 × 5^2) contains a prime number (2) with an odd exponent, leading to a non-terminating, non-repeating decimal.
To simplify √3200:
The square root of -3200 is an imaginary number, expressed as 56.568i, where i is the imaginary unit (√-1).
In decimal form, the square root of 3200 is approximately 56.56854.
The square of the square root of 3200 is 3200, i.e., (√3200)^2 = 3200.
Given 4 + 17√3200:
READ MORE:
Khám phá cách tính căn bậc hai của 3200 một cách chi tiết và dễ hiểu. Học các phương pháp khác nhau và ứng dụng thực tế của căn bậc hai.
Căn Bậc Hai của 3200 - Hướng Dẫn Toàn Diện














