Topic what is the square root of 30: Are you curious about the square root of 30? In this article, we explore what the square root of 30 is, its mathematical significance, and practical applications. Join us as we uncover the value of \( \sqrt{30} \) and understand its importance in various fields.
Table of Content
- Square Root of 30
- Introduction to Square Roots
- Understanding the Square Root of 30
- Mathematical Representation of Square Roots
- How to Calculate the Square Root of 30
- Properties of the Square Root of 30
- Decimal Approximation of the Square Root of 30
- Methods to Find the Square Root
- Using a Calculator for Square Roots
- Successive Approximation Method
- Applications of the Square Root of 30
- Real-world Examples
- Common Mistakes and Misconceptions
- Square Roots in Geometry and Algebra
- Importance of Understanding Square Roots
- Further Reading and Resources
- YOUTUBE:
Square Root of 30
The square root of 30 is an irrational number, which means it cannot be expressed as a simple fraction. It is a value that, when multiplied by itself, gives the number 30.
Mathematical Expression
The square root of 30 is denoted as:
$$\sqrt{30}$$
Approximate Value
The approximate value of the square root of 30 is:
$$\sqrt{30} \approx 5.477225575051661$$
Steps to Calculate
- Identify the perfect squares closest to 30. These are 25 and 36.
- Since \( \sqrt{25} = 5 \) and \( \sqrt{36} = 6 \), we know that \( \sqrt{30} \) is between 5 and 6.
- Use the method of successive approximations or a calculator to get a more precise value.
Properties
- Irrational Number: The square root of 30 cannot be exactly expressed as a fraction.
- Non-repeating Decimal: The decimal form of \( \sqrt{30} \) is non-terminating and non-repeating.
- Positive and Negative Roots: The square root of 30 has two values: \( +\sqrt{30} \) and \( -\sqrt{30} \).
Applications
The square root of 30 is used in various mathematical calculations, including those in geometry, algebra, and real-world problem-solving scenarios where an approximate value is sufficient.

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations that are essential in various fields, from basic arithmetic to advanced sciences. The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 30, denoted as \( \sqrt{30} \), is the value that satisfies the equation \( x^2 = 30 \).
Here is a step-by-step explanation of square roots:
- Definition: A square root of a number \( n \) is a number \( x \) such that \( x^2 = n \). Every positive number \( n \) has two square roots: \( \sqrt{n} \) (positive root) and \( -\sqrt{n} \) (negative root).
- Notation: The square root of a number is written using the radical symbol \( \sqrt{} \). For example, the square root of 30 is written as \( \sqrt{30} \).
- Properties:
- Non-negative Numbers: The square root of a non-negative number is also non-negative.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are integers.
- Irrational Numbers: The square root of numbers that are not perfect squares (like 30) are irrational numbers, meaning they cannot be expressed as simple fractions and have non-repeating, non-terminating decimal expansions.
- Calculating Square Roots: Square roots can be calculated using various methods, including:
- Prime Factorization: Decomposing a number into its prime factors can help identify its square roots.
- Estimation and Approximation: Finding two perfect squares between which the number lies and estimating the square root.
- Using Calculators: Modern calculators and computers can quickly find square roots to many decimal places.
Understanding square roots is crucial for solving quadratic equations, working with geometric shapes, and analyzing scientific data. The concept of square roots extends to complex numbers and higher mathematics, providing a foundation for more advanced studies.
Understanding the Square Root of 30
The square root of 30 is an interesting and important mathematical concept. It is an irrational number, meaning it cannot be exactly expressed as a simple fraction and its decimal representation is non-repeating and non-terminating.
To understand the square root of 30, let's explore its properties and methods of calculation:
- Definition: The square root of 30, denoted as \( \sqrt{30} \), is the number that, when multiplied by itself, equals 30. Mathematically, it satisfies the equation \( x^2 = 30 \).
- Decimal Approximation: Using a calculator, we find that:
$$\sqrt{30} \approx 5.477225575051661$$
This value is approximate because the true value is irrational. - Properties:
- Irrationality: Since 30 is not a perfect square, \( \sqrt{30} \) is an irrational number.
- Non-terminating Decimal: The decimal expansion of \( \sqrt{30} \) goes on forever without repeating.
- Methods to Calculate:
- Estimation: Identify the two perfect squares between which 30 lies. Since \( 5^2 = 25 \) and \( 6^2 = 36 \), we know that \( \sqrt{30} \) is between 5 and 6.
- Successive Approximation: Refine the estimate by finding averages:
- Estimate: \( 5.5^2 = 30.25 \). So, \( \sqrt{30} \) is slightly less than 5.5.
- Next, try 5.47: \( 5.47^2 \approx 29.9209 \). Thus, \( \sqrt{30} \) is a bit more than 5.47.
- Further refinement: \( 5.477^2 \approx 29.997529 \). This process continues to improve the accuracy.
- Calculator: Use a scientific calculator for a precise value.
Understanding the square root of 30 enhances comprehension of irrational numbers and their properties. This knowledge is applicable in various mathematical contexts, including geometry, algebra, and real-world problem-solving.
Mathematical Representation of Square Roots
Square roots are fundamental mathematical concepts represented using the radical symbol (√). The square root of a number is a value that, when multiplied by itself, yields the original number. For example, the square root of 30 is denoted as \( \sqrt{30} \).
To better understand the mathematical representation of square roots, consider the following steps:
- Radical Symbol: The symbol used to represent the square root is √, known as the radical sign. For any non-negative number \( x \), \( \sqrt{x} \) denotes its square root.
- Equation Form: The square root of a number \( n \) is a number \( x \) such that:
$$x^2 = n$$
For instance, for \( n = 30 \):$$x^2 = 30 \Rightarrow x = \sqrt{30}$$
- Positive and Negative Roots: Every positive number has two square roots: a positive and a negative. These are represented as \( \sqrt{n} \) and \( -\sqrt{n} \). For example:
$$\sqrt{30} \approx 5.477$$
$$-\sqrt{30} \approx -5.477$$
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are integers. For example:
$$\sqrt{25} = 5$$
- Irrational Numbers: When a number is not a perfect square, its square root is an irrational number. This means it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion. For example:
$$\sqrt{30} \approx 5.477225575051661$$
- Complex Numbers: The concept of square roots extends to negative numbers using complex numbers. The square root of a negative number is represented using the imaginary unit \( i \), where:
$$i = \sqrt{-1}$$
For example:$$\sqrt{-30} = \sqrt{30} \cdot i$$
Understanding the mathematical representation of square roots is essential for solving equations, analyzing functions, and exploring more advanced mathematical concepts. Square roots are widely used in geometry, algebra, calculus, and various real-world applications.
How to Calculate the Square Root of 30
Calculating the square root of 30 involves several methods, ranging from simple estimation to using a calculator. Below are detailed steps and techniques to find \( \sqrt{30} \).
- Estimation Method:
- Identify the perfect squares closest to 30. These are 25 (5²) and 36 (6²).
- Since \( \sqrt{25} = 5 \) and \( \sqrt{36} = 6 \), we know that \( \sqrt{30} \) is between 5 and 6.
- Estimate a midpoint: \( 5.5 \). Calculate \( 5.5^2 = 30.25 \). Since 30.25 is slightly more than 30, \( \sqrt{30} \) is slightly less than 5.5.
- Refine the estimate: Try 5.47. Calculate \( 5.47^2 \approx 29.9209 \). Since 29.9209 is slightly less than 30, \( \sqrt{30} \) is slightly more than 5.47.
- Further refinement can be done by trying values closer to 5.477 until the desired accuracy is achieved.
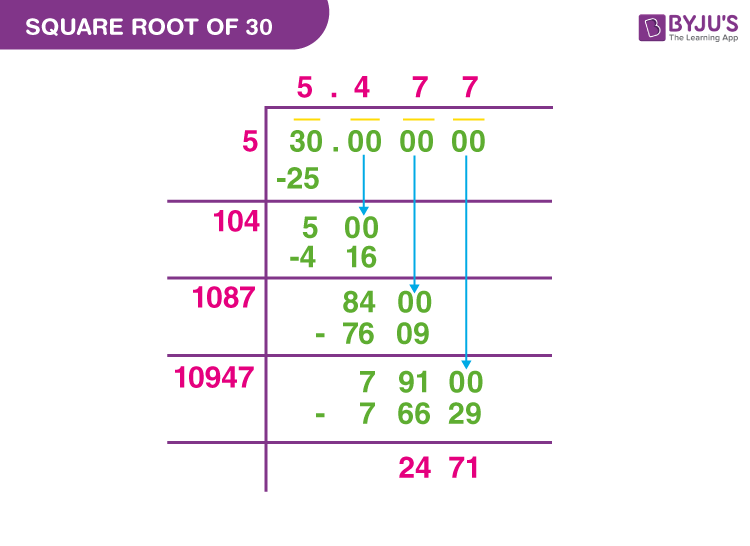
- Using Long Division Method:
- Pair the digits of 30 from right to left. Since 30 is a two-digit number, it is already paired.
- Find the largest number whose square is less than or equal to the first pair (30). This is 5, since \( 5^2 = 25 \).
- Write 5 above the bar. Subtract 25 from 30, giving a remainder of 5.
- Double the number above the bar (5), giving 10. Bring down a pair of zeros, making the dividend 500.
- Find the largest digit \( x \) such that \( 10x \cdot x \leq 500 \). This is 4, since \( 104 \cdot 4 = 416 \).
- Place 4 next to 5 above the bar, giving 5.4. Subtract 416 from 500, giving a remainder of 84.
- Continue this process to get more decimal places. Each step involves bringing down another pair of zeros and repeating the calculation.
- Using a Calculator:
- Enter the number 30 into the calculator.
- Press the square root (√) button.
- The calculator will display the square root of 30 as approximately 5.477225575051661.
- Using Newton's Method:
- Start with an initial guess. A reasonable guess for \( \sqrt{30} \) is 5.5.
- Use the formula:
$$x_{n+1} = \frac{1}{2} \left( x_n + \frac{30}{x_n} \right)$$
- Iterate using this formula:
- First iteration: \( x_1 = \frac{1}{2} \left( 5.5 + \frac{30}{5.5} \right) \approx 5.477272727 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 5.477272727 + \frac{30}{5.477272727} \right) \approx 5.477225576 \)
- Repeat the iterations until the desired accuracy is achieved.
By following these methods, you can accurately calculate the square root of 30, whether by estimation, long division, calculator use, or iterative approaches like Newton's Method.

Properties of the Square Root of 30
The square root of 30 has several interesting and important properties. These properties help us understand its behavior in various mathematical contexts and its significance in real-world applications.
- Irrational Number: The square root of 30, denoted as \( \sqrt{30} \), is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation is non-terminating and non-repeating.
- Decimal Approximation: The approximate value of \( \sqrt{30} \) is:
$$\sqrt{30} \approx 5.477225575051661$$
This value is often rounded to 5.477 for practical purposes. - Non-negative Value: By definition, the principal square root of 30 is non-negative. Therefore:
$$\sqrt{30} \geq 0$$
- Two Roots: Every positive number has two square roots: one positive and one negative. For 30, these roots are:
$$\sqrt{30} \approx 5.477$$
$$-\sqrt{30} \approx -5.477$$
- Square Property: The square of the square root of 30 returns the original number:
$$\left( \sqrt{30} \right)^2 = 30$$
- Relationship with Other Numbers: The square root of 30 lies between the square roots of 25 and 36:
$$\sqrt{25} = 5 \text{ and } \sqrt{36} = 6$$
Thus,$$5 < \sqrt{30} < 6$$
- Prime Factorization Insight: While 30 itself can be factored into prime numbers (2, 3, 5), its square root does not lead to a simple fractional result because none of the factors are perfect squares.
- Applications: The square root of 30 is used in various fields, including:
- Geometry: For calculating distances and areas.
- Physics: In formulas involving root mean square and other measurements.
- Engineering: In stress and strain calculations, among others.
- Statistics: In standard deviation and variance calculations.
Understanding these properties of the square root of 30 enhances our ability to apply mathematical principles in solving problems and conducting analyses across different disciplines.
Decimal Approximation of the Square Root of 30
The square root of 30 is an irrational number, meaning it cannot be exactly represented as a simple fraction and its decimal expansion is non-terminating and non-repeating. Here, we explore the decimal approximation of \( \sqrt{30} \) and how it can be calculated.
To find the decimal approximation of \( \sqrt{30} \), several methods can be used:
- Calculator Method:
Using a scientific calculator, you can directly find the square root of 30 by entering the number and pressing the square root (√) button. The calculator provides a precise decimal approximation:
$$\sqrt{30} \approx 5.477225575051661$$
For practical purposes, this value is often rounded to a few decimal places, such as 5.477. - Long Division Method:
This method provides a systematic way to find the square root of 30 manually. Below is a step-by-step explanation:
- Pair the digits of 30 from right to left. Since 30 has only two digits, it is considered one pair.
- Find the largest number whose square is less than or equal to 30. This is 5, since \( 5^2 = 25 \).
- Subtract 25 from 30, leaving a remainder of 5. Bring down a pair of zeros, making it 500.
- Double the current quotient (5), giving 10. Find the largest digit \( x \) such that \( 10x \cdot x \leq 500 \). This is 4, since \( 104 \cdot 4 = 416 \).
- Subtract 416 from 500, leaving a remainder of 84. Bring down another pair of zeros to make it 8400, and continue the process to add more decimal places.
- Successive Approximation:
This iterative method refines the estimate of \( \sqrt{30} \) through averaging:
- Start with an initial guess, such as 5.5.
- Apply the formula:
$$x_{n+1} = \frac{1}{2} \left( x_n + \frac{30}{x_n} \right)$$
- First iteration: \( x_1 = \frac{1}{2} \left( 5.5 + \frac{30}{5.5} \right) \approx 5.477272727 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 5.477272727 + \frac{30}{5.477272727} \right) \approx 5.477225576 \)
- Continue iterating until the desired level of accuracy is achieved.
These methods illustrate how the decimal approximation of the square root of 30 can be found with different levels of precision. Understanding this process is important for applications requiring precise calculations, such as engineering, physics, and computer science.
Methods to Find the Square Root
Finding the square root of a number is a fundamental mathematical operation. There are several methods to determine the square root of a number, such as 30. These methods range from simple estimation techniques to more precise algorithms. Here, we will explore some of the most common methods:
- Estimation Method:
This method involves identifying the perfect squares closest to the number in question. For example:
- Determine the perfect squares surrounding 30: \( 25 \) (since \( 5^2 = 25 \)) and \( 36 \) (since \( 6^2 = 36 \)).
- Since \( \sqrt{25} = 5 \) and \( \sqrt{36} = 6 \), we know that \( \sqrt{30} \) is between 5 and 6.
- Estimate a value between 5 and 6. For instance, try 5.5. Calculate \( 5.5^2 = 30.25 \). Since 30.25 is slightly more than 30, \( \sqrt{30} \) is slightly less than 5.5.
- Long Division Method:
This method is a manual technique to find more precise square roots. Here is the step-by-step process:
- Pair the digits of the number from right to left. For 30, it is already paired as 30.
- Find the largest number whose square is less than or equal to 30. This is 5, since \( 5^2 = 25 \).
- Write 5 above the bar and subtract 25 from 30, leaving a remainder of 5.
- Bring down a pair of zeros, making the dividend 500.
- Double the number above the bar (5), giving 10. Find the largest digit \( x \) such that \( 10x \cdot x \leq 500 \). This is 4, since \( 104 \cdot 4 = 416 \).
- Write 4 next to 5 above the bar, making 5.4. Subtract 416 from 500, leaving a remainder of 84.
- Bring down another pair of zeros, making it 8400, and continue the process to add more decimal places.
- Calculator Method:
- Enter the number 30 into a scientific calculator.
- Press the square root (√) button.
- The calculator will display the square root of 30 as approximately 5.477225575051661.
- Newton's Method (Iterative Method):
This method, also known as the Newton-Raphson method, is an iterative technique that refines the estimate of the square root:
- Start with an initial guess. A reasonable guess for \( \sqrt{30} \) is 5.5.
- Apply the iterative formula:
$$x_{n+1} = \frac{1}{2} \left( x_n + \frac{30}{x_n} \right)$$
- First iteration: \( x_1 = \frac{1}{2} \left( 5.5 + \frac{30}{5.5} \right) \approx 5.477272727 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 5.477272727 + \frac{30}{5.477272727} \right) \approx 5.477225576 \)
- Continue iterating until the desired level of accuracy is achieved.
- Babylonian Method:
Also known as Heron's method, this is another iterative approach similar to Newton's method:
- Start with an initial guess \( x_0 \). A common starting point for \( \sqrt{30} \) is 6.
- Use the formula:
$$x_{n+1} = \frac{1}{2} \left( x_n + \frac{30}{x_n} \right)$$
- Iterate the process until the value stabilizes:
- First iteration: \( x_1 = \frac{1}{2} \left( 6 + \frac{30}{6} \right) = 5.5 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 5.5 + \frac{30}{5.5} \right) \approx 5.477272727 \)
- Continue the iterations to reach the desired precision.
These methods provide a variety of ways to find the square root of 30, each with different levels of precision and complexity. Whether using a simple calculator or performing manual calculations, understanding these techniques is essential for solving mathematical problems involving square roots.
Using a Calculator for Square Roots
Calculating the square root of 30 using a calculator is a straightforward process. Follow these steps to obtain the result:
-
Turn on your calculator. Ensure it is in standard mode, not in scientific or programming mode, unless you are using a scientific calculator which should be in normal operation mode.
-
Locate the square root button. This is often represented by the symbol √ or may be found as a second function of another key. On some calculators, you might need to press the "2nd" or "Shift" button to access the square root function.
-
Press the square root button (√). If the calculator requires you to input the number first, enter 30 and then press the square root button. Otherwise, press the square root button first and then enter 30.
-
Read the result displayed on the calculator screen. The square root of 30 is approximately 5.477225575051661.
Using a scientific calculator, you might find additional features such as:
Memory functions to store and recall the result for further calculations.
Options to change the display format to scientific notation if the result has many decimal places.
Capability to perform successive operations without clearing the result from the screen.
Here is a sample table showing the process on different types of calculators:
| Calculator Type | Step-by-Step Instructions |
|---|---|
| Basic Calculator | Enter "30", press "√" |
| Scientific Calculator | Press "√", enter "30", or enter "30", press "√" |
| Graphing Calculator | Enter "30", press "√" or use the calculator's built-in functions to compute the square root |
Using these steps and understanding the functionality of your specific calculator will help you accurately find the square root of any number, including 30, quickly and efficiently.
Successive Approximation Method
The successive approximation method is a manual technique to find the square root of a number, such as 30. This method involves a series of steps that progressively get closer to the exact square root. Here's a detailed guide on how to use this method to approximate the square root of 30:
Initial Estimate: Start with an initial guess. A good starting point for √30 is 5.5 since it is close to the actual value.
First Approximation: Divide the number 30 by the initial guess. In this case, 30 ÷ 5.5 = 5.4545.
Averaging: Take the average of the initial guess and the result from step 2. This gives (5.5 + 5.4545) / 2 = 5.4773.
Second Approximation: Repeat steps 2 and 3 using the new value. Divide 30 by the new approximation: 30 ÷ 5.4773 ≈ 5.4772.
Further Refinement: Take the average of the previous approximation and the result from step 4. This gives (5.4773 + 5.4772) / 2 = 5.47725.
Iteration: Continue this process of dividing and averaging until the value stabilizes. After a few iterations, the approximations should converge to a value close to the actual square root.
Using this method, we find that the square root of 30 is approximately 5.477, rounded to three decimal places. This technique is helpful for understanding the concept of square roots and for manual calculations without a calculator.
Here’s a summary in tabular form:
| Step | Operation | Result |
|---|---|---|
| Initial Guess | - | 5.5 |
| First Division | 30 ÷ 5.5 | 5.4545 |
| First Average | (5.5 + 5.4545) / 2 | 5.4773 |
| Second Division | 30 ÷ 5.4773 | 5.4772 |
| Second Average | (5.4773 + 5.4772) / 2 | 5.47725 |
By iterating through these steps, the approximation becomes more accurate, demonstrating the effectiveness of the successive approximation method.
Applications of the Square Root of 30
The square root of 30, approximately 5.477, finds applications in various fields such as science, engineering, finance, and daily life. Here are some notable examples:
-
Geometry and Architecture:
In geometry, the square root of 30 can be used to calculate the lengths of sides in geometric shapes where 30 is the area. For instance, if a square has an area of 30 square units, each side length is approximately
\(\sqrt{30}\) units. In architecture, square roots help in determining dimensions and structural load calculations. -
Physics:
Square roots are used to calculate physical quantities like velocities and forces. For example, if a formula involves a term where the variable is squared, solving for the variable requires the square root. In motion and mechanics, such calculations are common.
-
Finance:
In finance, square roots are used in risk assessment. For instance, the volatility of a stock, which measures how much its price varies, can be calculated using the square root of the variance of its returns. This helps investors in making informed decisions about the riskiness of stocks.
-
Statistics:
Square roots are fundamental in statistics for calculating standard deviation, which measures the dispersion of a dataset. If the variance of a dataset is 30, the standard deviation is
\(\sqrt{30}\) , helping in data analysis and interpretation. -
Computer Science and Cryptography:
Square roots are employed in algorithms for encryption and security. For instance, many cryptographic protocols use prime numbers and square roots to generate keys and ensure secure data transmission.
These applications highlight the importance of understanding the square root of 30 and its practical use in solving real-world problems across diverse fields.
Real-world Examples
The square root of 30 has various practical applications in different fields. Here are some real-world examples demonstrating its use:
- Finance: In finance, the square root function is used to calculate stock market volatility. For instance, to assess the risk of an investment, one might use the square root of the variance of stock returns.
- Geometry: The square root is frequently used in geometry, such as calculating the diagonal of a square. For example, the diagonal of a square with an area of 30 square units is determined using the formula \( d = \sqrt{A} \), where \( A \) is the area. Hence, the diagonal would be \( \sqrt{30} \).
- Engineering: Engineers use square roots in various calculations, such as determining the natural frequency of structures. For instance, the natural frequency \( f \) can be found using the formula \( f = \sqrt{\frac{k}{m}} \), where \( k \) is the stiffness and \( m \) is the mass of the structure.
- Physics: In physics, square roots are used to find the resultant vector in mechanics. For example, if a force vector has components \( F_x \) and \( F_y \), the magnitude \( F \) is given by \( F = \sqrt{F_x^2 + F_y^2} \). If \( F_x = 5 \) and \( F_y = 25 \), then \( F = \sqrt{5^2 + 25^2} = \sqrt{30} \).
- Computer Science: In computer graphics, square roots are used to calculate the distance between points. For example, the Euclidean distance between points \((x_1, y_1)\) and \((x_2, y_2)\) is given by \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). If the coordinates are such that the distance formula simplifies to \( \sqrt{30} \), this provides the required distance.
These examples illustrate how the square root of 30, while seemingly abstract, is crucial in many practical and theoretical applications across various disciplines.
Common Mistakes and Misconceptions
Understanding the square root of 30 involves avoiding common mistakes and misconceptions that can lead to incorrect calculations or misunderstandings. Here are some key points to be aware of:
-
Misinterpreting the Square Root Symbol:
One common error is misinterpreting the square root symbol (\(\sqrt{}\)). Students sometimes think that the square root of a number is the same as dividing the number by 2. For example, they might incorrectly believe that \(\sqrt{30} = 15\), which is not true. The correct value of \(\sqrt{30}\) is approximately 5.477.
-
Ignoring the Principle Square Root:
The square root symbol usually refers to the principal (positive) square root. Some might forget that square roots can be both positive and negative. While \(\sqrt{30} \approx 5.477\), there is also \(-\sqrt{30} \approx -5.477\). However, unless specifically stated, \(\sqrt{30}\) implies the positive root.
-
Confusing Square and Square Root:
Another misconception is confusing the operation of squaring a number and finding its square root. Squaring involves multiplying a number by itself (e.g., \(5^2 = 25\)), while finding the square root is the inverse operation (e.g., \(\sqrt{25} = 5\)).
-
Incorrect Approximation:
Some students might use an incorrect approximation of the square root. For example, using \(\sqrt{30} \approx 5.5\) instead of the more accurate value \(\sqrt{30} \approx 5.477\) can lead to significant errors in calculations.
-
Errors in Calculation Methods:
When using methods such as successive approximation or calculators, errors can occur if the steps are not followed carefully. It's important to follow each step precisely and check the results at each stage.
By being aware of these common mistakes and misconceptions, students can better understand and accurately calculate the square root of 30, ensuring their mathematical reasoning is sound and their results are reliable.

Square Roots in Geometry and Algebra
Square roots play a significant role in both geometry and algebra. Understanding how they function in these mathematical areas can provide deeper insights into various problems and solutions.
Square Roots in Geometry
In geometry, square roots are often used to determine the lengths of sides in right-angled triangles, especially when dealing with the Pythagorean theorem. The theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Mathematically, this is represented as:
\[c^2 = a^2 + b^2\]
Where \( c \) is the hypotenuse, and \( a \) and \( b \) are the other two sides. To find the length of the hypotenuse, you take the square root of the sum of the squares of the other two sides:
\[c = \sqrt{a^2 + b^2}\]
For example, if \( a = 3 \) and \( b = 4 \), then:
\[c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\]
Square Roots in Algebra
In algebra, square roots are used to solve quadratic equations, which are equations of the form \( ax^2 + bx + c = 0 \). One of the methods to solve these equations is by completing the square or using the quadratic formula:
\[x = \frac{{-b \pm \sqrt{b^2 - 4ac}}}{{2a}}\]
Here, the square root function is essential in finding the solutions (roots) of the quadratic equation. The term under the square root, \( b^2 - 4ac \), is called the discriminant and determines the nature of the roots.
Properties of Square Roots in Algebra
- Square roots can be both positive and negative since squaring either a positive or negative number yields a positive result. For example, both \( 3 \) and \( -3 \) are square roots of \( 9 \).
- The principal square root is the non-negative root and is usually denoted by the radical symbol \( \sqrt{} \). For instance, \( \sqrt{25} = 5 \), while the negative root is \( -\sqrt{25} = -5 \).
- Square roots can also be expressed in terms of exponents: \( \sqrt{x} = x^{1/2} \).
- When multiplying or dividing square roots, you can simplify them using properties of exponents. For example, \( \sqrt{a} \cdot \sqrt{b} = \sqrt{ab} \).
Square roots are fundamental in various mathematical problems and their applications in geometry and algebra highlight their importance in understanding and solving mathematical equations.
Importance of Understanding Square Roots
Understanding square roots is crucial for various reasons, extending beyond basic mathematical knowledge to practical applications in everyday life, science, and technology. Here are several key points highlighting the importance of understanding square roots:
- Fundamental Mathematical Concept:
Square roots are a basic concept in mathematics, essential for understanding more complex mathematical theories and operations. Mastery of square roots is foundational for progressing in algebra, geometry, and calculus.
- Geometry and Measurement:
Square roots are often used in geometry to determine the length of the sides of squares and right-angled triangles. For instance, the Pythagorean theorem, which is pivotal in many geometric calculations, involves square roots to find distances and lengths.
- Real-World Applications:
In real life, square roots are used in various fields such as architecture, engineering, and physics. For example, calculating the dimensions of an area, understanding the properties of waves in physics, and determining distances in navigation all involve square roots.
- Problem Solving:
Many real-world problems, such as finding the shortest distance between two points or the optimal use of materials, can be solved using square roots. This enhances critical thinking and problem-solving skills.
- Technology and Computer Science:
Square roots are integral in algorithms and computer graphics. Calculations involving square roots are used in developing simulations, animations, and solving equations in various software applications.
- Financial Calculations:
In finance, square roots are used in various calculations, including the computation of compound interest and risk assessment models. Understanding these can lead to better financial decisions and strategies.
- Scientific Research:
Square roots are frequently used in scientific research to analyze data, calculate standard deviations, and understand growth patterns. This application is vital in fields like biology, chemistry, and environmental science.
- Educational Development:
Learning about square roots fosters a deeper understanding of mathematical principles and enhances overall cognitive development. It prepares students for higher-level math and science courses, fostering analytical and logical thinking skills.
Further Reading and Resources
Understanding the square root of 30 and its properties is crucial for both academic purposes and practical applications. Here are some resources for further exploration and learning:
-
This calculator helps you find the square root of any number, including non-perfect squares, and provides step-by-step solutions for better understanding.
-
This tool reduces any square root to its simplest radical form and provides approximate values, making it a useful resource for both learning and teaching.
-
Explore various math topics and use their square root calculator for quick computations. This site is a comprehensive resource for students and educators alike.
-
Learn how to simplify the square root of 30 using prime factorization, and explore the decimal approximation of this irrational number.
-
This site offers detailed explanations on how to calculate the square root of 30, both manually and using various tools like calculators and spreadsheets.
-
Byju's provides a thorough explanation of the square root of 30, including its decimal form, radical form, and methods to calculate it using prime factorization and long division.
These resources will help you deepen your understanding of square roots and their applications. Whether you're a student, teacher, or enthusiast, these tools and guides offer valuable insights and practical tips for mastering the concept.
Square Root 30 - Hướng Dẫn Toàn Diện