What is the Square Root of 32 Simplified: A Comprehensive Guide

The square root of 32 can be simplified by breaking it down into its prime factors. Here's the process:

• First, factorize 32 into its prime factors: \( 32 = 2^5 \).
• Next, express the square root of 32 using these prime factors: \( \sqrt{32} = \sqrt{2^5} \).
• Then, separate the even power of the prime factors from the odd power: \( \sqrt{2^5} = \sqrt{2^4 \cdot 2} \).
• Since \( \sqrt{2^4} = 2^2 = 4 \), we can simplify this to: \( 4\sqrt{2} \).

Conclusion

The simplified form of the square root of 32 is \( 4\sqrt{2} \).

Thus, \( \sqrt{32} = 4\sqrt{2} \).

The process of simplifying the square root of 32 involves breaking it down into its simplest form. Simplifying square roots is a fundamental skill in mathematics that can make complex calculations more manageable. In this guide, we will explore the steps needed to simplify \( \sqrt{32} \) using prime factorization. This method will help you understand and master the technique of simplifying square roots.

Here are the steps we will follow:

• Factorize 32 into its prime factors.
• Group the prime factors into pairs.
• Simplify the expression by taking out the pairs as single numbers.

By the end of this guide, you will be able to simplify \( \sqrt{32} \) and apply the same method to other square roots with confidence.

Square roots are mathematical expressions used to determine a number that, when multiplied by itself, yields the original number. The square root of a number \( x \) is represented as \( \sqrt{x} \). For example, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).

In general, the process of finding a square root involves:

1. Identifying the original number.
2. Determining which number, when multiplied by itself, results in the original number.

Square roots can be classified into two main types:

• Perfect Squares: Numbers whose square roots are whole numbers. For instance, \( 1, 4, 9, 16, \) and \( 25 \) are perfect squares because their square roots are \( 1, 2, 3, 4, \) and \( 5 \), respectively.
• Non-Perfect Squares: Numbers whose square roots are not whole numbers. Examples include \( 2, 3, 5, 7, 8, \) and \( 10 \). These square roots are often irrational numbers, meaning they cannot be expressed as a simple fraction and their decimal form is non-repeating and non-terminating.

Understanding square roots is essential in various fields of mathematics, including algebra, geometry, and calculus. It provides a foundation for solving quadratic equations, analyzing geometric shapes, and understanding higher-level mathematical concepts.

Now that we have a basic understanding of square roots, let's move on to simplifying the square root of 32.

The prime factorization method is a technique used to simplify square roots by breaking down a number into its prime factors. This method is particularly useful for simplifying non-perfect squares, such as 32. Here’s a step-by-step guide to using the prime factorization method:

1. Identify the Prime Factors:

   First, factorize the number into its prime components. For 32, the prime factors are:

   • \( 32 \div 2 = 16 \)
   • \( 16 \div 2 = 8 \)
   • \( 8 \div 2 = 4 \)
   • \( 4 \div 2 = 2 \)
   • \( 2 \div 2 = 1 \)

   So, \( 32 = 2 \times 2 \times 2 \times 2 \times 2 = 2^5 \).

2. Group the Prime Factors:

   Next, group the prime factors into pairs. Each pair represents a squared number:

   • \( 2^5 = 2^4 \times 2 = (2^2)^2 \times 2 = 4^2 \times 2 \)
3. Simplify the Expression:

   Extract the squared numbers from under the square root:

   • \( \sqrt{32} = \sqrt{4^2 \times 2} = 4 \sqrt{2} \)

Thus, using the prime factorization method, we have simplified \( \sqrt{32} \) to \( 4 \sqrt{2} \). This method can be applied to other numbers to simplify their square roots as well.

Breaking down a number into its prime factors is an essential step in simplifying square roots. Prime factors are the prime numbers that multiply together to give the original number. Here is how we break down 32 into its prime factors:

1. Divide by the Smallest Prime Number:

   Start with the smallest prime number, which is 2, and divide 32 by 2:

   • \( 32 \div 2 = 16 \)
2. Continue Dividing by 2:

   Repeat the process of dividing by 2 until the quotient is 1:

   • \( 16 \div 2 = 8 \)
   • \( 8 \div 2 = 4 \)
   • \( 4 \div 2 = 2 \)
   • \( 2 \div 2 = 1 \)
3. List the Prime Factors:

   After completing the division, we find that the prime factors of 32 are all 2s:

   • \( 32 = 2 \times 2 \times 2 \times 2 \times 2 = 2^5 \)

So, the prime factorization of 32 is \( 2^5 \). This breakdown is crucial for the next steps in simplifying the square root of 32, as it allows us to group the factors into pairs and simplify the expression.

To simplify the square root of a number, it’s helpful to separate the even and odd powers of its prime factors. Here’s a step-by-step process to separate the even and odd powers of the prime factors of 32:

1. Prime Factorization:

   We already determined that the prime factorization of 32 is \( 2^5 \).

2. Identify Even and Odd Powers:

   In the prime factorization \( 2^5 \), identify the even and odd powers:

   • The power of 2 in \( 2^5 \) is 5. Since 5 is an odd number, we can separate it into \( 2^4 \) (an even power) and \( 2^1 \) (an odd power).
   • So, \( 2^5 = 2^4 \times 2^1 \).
3. Express the Even Powers:

   We know that \( 2^4 = (2^2)^2 = 4^2 \), so we can rewrite the expression as:

   • \( 2^5 = 4^2 \times 2 \).

By separating the even and odd powers, we can simplify the square root of 32 more easily. We have identified that \( 2^5 \) can be rewritten as \( 4^2 \times 2 \), setting us up for the next step in the simplification process.

Now that we have separated the even and odd powers of the prime factors, we can simplify the square root of 32. Here’s the step-by-step process:

1. Rewrite the Expression:

   We previously found that \( 2^5 = 4^2 \times 2 \). Thus, we can write the square root of 32 as:

   • \( \sqrt{32} = \sqrt{4^2 \times 2} \).
2. Apply the Square Root to Each Factor:

   Next, apply the square root to each factor separately. Using the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \), we get:

   • \( \sqrt{4^2 \times 2} = \sqrt{4^2} \times \sqrt{2} \).
3. Simplify the Square Root of the Even Power:

   The square root of \( 4^2 \) is 4 because \( \sqrt{4^2} = 4 \). Therefore, we have:

   • \( \sqrt{4^2} \times \sqrt{2} = 4 \times \sqrt{2} \).

So, the simplified form of the square root of 32 is \( 4\sqrt{2} \). By following these steps, we have taken the original expression \( \sqrt{32} \) and simplified it to \( 4\sqrt{2} \), making it easier to work with in mathematical calculations.

After following the steps to simplify the square root of 32, we arrive at the final simplified form. Here’s a summary of the process and the final result:

1. Prime Factorization:

   We started by breaking down 32 into its prime factors:

   • \( 32 = 2^5 \)
2. Separating Even and Odd Powers:

   Next, we separated the even and odd powers of the prime factors:

   • \( 2^5 = 4^2 \times 2 \)
3. Simplifying the Expression:

   Then, we applied the square root to each factor and simplified the expression:

   • \( \sqrt{32} = \sqrt{4^2 \times 2} = \sqrt{4^2} \times \sqrt{2} = 4 \times \sqrt{2} \)

Therefore, the final simplified form of the square root of 32 is:

\( \sqrt{32} = 4\sqrt{2} \)

This result shows that the square root of 32 can be expressed in a simpler form, making it easier to understand and use in further mathematical calculations. By breaking down the process step by step, we have clarified the method and demonstrated the final simplified form.

Simplifying square roots often involves finding the prime factorization of the number under the root and then simplifying based on pairs of prime factors. Here are some examples similar to simplifying the square root of 32:

• Square Root of 50

  1. Find the prime factors of 50: \(50 = 2 \times 5^2\)
  2. Identify pairs of prime factors: \(5^2\) can be taken out of the square root as a single 5
  3. Simplify: \(\sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2}\)

• Square Root of 72

  1. Find the prime factors of 72: \(72 = 2^3 \times 3^2\)
  2. Identify pairs of prime factors: \(2^2\) and \(3^2\) can be taken out of the square root as single 2 and 3
  3. Simplify: \(\sqrt{72} = \sqrt{2^3 \times 3^2} = 6\sqrt{2}\)

• Square Root of 18

  1. Find the prime factors of 18: \(18 = 2 \times 3^2\)
  2. Identify pairs of prime factors: \(3^2\) can be taken out of the square root as a single 3
  3. Simplify: \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\)

• Square Root of 45

  1. Find the prime factors of 45: \(45 = 3^2 \times 5\)
  2. Identify pairs of prime factors: \(3^2\) can be taken out of the square root as a single 3
  3. Simplify: \(\sqrt{45} = \sqrt{3^2 \times 5} = 3\sqrt{5}\)

Simplified square roots are used in various fields, including geometry, engineering, physics, and real-life problem-solving. Here are some applications where simplified square roots are particularly useful:

1. Geometry and Trigonometry

• Area and Perimeter Calculations: Simplifying square roots helps in calculating the dimensions of geometric shapes more easily. For example, the diagonal of a square with a side length of \( \sqrt{32} \) units can be simplified to \( 4\sqrt{2} \), making it easier to work with in further calculations.
• Trigonometric Functions: Many trigonometric functions involve square roots. Simplifying these roots helps in solving trigonometric equations and understanding the relationships between angles and side lengths in triangles.

2. Physics and Engineering

• Wave Functions: In physics, especially in quantum mechanics, wave functions often include square roots. Simplifying these roots aids in solving equations related to wave behavior and particle dynamics.
• Structural Analysis: Engineers use simplified square roots in the analysis of structures, such as beams and columns, to determine stress, strain, and other properties essential for safety and efficiency.

3. Real-Life Problem Solving

• Construction: In construction, calculating dimensions, areas, and volumes often involves square roots. Simplifying these roots ensures more accurate measurements and efficient material usage.
• Finance: Compound interest and other financial calculations sometimes involve square roots. Simplifying these roots can make it easier to understand and compute long-term financial outcomes.

4. Practical Examples

• Example 1: If you need to find the side length of a square with an area of 32 square units, you calculate \( \sqrt{32} = 4\sqrt{2} \). This helps in easily determining that each side is approximately 5.656 units long.
• Example 2: When calculating the distance a car travels at a speed of \( 4\sqrt{2} \) miles per hour for 2 hours, the simplified form makes it easier to find that the car covers 11.312 miles.

These applications highlight the importance of simplifying square roots in making complex calculations more manageable and accurate.

When simplifying the square root of 32, several common mistakes can occur. Being aware of these can help ensure accurate simplification and deepen your understanding of square roots. Here are some frequent errors and how to avoid them:

• Ignoring Prime Factorization:

  A common mistake is to skip the prime factorization step. Properly breaking down 32 into its prime factors (2 × 2 × 2 × 2 × 2) is crucial for accurate simplification.

• Incorrect Grouping of Factors:

  Misgrouping prime factors can lead to incorrect results. Remember, each pair of identical factors under the square root can be taken out as a single factor outside the square root. For example, (2 × 2) × (2 × 2) × 2 simplifies to 4√2, not √32.

• Overlooking the Radical Remainder:

  It's important not to forget any factors that cannot be paired. In the case of 32, one 2 remains under the square root after taking out pairs of 2s, resulting in 4√2.

• Misapplying Square Root Properties:

  Incorrectly applying properties of square roots, such as assuming √(a × b) = √a × √b in all contexts, can lead to errors. Ensure you apply properties correctly according to mathematical rules.

• Forgetting to Simplify Completely:

  Some may stop the simplification process too early. Ensure you simplify the square root to its most reduced form, such as simplifying √32 fully to 4√2.

To avoid these mistakes:

1. Always perform prime factorization and carefully group factors.
2. Review your work to ensure all factors are correctly simplified.
3. Practice regularly with different numbers to reinforce understanding.
4. Use visual aids or diagrams to grasp the concept of square roots more intuitively.

Avoiding these common mistakes not only leads to correct simplification of square roots like √32 but also enhances overall mathematical comprehension and problem-solving skills.

Here are some practice problems to help you master the process of simplifying square roots, similar to the simplification of the square root of 32:

1. Simplify the square root of 50.
   • Solution: Find the prime factors of 50 (2 × 5 × 5). Pair the prime factors: √50 = √(2 × 5 × 5) = 5√2.
2. Simplify the square root of 72.
   • Solution: Find the prime factors of 72 (2 × 2 × 2 × 3 × 3). Pair the prime factors: √72 = √(2 × 2 × 2 × 3 × 3) = 6√2.
3. Simplify the square root of 98.
   • Solution: Find the prime factors of 98 (2 × 7 × 7). Pair the prime factors: √98 = √(2 × 7 × 7) = 7√2.
4. Simplify the square root of 200.
   • Solution: Find the prime factors of 200 (2 × 2 × 2 × 5 × 5). Pair the prime factors: √200 = √(2 × 2 × 2 × 5 × 5) = 10√2.
5. Simplify the square root of 18.
   • Solution: Find the prime factors of 18 (2 × 3 × 3). Pair the prime factors: √18 = √(2 × 3 × 3) = 3√2.

These problems are designed to help you recognize patterns in the simplification process. Always look for pairs of prime factors to simplify the square root expression.

• What is the simplified form of the square root of 32?

  The simplified form of the square root of 32 is \(4\sqrt{2}\). This is derived from the prime factorization of 32, which is \(2 \times 2 \times 2 \times 2 \times 2\). Grouping the factors in pairs, we get \((2 \times 2) \times (2 \times 2) \times \sqrt{2} = 4\sqrt{2}\).

• Is the square root of 32 a rational number?

  No, the square root of 32 is not a rational number. The simplified form \(4\sqrt{2}\) contains \(\sqrt{2}\), which is an irrational number, making the entire expression irrational.

• How do you express the square root of 32 in exponential form?

  The square root of 32 can be expressed in exponential form as \(32^{1/2}\) or \(2^{5/2}\). This comes from the prime factorization and properties of exponents.

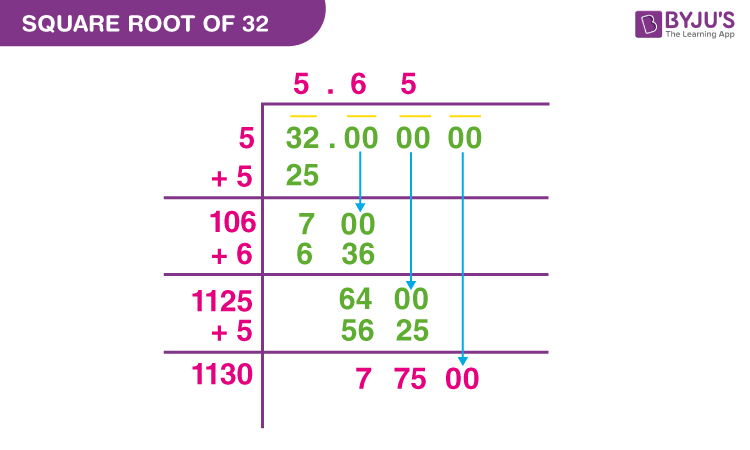
• What is the decimal value of the square root of 32?

  The approximate decimal value of the square root of 32 is 5.6569. This is obtained by calculating \(4 \times \sqrt{2}\), where \(\sqrt{2}\) is approximately 1.414.

• How is the square root of 32 used in real-world applications?

  Simplified square roots like \(4\sqrt{2}\) are often used in engineering, physics, and computer science to simplify complex calculations and express results more concisely. They are also used in geometry, particularly in problems involving right triangles and the Pythagorean theorem.