Topic square root of 3 over 2: The square root of 3 over 2 is a fundamental concept in mathematics, frequently appearing in geometry, trigonometry, and physics. This article explores its mathematical significance, practical applications, and interesting properties, offering a comprehensive guide to understanding and utilizing this important ratio in various fields.
Table of Content
- Understanding the Square Root of 3 Over 2
- Introduction to the Square Root of 3 Over 2
- Applications in Various Fields
- Trigonometric Significance
- Geometric Interpretations
- Role in Physics
- Properties and Characteristics
- Historical Context
- Practical Examples and Problems
- Common Misconceptions
- Advanced Mathematical Context
- Conclusion and Summary
- YOUTUBE: Hướng dẫn cộng 2 căn 3 và căn 3 một cách dễ hiểu và chi tiết. Video phù hợp cho những ai đang học toán và muốn hiểu rõ hơn về cách tính toán với căn bậc hai.
Understanding the Square Root of 3 Over 2
The expression is a mathematical term that can be used in various contexts, especially in geometry and trigonometry.
Mathematical Representation
The square root of 3 over 2 can be written as:
Decimal Approximation
The decimal approximation of is approximately 0.866. This value is often used in calculations where an exact fraction is not necessary.
Applications
- Trigonometry: In trigonometry, appears in the values of sine and cosine for 30° and 60° angles.
- Geometry: This expression is also found in various geometric calculations, especially those involving right triangles.
- Physics: In physics, it can appear in equations involving harmonic motion and waves.
Properties
| Property | Value |
| Exact Value | |
| Decimal Approximation | 0.866 |
| Appearance in Trigonometric Functions |
|

READ MORE:
Introduction to the Square Root of 3 Over 2
The expression represents a mathematical term that is commonly encountered in various fields of study.
This ratio is significant due to its frequent appearance in geometric and trigonometric contexts. Here, we will delve into its definition, properties, and applications.
Definition and Representation
- The square root of 3, denoted as , is an irrational number.
- When this value is divided by 2, it forms the ratio .
Properties
| Property | Details |
| Irrational Nature | The square root of 3 is irrational, meaning it cannot be expressed as a simple fraction. |
| Decimal Form | Approximately 0.866. |
Applications
- Trigonometry: Essential in the values of sine and cosine for 30° and 60° angles.
- Geometry: Appears in calculations involving equilateral triangles and other geometric figures.
- Physics: Used in various equations, particularly those involving wave mechanics and harmonic motion.
Understanding the square root of 3 over 2 provides valuable insights into many mathematical and scientific concepts, making it an important element in both theoretical and applied disciplines.
Applications in Various Fields
The square root of 3 over 2, represented as \( \frac{\sqrt{3}}{2} \), finds applications across various fields due to its unique mathematical properties. Here are some of the key applications:
- Trigonometry:
In trigonometry, \( \frac{\sqrt{3}}{2} \) frequently appears in the values of trigonometric functions for specific angles. For example, \( \sin(60^\circ) \) and \( \cos(30^\circ) \) both equal \( \frac{\sqrt{3}}{2} \). These values are crucial in solving problems involving right triangles and periodic phenomena.
- Geometry:
In geometry, \( \frac{\sqrt{3}}{2} \) is the height of an equilateral triangle with side length 1. This relationship is used to find the area and other properties of equilateral and isosceles triangles.
- Physics:
In physics, \( \frac{\sqrt{3}}{2} \) appears in calculations involving rotational motion and equilibrium. For instance, it can be used in determining the components of vectors in problems involving inclined planes and forces.
- Engineering:
Engineers utilize \( \frac{\sqrt{3}}{2} \) in analyzing mechanical systems, especially in the design of structures and understanding stresses in different components. It is also essential in electrical engineering, particularly in the study of alternating current circuits and phasor diagrams.
- Computer Science:
In computer graphics, \( \frac{\sqrt{3}}{2} \) is used in algorithms for rendering objects and simulations, particularly in the context of isometric projections and transformations.
- Environmental Science:
Environmental scientists use trigonometric values including \( \frac{\sqrt{3}}{2} \) in modeling natural phenomena such as wave patterns and in the analysis of climatic data.
These examples highlight the versatility and importance of \( \frac{\sqrt{3}}{2} \) in both theoretical and practical applications across various scientific and engineering disciplines.
Trigonometric Significance
The square root of 3 over 2, represented mathematically as \( \frac{\sqrt{3}}{2} \), holds significant importance in trigonometry. It is primarily associated with specific trigonometric functions and angles. Below, we explore its key roles and applications:
-
Sine of 60 Degrees:
One of the most notable occurrences of \( \frac{\sqrt{3}}{2} \) is in the sine function. Specifically, \( \sin 60^\circ = \sin \left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2} \). This value is derived from the properties of a 30-60-90 triangle, where the ratio of the side opposite the 60-degree angle to the hypotenuse is \( \frac{\sqrt{3}}{2} \).
-
Cosine of 30 Degrees:
Similarly, \( \frac{\sqrt{3}}{2} \) appears as the cosine of 30 degrees: \( \cos 30^\circ = \cos \left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2} \). This is again due to the properties of the 30-60-90 triangle, where the adjacent side of the 30-degree angle is \( \frac{\sqrt{3}}{2} \) of the hypotenuse.
-
Trigonometric Identities:
The value \( \frac{\sqrt{3}}{2} \) plays a critical role in various trigonometric identities and equations. For instance, the identity \( \sin^2 \theta + \cos^2 \theta = 1 \) holds true for angles where sine or cosine equals \( \frac{\sqrt{3}}{2} \). When \( \theta = 60^\circ \), we have \( \left(\frac{\sqrt{3}}{2}\right)^2 + \left(\frac{1}{2}\right)^2 = 1 \).
-
Unit Circle Representation:
On the unit circle, \( \frac{\sqrt{3}}{2} \) corresponds to the \( y \)-coordinate of the point at 60 degrees (or \( \frac{\pi}{3} \) radians) and the \( x \)-coordinate at 30 degrees (or \( \frac{\pi}{6} \) radians). This visualization aids in understanding the cyclical nature of sine and cosine functions.
-
Inverse Trigonometric Functions:
In problems involving inverse trigonometric functions, such as finding the angle whose sine is \( \frac{\sqrt{3}}{2} \), we solve \( \sin^{-1} \left(\frac{\sqrt{3}}{2}\right) = 60^\circ \) or \( \pi/3 \) radians. This is crucial for solving equations and understanding angles in different quadrants.
Understanding the trigonometric significance of \( \frac{\sqrt{3}}{2} \) is essential for solving many mathematical problems, particularly in the realms of geometry and calculus.
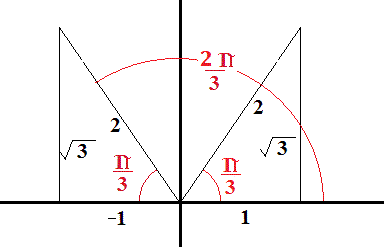
Geometric Interpretations
The square root of 3 over 2, denoted as \(\frac{\sqrt{3}}{2}\), appears frequently in geometry, particularly in the context of right triangles and regular polygons.
Here are some key geometric interpretations:
- Right Triangles:
In a 30-60-90 right triangle, the ratio of the lengths of the sides opposite these angles is 1 : \(\sqrt{3}\) : 2. Specifically, if the hypotenuse is 1, the side opposite the 30° angle (shortest side) is \(\frac{1}{2}\), and the side opposite the 60° angle (longer leg) is \(\frac{\sqrt{3}}{2}\).
Hypotenuse 1 Short Leg \(\frac{1}{2}\) Long Leg \(\frac{\sqrt{3}}{2}\) - Equilateral Triangles:
In an equilateral triangle, when an altitude is drawn, it creates two 30-60-90 triangles. The length of the altitude is \(\frac{\sqrt{3}}{2}\) times the side length of the equilateral triangle.
- Regular Hexagons:
A regular hexagon can be divided into six equilateral triangles. If the side length of the hexagon is \(s\), the distance from the center to any vertex (the radius of the circumscribed circle) is \(s\), and the distance from the center to the midpoint of any side is \(\frac{\sqrt{3}}{2} s\).
- Unit Circle:
On the unit circle, the coordinates of a point corresponding to a 30° angle (or \(\pi/6\) radians) from the positive x-axis are \((\frac{\sqrt{3}}{2}, \frac{1}{2})\). The x-coordinate \(\frac{\sqrt{3}}{2}\) represents the cosine of 30°.
Similarly, for a 60° angle (or \(\pi/3\) radians), the coordinates are \((\frac{1}{2}, \frac{\sqrt{3}}{2})\), where \(\frac{\sqrt{3}}{2}\) represents the sine of 60°.
These interpretations show the fundamental role of \(\frac{\sqrt{3}}{2}\) in various geometric contexts, especially in relation to right triangles, equilateral triangles, and regular polygons.
Role in Physics
The square root of 3 over 2, expressed as \( \frac{\sqrt{3}}{2} \), plays a significant role in various areas of physics. This mathematical constant often appears in formulas and equations that describe natural phenomena.
Here are some key applications of \( \frac{\sqrt{3}}{2} \) in physics:
-
Wave Mechanics:
In wave mechanics, the square root of 3 over 2 is used to describe the properties of certain waveforms. For instance, in the context of sinusoidal waves, it can be a part of the coefficients in the wave equation.
-
Optics:
In optics, \( \frac{\sqrt{3}}{2} \) is important in the analysis of light interference and diffraction patterns. It is often used in the calculations involving the angles and distances in diffraction gratings and optical paths.
-
Electricity and Magnetism:
The constant appears in the study of electromagnetic waves. It is used to describe the relative strengths of electric and magnetic fields in electromagnetic wave propagation, especially in the context of Maxwell's equations.
-
Crystallography:
In crystallography, \( \frac{\sqrt{3}}{2} \) is found in the geometry of crystal lattices, particularly in hexagonal close-packed structures. It helps determine the spacing and angles between atoms in a crystal.
-
Thermodynamics:
The constant also plays a role in statistical mechanics and thermodynamics. For example, in the calculation of root-mean-square speeds of particles in a gas, the factor \( \sqrt{3} \) often appears, indicating the isotropic distribution of particle velocities.
Understanding the applications of \( \frac{\sqrt{3}}{2} \) in these areas allows physicists to solve complex problems and develop more accurate models of physical systems.
Properties and Characteristics
The square root of 3 over 2, often represented as \( \frac{\sqrt{3}}{2} \), is an important mathematical constant with several interesting properties and characteristics:
- Irrational Number: \( \frac{\sqrt{3}}{2} \) is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-terminating and non-repeating.
- Approximate Value: The decimal approximation of \( \frac{\sqrt{3}}{2} \) is approximately 0.86602540378.
- Origin in Geometry: This constant appears in the context of the 30-60-90 triangle, where it represents the ratio of the length of the shorter leg (opposite the 30-degree angle) to the hypotenuse.
- Trigonometric Role: In trigonometry, \( \frac{\sqrt{3}}{2} \) is the cosine of a 30-degree angle or the sine of a 60-degree angle, denoted as \( \cos(30^\circ) \) or \( \sin(60^\circ) \).
- Graphical Representation: The value \( \frac{\sqrt{3}}{2} \) can be visualized on the unit circle, where it corresponds to specific coordinates representing angles of 30 degrees and 60 degrees.
- Relationship with Other Constants: This value frequently appears alongside other fundamental constants in various mathematical formulas, particularly in the context of trigonometric identities and geometric properties.
Overall, the square root of 3 over 2 is a significant constant in mathematics, playing crucial roles in geometry, trigonometry, and various applications across different fields.
Historical Context
The square root of 3 over 2, often denoted as , has a rich historical background deeply embedded in the development of mathematics across various ancient civilizations.
In Ancient Babylon, mathematical texts such as the Yale Babylonian Collection clay tablet (YBC 7289) from around 1800-1600 BCE, demonstrate advanced understanding of square roots and their approximations. The Babylonians used base 60 arithmetic to achieve impressive precision in their calculations.
Similarly, Ancient Egypt around 1650 BCE, as evidenced by the Rhind Mathematical Papyrus, showed knowledge of extracting square roots using an inverse proportion method. This text includes examples of practical applications and demonstrates the Egyptians' methodical approach to solving mathematical problems.
In Ancient India, significant contributions were made by mathematicians during the period of 800-500 BCE, with works like the Sulba Sutras detailing methods for finding precise approximations of square roots, including those of non-perfect squares. The Baudhayana Sulba Sutra, for instance, provides remarkably accurate values for square roots, demonstrating advanced understanding and techniques.
The Ancient Greeks also made substantial contributions to the understanding of irrational numbers, including the square root of 3 over 2. The work of mathematicians such as Theaetetus around 380 BCE formalized the concept that square roots of non-square integers are irrational. Euclid's Elements further codified these principles, which became foundational in the study of geometry and number theory.
Moving to the Medieval Period, European scholars continued to develop methods for calculating and representing square roots. For example, Regiomontanus (1436–1476) introduced a notation for square roots that influenced later mathematical texts.
Throughout these eras, the understanding and calculation of square roots evolved, paving the way for modern mathematical practices. The square root of 3 over 2, with its various applications and historical significance, remains a critical component of mathematical education and research.
Practical Examples and Problems
The square root of 3 over 2, often denoted as , is a significant value in mathematics with numerous practical applications. Below are several examples and problems demonstrating its use:
Example 1: Trigonometric Application
In trigonometry, appears as the sine and cosine of common angles. For instance:
Example 2: Geometry Problem
Consider an equilateral triangle with side length s. The height h of the triangle can be calculated as:
For s = 4 units, the height h is:
Hence, the height is approximately 3.464 units.
Problem 1: Evaluating an Expression
Simplify the expression:
Solution:
- Break down the expression:
- Simplify the expression:
Problem 2: Applying in Physics
In physics, the square root of 3 over 2 can be used to resolve vector components. Consider a force F = 10 N making an angle of 60° with the horizontal. The vertical component of the force is given by:
Thus, the vertical component is approximately 8.66 N.
Practice Problems
- Find the exact value of .
- Determine the height of an equilateral triangle with a side length of 10 units using .
- Simplify the expression .

Common Misconceptions
There are several common misconceptions regarding the square root of 3 over 2. Understanding these can help avoid mistakes and clarify misunderstandings in mathematical contexts.
-
Misconception 1: The Square Root of 3 Over 2 is Irrational but Expressed Incorrectly
Some people mistakenly simplify \(\sqrt{\frac{3}{2}}\) directly without considering its proper form. The correct approach is to rationalize the denominator:
- Multiply both numerator and denominator by \(\sqrt{2}\):
- Thus, \(\sqrt{\frac{3}{2}}\) simplifies to \(\frac{\sqrt{6}}{2}\), not just \(\sqrt{6}\).
\[\frac{\sqrt{3}}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{6}}{2}\]
-
Misconception 2: \(\sqrt{x^2}\) Equals \(\pm x\)
It is a common error to think that the square root of a squared number always yields both positive and negative roots. However, by definition, the square root function returns the non-negative root:
\(\sqrt{x^2} = |x|\), not \(\pm x\).
-
Misconception 3: Confusing Geometric Interpretations
In geometry, the expression \(\frac{\sqrt{3}}{2}\) is often associated with the height of an equilateral triangle with side length 1. Misinterpreting this can lead to errors in applying the concept in different geometric contexts, such as assuming it applies to other types of triangles without proper justification.
-
Misconception 4: Application in Trigonometry
In trigonometry, \(\frac{\sqrt{3}}{2}\) is often seen as the sine or cosine of 60 degrees or 30 degrees, respectively. Students might confuse these values when dealing with different angles, leading to incorrect calculations in trigonometric problems. For clarity:
- \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\)
- \(\cos(30^\circ) = \frac{\sqrt{3}}{2}\)
-
Misconception 5: Overlooking the Context of Radicals in Complex Numbers
When extending the concept of square roots to the complex plane, \(\sqrt{-1} = i\), some may incorrectly apply this to the square root of negative fractions, missing that \(\sqrt{-\frac{3}{2}}\) should be approached as \(\frac{\sqrt{3}}{2}i\).
Advanced Mathematical Context
The value of the square root of 3 over 2, denoted as \( \frac{\sqrt{3}}{2} \), plays a significant role in various advanced mathematical concepts. In this section, we explore its applications in different areas of mathematics.
Trigonometric Functions
In trigonometry, \( \frac{\sqrt{3}}{2} \) is commonly seen in the values of trigonometric functions for specific angles. For example:
- \(\sin(60^\circ) = \cos(30^\circ) = \frac{\sqrt{3}}{2}\)
- \(\sin(120^\circ) = \cos(150^\circ) = \frac{\sqrt{3}}{2}\)
These values are derived from the properties of a 30-60-90 triangle, where the ratio of the sides opposite the 30°, 60°, and 90° angles are 1, \( \sqrt{3} \), and 2, respectively.
Complex Numbers
When dealing with complex numbers, \( \frac{\sqrt{3}}{2} \) appears in the expression of roots of unity. For instance, the cube roots of unity are given by:
- \(1\)
- \( \frac{-1 + i\sqrt{3}}{2} \)
- \( \frac{-1 - i\sqrt{3}}{2} \)
These roots are crucial in solving polynomial equations and have applications in Fourier transforms and signal processing.
Geometry
In geometry, \( \frac{\sqrt{3}}{2} \) is used to calculate the height of an equilateral triangle. For an equilateral triangle with side length \( a \), the height \( h \) is given by:
\[
h = \frac{\sqrt{3}}{2}a
\]
This height is essential in determining the area of the triangle, which is calculated as:
\[
\text{Area} = \frac{\sqrt{3}}{4}a^2
\]
Vector Calculations
In vector mathematics, particularly in dot products and projections, the angle between vectors often involves trigonometric functions of \( \frac{\sqrt{3}}{2} \). For example, if two vectors form a 60° angle, the dot product incorporates \( \cos(60^\circ) = \frac{1}{2} \) and related trigonometric identities.
Calculus and Limits
The value \( \frac{\sqrt{3}}{2} \) appears in calculus, especially in the context of limits and series expansions. For instance, the limit involving trigonometric functions as angles approach specific values can utilize this constant for simplification. Consider the limit:
\[
\lim_{x \to 60^\circ} \frac{\sin(x) - \frac{\sqrt{3}}{2}}{x - 60^\circ} = \cos(60^\circ) = \frac{1}{2}
\]
Higher-Dimensional Spaces
In higher-dimensional spaces, \( \frac{\sqrt{3}}{2} \) is relevant in defining hyperplanes and multidimensional shapes. For example, in 3D space, the coordinates of points on a sphere or other surfaces can involve this value to express distances and relationships between points.
The square root of 3 over 2 is thus a fundamental value in advanced mathematical contexts, providing insights and solutions across various domains from trigonometry to higher-dimensional geometry.
Conclusion and Summary
The value of \(\frac{\sqrt{3}}{2}\) holds significant importance in various mathematical and scientific contexts. Throughout this comprehensive guide, we have explored its numerous applications and implications in fields such as trigonometry, geometry, and physics.
In trigonometry, \(\frac{\sqrt{3}}{2}\) frequently appears as a key value in the unit circle, particularly in the context of 30-degree and 60-degree angles. It represents the sine of 60 degrees and the cosine of 30 degrees, playing a crucial role in solving problems involving these angles.
Geometrically, this value is essential in the study of equilateral triangles and hexagons, contributing to the calculation of side lengths and heights. Its presence in these shapes underscores the interconnectedness of different branches of mathematics.
From a physical standpoint, \(\frac{\sqrt{3}}{2}\) appears in the analysis of forces, waves, and other phenomena where trigonometric functions are applied. Its precise value allows for accurate modeling and prediction in these scientific endeavors.
We have also discussed its properties, such as its irrationality and its representation as a decimal approximation, which is approximately 0.866. Understanding these properties enables a deeper appreciation of its mathematical significance.
In summary, the square root of 3 over 2 is a versatile and powerful value that bridges multiple areas of mathematics and science. Its applications are vast, ranging from theoretical constructs to practical problem-solving scenarios. By mastering the use of \(\frac{\sqrt{3}}{2}\), one gains a valuable tool for exploring and understanding the mathematical world.
As we conclude this guide, we encourage readers to continue exploring and applying this fundamental value in their studies and professional pursuits. The elegance and utility of \(\frac{\sqrt{3}}{2}\) will undoubtedly remain a cornerstone of mathematical and scientific inquiry.
Hướng dẫn cộng 2 căn 3 và căn 3 một cách dễ hiểu và chi tiết. Video phù hợp cho những ai đang học toán và muốn hiểu rõ hơn về cách tính toán với căn bậc hai.
2 căn(3) + căn(3) || Cách cộng 2 căn 3 và căn 3
READ MORE:
Video hướng dẫn cách tìm căn bậc hai của 3 một cách chi tiết và dễ hiểu, giúp bạn nắm vững khái niệm và áp dụng vào các bài toán thực tế.
Cách tìm căn bậc hai của 3













