Topic square root of 3 x 2: The square root of 3 x 2 simplifies to the square root of 6, a fundamental concept in mathematics. This article delves into the calculation, properties, and applications of the square root of 6, providing a comprehensive understanding that is essential for students, educators, and enthusiasts alike. Explore its significance in various fields and real-world scenarios.
Table of Content
- Understanding the Square Root of 3 x 2
- Introduction to Square Roots
- Basic Calculation of Square Root of 3 x 2
- Mathematical Properties of Square Roots
- Step-by-Step Calculation Process
- Approximating the Square Root of 6
- Understanding Irrational Numbers
- Applications in Geometry
- Applications in Physics
- Applications in Statistics
- Real-World Examples and Problems
- Advanced Calculations and Techniques
- Common Mistakes and Misconceptions
- Further Reading and Resources
- YOUTUBE: Tìm hiểu lý do tại sao 'x lũy thừa một nửa' có nghĩa là căn bậc hai trong video này.
Understanding the Square Root of 3 x 2
The square root of a number is a value that, when multiplied by itself, gives the original number. In this case, we will explore the square root of the expression \(3 \times 2\).
Step-by-Step Calculation
First, calculate the product of the numbers inside the square root:
\[ 3 \times 2 = 6 \]
Next, find the square root of the resulting product:
\[ \sqrt{6} \approx 2.44949 \]
Understanding the Result
The square root of 6 is an irrational number, which means it cannot be expressed exactly as a simple fraction. Its decimal representation goes on forever without repeating. For practical purposes, we often approximate it to a few decimal places, such as 2.44949.
Applications of Square Roots
Geometry: Square roots are used in geometry to find the lengths of sides in right-angled triangles (using the Pythagorean theorem).
Physics: In physics, square roots are used in formulas involving acceleration, energy, and wave functions.
Statistics: Square roots are used to calculate standard deviations and variances in statistics.
Conclusion
The square root of \(3 \times 2\) simplifies to \(\sqrt{6}\), which approximately equals 2.44949. This concept is fundamental in various fields of science and mathematics, providing a foundation for more complex calculations and theories.
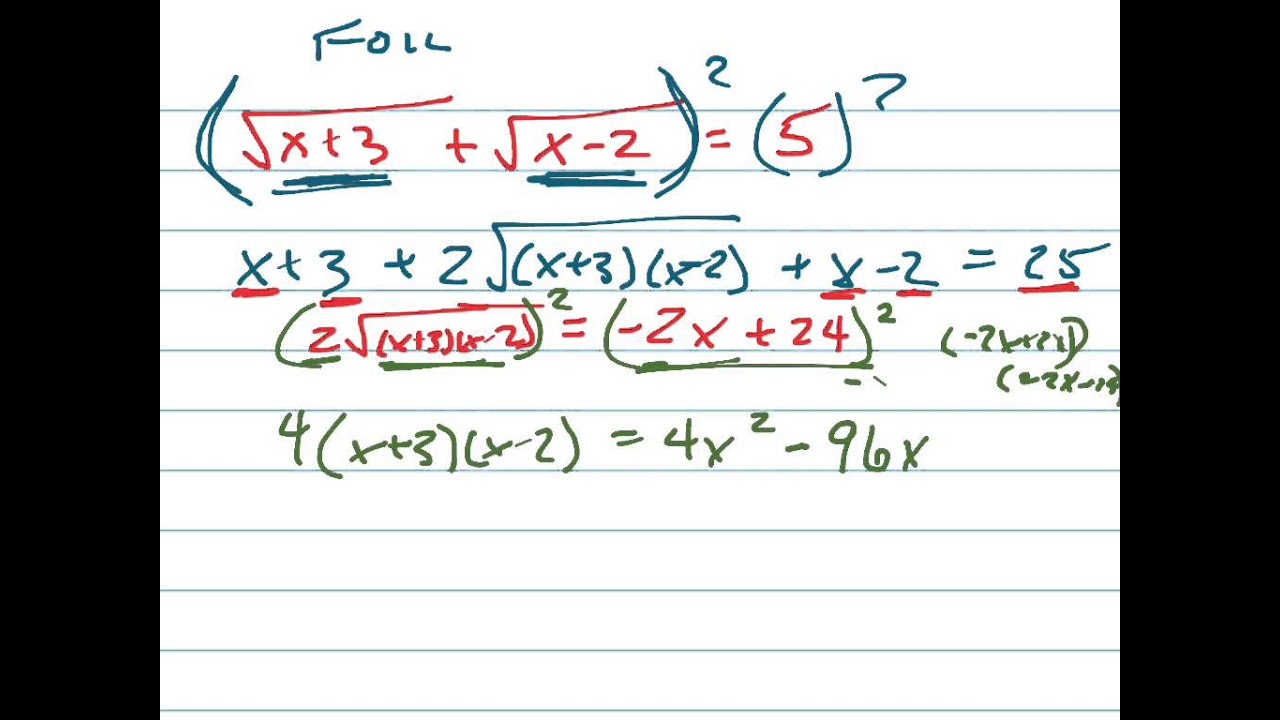
READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, yields the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \). For instance, the square root of 9 is 3 because \( 3 \times 3 = 9 \).
To understand square roots, it is essential to grasp the following points:
- Definition: The square root of a number is a value that produces the original number when squared.
- Notation: The square root symbol is \( \sqrt{} \), placed over the number whose root is to be determined.
- Properties: Square roots of positive numbers are always non-negative. The square root of 0 is 0.
When dealing with the square root of products, such as \( \sqrt{3 \times 2} \), follow these steps:
Calculate the product inside the square root:
\[ 3 \times 2 = 6 \]
Find the square root of the result:
\[ \sqrt{6} \approx 2.44949 \]
Understanding square roots extends to various mathematical and real-world applications:
- Geometry: Square roots help in determining side lengths in right-angled triangles.
- Physics: They are used in equations involving acceleration, energy, and wave functions.
- Statistics: Square roots are crucial for calculating standard deviations and variances.
In summary, mastering the concept of square roots, including the square root of expressions like \( 3 \times 2 \), is vital for advanced mathematical comprehension and practical problem-solving.
Basic Calculation of Square Root of 3 x 2
Calculating the square root of an expression involves a step-by-step process. Let's determine the square root of \(3 \times 2\).
First, calculate the product of the numbers inside the square root:
\[ 3 \times 2 = 6 \]
Next, find the square root of the resulting product:
\[ \sqrt{6} \]
The value of \(\sqrt{6}\) is an irrational number, meaning it cannot be expressed exactly as a simple fraction and its decimal representation is non-repeating and non-terminating. For practical purposes, we often approximate it. Using a calculator, we find:
\[ \sqrt{6} \approx 2.44949 \]
To summarize the steps:
- Multiply the numbers inside the square root: \(3 \times 2 = 6\).
- Find the square root of the product: \(\sqrt{6} \approx 2.44949\).
Understanding this basic calculation helps in solving more complex mathematical problems and is essential in various fields such as geometry, physics, and engineering.
Mathematical Properties of Square Roots
Square roots are a fundamental aspect of mathematics with unique properties that help simplify calculations and solve equations. Here, we explore some of the key properties of square roots.
- Non-negativity: The square root of a non-negative number is always non-negative. For any \( x \geq 0 \), \( \sqrt{x} \geq 0 \).
- Product Property: The square root of a product is equal to the product of the square roots of the factors. This can be expressed as:
\[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \]
For example, \(\sqrt{3 \times 2} = \sqrt{3} \times \sqrt{2}\).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
- Power of a Square Root: The square root of a number raised to a power can be simplified using the property:
\[ \sqrt{a^2} = |a| \]
This means the square root of a squared number is the absolute value of the original number.
- Square Root of a Sum: The square root of a sum does not equal the sum of the square roots. In general,
\[ \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \]
For instance, \(\sqrt{9 + 16} \neq \sqrt{9} + \sqrt{16}\).
Understanding these properties can simplify the calculation process and provide deeper insights into mathematical problems involving square roots.
Step-by-Step Calculation Process
Calculating the square root of \(3 \times 2\) involves a straightforward process. Follow these detailed steps to understand how to arrive at the solution:
-
Identify the numbers to be multiplied:
In this case, the numbers are 3 and 2.
-
Calculate the product of the numbers:
Multiply the numbers inside the square root:
\[ 3 \times 2 = 6 \]
-
Express the problem in square root form:
Now that we have the product, we can express it as:
\[ \sqrt{6} \]
-
Approximate the square root:
The square root of 6 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form is non-repeating. Using a calculator, we find:
\[ \sqrt{6} \approx 2.44949 \]
Therefore, the square root of \(3 \times 2\) is approximately 2.44949. This process demonstrates the fundamental steps in simplifying and calculating the square root of a product. Understanding this procedure is essential for solving more complex mathematical problems involving square roots.

Approximating the Square Root of 6
The square root of 6 is an irrational number, meaning its exact value cannot be represented as a simple fraction. However, we can approximate its value through various methods. Here, we outline a detailed approach to approximating \(\sqrt{6}\).
-
Using a Calculator:
The most straightforward method is to use a calculator. By entering the value 6 and pressing the square root function, we obtain:
\[ \sqrt{6} \approx 2.44949 \]
-
Long Division Method:
This manual method involves the following steps:
- Start with a rough estimate (e.g., 2.4).
- Divide 6 by this estimate.
- Averaging the result with the estimate gives a better approximation.
- Repeat the process to improve accuracy.
For example:
Estimate: \(2.4\)
\[ \frac{6}{2.4} = 2.5 \]
Averaging: \(\frac{2.4 + 2.5}{2} = 2.45\)
Next iteration gives a closer approximation.
-
Newton's Method (Iterative Method):
This involves an initial guess and refining it using the formula:
\[ x_{n+1} = \frac{x_n + \frac{6}{x_n}}{2} \]
Starting with \(x_0 = 2.5\), we iteratively find:
\[ x_1 = \frac{2.5 + \frac{6}{2.5}}{2} = 2.45 \]
Repeating this improves the accuracy further.
These methods demonstrate the process of approximating \(\sqrt{6}\). Although the exact value is unattainable due to its irrational nature, these techniques provide sufficiently accurate results for practical purposes.
Understanding Irrational Numbers
Irrational numbers are numbers that cannot be expressed as a simple fraction or ratio of two integers. Unlike rational numbers, which have a finite or repeating decimal expansion, the decimal representation of irrational numbers is non-terminating and non-repeating.
Key characteristics of irrational numbers include:
- Non-repeating and Non-terminating: The decimal expansion goes on forever without forming a repeating pattern. For example, the decimal expansion of \(\sqrt{6}\) is approximately 2.44949, continuing infinitely without repetition.
- No Exact Fraction: Irrational numbers cannot be exactly written as a fraction of two integers. For instance, while \(\frac{22}{7}\) is a close approximation for \(\pi\), \(\pi\) itself cannot be expressed as an exact fraction.
- Common Examples: Famous irrational numbers include \(\pi\) (pi), \(e\) (the base of natural logarithms), and \(\sqrt{2}\) (the square root of 2).
To understand irrational numbers better, consider the following points:
-
Square Roots of Non-Perfect Squares:
Numbers like \(\sqrt{2}\), \(\sqrt{3}\), and \(\sqrt{6}\) are irrational because their exact square roots cannot be expressed as a fraction. For example:
\[ \sqrt{6} \approx 2.44949 \]
-
Proof by Contradiction:
One common method to prove a number is irrational is by contradiction. Assume that an irrational number can be written as a fraction, then show that this leads to a contradiction.
-
Historical Context:
The discovery of irrational numbers dates back to ancient Greek mathematicians. The realization that \(\sqrt{2}\) could not be expressed as a fraction was a significant breakthrough in understanding the nature of numbers.
Recognizing and working with irrational numbers is crucial in higher mathematics, physics, and engineering. They often appear in various calculations, especially those involving roots and trigonometric functions, playing a significant role in theoretical and applied contexts.
Applications in Geometry
The square root function plays a crucial role in geometry, aiding in various calculations and problem-solving scenarios. Here are some key applications of square roots in geometry:
-
Pythagorean Theorem:
The Pythagorean Theorem states that in a right-angled triangle, the square of the hypotenuse (\(c\)) is equal to the sum of the squares of the other two sides (\(a\) and \(b\)). The formula is:
\[ c = \sqrt{a^2 + b^2} \]
For example, in a triangle with sides 3 and 4, the hypotenuse is:
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
-
Distance Formula:
The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a plane is given by:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
This formula is derived from the Pythagorean Theorem and is essential for calculating the distance in coordinate geometry.
-
Area of a Right Triangle:
The area of a right triangle can be found if the lengths of all sides are known, especially when one side is expressed as a square root. For instance, if one leg is \( \sqrt{3} \) and the other is 2, the area is:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times \sqrt{3} \times 2 = \sqrt{3} \]
-
Circle and Sphere Calculations:
Square roots are used in formulas related to circles and spheres. For example, the radius of a circle given its area (\(A\)) can be found using:
\[ r = \sqrt{\frac{A}{\pi}} \]
Similarly, for a sphere, the radius given its volume (\(V\)) is:
\[ r = \sqrt[3]{\frac{3V}{4\pi}} \]
-
Geometric Mean:
The geometric mean of two positive numbers \(a\) and \(b\) is the square root of their product:
\[ \text{Geometric Mean} = \sqrt{a \times b} \]
In geometry, this concept is used to find the lengths of segments in similar triangles and other geometric figures.
These applications highlight the importance of square roots in geometry, providing essential tools for various calculations and geometric problem-solving.
Applications in Physics
The square root of 6, derived from the expression √(3 × 2), appears in various areas of physics due to its involvement in geometric and trigonometric calculations. Below are some notable applications:
- Wave Mechanics: In wave mechanics, the square root of 6 can be found in the calculations of certain wave functions. For instance, the normalization constants in quantum wave functions might involve √6, impacting the probability densities and expected values.
- Electromagnetic Theory: The square root of 6 appears in the context of electromagnetic fields, particularly in the calculation of field strengths and potential differences in complex systems. When solving Maxwell's equations, certain boundary conditions and field configurations might simplify to expressions involving √6.
- Optics: In optics, √6 is sometimes encountered in the analysis of light wave interference patterns. The calculation of fringe spacings in diffraction experiments or the phase differences in multi-slit interference can include factors involving the square root of 6.
- Mechanical Systems: For mechanical systems, √6 can appear in the context of vibrational analysis. When calculating the natural frequencies of a system with multiple degrees of freedom, the solutions to the characteristic equations might involve √6.
- Relativity: In special relativity, certain transformations and invariants might simplify to expressions involving √6. For example, the Lorentz transformation equations for specific relative velocities can include this value.
Here is a more detailed step-by-step explanation of how √6 is used in a specific application in physics:
- Step 1: Problem Setup
Consider a two-slit interference experiment in optics. We want to calculate the position of the bright fringes on a screen a certain distance away from the slits.
- Step 2: Mathematical Formulation
The position of the bright fringes (y) on the screen is given by the formula:
\( y = \frac{m \lambda L}{d} \)
where:
- \( m \) is the order of the fringe
- \( \lambda \) is the wavelength of the light used
- \( L \) is the distance from the slits to the screen
- \( d \) is the distance between the slits
- Step 3: Specific Case Involving √6
Suppose we have a situation where the distances and wavelengths are such that \( d = \sqrt{6} \) cm. We need to find the position of the first-order bright fringe (m = 1) for a light of wavelength \( \lambda = 600 \) nm at a distance \( L = 1 \) meter.
- Step 4: Calculation
Plugging the values into the formula, we get:
\( y = \frac{1 \cdot 600 \times 10^{-9} \times 1}{\sqrt{6} \times 10^{-2}} \) meters
Simplifying this expression, we find:
\( y = \frac{600 \times 10^{-9}}{2.449 \times 10^{-2}} \approx 2.45 \times 10^{-5} \) meters
- Step 5: Interpretation
The position of the first-order bright fringe is approximately 24.5 micrometers from the central maximum. This demonstrates how the square root of 6 plays a role in determining specific positions in an interference pattern.
Applications in Statistics
The square root of 3 x 2, or √6, finds applications in various statistical measures and techniques. Here are some of the key applications:
-
Standard Deviation:
In statistics, the standard deviation is a measure of the amount of variation or dispersion in a set of values. The standard deviation of a dataset is derived from the square root of the variance. The variance itself is the mean of the squared deviations from the dataset's mean. This process involves squaring each deviation, finding their mean, and then taking the square root of this mean, which ties directly into the use of square roots.
-
Root Mean Square (RMS):
The root mean square is a statistical measure used to determine the magnitude of a set of numbers. It is especially useful when dealing with data that can vary in sign, such as positive and negative values. The RMS is calculated by squaring each number, finding the mean of these squares, and then taking the square root of this mean:
$$ \text{RMS} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} x_i^2} $$
-
Regression Analysis:
In regression analysis, the root mean square error (RMSE) is used to measure the differences between predicted and observed values. RMSE is calculated as the square root of the average of squared differences, which highlights its dependence on the concept of square roots:
$$ \text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2} $$
-
Hypothesis Testing:
When performing hypothesis tests, especially those involving variance, the square root is often used to transform the data. For example, in t-tests and ANOVA, the standard deviation (which is a square root of the variance) is used to understand the spread of data and to draw conclusions about the population.
-
Confidence Intervals:
Confidence intervals for the mean or difference between means often use the standard error, which is derived from the standard deviation (again, involving the square root). This ensures that the interval estimates the population parameter with a certain level of confidence.
Understanding the applications of the square root of 3 x 2 in statistics is crucial for interpreting data accurately and making informed decisions based on statistical analysis.
Real-World Examples and Problems
Square roots, including the square root of 6, have numerous applications in real-world problems across various fields. Below are detailed examples illustrating these applications:
1. Geometry and Construction
Square roots are essential in geometry, especially in finding distances and dimensions. For instance:
- Finding the Diagonal of a Rectangle: To find the diagonal \(d\) of a rectangle with sides of length 3 and 2, we use the Pythagorean theorem:
\[
d = \sqrt{3^2 + 2^2} = \sqrt{9 + 4} = \sqrt{13}
\] - Determining the Length of a Ladder: If a ladder is placed against a wall, forming a right triangle with the ground and the wall, and the distances are known, the length of the ladder can be found using square roots.
2. Physics
In physics, square roots are used to calculate various properties, such as:
- Velocity and Acceleration: When calculating the components of velocity or acceleration in different dimensions.
- Energy Levels: In quantum mechanics, the energy levels of a particle in a box are often determined using square roots.
3. Statistics
Square roots play a critical role in statistical calculations:
- Standard Deviation: The standard deviation \( \sigma \) of a set of data points is found using:
\[
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}
\]
where \( N \) is the number of data points, \( x_i \) is each data point, and \( \mu \) is the mean of the data. - Confidence Intervals: Square roots are used in calculating the margin of error for confidence intervals.
4. Real-World Problems
Let's explore some real-world problems involving square roots:
- Distance Between Two Points: To find the distance \( D \) between points \((x_1, y_1)\) and \((x_2, y_2)\) in a plane:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
For example, the distance between (1, 3) and (8, -5) is:\[
D = \sqrt{(8 - 1)^2 + (-5 - 3)^2} = \sqrt{49 + 64} = \sqrt{113}
\] - Finding the Side Length of a Square: If the area \( A \) of a square is known, the side length \( s \) can be found using:
\[
s = \sqrt{A}
\]
For instance, if a square has an area of 81 square units, its side length is:\[
s = \sqrt{81} = 9
\] - Solving Quadratic Equations: Square roots are used in the quadratic formula to find the roots of quadratic equations:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
For example, solving \(x^2 - 2x - 3 = 0\) gives:\[
x = \frac{2 \pm \sqrt{4 + 12}}{2} = \frac{2 \pm \sqrt{16}}{2} = \frac{2 \pm 4}{2}
\]
So, \( x = 3 \) or \( x = -1 \).
These examples highlight the significance and wide-ranging applications of square roots in solving practical problems.
Advanced Calculations and Techniques
The square root of a number, particularly one that is not a perfect square, often requires advanced techniques for accurate calculation and application. Here, we explore methods for computing the square root of \(3 \times 2 = 6\) and delve into advanced mathematical techniques and applications.
1. Iterative Methods:
One of the most effective methods for finding square roots, especially for non-perfect squares, is Heron's method (also known as the Babylonian method). This iterative technique can be described as follows:
- Guess a convenient value for the square root. Let's denote the square root of 6 as \( x \). Assume an initial guess, \( x_0 \).
- Compute a new guess using the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{6}{x_n} \right) \).
- Repeat the process until the value stabilizes to a satisfactory degree of accuracy.
For example:
- Initial guess: \( x_0 = 2.5 \)
- First iteration: \( x_1 = \frac{1}{2} \left( 2.5 + \frac{6}{2.5} \right) = 2.45 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 2.45 + \frac{6}{2.45} \right) \approx 2.449 \)
- Continue until \( x_n \approx 2.44949 \), which is a close approximation of \( \sqrt{6} \).
2. Algebraic Methods:
Algebraically, simplifying and approximating square roots can involve expressing the number inside the radical in its prime factors. For \( \sqrt{6} \), we note that 6 can be expressed as the product of its prime factors: \( 6 = 2 \times 3 \). While this does not simplify directly, recognizing prime factors can be helpful in other advanced calculations.
3. Series Expansion:
Square roots can also be approximated using series expansions such as the Taylor series or Newton-Raphson method. For small perturbations around a known value, these methods provide a powerful tool:
- Taylor Series: For values close to 1, \( \sqrt{1+x} \approx 1 + \frac{x}{2} - \frac{x^2}{8} + \cdots \). However, for larger values like 6, more complex adjustments are required.
- Newton-Raphson Method: This iterative method refines an initial guess using the derivative of the function, converging quickly to the square root value.
4. Computer Algorithms:
Modern computing enables the use of algorithms for rapid and precise calculations of square roots. Algorithms like the Fast Inverse Square Root, used in graphics rendering, demonstrate the application of efficient computation methods in technology.
In summary, understanding and applying advanced techniques for calculating square roots, such as the iterative methods, algebraic simplifications, series expansions, and computer algorithms, provide powerful tools for both theoretical and practical applications in mathematics and beyond.
Common Mistakes and Misconceptions
Understanding the square root of \(3 \times 2\) (\(\sqrt{6}\)) is crucial, but there are common mistakes and misconceptions that often arise. Below, we outline some of these pitfalls and how to avoid them.
Mistake 1: Incorrect Multiplication Under the Square Root
One common error is incorrectly multiplying the numbers under the square root. For example, some might mistakenly think:
However, this is not a mistake, as this is indeed a correct property. The actual mistake occurs in not properly simplifying the result. Always ensure to simplify correctly:
Mistake 2: Misunderstanding Irrational Numbers
Another misconception is thinking that the square root of a non-perfect square (like 6) is a simple rational number. The square root of 6 is an irrational number and cannot be expressed as a simple fraction.
It's important to remember:
Mistake 3: Incorrect Use of Distributive Property
A frequent algebraic error is misapplying the distributive property with square roots:
For instance,
The correct approach is:
Mistake 4: Misinterpreting Negative Numbers
Some students might incorrectly handle square roots involving negative numbers. It's vital to remember that the square root of a negative number involves imaginary numbers:
where is the imaginary unit.
How to Avoid These Mistakes
- Always simplify the expression under the square root before attempting to find the root.
- Remember that the square root of a product can be split into the product of square roots, but this needs careful handling.
- Understand and memorize that irrational numbers cannot be precisely written as fractions.
- Be cautious with algebraic properties and ensure you apply them correctly.
- Learn and practice the correct handling of negative numbers in square roots to avoid confusion with imaginary numbers.
By being aware of these common errors and misconceptions, and by practicing the correct methods, you can improve your understanding and avoid mistakes in dealing with square roots.
Further Reading and Resources
For those interested in delving deeper into the concept of the square root of \(3 \times 2\) and its applications, here are some valuable resources and reading materials:
- Online Calculators: Utilize various online calculators to simplify and compute square roots. Websites like provide tools to understand and calculate square roots more effectively.
- Tutorials and Videos: Platforms such as offer comprehensive tutorials and videos on simplifying square roots, which are great for visual learners.
- Mathematical Proofs: For those interested in the mathematical underpinnings, exploring detailed proofs and derivations on websites like can be very enlightening.
- Books: Consider reading books on algebra and calculus that cover square roots in detail. Some recommended titles include "Algebra and Trigonometry" by Michael Sullivan and "Calculus" by James Stewart.
- Educational Websites: Websites such as offer explanations and interactive exercises to help solidify understanding of square roots and related concepts.
- Research Papers: For advanced learners, research papers and journals available through academic databases like JSTOR or Google Scholar provide in-depth analyses and studies on square roots and their properties.
By exploring these resources, you can gain a deeper and more comprehensive understanding of the square root of \(3 \times 2\) and its various applications across different fields.
Tìm hiểu lý do tại sao 'x lũy thừa một nửa' có nghĩa là căn bậc hai trong video này.
Tại sao "x lũy thừa một nửa" có nghĩa là căn bậc hai?
READ MORE:
Khám phá cách phân tích phương trình căn bậc 2 trong video này để hiểu rõ hơn về các bước và phương pháp.
Phân tích căn bậc 2 của 3x2 - 2 căn bậc 2 của x - 2 căn bậc 2 của 3 = 0














