What's the Square Root of 3? Discover Its Importance and Applications

The square root of 3, denoted as \(\sqrt{3}\), is an irrational number. This means it cannot be expressed as a simple fraction, and its decimal representation goes on forever without repeating.

Decimal Representation

The approximate value of \(\sqrt{3}\) is:

\(\sqrt{3} \approx 1.7320508075688772\)

Mathematical Properties

• Square: \((\sqrt{3})^2 = 3\)
• Irrational number: It cannot be expressed as a ratio of two integers.
• Continued fraction representation: \(\sqrt{3} = 1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \cdots}}}\)

Geometric Interpretation

The square root of 3 can be visualized geometrically. For instance, in an equilateral triangle with side length 2, the height is \(\sqrt{3}\). This is derived from the Pythagorean theorem applied to the 30-60-90 right triangle formed by cutting the equilateral triangle in half:

height = \sqrt{2^2 - 1^2} = \sqrt{3}

Applications

The square root of 3 appears in various mathematical and scientific contexts, including:

1. Trigonometry: In trigonometric functions, particularly with angles of 30° and 60°.
2. Engineering: In calculations involving hexagonal structures and certain electrical circuits.
3. Geometry: In the properties of equilateral triangles and regular hexagons.

Approximations

While the exact value of \(\sqrt{3}\) is irrational, for practical purposes, it is often approximated as:

• 1.7321

The square root of 3, denoted as \( \sqrt{3} \), is an irrational number approximately equal to 1.732. It cannot be expressed as a simple fraction, and its decimal representation is non-repeating and non-terminating. The square root of 3 plays a significant role in various mathematical and scientific contexts, particularly in geometry and trigonometry.

Below are some key properties and facts about \( \sqrt{3} \):

• \( \sqrt{3} \) is an irrational number.
• The decimal approximation of \( \sqrt{3} \) is 1.73205080757...
• \( \sqrt{3} \) is often encountered in problems involving right-angled triangles, especially those with 30-60-90 degree angles.

Understanding \( \sqrt{3} \) involves exploring its occurrence in various mathematical constructs:

1. Geometry: In an equilateral triangle, the height can be found using \( \sqrt{3} \). If the side length of the triangle is \( a \), then the height is \( \frac{\sqrt{3}}{2}a \).
2. Trigonometry: The sine and cosine of 60 degrees are both related to \( \sqrt{3} \):
   • \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\)
   • \(\cos(30^\circ) = \frac{\sqrt{3}}{2}\)

The square root of 3 is essential in various calculations and practical applications:

• Engineering: Used in calculating forces in structures with triangular components.
• Physics: Appears in wave mechanics and other physical phenomena.

Understanding the square root of 3 enhances one's ability to solve complex mathematical problems and appreciate its significance in the real world.

The square root of 3, represented as \( \sqrt{3} \), is the positive real number that, when multiplied by itself, gives the number 3. Mathematically, this is expressed as:

\[ \sqrt{3} \times \sqrt{3} = 3 \]

\( \sqrt{3} \) is an irrational number, meaning it cannot be written as a simple fraction and its decimal representation is non-repeating and non-terminating. The approximate decimal value of \( \sqrt{3} \) is:

\[ \sqrt{3} \approx 1.73205080757... \]

The exact representation and properties of \( \sqrt{3} \) can be further explored through its presence in various mathematical contexts:

• Algebraic Properties:
  • \( \sqrt{3} \) is a solution to the equation \( x^2 = 3 \).
  • It can also be represented in exponential form as \( 3^{1/2} \).
• Geometric Properties:
  • In an equilateral triangle with side length \( a \), the height is \( \frac{\sqrt{3}}{2}a \).
  • In a 30-60-90 triangle, the ratio of the lengths of the sides opposite the 30° and 60° angles is \( \frac{1}{\sqrt{3}} \).

The square root of 3 also appears in trigonometric functions:

• \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\)
• \(\cos(30^\circ) = \frac{\sqrt{3}}{2}\)

Understanding the mathematical definition of \( \sqrt{3} \) is fundamental to appreciating its role in various branches of mathematics and its practical applications in science and engineering.

The concept of square roots, including the square root of 3, has ancient origins, tracing back to the early mathematicians of Babylonian and Greek civilizations. These ancient scholars laid the groundwork for our understanding of irrational numbers.

One of the earliest known methods for approximating square roots was developed by the Babylonians around 2000 BCE. They used a form of iterative algorithm similar to the modern-day Newton-Raphson method to find approximate values of square roots, including \( \sqrt{3} \).

In ancient Greece, the Pythagoreans were among the first to recognize the existence of irrational numbers. They discovered that certain lengths, such as the diagonal of a unit square, could not be expressed as a ratio of two integers. This discovery was revolutionary and led to the broader exploration of irrational numbers, including \( \sqrt{3} \).

During the Hellenistic period, Euclid's Elements provided a systematic approach to geometry, which included the properties of square roots. Although Euclid did not specifically address \( \sqrt{3} \), his work laid the foundational principles that facilitated further investigations into irrational numbers.

In the Middle Ages, Islamic mathematicians made significant advancements in algebra and number theory. Al-Khwarizmi, a prominent mathematician, wrote extensive texts that included methods for solving quadratic equations, thereby contributing to the understanding of square roots.

By the Renaissance, European mathematicians such as Fibonacci and Cardano further refined methods for calculating square roots and recognizing their significance in various mathematical contexts. The development of algebraic notation by Descartes and others provided a more systematic way to represent and work with irrational numbers like \( \sqrt{3} \).

The formal proof of the irrationality of \( \sqrt{3} \) came much later, building on the work of these earlier mathematicians. The understanding and calculation of \( \sqrt{3} \) continued to evolve with the advancement of mathematical theory and computational techniques.

Today, \( \sqrt{3} \) is a well-established mathematical constant, integral to various fields such as geometry, trigonometry, and calculus. Its historical journey from ancient approximations to modern applications reflects the enduring quest for mathematical knowledge and precision.

The square root of 3, denoted as \( \sqrt{3} \), is an important mathematical constant with several intriguing properties. Understanding these properties can enhance your comprehension of its applications in various mathematical fields.

• Irrational Number: \( \sqrt{3} \) is an irrational number, meaning it cannot be expressed as a simple fraction of two integers. Its decimal representation is non-repeating and non-terminating:

  \[ \sqrt{3} \approx 1.73205080757... \]

• Algebraic Property: The square root of 3 satisfies the equation:

  \[ (\sqrt{3})^2 = 3 \]

• Exponential Form: \( \sqrt{3} \) can be expressed in exponential form as:

  \[ 3^{1/2} \]

• Geometric Significance: In geometry, \( \sqrt{3} \) often appears in the context of right triangles and equilateral triangles:
  • For an equilateral triangle with side length \( a \), the height (h) is given by:

    \[ h = \frac{\sqrt{3}}{2}a \]

  • In a 30-60-90 triangle, the ratio of the sides is:

    \[ 1 : \sqrt{3} : 2 \]

• Trigonometric Values: The square root of 3 is fundamental in trigonometry, particularly with angles of 30° and 60°:
  • \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\)
  • \(\cos(30^\circ) = \frac{\sqrt{3}}{2}\)
  • \(\tan(60^\circ) = \sqrt{3}\)
• Relationship with Other Irrational Numbers: \( \sqrt{3} \) is related to other irrational numbers such as \( \sqrt{2} \) and \( \sqrt{5} \). For example, it can be used to express certain algebraic identities:

  \[ \sqrt{3} \cdot \sqrt{3} = 3 \]

These properties make \( \sqrt{3} \) a versatile and essential element in various mathematical problems and applications, from basic geometry to advanced trigonometric calculations.

The square root of 3, represented as \( \sqrt{3} \), has both an exact form and several approximate values that are commonly used in calculations. Understanding these values is essential for various mathematical applications.

Exact Value:

The exact value of the square root of 3 is simply \( \sqrt{3} \). This value is irrational, meaning it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion.

Approximate Decimal Value:

The approximate value of \( \sqrt{3} \) to several decimal places is:

\[ \sqrt{3} \approx 1.73205080757... \]

For practical purposes, this value is often rounded to a few decimal places:

• To 2 decimal places: 1.73
• To 3 decimal places: 1.732
• To 4 decimal places: 1.7321

Fractional Approximations:

While \( \sqrt{3} \) is irrational, it can be approximated by rational numbers for simpler calculations. Some common fractional approximations include:

• \(\frac{97}{56} \approx 1.7321\)
• \(\frac{577}{333} \approx 1.7320\)

Continued Fraction Representation:

The continued fraction representation of \( \sqrt{3} \) provides a way to express it as an infinite series of fractions, which can give increasingly accurate approximations:

\[ \sqrt{3} = 1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \cdots}}} \]

Comparison with Other Square Roots:

For context, it is helpful to compare \( \sqrt{3} \) with other common square roots:

• \(\sqrt{2} \approx 1.414\)
• \(\sqrt{5} \approx 2.236\)

These comparisons illustrate the relative size of \( \sqrt{3} \) and help in understanding its magnitude.

Knowing both the exact and approximate values of \( \sqrt{3} \) is crucial for precise mathematical calculations and for simplifying complex problems where an exact value may not be necessary.

The square root of 3, \( \sqrt{3} \), plays a significant role in various geometric contexts. Its unique properties make it essential in understanding the dimensions and relationships within different geometric shapes and figures.

Equilateral Triangle:

In an equilateral triangle, all sides are of equal length, and all internal angles are 60 degrees. The height (\(h\)) of an equilateral triangle with side length (\(a\)) can be determined using \( \sqrt{3} \):

\[ h = \frac{\sqrt{3}}{2}a \]

This relationship is derived from splitting the equilateral triangle into two 30-60-90 right triangles, where the height corresponds to the longer leg of these right triangles.

30-60-90 Triangle:

The 30-60-90 triangle is a special type of right triangle with angles of 30 degrees, 60 degrees, and 90 degrees. The side lengths of a 30-60-90 triangle maintain a specific ratio, which involves \( \sqrt{3} \):

• The side opposite the 30° angle (shorter leg) is \( x \).
• The side opposite the 60° angle (longer leg) is \( x\sqrt{3} \).
• The hypotenuse (opposite the 90° angle) is \( 2x \).

These ratios make it easy to determine the lengths of the sides if one side length is known.

Area of a Regular Hexagon:

A regular hexagon can be divided into six equilateral triangles. Given the side length (\(a\)) of the hexagon, the area (\(A\)) can be calculated using \( \sqrt{3} \):

\[ A = \frac{3\sqrt{3}}{2}a^2 \]

This formula highlights the importance of \( \sqrt{3} \) in finding the area of regular hexagons, which are common in various geometric and real-world applications.

Cube Diagonal:

In three-dimensional geometry, \( \sqrt{3} \) appears in the context of the space diagonal of a cube. For a cube with side length (\(a\)), the length of the space diagonal (\(d\)) is given by:

\[ d = a\sqrt{3} \]

This is derived from the Pythagorean theorem applied in three dimensions.

The square root of 3 is also relevant in various other geometric constructs and problems, including trigonometric calculations and the properties of polygons. Understanding its role in geometry can significantly enhance problem-solving skills and the comprehension of spatial relationships.

The square root of 3, \( \sqrt{3} \), is not just a mathematical curiosity; it has numerous practical applications in various fields. Here are some of the real-life applications where \( \sqrt{3} \) plays a crucial role:

• Engineering and Architecture:

  In engineering and architectural design, the square root of 3 is often used in calculations involving triangular supports and structures. For example, in the design of trusses and bridges, the properties of 30-60-90 triangles, which incorporate \( \sqrt{3} \), are used to ensure stability and strength.

• Electrical Engineering:

  In electrical engineering, the square root of 3 appears in the analysis of three-phase electrical power systems. The line-to-line voltage in a balanced three-phase system is \( \sqrt{3} \) times the line-to-neutral voltage, which is essential for efficient power distribution and transmission.

  \[ V_{line-to-line} = \sqrt{3} \times V_{line-to-neutral} \]

• Physics:

  In physics, \( \sqrt{3} \) is used in various formulas and calculations. For instance, in wave mechanics, the speed of waves in certain mediums can involve factors of \( \sqrt{3} \). Additionally, the analysis of forces in static equilibrium problems often employs geometric relationships involving \( \sqrt{3} \).

• Mathematics and Trigonometry:

  The square root of 3 is fundamental in trigonometry, particularly in the calculation of angles and side lengths in special triangles. These principles are applied in fields ranging from computer graphics to astronomy, where precise measurements are crucial.

• Construction:

  In construction, the use of equilateral triangles and hexagons, which involve \( \sqrt{3} \), is common for creating stable and efficient structures. For example, the design of roof trusses often incorporates triangular shapes to evenly distribute weight and provide robust support.

• Crystallography:

  In crystallography, the arrangement of atoms in certain crystal structures involves geometric configurations that include \( \sqrt{3} \). Understanding these configurations helps in the study of material properties and the development of new materials.

These applications highlight the versatility and importance of \( \sqrt{3} \) in solving practical problems and advancing technology in various fields. Its presence in engineering, physics, construction, and beyond underscores the value of this mathematical constant in everyday life.

The square root of 3, \( \sqrt{3} \), finds significant applications across multiple fields, each leveraging its unique properties for various practical and theoretical purposes. Here are some of the key areas where \( \sqrt{3} \) is utilized:

• Engineering:

  In mechanical and civil engineering, \( \sqrt{3} \) is essential in the design and analysis of triangular frameworks and trusses. The stability and load distribution in these structures often depend on geometric relationships involving \( \sqrt{3} \).

• Electrical Engineering:

  Three-phase power systems, which are common in industrial and commercial power distribution, use \( \sqrt{3} \) to relate line-to-line and line-to-neutral voltages. This relationship is crucial for the efficient transmission of electrical power.

  \[ V_{line-to-line} = \sqrt{3} \times V_{line-to-neutral} \]

• Physics:

  In physics, \( \sqrt{3} \) appears in various contexts, such as the analysis of wave mechanics and static equilibrium. For example, it is used to calculate the resultant forces in systems involving triangular components.

• Mathematics:

  In mathematics, \( \sqrt{3} \) is fundamental in trigonometry and geometry. It helps solve problems involving special triangles, such as 30-60-90 triangles, and appears in formulas for calculating distances and angles.

• Architecture:

  Architects use \( \sqrt{3} \) in the design of structures that incorporate equilateral triangles and hexagons. These shapes are not only aesthetically pleasing but also provide structural integrity and efficiency.

• Crystallography:

  In crystallography, \( \sqrt{3} \) helps describe the geometric arrangement of atoms in crystal lattices. Understanding these arrangements is vital for studying material properties and developing new materials.

• Computer Graphics:

  In computer graphics, \( \sqrt{3} \) is used in algorithms that generate and manipulate geometric shapes and patterns. This includes rendering techniques for creating realistic visual representations of objects.

• Astronomy:

  Astronomers use \( \sqrt{3} \) in calculations involving the triangulation of distances to celestial objects. This helps in accurately determining their positions and movements.

Overall, \( \sqrt{3} \) is a versatile mathematical constant that is deeply embedded in the methodologies and solutions across various disciplines. Its wide-ranging applications underscore its importance in both theoretical and practical contexts.

The square root of 3, denoted as √3, is an irrational number that cannot be expressed as a simple fraction. Its approximate value is 1.7320508075688772. To calculate the square root of 3, we can use several methods, including the long division method and the Newton-Raphson method.

Long Division Method

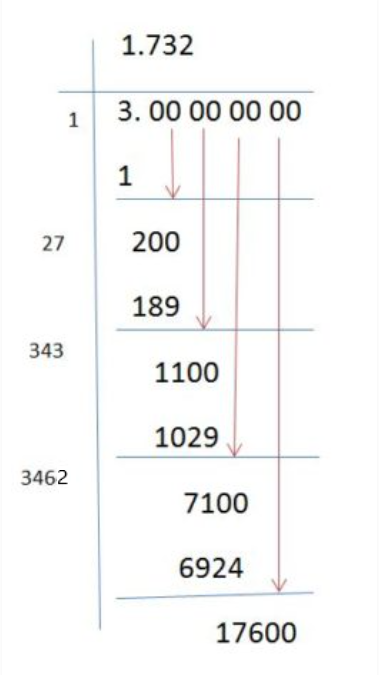
The long division method is a manual technique to find the square root of a number. Here are the steps to calculate the square root of 3 using this method:

1. Step 1: Write the number 3 as 3.000000000000 (to ensure accuracy, extend the number with as many zeros as needed).
2. Step 2: Group the digits in pairs, starting from the decimal point and moving both left and right. In this case, 3.00 becomes 3. 00 00 00 ...
3. Step 3: Find the largest number whose square is less than or equal to 3. The number is 1, because 1 × 1 = 1. Place this as the first digit of the quotient.
4. Step 4: Subtract 1 from 3, leaving a remainder of 2. Bring down the next pair of zeros, making it 200.
5. Step 5: Double the quotient (which is 1) to get 2. Determine how many times 20 can go into 200 without exceeding it. The number is 7, because 27 × 7 = 189.
6. Step 6: Place 7 in the quotient, making it 1.7. Subtract 189 from 200 to get 11. Bring down the next pair of zeros to get 1100.
7. Step 7: Double the quotient (which is now 17) to get 34. Determine how many times 340 can go into 1100 without exceeding it. The number is 3, because 343 × 3 = 1029.
8. Step 8: Place 3 in the quotient, making it 1.73. Subtract 1029 from 1100 to get 71. Continue this process to get more decimal places as needed.

Newton-Raphson Method

This method provides an iterative approach to finding the square root. Here’s how it works:

1. Step 1: Start with an initial guess, let's say x₀ = 1.5.
2. Step 2: Use the formula x₁ = (x₀ + 3 / x₀) / 2 to find the next approximation.
3. Step 3: Repeat the process with x₁ to find x₂, and so on, until the difference between successive approximations is less than a desired tolerance level.

After several iterations, you will get an approximation of √3.

Using Calculators and Software

For a quick and accurate result, you can use calculators or mathematical software. Most scientific calculators have a square root function that can provide √3 to many decimal places. Online tools and software like WolframAlpha, Python, and MATLAB can also be used to calculate square roots with high precision.

The square root of 3 is essential in various mathematical applications, including geometry and trigonometry. Its accurate calculation is crucial for precise measurements and computations in these fields.

There are several methods to manually calculate the square root of 3. Here, we will explore two primary methods: the estimation method and the long division method.

Estimation Method

The estimation method is a simple way to approximate the value of the square root of 3:

1. Start with numbers you know: You know that \(1^2 = 1\) and \(2^2 = 4\). Since 3 is between 1 and 4, \(\sqrt{3}\) must be between 1 and 2.
2. Make a guess: Guess a number between 1 and 2 that might square to close to 3. A good starting guess is 1.5 because it’s halfway between.
3. Adjust your guess: Since \(1.5^2 = 2.25\), which is less than 3, you need a bigger number. Try 1.7 next, because \(1.7^2 = 2.89\), which is closer to 3.
4. Fine-tune your guess: If you want to be more precise, you can try numbers closer to 1.7, like 1.73 or 1.74, and see which gets closer to 3 when squared. \(1.73^2 = 2.9929\), very close to 3.

Long Division Method

The long division method provides a more precise way to calculate the square root of 3:

1. Write 3 as 3.000000, grouping the zeros after the decimal point in pairs.
2. Think of a number which, when multiplied by itself, is less than or equal to 3. This number is 1.
3. Divide 3 by 1 to get a quotient of 1 and a remainder of 2.
4. Drag a pair of zeros down next to the remainder, making it 200.
5. Double the divisor (1) to get 2, and find a digit \(X\) such that \(2X \times X \leq 200\). The digit is 7 (since \(27 \times 7 = 189\)).
6. Update the quotient by adding 7 after the decimal point, and update the divisor to 27 + 7 = 34.
7. Repeat the process: Continue bringing down pairs of zeros and finding new digits for the quotient, adjusting the divisor accordingly to achieve greater precision.

Using these methods, you can manually calculate the square root of 3 to a desired degree of accuracy. The approximate value of \(\sqrt{3}\) is 1.73205080757.

Calculating the square root of 3 using calculators and software is a straightforward process. Modern tools provide both exact and approximate values quickly and efficiently. Here's a step-by-step guide on how to use various calculators and software to find the square root of 3:

Using Online Calculators

There are several online calculators available that can compute the square root of 3. Some popular options include:

Here’s how to use these calculators:

1. Navigate to the website of the calculator.
2. Enter the number 3 in the input field designated for the radicand.
3. Click the button to calculate the square root. The result will be displayed immediately.

Using Calculator Apps

Several mobile apps also offer square root calculation features. Popular choices include:

To use these apps:

1. Download and install the app on your mobile device.
2. Open the app and select the square root calculator function.
3. Input the number 3 and press the calculate button.

Using Scientific Calculators

Most scientific calculators, whether physical devices or software-based, include a square root function. Follow these steps:

1. Turn on the calculator and ensure it is set to standard mode (not in scientific notation).
2. Press the square root button (√), usually located on the calculator's front panel.
3. Enter the number 3 and press the equals button (=) to get the result.

Using Spreadsheet Software

Spreadsheet applications like Microsoft Excel, Google Sheets, and Apple Numbers can also calculate the square root of 3:

1. Open a new spreadsheet in your preferred software.
2. Click on a cell where you want the result to appear.
3. Type the formula =SQRT(3) and press Enter. The cell will display the square root of 3.

Using Programming Languages

If you are familiar with programming, many languages offer built-in functions to calculate square roots. Here are a few examples:

• Python: import math; math.sqrt(3)
• JavaScript: Math.sqrt(3)
• R: sqrt(3)

Using these methods, you can easily and accurately find the square root of 3 for any application.

The square root of 3 frequently appears in trigonometry, particularly in relation to certain standard angles and the values of trigonometric functions. Here are some notable instances:

• 30° and 60° Angles: In a 30°-60°-90° triangle, the sides are in the ratio 1:√3:2. The side opposite the 60° angle has a length of √3. This gives rise to the following trigonometric values:

  • $\backslash sin\; 60^\backslash circ\; =\; \backslash cos\; 30^\backslash circ\; =\; \backslash frac\{\backslash sqrt\{3\}\}\{2\}$
  • $\backslash tan\; 60^\backslash circ\; =\; \backslash cot\; 30^\backslash circ\; =\; \backslash sqrt\{3\}$
  • $\backslash csc\; 60^\backslash circ\; =\; \backslash sec\; 30^\backslash circ\; =\; \backslash frac\{2\}\{\backslash sqrt\{3\}\}$

• Inverse Trigonometric Functions: The square root of 3 also appears in the inverse trigonometric functions. For instance, if we need to solve for an angle x where $\backslash csc(x)\; =\; \backslash sqrt\{3\}$, we get:

  $\backslash csc(x)\; =\; \backslash sqrt\{3\}\; \backslash implies\; \backslash sin(x)\; =\; \backslash frac\{1\}\{\backslash sqrt\{3\}\}\; \backslash implies\; x\; =\; 30^\backslash circ\; \backslash text\{\; or\; \}\; 150^\backslash circ$

• Trigonometric Identities: In the Pythagorean identity, $\backslash sin^2(x)\; +\; \backslash cos^2(x)\; =\; 1$, for $x\; =\; 60^\backslash circ$, we see:

  $\backslash left(\; \backslash frac\{\backslash sqrt\{3\}\}\{2\}\; \backslash right)^2\; +\; \backslash left(\; \backslash frac\{1\}\{2\}\; \backslash right)^2\; =\; \backslash frac\{3\}\{4\}\; +\; \backslash frac\{1\}\{4\}\; =\; 1$

The presence of √3 in these values is essential for solving various trigonometric equations and understanding the relationships within right triangles and the unit circle.

The square root of 3, denoted as \(\sqrt{3}\), holds significant importance in various mathematical and scientific fields. Its value is approximately 1.732, and it plays a crucial role in numerous applications and theories.

Here are some key areas where \(\sqrt{3}\) is particularly important:

• Geometry:

  The square root of 3 is fundamental in geometry, especially in calculations involving equilateral triangles. The height of an equilateral triangle with side length \(a\) is given by \(\frac{\sqrt{3}}{2}a\), and the area is \(\frac{\sqrt{3}}{4}a^2\). This makes \(\sqrt{3}\) essential for understanding and working with these shapes.

• Trigonometry:

  In trigonometry, \(\sqrt{3}\) appears in the tangent and sine of 60 degrees (\(\pi/3\) radians). Specifically, \(\tan(60^\circ) = \sqrt{3}\) and \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\). These relationships are critical in solving problems involving angles and lengths in right triangles.

• Physics:

  In physics, \(\sqrt{3}\) is encountered in various contexts, such as in wave equations and crystallography. For instance, in the study of hexagonal crystal structures, the ratio of the lattice constants involves \(\sqrt{3}\), influencing the properties and behavior of materials.

• Engineering:

  Engineers frequently use \(\sqrt{3}\) in calculations related to power systems, especially in three-phase electrical systems. The line-to-line voltage in a balanced three-phase system is \(\sqrt{3}\) times the line-to-neutral voltage, which is crucial for designing and analyzing these systems.

• Mathematics:

  Mathematically, \(\sqrt{3}\) is an irrational number, meaning it cannot be expressed as a simple fraction. This property makes it an interesting subject of study in number theory. Additionally, its irrational nature has implications for various mathematical proofs and theories.

The presence of \(\sqrt{3}\) in these diverse fields underscores its wide-ranging importance and the interconnectedness of mathematical concepts across different scientific disciplines.

There are several misconceptions regarding the square root of 3. Here, we clarify some of the most common ones:

• Misconception: The square root of 3 is a rational number.

  Clarification: The square root of 3 (\(\sqrt{3}\)) is an irrational number. This means it cannot be expressed as a simple fraction of two integers. Its decimal representation is non-terminating and non-repeating, approximately equal to 1.73205080757...

• Misconception: The square root of 3 can be exactly calculated.

  Clarification: While we can approximate \(\sqrt{3}\) to many decimal places using various methods, its exact value is irrational and cannot be exactly calculated. For practical purposes, it is often approximated to a certain number of decimal places.

• Misconception: The square root of 3 is the same as the cube root of 3.

  Clarification: The square root of 3 and the cube root of 3 are different. The square root of 3 is approximately 1.732, while the cube root of 3 is approximately 1.442. They represent different mathematical operations and are not equivalent.

• Misconception: Trigonometric values involving \(\sqrt{3}\) can be simplified to exact fractions.

  Clarification: Trigonometric values like \(\tan(60^\circ) = \sqrt{3}\) and \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\) involve the square root of 3 and cannot be further simplified to exact fractions without \(\sqrt{3}\).

The square root of 3 is an important mathematical constant that can be represented in various number systems. Here is a detailed look at how it appears in different systems:

Decimal System

In the decimal system, the square root of 3 is an irrational number. It cannot be expressed as an exact fraction, and its decimal representation is non-terminating and non-repeating. The approximate value is:

\(\sqrt{3} \approx 1.7320508075688772\)

Fractional Approximations

While the exact value cannot be expressed as a fraction, we can use fractional approximations to estimate it. Common approximations include:

• \(\frac{265}{153} \approx 1.7320261\)
• \(\frac{1351}{780} \approx 1.7320513\)

Binary System

In the binary system, the square root of 3 is also represented as a non-terminating, non-repeating sequence. Its binary representation starts as follows:

\(\sqrt{3} \approx 1.1011101101100110...\) (binary)

Hexadecimal System

In the hexadecimal system, the square root of 3 is expressed similarly to the decimal system but in base 16. The initial digits are:

\(\sqrt{3} \approx 1.BB67AE8584CAA73B...\) (hexadecimal)

Historical Number Systems

Historically, different cultures had unique ways of representing irrational numbers like \(\sqrt{3}\). For example:

• Babylonian System: The Babylonians used a base-60 (sexagesimal) system, where they would approximate \(\sqrt{3}\) using values close to its true value.
• Egyptian System: Ancient Egyptians used unit fractions to approximate irrational numbers, though their methods for \(\sqrt{3}\) are not as well-documented as for other constants like \(\sqrt{2}\).

Understanding the representation of \(\sqrt{3}\) in different number systems helps in various applications, from computer science to historical mathematics, providing a bridge between modern and ancient numerical methods.

The visual representation of the square root of 3 can be highly beneficial in understanding its properties and implications in mathematics. Here are some ways to visualize this irrational number:

• Number Line Representation:

  Place the square root of 3 on a number line to see its position relative to whole numbers and other square roots. This helps in understanding its approximate value of 1.732.

• Geometric Representation:

  In geometry, a common method to visualize the square root of 3 is by constructing an equilateral triangle. Each side of the triangle has a length of 2, and the height of this triangle will be the square root of 3.

  Equilateral Triangle: Draw an equilateral triangle with each side of length 2 units. The altitude of this triangle, which divides it into two 30-60-90 right triangles, will be $$ 3 2 √ 3 . 30-60-90 Triangle: In this right triangle, the ratio of the sides is 1:√3:2. Thus, if the shorter leg is 1, the longer leg (which corresponds to the height of the equilateral triangle) is √3.

• Graphical Tools:

  Using tools like Desmos, you can create dynamic visualizations that allow you to see and manipulate the square root of 3 in various contexts, such as plotting it on a graph or using it in interactive geometric constructions.

These visualizations provide a deeper understanding of the square root of 3, making it easier to grasp its significance and application in various mathematical contexts.

• What is the square root of 3?

  The square root of 3 is approximately 1.732. It is an irrational number, meaning it cannot be exactly represented as a simple fraction.

• How is the square root of 3 used in mathematics?

  The square root of 3 is used in various mathematical contexts, including geometry, algebra, and trigonometry. It often appears in problems involving right triangles, where it is part of the solution to the Pythagorean theorem.

• Can the square root of 3 be simplified?

  No, the square root of 3 cannot be simplified into a simpler radical form as it is already in its simplest radical form.

• What is an example of the square root of 3 in geometry?

  In an equilateral triangle, the height can be found using the square root of 3. If each side of the triangle is 2 units, the height will be \( \sqrt{3} \) units, derived from the Pythagorean theorem.

• Why is the square root of 3 important in trigonometry?

  In trigonometry, the square root of 3 is significant in the calculation of certain trigonometric functions, such as the tangent of 60 degrees, which equals \( \sqrt{3} \).

• How do calculators find the square root of 3?

  Modern calculators use iterative algorithms such as the Newton-Raphson method to compute the square roots of numbers, including 3, with high precision.

• What are some practical applications of the square root of 3?

  Practical applications of the square root of 3 include engineering, physics, and computer science, particularly in solving problems involving roots and exponents, wave functions, and other calculations requiring precise numerical values.

The square root of 3, approximately 1.732, plays a significant role in various mathematical and scientific fields. Understanding this irrational number provides insights into more complex mathematical concepts and real-world applications.

• Mathematical Significance: The square root of 3 is essential in geometry, especially in the study of equilateral triangles and the Pythagorean theorem. It is also pivotal in trigonometry, appearing in the values of sine and cosine for 30° and 60° angles.
• Scientific Applications: This constant is used in various scientific calculations, including physics and engineering, where precise measurements and ratios are crucial.
• Educational Importance: Learning about the square root of 3 helps students grasp the concept of irrational numbers and their properties, fostering a deeper understanding of number theory and algebra.
• Technological Utilization: In modern technology, algorithms and software often utilize the square root of 3 for simulations, optimizations, and problem-solving in fields like computer graphics and numerical analysis.

In summary, the square root of 3 is not just a mathematical curiosity but a fundamental component of many theoretical and practical disciplines. Its understanding enriches our comprehension of mathematics and its applications in the world around us.