Topic square root of 340: Unlock the secrets of the square root of 340 with our comprehensive guide. From mathematical calculations to real-life applications, this article will help you understand and appreciate the importance of this fascinating number. Dive in and explore the world of square roots, prime factorization, and more.
Table of Content
- Square Root of 340
- Introduction
- Definition and Properties
- Approximation Methods
- Prime Factorization
- Irrational Number Explanation
- Real-life Applications
- Step-by-step Calculation
- Using a Calculator
- Square Root Simplification
- Comparing with Other Square Roots
- Historical Context
- Common Mistakes
- FAQs
- Conclusion
- YOUTUBE:
Square Root of 340
The square root of 340 is represented mathematically as:
\(\sqrt{340}\)
Calculating the square root of 340, we get an approximate value:
\(\sqrt{340} \approx 18.43908891\)
Properties of the Square Root of 340
- The square root of 340 is an irrational number, which means it cannot be expressed as a simple fraction.
- The square root of 340 lies between the integers 18 and 19.
- The exact value of the square root of 340 is an infinite non-repeating decimal.
Applications
The square root of 340 can be used in various fields, such as:
- Engineering
- Physics
- Architecture
Mathematical Calculation
To calculate the square root of 340 using a calculator:
- Enter the number 340.
- Press the square root (√) button.
- The calculator will display the result: approximately 18.43908891.
| Number | Square Root |
| 340 | \(\sqrt{340} \approx 18.43908891\) |

READ MORE:
Introduction
The square root of 340 is a mathematical concept that holds significant importance in various fields. Represented as \(\sqrt{340}\), this value is an irrational number, meaning it cannot be expressed as a simple fraction. The approximate value of the square root of 340 is 18.439, and understanding this number involves delving into several key aspects:
- Definition: The square root of a number is a value that, when multiplied by itself, gives the original number.
- Properties: The square root of 340 is an irrational number with an infinite, non-repeating decimal expansion.
- Calculation: Various methods, such as long division and the use of calculators, can be employed to find the square root of 340.
- Applications: This value is utilized in engineering, physics, architecture, and various other scientific fields.
By understanding the square root of 340, one gains insight into its mathematical significance and practical applications. This article will guide you through the detailed calculation methods, properties, and real-world uses of \(\sqrt{340}\), providing a comprehensive understanding of this intriguing number.
Definition and Properties
The square root of a number is defined as a value that, when multiplied by itself, yields the original number. Mathematically, the square root of 340 is represented as \(\sqrt{340}\). This number falls between the integers 18 and 19, with an approximate value of 18.43908891.
Let's explore the properties of the square root of 340:
- Irrational Number: The square root of 340 is an irrational number, meaning it cannot be expressed as a fraction and its decimal form is non-terminating and non-repeating.
- Decimal Expansion: The approximate decimal value of \(\sqrt{340}\) is 18.43908891, but it continues infinitely without repeating.
- Prime Factorization: The prime factorization of 340 is \(2^2 \times 5 \times 17\). This factorization is useful in understanding the roots of 340, although it does not simplify the square root in this case.
- Approximation Methods: The square root of 340 can be approximated using various methods such as the long division method, Newton's method, or using a calculator.
The properties of \(\sqrt{340}\) provide insight into its mathematical behavior and its significance in different contexts. Understanding these properties is essential for applications in science, engineering, and mathematics.
Approximation Methods
There are several methods to approximate the square root of 340. Each method varies in complexity and precision. Here, we will discuss three common approximation techniques: the long division method, Newton's method, and the use of a calculator.
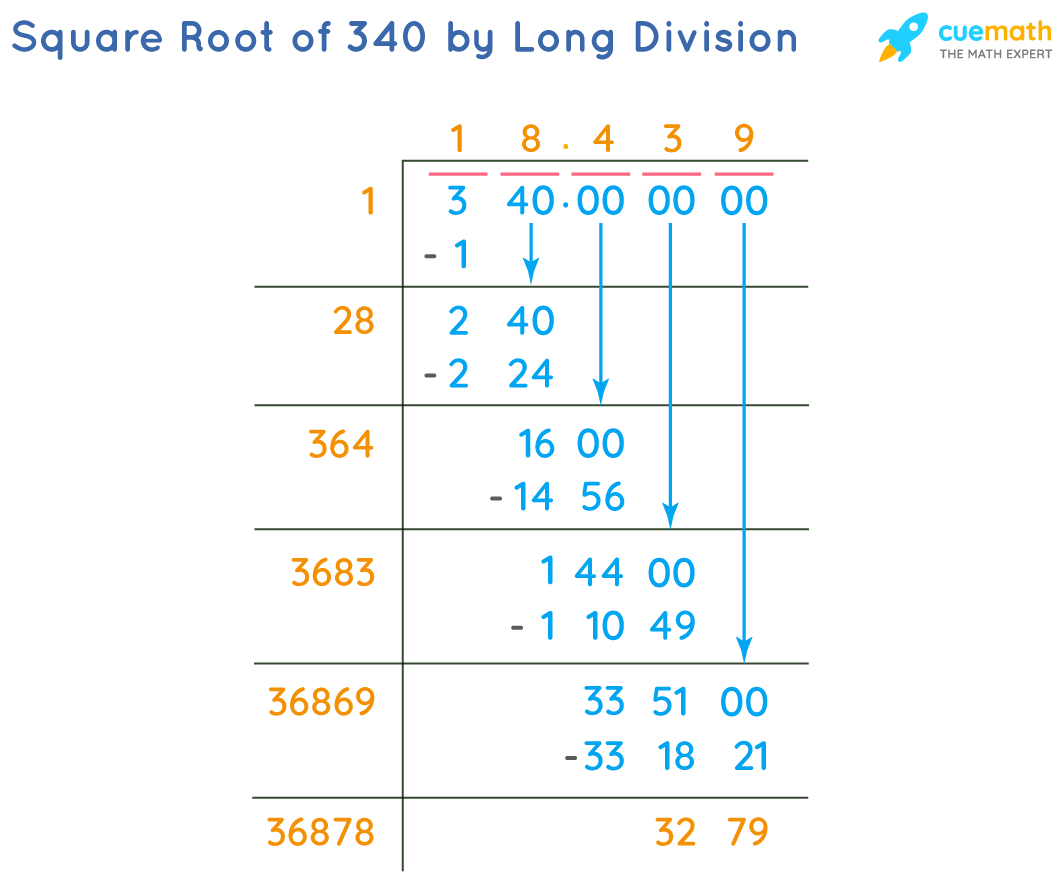
Long Division Method
The long division method is a manual process that provides an accurate approximation of the square root. Follow these steps:
- Pair the Digits: Start by pairing the digits of 340 from right to left. For 340, we have (3) and (40).
- Initial Estimate: Find the largest integer whose square is less than or equal to the first pair (3). This is 1, since \(1^2 = 1\).
- Divide and Subtract: Subtract 1 from 3, giving a remainder of 2. Bring down the next pair (40), making it 240.
- Find the Next Digit: Double the current quotient (1) to get 2. Find a digit (X) such that \(2X \times X \leq 240\). The correct digit is 8 (28 × 8 = 224).
- Repeat: Subtract 224 from 240 to get 16. Bring down 00, making it 1600. Repeat the process to get more decimal places.
Newton's Method
Newton's method, also known as the Newton-Raphson method, is an iterative approach for approximating roots. Follow these steps:
- Initial Guess: Choose an initial guess close to the actual square root. For example, 18.
- Iterative Formula: Apply the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{340}{x_n} \right) \).
- Convergence: Continue the iteration until the values converge. For instance:
- First iteration: \( x_1 = \frac{1}{2} \left( 18 + \frac{340}{18} \right) \approx 18.444 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 18.444 + \frac{340}{18.444} \right) \approx 18.439 \)
- Continue until desired precision is reached.
Using a Calculator
For a quick and accurate approximation, using a calculator is the simplest method:
- Enter the number 340.
- Press the square root (√) button.
- The calculator displays the result: approximately 18.43908891.
Comparison Table
| Method | Result | Precision |
| Long Division | Approximately 18.439 | Moderate |
| Newton's Method | Approximately 18.43908891 | High |
| Calculator | 18.43908891 | High |
Each method provides a reliable approximation of the square root of 340, with varying levels of complexity and precision. Choose the method that best fits your needs and available tools.
Prime Factorization
Prime factorization is the process of expressing a number as the product of its prime factors. Understanding the prime factorization of a number helps in various mathematical calculations, including finding the square root. Here, we will determine the prime factorization of 340 and explore its implications.
Steps to Find Prime Factorization of 340
- Divide by the Smallest Prime: Start by dividing 340 by the smallest prime number, which is 2.
- \(340 \div 2 = 170\)
- Continue with the Quotient: Divide the quotient (170) by 2.
- \(170 \div 2 = 85\)
- Move to the Next Prime: Since 85 is not divisible by 2, proceed to the next smallest prime, which is 5.
- \(85 \div 5 = 17\)
- Check for Further Division: 17 is a prime number and cannot be divided further by any other primes.
Prime Factorization of 340
The prime factors of 340 can be written as:
\(340 = 2^2 \times 5 \times 17\)
Using Prime Factorization to Understand the Square Root
The prime factorization of 340 helps us understand its square root:
- We can express \(\sqrt{340}\) using its prime factors:
- \(\sqrt{340} = \sqrt{2^2 \times 5 \times 17}\)
- This simplifies to \(\sqrt{2^2} \times \sqrt{5} \times \sqrt{17} = 2 \times \sqrt{5 \times 17} = 2 \times \sqrt{85}\)
However, since 85 is not a perfect square, the square root remains an irrational number, approximately 18.43908891.
Summary Table
| Number | Prime Factors |
| 340 | 2, 2, 5, 17 |
| Square Root Simplification | 2 × \(\sqrt{85}\) |
Understanding the prime factorization of 340 provides deeper insights into its properties and helps in performing precise mathematical calculations.

Irrational Number Explanation
The square root of 340 is an irrational number. To understand why it is irrational, we need to explore the concept of irrational numbers and the properties that make \(\sqrt{340}\) fall into this category.
Definition of Irrational Numbers
An irrational number is a number that cannot be expressed as a simple fraction, meaning it cannot be written as \(\frac{a}{b}\), where \(a\) and \(b\) are integers and \(b \neq 0\). Instead, irrational numbers have non-terminating, non-repeating decimal expansions.
Why \(\sqrt{340}\) is Irrational
Let's examine why \(\sqrt{340}\) is an irrational number:
- Prime Factorization: The prime factorization of 340 is \(2^2 \times 5 \times 17\).
- When we take the square root of 340, it can be written as \(\sqrt{340} = \sqrt{2^2 \times 5 \times 17} = 2 \times \sqrt{85}\).
- \(\sqrt{85}\) cannot be simplified further as 85 is not a perfect square, making it an irrational number.
- Non-repeating Decimal Expansion: The decimal expansion of \(\sqrt{340}\) is approximately 18.43908891, and it continues infinitely without repeating. This non-repeating nature confirms its irrationality.
Properties of Irrational Numbers
- Non-terminating Decimals: Irrational numbers have decimal expansions that go on forever without repeating.
- Cannot be Exactly Represented as Fractions: Unlike rational numbers, irrational numbers cannot be precisely written as a ratio of two integers.
- Unique Characteristics: Each irrational number is unique and does not have a repeating pattern in its decimal representation.
Examples of Irrational Numbers
Other common examples of irrational numbers include:
- \(\pi\) (Pi) - approximately 3.14159
- \(e\) (Euler's Number) - approximately 2.71828
- \(\sqrt{2}\) - approximately 1.41421
Conclusion
The square root of 340 is an irrational number because its decimal expansion is non-terminating and non-repeating, and it cannot be expressed as a fraction. Understanding the nature of irrational numbers helps us appreciate the complexity and beauty of mathematics.
Real-life Applications
The square root of 340, approximately 18.439, has several practical applications in various fields such as architecture, physics, computer graphics, and finance. Here are some specific examples:
-
Architecture and Design:
In architecture, knowing the square root of an area helps in determining the dimensions of a space. For instance, if an architect is designing a square room with an area of 340 square meters, the side length of the room would be approximately 18.439 meters.
-
Physics and Engineering:
In physics, the concept of root mean square (RMS) is crucial for calculating various parameters. For example, RMS values are used to determine the intensity of alternating currents or to analyze stress and strain in materials.
-
Computer Graphics:
In computer graphics, calculating the distance between points often requires square roots. For example, to find the diagonal distance across a square plot of land with an area of 340 square units, the length of each side can be found using the square root of 340.
-
Finance:
In finance, square roots are used in risk assessment models and to calculate the standard deviation of investment returns. This helps in understanding the volatility of financial instruments.
-
Education:
Square roots are fundamental in teaching concepts in geometry, algebra, and calculus. For instance, solving quadratic equations often involves using square roots.
These applications demonstrate the importance of understanding square roots and their practical utility in solving real-world problems.
Step-by-step Calculation
Calculating the square root of 340 involves a few steps to ensure accuracy. Here is a detailed step-by-step guide:
-
Initial Estimation: Identify two perfect squares between which 340 falls. These are 324 (182) and 361 (192). Since 340 is closer to 324, we can estimate that the square root of 340 is slightly above 18.
-
Refinement Using Average Method:
- Divide 340 by our initial estimate (18):
- Average this result with the initial estimate to refine the approximation:
\[\frac{340}{18} \approx 18.888\]
\[\frac{18 + 18.888}{2} \approx 18.444\]
-
Iterative Method (Babylonian Method): This method uses the formula:
\[\text{New estimate} = \frac{1}{2} \left( \text{Current estimate} + \frac{340}{\text{Current estimate}} \right)\]
- Starting with our refined estimate (18.444):
\[\text{New estimate} = \frac{1}{2} \left( 18.444 + \frac{340}{18.444} \right) \approx 18.439\]
-
Final Verification: Square the final estimate to verify accuracy:
\[18.439^2 \approx 340\]
This iterative process ensures that the square root calculation is accurate, with the final approximation of the square root of 340 being approximately 18.439.
Using a Calculator
Calculating the square root of 340 using a calculator is straightforward. Here's a step-by-step guide to help you through the process:
-
Choose the Right Calculator: Ensure you have a calculator with a square root function. Scientific calculators, graphing calculators, and most modern smartphones have this feature. Look for a button marked with the radical symbol (√) or labeled as "sqrt" or "x√y".
-
Turn on the Calculator: If you're using a physical calculator, power it on. If you're using a smartphone or an online calculator, open the app or website.
-
Enter the Number: Key in the number 340. Ensure you enter it correctly to avoid errors.
-
Execute the Square Root Function: Press the square root button (√). The calculator will process the input and display the result. If your calculator does not have a square root button, you might need to use the exponentiation method by pressing the exponentiation button (^) and entering 0.5 as the exponent.
-
Read the Result: The display will show the square root of 340. For example, it should display approximately 18.4390889146.
Using a calculator simplifies the process of finding square roots, especially for non-perfect squares like 340. This method ensures accuracy and saves time compared to manual calculations.
Square Root Simplification
Simplifying the square root of a number involves breaking it down into its prime factors and pairing them appropriately to extract perfect squares. Here's a detailed, step-by-step process to simplify the square root of 340:
-
Prime Factorization: Start by finding the prime factors of 340. The prime factors of 340 are:
- 340 ÷ 2 = 170
- 170 ÷ 2 = 85
- 85 ÷ 5 = 17
- 17 is a prime number.
So, the prime factorization of 340 is \(2^2 \times 5^1 \times 17^1\).
-
Group the Pairs: Identify and group the pairs of prime factors. In this case, \(2^2\) forms a pair, while 5 and 17 remain unpaired.
\(\sqrt{340} = \sqrt{2^2 \times 5 \times 17}\)
-
Extract the Square Roots: Take the square root of the paired factors and place them outside the radical sign. For the remaining factors, keep them inside the radical.
\(\sqrt{2^2 \times 5 \times 17} = 2 \sqrt{5 \times 17}\)
So, the simplified form is \(2 \sqrt{85}\).
This method helps simplify the square root expression to its most reduced form, making it easier to handle in further calculations.
Comparing with Other Square Roots
Comparing the square root of 340 with other square roots can provide insight into its relative size and properties. Below are some comparisons with other notable square roots:
- Square Root of 100 (10): The square root of 340, approximately 18.439, is significantly larger than the square root of 100, which is 10. This comparison helps to understand that 340 is more than three times larger than 100 when squared.
- Square Root of 225 (15): The square root of 225 is 15. The square root of 340 is greater than 15, indicating that 340 is a larger number than 225 when squared, but not by a large margin.
- Square Root of 400 (20): The square root of 400 is 20. The square root of 340 falls slightly below this value, showing that 340 is a bit smaller than 400 when squared.
- Square Root of 500 (22.36): The square root of 500 is approximately 22.36. This indicates that 340 is significantly smaller than 500 when squared.
To put this into perspective, here is a table comparing the square roots of these values:
| Number | Square Root |
|---|---|
| 100 | 10 |
| 225 | 15 |
| 340 | 18.439 |
| 400 | 20 |
| 500 | 22.36 |
These comparisons highlight that the square root of 340 is closer to the square root of 400 than it is to the square roots of 225 and 500. Such comparisons can be useful in various mathematical and real-world applications where understanding the relative magnitude of numbers is important.
Historical Context
The concept of square roots dates back to ancient civilizations. The Babylonians are known to have used methods for estimating square roots as early as 2000 BCE. They employed a form of the iterative method, similar to what we now know as the Babylonian method or Heron's method, to approximate square roots.
In ancient Greece, the Pythagoreans made significant contributions to the understanding of square roots, especially through the Pythagorean theorem, which inherently involves the square root operation. This theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides, leading to the need to understand and calculate square roots.
The concept of irrational numbers, which includes many square roots, was a major development in Greek mathematics. The discovery that the square root of 2 could not be expressed as a fraction was a pivotal moment that expanded the number system beyond rationals. This discovery is attributed to the Pythagorean Hippasus.
During the medieval period, Islamic mathematicians preserved and expanded upon Greek and Indian mathematical knowledge. The Persian scholar Al-Khwarizmi contributed to algebra, providing methods for solving quadratic equations that implicitly involve finding square roots.
In the Renaissance, European mathematicians like Rafael Bombelli began to systematically study complex numbers, which include square roots of negative numbers. The development of algebraic notation and the symbolic representation of square roots (\( \sqrt{} \)) during this period made calculations more systematic and widely accessible.
By the 17th century, mathematicians like Isaac Newton further refined methods for approximating square roots through numerical analysis techniques. The advent of calculus provided new tools for understanding and computing square roots and other mathematical functions.
In modern times, the calculation of square roots has been greatly facilitated by electronic calculators and computer algorithms. However, the historical journey of the square root highlights its fundamental importance in mathematics and its continuous evolution across different cultures and eras.
Common Mistakes
When working with the square root of 340, there are several common mistakes that students and learners might encounter. Here are some of the most frequent errors and how to avoid them:
-
Incorrect Simplification:
One of the most common mistakes is incorrectly simplifying the square root. For example, thinking that \(\sqrt{340} = 18.44\) (since 340 is close to 18 squared) is incorrect. The correct simplification process involves recognizing that 340 can be factored into 4 and 85, so \(\sqrt{340} = \sqrt{4 \times 85} = \sqrt{4} \times \sqrt{85} = 2\sqrt{85}\).
-
Incorrect Distribution:
Another mistake involves distributing the square root incorrectly over sums or differences. The square root of a sum is not the sum of the square roots, i.e., \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\). For instance, \(\sqrt{340 + 60} \neq \sqrt{340} + \sqrt{60}\).
-
Misplacing Decimal Points:
When approximating the square root, ensure the decimal point is correctly placed. For example, approximating \(\sqrt{340}\) as 18.44 instead of the more accurate 18.439 is a typical mistake.
-
Using Inexact Values:
Often, learners use rounded values too early in their calculations. For precise results, keep the values exact until the final step. Using \(\sqrt{340} \approx 18.439\) for calculations, rather than 18.4, ensures better accuracy.
-
Ignoring Negative Roots:
When solving equations involving square roots, remember to consider both the positive and negative roots. While the principal square root of 340 is positive, in some contexts, \(\pm \sqrt{340}\) may be relevant.
By being aware of these common pitfalls and practicing careful calculation methods, one can avoid these errors and work more accurately with square roots.

FAQs
Here are some frequently asked questions about the square root of 340:
- What is the square root of 340?
- Is the square root of 340 a rational number?
- Can the square root of 340 be simplified?
- What are some methods to calculate the square root of 340?
- How is the square root of 340 used in real-life applications?
- What are some common mistakes when calculating the square root of 340?
The square root of 340 is approximately 18.439088.
No, the square root of 340 is an irrational number because it cannot be expressed as a simple fraction.
Yes, the square root of 340 can be simplified to 2√85.
You can use methods such as long division, prime factorization, or a calculator to find the square root of 340.
The square root of 340 can be used in various fields such as engineering, physics, and architecture where precise measurements are required.
Common mistakes include incorrect rounding, using the wrong method for calculation, or not simplifying the square root properly.
Conclusion
The square root of 340 is approximately 18.439. This number represents a value that, when multiplied by itself, equals 340. Understanding the square root of 340 involves exploring its properties, calculation methods, and applications.
Throughout this guide, we have covered various aspects of the square root of 340, including its mathematical significance, real-life applications, and historical context. We've also detailed the methods to calculate it, both manually and using a calculator, and discussed common mistakes to avoid.
By delving into the prime factorization and approximation techniques, we've highlighted the importance of square roots in both theoretical and practical contexts. Additionally, comparing the square root of 340 with other square roots has provided a broader perspective on its relative value.
Overall, the square root of 340 is an essential mathematical concept that demonstrates the interplay between numbers and their roots. Whether for academic purposes or practical applications, understanding this square root enhances our comprehension of mathematical principles and their real-world implications.
Căn bậc hai của 340