Topic square root of 32 in radical form: Discover how to simplify the square root of 32 in radical form with our easy-to-follow guide. This article breaks down the steps to express √32 in its simplest radical form, providing clear explanations and practical examples. Perfect for students and math enthusiasts looking to enhance their understanding of radicals and square roots.
Table of Content
- Square Root of 32 in Radical Form
- Introduction to Square Roots
- Understanding Radical Expressions
- Prime Factorization
- Simplifying Square Roots
- Step-by-Step Simplification of √32
- Breaking Down 32 into Prime Factors
- Pairing Prime Factors
- Extracting Factors from the Radical
- Final Simplified Form of √32
- Verification of Simplified Form
- Common Mistakes to Avoid
- Practical Applications of Simplifying Radicals
- Additional Practice Problems
- Frequently Asked Questions
- Conclusion
- YOUTUBE:
Square Root of 32 in Radical Form
The square root of 32 can be expressed in its simplest radical form. To do this, we need to find the prime factorization of 32 and simplify the radical.
Prime Factorization of 32
First, let's determine the prime factors of 32:
- 32 is divisible by 2: 32 ÷ 2 = 16
- 16 is divisible by 2: 16 ÷ 2 = 8
- 8 is divisible by 2: 8 ÷ 2 = 4
- 4 is divisible by 2: 4 ÷ 2 = 2
- 2 is divisible by 2: 2 ÷ 2 = 1
Thus, the prime factorization of 32 is:
32 = 2 × 2 × 2 × 2 × 2 = 25
Simplifying the Radical
To simplify the square root of 32, we look for pairs of prime factors:
- We can pair up the factors: \(2 \times 2\) and \(2 \times 2\)
- This gives us two pairs of 2s, which can be taken out of the radical:
- \(\sqrt{2 \times 2 \times 2 \times 2 \times 2} = \sqrt{(2 \times 2) \times (2 \times 2) \times 2} = 2 \times 2 \times \sqrt{2} = 4\sqrt{2}\)
Therefore, the square root of 32 in its simplest radical form is:
\(\sqrt{32} = 4\sqrt{2}\)
This is the simplified form of the square root of 32, expressed as \(4\sqrt{2}\).

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics and involves finding a number that, when multiplied by itself, equals the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\).
Square roots can be represented using the radical symbol \( \sqrt{} \). The expression \( \sqrt{a} \) denotes the square root of \( a \). For instance, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
Square roots are essential for solving quadratic equations, simplifying expressions, and understanding various mathematical concepts. They can be either perfect squares or irrational numbers, depending on whether the number under the radical is a perfect square.
Here's a step-by-step breakdown of key points about square roots:
- Definition: The square root of a number \( a \) is a value \( x \) such that \( x^2 = a \).
- Notation: The square root of \( a \) is denoted as \( \sqrt{a} \).
- Perfect Squares: If \( a \) is a perfect square, \( \sqrt{a} \) is an integer. For example, \( \sqrt{25} = 5 \).
- Irrational Numbers: If \( a \) is not a perfect square, \( \sqrt{a} \) is an irrational number. For instance, \( \sqrt{2} \) is approximately 1.414 and cannot be expressed as a precise fraction.
- Simplifying Radicals: Simplifying square roots involves expressing the number under the radical in its simplest form, often by breaking it down into prime factors.
Understanding square roots and their properties is crucial for higher-level math topics, including algebra, calculus, and beyond. The ability to simplify and manipulate square roots allows for more straightforward solutions to complex mathematical problems.
Understanding Radical Expressions
Radical expressions involve roots, such as square roots, cube roots, and higher-order roots. These expressions are an essential part of algebra and higher mathematics, allowing us to simplify and solve various types of equations.
A radical expression generally consists of a radical symbol \( \sqrt{} \) with a radicand (the number or expression inside the radical) and, sometimes, an index (which specifies the root). For example, in \( \sqrt[3]{8} \), 3 is the index, and 8 is the radicand, representing the cube root of 8.
Here are key points to understand about radical expressions:
- Radicand: The number or expression inside the radical symbol. For instance, in \( \sqrt{32} \), 32 is the radicand.
- Index: The small number written just outside and above the radical symbol, indicating the degree of the root. If the index is 2, it represents a square root, which is typically not written. For cube roots, the index is 3, and so on.
- Simplifying Radicals: To simplify a radical expression, factorize the radicand into its prime factors and look for pairs (for square roots) or groups (for higher-order roots). For example, \( \sqrt{32} \) can be simplified as \( 4\sqrt{2} \) by breaking it down into prime factors.
- Rationalizing the Denominator: If a radical appears in the denominator of a fraction, multiply the numerator and the denominator by a suitable radical to eliminate the radical from the denominator. For instance, to rationalize \( \frac{1}{\sqrt{2}} \), multiply by \( \frac{\sqrt{2}}{\sqrt{2}} \) to get \( \frac{\sqrt{2}}{2} \).
- Operations with Radicals: Radicals can be added, subtracted, multiplied, and divided, but only like radicals (same index and radicand) can be directly added or subtracted. For multiplication and division, use the properties of exponents to combine the radicands.
Let's look at a simplified example for better understanding:
- Example: Simplify \( \sqrt{32} \)
- Step 1: Factorize 32 into prime factors: \( 32 = 2 \times 2 \times 2 \times 2 \times 2 \)
- Step 2: Pair the factors: \( \sqrt{32} = \sqrt{(2 \times 2) \times (2 \times 2) \times 2} \)
- Step 3: Simplify by taking out pairs: \( \sqrt{32} = 2 \times 2 \times \sqrt{2} = 4\sqrt{2} \)
Understanding and simplifying radical expressions is fundamental for solving algebraic equations, working with functions, and exploring higher mathematics concepts. Mastery of these skills ensures a strong mathematical foundation.
Prime Factorization
Prime factorization is the process of breaking down a composite number into a product of its prime factors. This method is crucial for simplifying radicals, such as finding the square root of 32 in radical form. Let's go through the steps to perform prime factorization:
To factorize 32, we need to divide it by the smallest prime number, 2, repeatedly until we are left with 1:
- Step 1: Divide 32 by 2:
- 32 ÷ 2 = 16
- Step 2: Divide 16 by 2:
- 16 ÷ 2 = 8
- Step 3: Divide 8 by 2:
- 8 ÷ 2 = 4
- Step 4: Divide 4 by 2:
- 4 ÷ 2 = 2
- Step 5: Divide 2 by 2:
- 2 ÷ 2 = 1
Thus, the prime factorization of 32 is:
\( 32 = 2 \times 2 \times 2 \times 2 \times 2 = 2^5 \)
We can summarize the prime factorization process in a table for clarity:
| Step | Operation | Result |
|---|---|---|
| 1 | 32 ÷ 2 | 16 |
| 2 | 16 ÷ 2 | 8 |
| 3 | 8 ÷ 2 | 4 |
| 4 | 4 ÷ 2 | 2 |
| 5 | 2 ÷ 2 | 1 |
By understanding and applying prime factorization, we can simplify complex radical expressions efficiently. For example, knowing that \( 32 = 2^5 \) helps us simplify \( \sqrt{32} \) to \( 4\sqrt{2} \), as detailed in the following sections.
Simplifying Square Roots
Simplifying square roots involves reducing the expression to its simplest radical form. To simplify the square root of a number, you need to identify and factor out any perfect square factors. Here's a step-by-step guide to simplifying square roots:
- Identify the Prime Factors:
First, break down the number inside the square root into its prime factors. For example, for √32, the prime factors are 2, 2, 2, 2, and 2, as 32 = 2 × 2 × 2 × 2 × 2.
- Pair the Prime Factors:
Next, pair the prime factors. For √32, the pairs are (2 × 2) and (2 × 2), with one 2 left over. This can be represented as:
√32 = √(2 × 2 × 2 × 2 × 2)
- Extract the Pairs:
Each pair of prime factors can be taken out of the radical. For every pair of 2's, one 2 is taken out of the square root. This step simplifies the expression as follows:
√32 = √(2 × 2) × √(2 × 2) × √2
√32 = 2 × 2 × √2
- Multiply the Extracted Numbers:
Finally, multiply the numbers taken out of the radical:
2 × 2 = 4
So, √32 = 4√2
Therefore, the simplified radical form of √32 is 4√2. This method can be applied to simplify any square root by following these steps: factorize, pair the prime factors, and then extract and multiply the pairs.
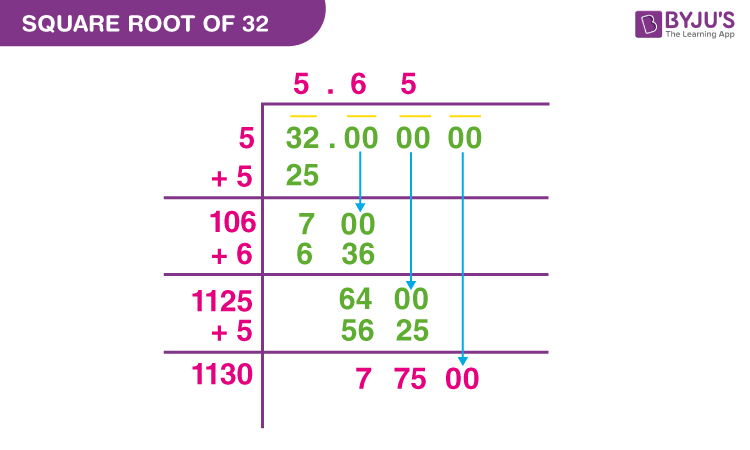
Step-by-Step Simplification of √32
Simplifying the square root of 32 involves a few key steps. Here's a detailed breakdown:
-
Prime Factorization:
First, we need to find the prime factors of 32. The prime factorization of 32 is:
\[
32 = 2 \times 2 \times 2 \times 2 \times 2 = 2^5
\] -
Group the Prime Factors:
Next, we group the prime factors in pairs:
\[
\sqrt{32} = \sqrt{2^5} = \sqrt{(2^2) \times (2^2) \times 2}
\] -
Extract the Pairs:
We know that the square root of a product is the product of the square roots. Therefore, we can extract the pairs from under the radical:
\[
\sqrt{(2^2) \times (2^2) \times 2} = \sqrt{2^2} \times \sqrt{2^2} \times \sqrt{2}
\]Simplifying the square roots of the pairs gives us:
\[
\sqrt{2^2} = 2
\] -
Combine the Results:
Now, we combine the results to get the simplified form:
\[
\sqrt{32} = 2 \times 2 \times \sqrt{2} = 4\sqrt{2}
\]
Therefore, the simplified form of \(\sqrt{32}\) is \(4\sqrt{2}\).
Breaking Down 32 into Prime Factors
To simplify the square root of 32, we first need to break it down into its prime factors. This step is essential because it allows us to simplify the expression under the radical sign.
- Start by identifying the prime factors of 32.
- 32 is an even number, so it is divisible by 2.
- Divide 32 by 2:
- 32 ÷ 2 = 16
- 16 is also an even number, so continue dividing by 2:
- 16 ÷ 2 = 8
- 8 ÷ 2 = 4
- 4 ÷ 2 = 2
- 2 ÷ 2 = 1
Thus, the prime factorization of 32 is:
\[ 32 = 2 \times 2 \times 2 \times 2 \times 2 = 2^5 \]
Next, we group these prime factors into pairs, as each pair of factors can be simplified under the square root:
\[ \sqrt{32} = \sqrt{2 \times 2 \times 2 \times 2 \times 2} = \sqrt{(2 \times 2) \times (2 \times 2) \times 2} \]
This simplifies to:
\[ \sqrt{32} = \sqrt{(2^2) \times (2^2) \times 2} \]
Since the square root of \( 2^2 \) is 2, we can extract these pairs from under the radical:
\[ \sqrt{32} = \sqrt{2^2} \times \sqrt{2^2} \times \sqrt{2} = 2 \times 2 \times \sqrt{2} \]
Simplifying further, we get:
\[ \sqrt{32} = 4\sqrt{2} \]
Therefore, the square root of 32 in its simplest radical form is \( 4\sqrt{2} \).
Pairing Prime Factors
To simplify the square root of 32, we first need to break it down into its prime factors, and then pair these factors.
- Start by expressing 32 as a product of prime factors:
\( 32 = 2 \times 2 \times 2 \times 2 \times 2 \)
- Next, pair the prime factors:
- Pair 1: \( 2 \times 2 \)
- Pair 2: \( 2 \times 2 \)
- Leftover: \( 2 \)
- Rewrite the pairs under the square root:
\( \sqrt{32} = \sqrt{(2 \times 2) \times (2 \times 2) \times 2} \)
- Since the square root of a pair \( (2 \times 2) \) is 2, we extract these pairs from under the radical:
\( \sqrt{32} = 2 \times 2 \times \sqrt{2} \)
- Multiply the extracted factors:
\( 2 \times 2 = 4 \)
- Combine the result with the remaining factor under the square root:
\( \sqrt{32} = 4\sqrt{2} \)
Therefore, the simplified form of the square root of 32 is \( 4\sqrt{2} \).
Extracting Factors from the Radical
To simplify the square root of 32, we need to extract factors from under the radical. This involves using the prime factors we identified earlier. Let's follow the steps to extract these factors:
- Recall that the prime factorization of 32 is \(2 \times 2 \times 2 \times 2 \times 2\), or \(2^5\).
- Group the factors into pairs. Since 32 has five 2's, we can form two pairs of 2's, with one 2 left over:
\(\sqrt{32} = \sqrt{2^2 \times 2^2 \times 2} = \sqrt{(2^2) \times (2^2) \times 2}\)
- Each pair of 2's can be simplified to a single 2 outside the radical:
\(\sqrt{(2^2) \times (2^2) \times 2} = 2 \times 2 \times \sqrt{2}\)
- Combine the factors outside the radical:
\(2 \times 2 = 4\)
- Thus, the simplified form of \(\sqrt{32}\) is:
\(4 \sqrt{2}\)
This process of extracting factors helps in simplifying the square root of non-perfect square numbers efficiently. Now, we have \(\sqrt{32} = 4 \sqrt{2}\), which is the simplest radical form.
Final Simplified Form of √32
To find the final simplified form of the square root of 32, we start by breaking down 32 into its prime factors. We have already determined that:
- 32 = 2 × 2 × 2 × 2 × 2
Next, we pair the prime factors:
- (2 × 2) × (2 × 2) × 2
Each pair of 2's can be taken out of the radical as a single 2:
- √(2 × 2) = 2
- √(2 × 2) = 2
So, we can write:
Multiplying the extracted factors, we get:
Therefore, the final simplified form of √32 is:
In conclusion, the square root of 32 simplifies to 4√2.
Verification of Simplified Form
To verify the simplified form of the square root of 32, we need to ensure that the simplification process is correct and that the simplified form, \(4\sqrt{2}\), is indeed accurate.
- Recall the simplified form:
- We simplified \(\sqrt{32}\) to \(4\sqrt{2}\).
- Verify by squaring both sides:
- Square \(4\sqrt{2}\): \[ (4\sqrt{2})^2 = 4^2 \cdot (\sqrt{2})^2 = 16 \cdot 2 = 32 \]
- Since the original number was 32, this confirms the simplified form is correct.
- Check with decimal approximation:
- Calculate \(4 \times \sqrt{2}\) using an approximate value for \(\sqrt{2}\) (approximately 1.414): \[ 4 \times 1.414 = 5.656 \]
- Compare this with the decimal value of \(\sqrt{32}\), which is approximately 5.6569. The values match closely, further verifying our simplified form.
Thus, the simplified form of \(\sqrt{32} = 4\sqrt{2}\) is verified both algebraically and by decimal approximation.
Common Mistakes to Avoid
When simplifying radicals, it's crucial to avoid common mistakes that can lead to incorrect results. Here are some typical pitfalls to watch out for:
- Forgetting to simplify completely: Ensure that you have factored the number under the radical sign into its prime factors and have extracted all possible square roots. Incomplete simplification can lead to errors.
- Skipping prime factorization: Skipping this step can prevent you from seeing which square roots can be extracted. Always break down the number into its prime factors first.
- Misunderstanding the square root of a product: Remember that the square root of a product (e.g., √(ab)) equals the product of the square roots (√a * √b). Confusion here can lead to incorrect simplification.
- Overlooking the need to simplify further: After extracting square factors, check if the radical or the number outside the radical can be simplified more.
- Confusing addition and multiplication under the radical: A common misconception is thinking that √a + √b equals √(a + b). The square root of a sum is not the sum of the square roots.
- Applying incorrect operations on radicals: Ensure that you're applying the correct arithmetic operations. The rules for adding, subtracting, multiplying, and dividing radicals are specific and must be followed accurately.
By being mindful of these common mistakes and focusing on the correct simplification procedures, you can enhance your proficiency in working with radicals and ensure that your mathematical expressions are simplified correctly.
Practical Applications of Simplifying Radicals
Simplifying radicals is not just a mathematical exercise; it has practical applications in various fields. Here are some examples:
- Geometry and Trigonometry:
In geometry, simplified radicals are used to find the lengths of sides in right triangles. For example, in a 45-45-90 triangle, the side lengths are in the ratio \(1:1:\sqrt{2}\). This means that if one leg is 1 unit, the hypotenuse will be \(\sqrt{2}\) units.
- Physics:
Radical expressions appear in various physics formulas. For instance, the distance between two points in a 2D or 3D space can be calculated using the distance formula derived from the Pythagorean theorem:
- Engineering:
Engineers often use radicals when calculating forces and distances. For example, in civil engineering, the calculation of forces in structures can involve square roots.
- Computer Graphics:
In computer graphics, radicals are used to calculate distances and create realistic graphics. For instance, the distance formula helps in rendering scenes correctly by determining how objects should be displayed relative to each other.
- Construction:
In construction, simplifying radicals can help in making precise measurements for cutting materials and ensuring structures are built accurately.
By understanding how to simplify radicals, you can apply this knowledge to solve real-world problems efficiently.

Additional Practice Problems
Here are some additional practice problems to help you master the simplification of square roots:
- Simplify √50
- Simplify √72
- Simplify √18
- Simplify √75
- Simplify √45
Solutions:
- √50
- Prime factorization of 50: \( 50 = 2 \times 5^2 \)
- Pair the prime factors: \( 5^2 \)
- Extract the square root: \( 5 \sqrt{2} \)
- Answer: \( \sqrt{50} = 5\sqrt{2} \)
- √72
- Prime factorization of 72: \( 72 = 2^3 \times 3^2 \)
- Pair the prime factors: \( 2^2 \times 3^2 \)
- Extract the square root: \( 2 \times 3 \sqrt{2} \)
- Answer: \( \sqrt{72} = 6\sqrt{2} \)
- √18
- Prime factorization of 18: \( 18 = 2 \times 3^2 \)
- Pair the prime factors: \( 3^2 \)
- Extract the square root: \( 3 \sqrt{2} \)
- Answer: \( \sqrt{18} = 3\sqrt{2} \)
- √75
- Prime factorization of 75: \( 75 = 3 \times 5^2 \)
- Pair the prime factors: \( 5^2 \)
- Extract the square root: \( 5 \sqrt{3} \)
- Answer: \( \sqrt{75} = 5\sqrt{3} \)
- √45
- Prime factorization of 45: \( 45 = 3^2 \times 5 \)
- Pair the prime factors: \( 3^2 \)
- Extract the square root: \( 3 \sqrt{5} \)
- Answer: \( \sqrt{45} = 3\sqrt{5} \)
Frequently Asked Questions
- What is the square root of 32 in radical form?
The square root of 32 in radical form is \( \sqrt{32} = 4\sqrt{2} \).
- How do you simplify \( \sqrt{32} \) step by step?
- Prime factorize 32: \( 32 = 2^5 \).
- Rewrite \( \sqrt{32} \) using the prime factors: \( \sqrt{32} = \sqrt{2^5} \).
- Pair the prime factors: \( 2^5 = 2^4 \times 2 = (2^2)^2 \times 2 = 4^2 \times 2 \).
- Extract the square root of the paired factors: \( \sqrt{4^2 \times 2} = 4\sqrt{2} \).
- Thus, \( \sqrt{32} = 4\sqrt{2} \).
- Why can't \( \sqrt{32} \) be simplified to a whole number?
\( \sqrt{32} \) cannot be simplified to a whole number because 32 is not a perfect square. The simplified form \( 4\sqrt{2} \) is the closest simplified radical form.
- Can you provide an example of another similar simplification?
Sure! Let's simplify \( \sqrt{50} \):
- Prime factorize 50: \( 50 = 2 \times 5^2 \).
- Rewrite \( \sqrt{50} \) using the prime factors: \( \sqrt{50} = \sqrt{2 \times 5^2} \).
- Extract the square root of the paired factor: \( \sqrt{2 \times 5^2} = 5\sqrt{2} \).
- Thus, \( \sqrt{50} = 5\sqrt{2} \).
- What are the practical applications of simplifying square roots?
Simplifying square roots is useful in various fields such as engineering, physics, and architecture, where precise calculations are necessary. It helps in solving equations, analyzing wave functions, and determining lengths and distances in geometric shapes.
Conclusion
Understanding how to simplify the square root of 32 and other similar expressions is a valuable skill in mathematics. By breaking down numbers into their prime factors and pairing them appropriately, we can simplify square roots to their radical forms.
To recap the simplification process for \( \sqrt{32} \):
- Prime factorize 32: \( 32 = 2^5 \).
- Rewrite \( \sqrt{32} \) using the prime factors: \( \sqrt{32} = \sqrt{2^5} \).
- Pair the prime factors: \( 2^5 = 2^4 \times 2 = (2^2)^2 \times 2 = 4^2 \times 2 \).
- Extract the square root of the paired factors: \( \sqrt{4^2 \times 2} = 4\sqrt{2} \).
- Thus, \( \sqrt{32} = 4\sqrt{2} \).
This method can be applied to any non-perfect square to simplify its square root. Simplifying square roots helps in various mathematical computations, making equations easier to solve and understand.
By mastering this technique, you can enhance your problem-solving skills and apply these principles in practical applications across different fields. Keep practicing with various numbers to become more proficient in simplifying radicals.
Cách Đơn Giản Hóa Căn Bậc Hai của 32: Sqrt(32)
READ MORE:
Cách Đơn Giản Hóa Căn Bậc Hai của 32














