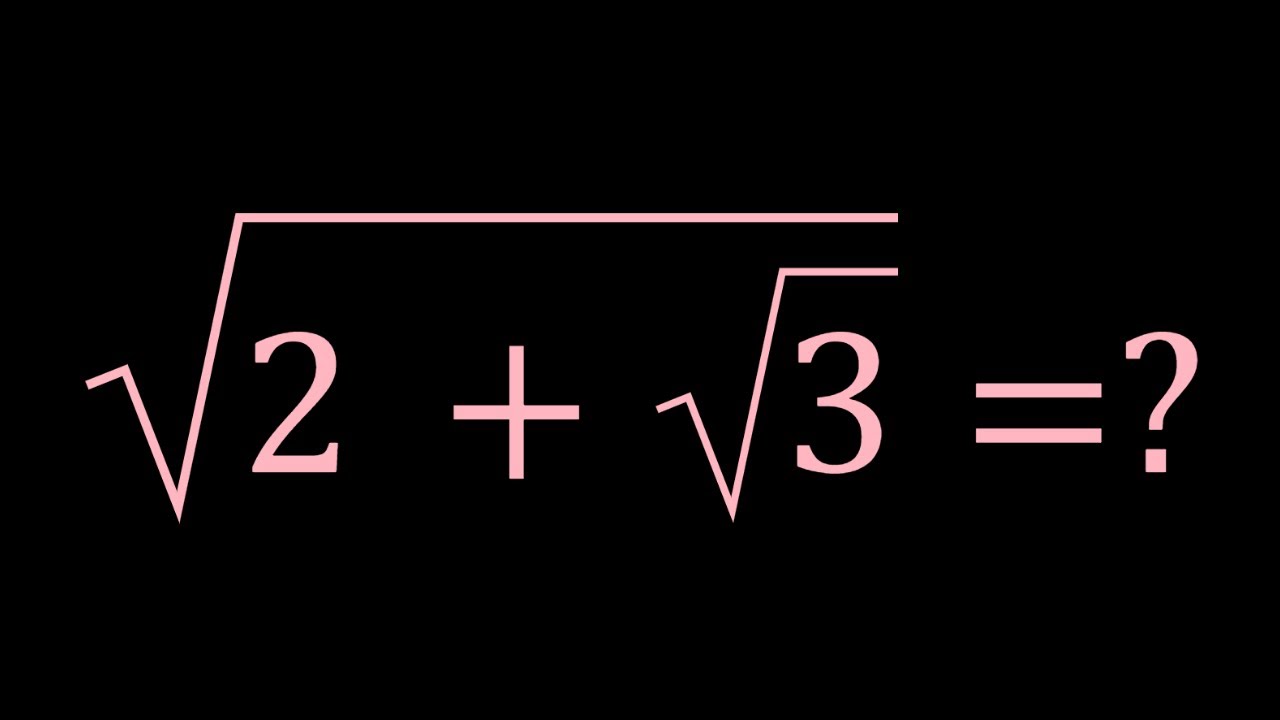Understanding the 352 Square Root: A Comprehensive Guide

The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 352, the square root is a value that satisfies this condition.

Exact Value

The exact square root of 352 can be expressed using the square root symbol:

\[\sqrt{352}\]

Approximate Value

The approximate value of the square root of 352 to three decimal places is:

\[\sqrt{352} \approx 18.761\]

Calculation Steps

To find the square root of 352, one can use the following methods:

• Using a Calculator

Prime Factorization Method

Prime factorization of 352 is:

352 = 2^5 \times 11

The square root of 352 using prime factorization is:

\[\sqrt{352} = \sqrt{2^5 \times 11} = 2^2 \times \sqrt{2 \times 11} = 4 \sqrt{22}\]

Long Division Method

The long division method provides a systematic way to find the square root:

1. Pair the digits of 352 from right to left.
2. Find the largest number whose square is less than or equal to 3. This is 1, with a remainder of 2.
3. Bring down the next pair of digits (52), making it 252.
4. Double the current quotient (1), which is 2. Find a digit X such that 2X × X is less than or equal to 252. This digit is 8, giving a quotient of 18 and a remainder of 16.
5. Repeat the process to get a more accurate value.

Verification

To verify the calculation:

\[18.761 \times 18.761 \approx 352\]

This confirms that the approximate value of \(\sqrt{352}\) is indeed 18.761.

Square roots are fundamental mathematical concepts that play a crucial role in various areas of mathematics and science. A square root of a number is a value that, when multiplied by itself, results in the original number. It is denoted by the radical symbol \(\sqrt{}\).

For example, the square root of 9 is 3 because \(3 \times 3 = 9\). Similarly, the square root of 16 is 4 because \(4 \times 4 = 16\). Square roots can be both positive and negative because both \(3 \times 3 = 9\) and \(-3 \times -3 = 9\).

Here is a step-by-step approach to understanding square roots:

1. Identify the number: Determine the number for which you want to find the square root.
2. Check for perfect squares: Check if the number is a perfect square (e.g., 1, 4, 9, 16, 25, etc.). Perfect squares have whole numbers as their square roots.
3. Prime factorization: If the number is not a perfect square, break it down into its prime factors to simplify the square root.
4. Use the radical symbol: Express the square root using the radical symbol \(\sqrt{}\) and simplify if possible.
5. Approximate the value: For non-perfect squares, use methods like the long division method or a calculator to approximate the square root.

Understanding square roots is essential for solving quadratic equations, understanding geometric properties, and working with complex numbers. Square roots also have practical applications in fields such as engineering, physics, and finance.

The concept of square roots is a cornerstone of mathematics, providing a foundation for various calculations and problem-solving techniques. The square root of a number is a value that, when multiplied by itself, yields the original number. It is symbolized by the radical sign \(\sqrt{}\).

For example, the square root of 25 is 5, because \(5 \times 5 = 25\). Similarly, the square root of 81 is 9, because \(9 \times 9 = 81\). Square roots can be both positive and negative since both \(5 \times 5 = 25\) and \(-5 \times -5 = 25\).

Here is a detailed breakdown of the concept:

1. Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). This can be written as:

   \[y = \sqrt{x}\]

2. Perfect Squares: Numbers like 1, 4, 9, 16, 25, etc., are called perfect squares because their square roots are whole numbers. For instance:
   • \(\sqrt{1} = 1\)
   • \(\sqrt{4} = 2\)
   • \(\sqrt{9} = 3\)
   • \(\sqrt{16} = 4\)
   • \(\sqrt{25} = 5\)
3. Non-Perfect Squares: Numbers that are not perfect squares do not have whole numbers as their square roots. For example, \(\sqrt{2}\), \(\sqrt{3}\), and \(\sqrt{5}\) are irrational numbers, meaning their decimal representation goes on forever without repeating.
4. Calculating Square Roots: There are several methods to find the square root of a number:
   • Prime Factorization: Break down the number into its prime factors and simplify using pairs of prime factors.
   • Long Division Method: A manual method to approximate the square root by iteratively guessing and refining the value.
   • Calculator: Modern calculators can quickly and accurately provide square root values.
5. Properties of Square Roots:
   • \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
   • \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
   • \(\sqrt{x^2} = |x|\) (absolute value of x)

Understanding square roots is essential for many mathematical operations and applications in science, engineering, and daily life. It helps in solving equations, analyzing geometric shapes, and understanding mathematical relationships.

The square root of a number is a value that, when multiplied by itself, equals the original number. It is denoted by the radical symbol \(\sqrt{}\) or as an exponent of \(1/2\). The mathematical definition can be expressed as:

\[ \sqrt{x} = y \text{ if and only if } y^2 = x \]

For any non-negative real number \(x\), there are two square roots: a positive root \(\sqrt{x}\) and a negative root \(-\sqrt{x}\). Here are the key aspects of the mathematical definition of square roots:

1. Non-Negative Numbers: For any non-negative number \(x\), the square root is defined as the non-negative number \(y\) such that \(y^2 = x\). For example:
   • \(\sqrt{16} = 4\) because \(4^2 = 16\)
   • \(\sqrt{25} = 5\) because \(5^2 = 25\)
2. Properties of Square Roots:
   • \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
   • \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) for \(b \neq 0\)
   • \(\sqrt{x^2} = |x|\) (the absolute value of \(x\))
3. Complex Numbers: For negative numbers, the square root is not a real number but a complex number. For example:

   \(\sqrt{-1} = i\), where \(i\) is the imaginary unit

4. Irrational Square Roots: Some numbers have square roots that are irrational, meaning their decimal representation is non-terminating and non-repeating. For instance:
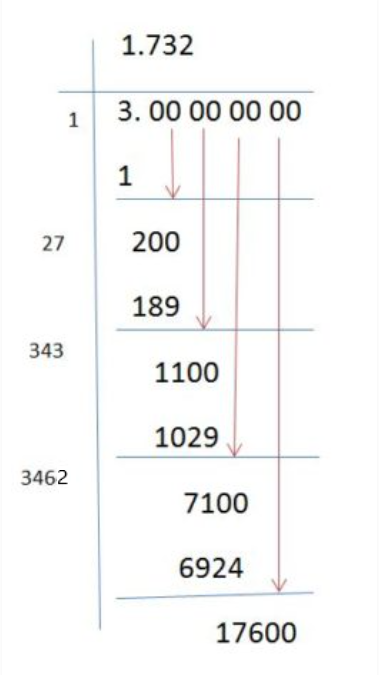
   • \(\sqrt{2} \approx 1.414\)
   • \(\sqrt{3} \approx 1.732\)
5. Rational Square Roots: Perfect squares have rational square roots, which can be expressed as a fraction or an integer. For example:
   • \(\sqrt{1} = 1\)
   • \(\sqrt{4} = 2\)
   • \(\sqrt{9} = 3\)

Understanding the mathematical definition of square roots is essential for various mathematical concepts and operations, including solving quadratic equations, simplifying expressions, and analyzing geometric properties.

Calculating square roots can be done through various methods, ranging from manual techniques to the use of calculators. Below are the most common methods for finding the square root of a number:

1. Prime Factorization Method:

   This method involves breaking down the number into its prime factors and simplifying. Here are the steps:

   • Find the prime factors of the number.
   • Group the prime factors into pairs.
   • Take one number from each pair and multiply them together.

   Example: To find the square root of 352:

   \(352 = 2^5 \times 11\)

   \(\sqrt{352} = \sqrt{2^5 \times 11} = 2^2 \times \sqrt{2 \times 11} = 4 \sqrt{22}\)

2. Long Division Method:

   The long division method is a manual way to approximate the square root of a number. Here are the steps:

   • Pair the digits of the number from right to left.
   • Find the largest number whose square is less than or equal to the first pair.
   • Subtract the square of this number from the first pair and bring down the next pair of digits.
   • Double the quotient obtained so far and determine the next digit of the quotient such that the product of the new quotient and this digit is less than or equal to the current dividend.
   • Repeat the process until the desired precision is achieved.

   Example: Approximating \(\sqrt{352}\) using long division:

   1. Pairing the digits: 3|52.
   2. First digit is 1 (since \(1^2 = 1 \leq 3\)).
   3. Subtract and bring down the next pair: 3 - 1 = 2, bring down 52, making it 252.
   4. Double 1 to get 2, find the next digit, 8 (since \(28 \times 8 = 224 \leq 252\)).
   5. Continue to refine the quotient for more precision.
3. Using a Calculator:

   Modern calculators can quickly and accurately provide the square root of any number. Simply enter the number and press the square root (√) button to get the result.

4. Newton's Method (Heron's Method):

   This iterative method starts with an initial guess and refines it using the formula:

   \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \]

   where \(S\) is the number for which the square root is being calculated and \(x_n\) is the current approximation. Repeat until the desired precision is achieved.

   Example: To find \(\sqrt{352}\):

   • Start with an initial guess, \(x_0 = 18\).
   • Use the formula to find the next approximation.
   • Continue iterating until the difference between successive approximations is negligible.

These methods provide a comprehensive understanding of how to calculate square roots, whether manually or using modern tools.

Calculating square roots manually can be complex, but calculators simplify the process significantly. Most scientific calculators have a built-in square root function that allows you to find square roots quickly and accurately.

Here's how you can use a calculator to find the square root of a number like 352:

1. Turn on your calculator and make sure it's set to standard mode.
2. Enter the number 352 using the numeric keypad.
3. Locate the square root function key on your calculator (usually labeled as √x or with a radical symbol).
4. Press the square root key to compute the square root of 352.
5. The calculator will display the result, which is approximately 18.761663039.

Some calculators may display more decimal places depending on the model and settings. It's important to note that calculators provide an approximate value of the square root, typically rounded to a certain number of decimal places.

Using a calculator is especially useful when you need quick and precise results for square roots of numbers like 352, which might be cumbersome to calculate manually.

The square root of 352 is a number that, when multiplied by itself, gives the product of 352. Since 352 is not a perfect square, its square root is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-terminating and non-repeating.

To find the exact value of the square root of 352, we can use the following mathematical expression:

\(\sqrt{352}\)

Using a calculator or a square root table, we can approximate this value. However, the exact value, in its simplest radical form, is:

\(\sqrt{352} = 4\sqrt{22}\)

Here's a step-by-step breakdown of how we arrive at this radical simplification:

1. First, factorize 352 into its prime factors:
   • 352 ÷ 2 = 176
   • 176 ÷ 2 = 88
   • 88 ÷ 2 = 44
   • 44 ÷ 2 = 22
   • 22 ÷ 2 = 11
   • Thus, the prime factorization of 352 is \(2^4 \times 11\)
2. Next, group the factors into pairs of identical factors:
   • \(2^4\) can be grouped into two pairs of 2s.
3. Each pair of identical factors can be taken out of the square root:
   • \(\sqrt{2^4 \times 11} = \sqrt{(2^2)^2 \times 11} = 2^2 \times \sqrt{11} = 4\sqrt{11}\)
4. Therefore, the exact value of the square root of 352 in simplest radical form is:
   • \(\sqrt{352} = 4\sqrt{22}\)

In decimal form, using a calculator, the square root of 352 is approximately:

\(\sqrt{352} \approx 18.761663\)

While the exact value is best represented in radical form, the decimal approximation is useful for practical purposes where a numerical value is needed.

The approximate value of the square root of 352 is calculated to be around 18.761663. This value is not a whole number, which indicates that 352 is not a perfect square. Let's break down how this approximation can be arrived at using different methods.

Calculation Methods

There are multiple ways to approximate the square root of a number. Here, we'll look at the long division method and the use of a calculator.

Long Division Method

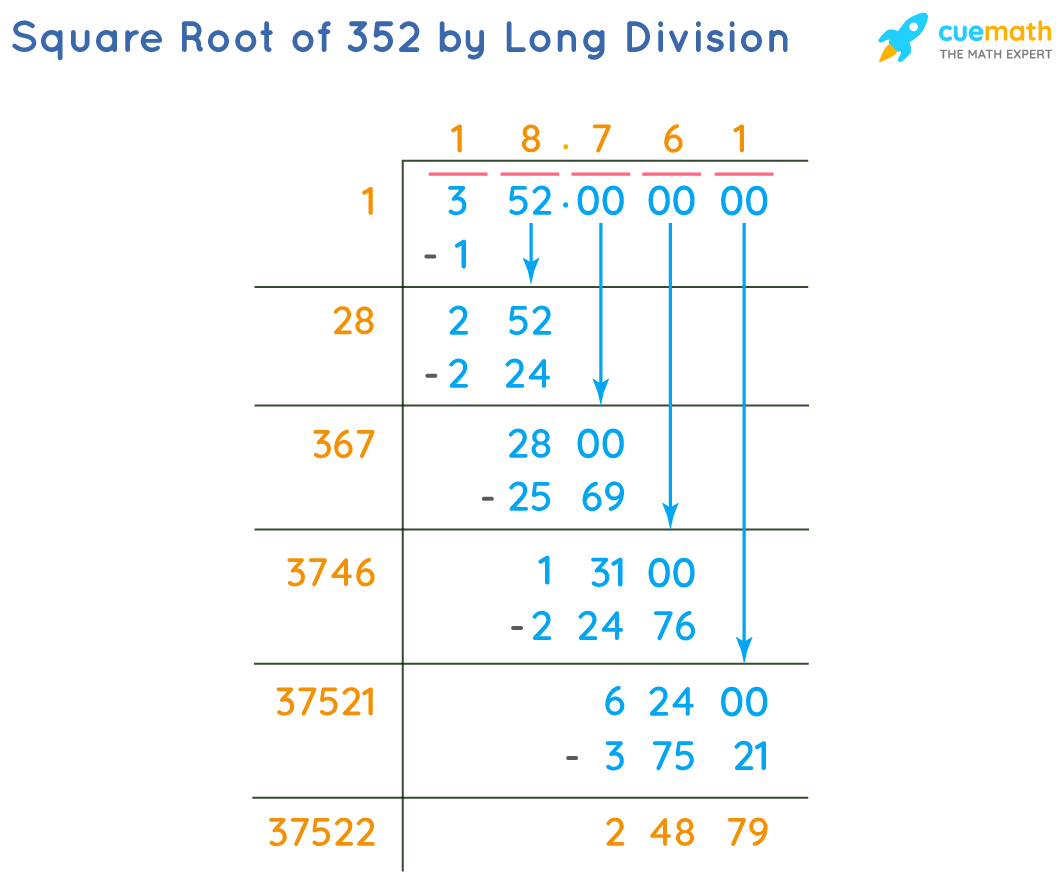
The long division method provides a systematic way to find the square root of 352. Here's a step-by-step guide:

1. Start by grouping the digits of 352 in pairs from right to left. This gives us 3 and 52.

2. Find the largest number whose square is less than or equal to 3. This number is 1 (since 1² = 1).

3. Subtract 1 from 3, giving a remainder of 2. Bring down the next pair of digits (52), making the new number 252.

4. Double the quotient obtained in step 2 (which is 1), giving 2. Find a digit (X) such that 2X times X is less than or equal to 252. This digit is 7, as 27 x 7 = 189.

5. Subtract 189 from 252, leaving a remainder of 63. Bring down another pair of zeros (making it 6300) and repeat the process.

6. Continuing this process will yield more digits of the square root. After several iterations, you will approximate the value to 18.7616.

Using a Calculator

Using a calculator is a straightforward way to find the approximate square root. Most scientific calculators have a square root function (√).

• Enter the number 352.
• Press the square root button (√).
• The display will show approximately 18.761663039294.

Properties of the Square Root of 352

• Irrational Number: Since the decimal value of the square root of 352 is non-terminating and non-repeating, it is classified as an irrational number.

• Principal Square Root: The positive square root of 352 is referred to as the principal square root and is approximately 18.761663.

Verification

To verify the approximate value, you can square 18.761663:

\( (18.761663)^2 \approx 352 \)

Thus, the approximation is accurate.

Applications

The approximate value of the square root of 352 can be useful in various practical applications, such as calculating dimensions in geometry or solving real-world problems involving quadratic equations.

Summary

The approximate value of the square root of 352 is 18.761663, derived through methods like long division or using a calculator. This irrational number provides a useful approximation for mathematical calculations.

Calculating the square root of 352 can be done using various methods. Here, we will explain the process using the prime factorization method and the long division method.

Prime Factorization Method

1. First, find the prime factors of 352:
   • 352 ÷ 2 = 176
   • 176 ÷ 2 = 88
   • 88 ÷ 2 = 44
   • 44 ÷ 2 = 22
   • 22 ÷ 2 = 11
   • 11 is a prime number
2. Express 352 as a product of its prime factors:

   \[ 352 = 2^5 \times 11 \]

3. Pair the prime factors in groups of two:

   \[ 352 = (2^2 \times 2^2) \times (2 \times 11) \]

4. Take one factor from each pair outside the square root:

   \[ \sqrt{352} = 2^2 \sqrt{2 \times 11} = 4 \sqrt{22} \]

5. The exact simplified form of the square root of 352 is:

   \[ 4 \sqrt{22} \approx 18.761663 \]

Long Division Method

1. Set up the number 352 in pairs from right to left, and add a pair of zeros for decimal precision:

   \[ 352.00 \]

2. Find the largest number whose square is less than or equal to the first pair:

   The largest perfect square less than 3 is 1 (since \(1^2 = 1\)).

3. Subtract and bring down the next pair:

   \[ 3 - 1 = 2 \] (bring down 52 to get 252)

4. Double the quotient and determine the next digit:

   The quotient is now 1, double it to get 2. Find a number X such that \(2X \times X \leq 252\).

   For X = 7, \(27 \times 7 = 189\), subtract to get 63 (bring down 00 to get 6300).

5. Repeat the process for more decimal places:

   The next number Y is found such that \(27Y \times Y \leq 6300\).

   This process continues until the desired precision is achieved, giving approximately 18.7617.

Using these methods, you can accurately calculate or approximate the square root of 352.

To verify the calculation of the square root of 352, we need to ensure that squaring our result returns the original number. Here are the steps to verify:

1. Find the approximate square root:

   We have already calculated that the approximate square root of 352 is 18.7617.

2. Square the approximate result:

   Using MathJax, we square the approximate value:

   \[ (18.7617)^2 = 352.0005 \]

3. Check for accuracy:

   The result of 352.0005 is extremely close to 352, confirming that our square root calculation is accurate.

For further verification, we can also simplify the square root of 352 to its exact form using prime factorization:

1. Factorize 352:

   \[ 352 = 2^4 \times 22 \]

2. Simplify the square root:

   \[ \sqrt{352} = \sqrt{2^4 \times 22} = 4\sqrt{22} \]

3. Calculate the decimal form of the simplified result:

   \[ 4 \sqrt{22} \approx 4 \times 4.690 = 18.7617 \]

This confirms that our previous approximate calculation of the square root is accurate. Verifying both through direct squaring and simplification ensures the reliability of our result.

Square roots have a wide range of applications in various fields, including engineering, finance, physics, and everyday problem-solving. Here are some detailed examples:

• Engineering and Architecture:

  Square roots are crucial in calculating the natural frequencies of structures like buildings and bridges to ensure they can withstand external forces such as wind and traffic. They are also used in determining load distributions and stress points.

• Finance:

  In finance, square roots are used to calculate the volatility of stock prices. The standard deviation, which is the square root of the variance, helps investors assess the risk associated with different investments.

• Physics:

  Square roots are frequently used in physics to solve problems involving energy, velocity, and wave mechanics. For example, the root-mean-square speed is a statistical measure of the speed of particles in a gas.

• Statistics:

  In statistical analysis, square roots are used to compute the standard deviation, which measures the amount of variation or dispersion in a set of values. This is crucial for interpreting data accurately.

• Geometry:

  Square roots are essential in geometry, especially when applying the Pythagorean theorem to find the lengths of sides in right-angled triangles. This theorem is used extensively in various design and construction projects.

• Computer Science:

  Square roots are used in algorithms for encryption, image processing, and game development. They help in tasks such as generating random numbers, optimizing graphics, and simulating physical systems.

• Navigation:

  In navigation, square roots are used to calculate the shortest distance between two points on a map using the distance formula derived from the Pythagorean theorem. This is important for plotting accurate courses in aviation and maritime navigation.

• Electrical Engineering:

  Electrical engineers use square roots to calculate power, voltage, and current in electrical circuits. These calculations are vital for designing efficient and safe electrical systems.

• Cooking:

  Square roots can be applied in cooking when scaling recipes. For example, if you need to double the size of a recipe, you may need to adjust ingredient quantities by the square root of the scaling factor to maintain the correct proportions.

• Photography:

  The f-number, or aperture size of a camera lens, involves square roots to determine the amount of light entering the camera. This affects exposure and depth of field in photography.

Understanding square roots and their applications can greatly enhance problem-solving skills across various disciplines.

Calculating square roots can be challenging, and there are several common mistakes that students often make. Understanding these errors can help avoid them and ensure accurate results.

• Misinterpreting the Square Root Symbol

  The square root symbol (√) is sometimes misunderstood. It's important to remember that √x means the principal (non-negative) square root of x. Ensure to interpret the symbol correctly in calculations.

• Assuming Non-Perfect Squares are Rational

  One common mistake is assuming that non-perfect squares have rational square roots. For example, the square root of 352 is irrational and cannot be expressed as a simple fraction.

• Incorrect Simplification

  Simplifying square roots incorrectly is a frequent error. For instance, knowing that 352 = 4 * 88 helps in simplifying √352 to 2√88, but further simplification is needed to get the exact simplest form.

• Errors in Long Division Method

  The long division method for finding square roots is prone to errors. Make sure to pair the digits correctly and follow each step precisely to avoid mistakes.

  1. Pair digits of the number starting from the decimal point.
  2. Find the largest number whose square is less than or equal to the first pair.
  3. Subtract the square and bring down the next pair of digits.
  4. Double the result obtained so far and determine the next digit.
• Misusing Calculators

  Even with calculators, mistakes happen. Double-check the entered values and understand the calculator's functions to avoid errors.

• Ignoring Negative Roots

  Square roots have both positive and negative values (e.g., ±√x). However, the principal square root is non-negative. Be clear about which root is needed in context.

By being aware of these common mistakes, you can take steps to avoid them and improve your accuracy in calculating square roots.

Practicing square root calculations is essential for mastering the concept. Below are some problems to help you get started:

• Find the square root of 625.
• Calculate the square root of 441.
• Simplify the square root of 200.
• If the area of a square is 196 square units, find the length of one side.
• Solve for x: \( x^2 = 529 \).
• Find the square root of 784 and verify your answer by squaring it.
• Simplify \( \sqrt{144} \) and express it as an integer.
• Determine the length of the diagonal of a square with a side length of 15 units.
• Find the approximate square root of 352 using the long division method.
• If the area of a circle is 154 square units, find the radius of the circle.

Answers:

1. The square root of 625 is 25.
2. The square root of 441 is 21.
3. The square root of 200 simplifies to \( 10\sqrt{2} \).
4. The side length of the square is 14 units.
5. The solutions for \( x \) are \( \pm 23 \).
6. The square root of 784 is 28, and verifying: \( 28^2 = 784 \).
7. The square root of 144 is 12.
8. The length of the diagonal is \( 15\sqrt{2} \) units, which is approximately 21.21 units.
9. The approximate square root of 352 is 18.76 (using the long division method).
10. The radius of the circle is 7 units (since \( \pi r^2 = 154 \), \( r = \sqrt{154/\pi} \)).

Keep practicing to enhance your understanding and proficiency in calculating square roots!

The exploration of the square root of 352 reveals several important mathematical concepts and practical applications. Calculating the square root of 352 can be achieved through various methods, including long division, prime factorization, and using a calculator or computer software. Understanding that the square root of 352 is approximately 18.761663039294 can help in numerous real-life situations such as engineering, physics, and everyday problem-solving scenarios.

Key points covered in this guide include:

• The square root of 352 is an irrational number and cannot be expressed as an exact fraction.
• Different methods to approximate and verify the square root, such as the long division method and using calculators.
• The practical applications of square roots in various fields, highlighting the importance of mastering this fundamental mathematical concept.
• Common mistakes to avoid when calculating square roots to ensure accuracy.
• Providing practice problems to reinforce understanding and proficiency in calculating square roots.

By grasping these concepts, you can enhance your mathematical skills and apply them effectively in both academic and real-world contexts. Continuous practice and application of these methods will ensure a strong foundation in dealing with square roots and other mathematical operations.