Topic square root of 332: The square root of 332 is a fundamental mathematical concept that plays a crucial role in various fields. In this article, we will explore what the square root of 332 is, how to calculate it, and its applications in real-world scenarios. Dive in to enhance your understanding of this significant mathematical value.
Table of Content
- Square Root of 332
- Introduction to the Square Root of 332
- Understanding Square Roots
- Mathematical Expression and Definition
- Decimal Approximation of the Square Root of 332
- Properties of the Square Root of 332
- Using a Calculator
- Manual Calculation Techniques
- Long Division Method
- Prime Factorization
- Applications of the Square Root of 332
- Importance in Mathematics
- Use in Science and Engineering
- Real-Life Examples
- Common Misconceptions
- Conclusion
- YOUTUBE: Tìm hiểu về căn bậc hai của 332 trong video này. Chúng tôi sẽ giải thích khái niệm và các phương pháp tính toán.
Square Root of 332
The square root of a number is a value that, when multiplied by itself, gives the original number. In this case, we are looking for the square root of 332.
Mathematical Expression
The square root of 332 can be expressed mathematically as:
\(\sqrt{332}\)
Decimal Approximation
The decimal approximation of the square root of 332 is approximately:
\(\sqrt{332} \approx 18.220867\)
Calculation Methods
- Using a calculator, simply input 332 and press the square root button.
- Using long division method, which is a manual method to find the square root of a number.
Properties of Square Root of 332
- The square root of 332 is an irrational number, meaning it cannot be expressed as a simple fraction.
- The value is non-repeating and non-terminating in its decimal form.
Applications
Understanding the square root of a number has various applications in fields such as mathematics, physics, engineering, and computer science. It is crucial for solving quadratic equations, optimizing certain calculations, and understanding geometric relationships.

READ MORE:
Introduction to the Square Root of 332
The square root of a number is a value that, when multiplied by itself, gives the original number. In this case, we are interested in the square root of 332, represented as \(\sqrt{332}\). Understanding the square root of 332 involves exploring its mathematical properties, calculating its value, and recognizing its significance in various applications.
Below is a detailed explanation of the square root of 332:
- Mathematical Definition: The square root of 332 is the number which, when squared, equals 332. Mathematically, \(\sqrt{332} \times \sqrt{332} = 332\).
- Decimal Approximation: The square root of 332 in decimal form is approximately 18.220867.
- Calculation Methods: There are various methods to calculate the square root, including using a calculator, long division, and prime factorization.
- Properties: The square root of 332 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating.
- Applications: The concept of the square root is used in many fields such as mathematics, physics, engineering, and computer science. It is crucial for solving quadratic equations, understanding geometric relationships, and more.
In the following sections, we will delve deeper into these aspects to provide a comprehensive understanding of the square root of 332.
Understanding Square Roots
Square roots are a fundamental concept in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. The symbol for the square root is \(\sqrt{}\). For example, the square root of 9 is 3, because \(3 \times 3 = 9\).
Here is a step-by-step explanation of understanding square roots:
-
Definition:
The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). This can be represented as \(y = \sqrt{x}\).
-
Properties of Square Roots:
- Every positive number has two square roots: one positive (principal square root) and one negative. For example, the square roots of 25 are 5 and -5.
- The square root of 0 is 0.
- Square roots of negative numbers are not real numbers; they are complex numbers.
-
Calculating Square Roots:
- Using a Calculator: The simplest way to find the square root of a number is by using a calculator. Enter the number and press the square root button.
- Long Division Method: This manual method involves dividing the number into pairs of digits from right to left and estimating the square root digit by digit.
- Prime Factorization: Break down the number into its prime factors and pair them to simplify the square root calculation.
-
Examples:
Let's look at some examples to illustrate:
- \(\sqrt{16} = 4\), because \(4 \times 4 = 16\).
- \(\sqrt{81} = 9\), because \(9 \times 9 = 81\).
- \(\sqrt{332} \approx 18.220867\), as 18.220867 multiplied by itself is approximately 332.
Understanding square roots is essential for solving quadratic equations, working with areas and volumes in geometry, and various applications in science and engineering. The concept extends to complex numbers and higher mathematics, making it a versatile and vital topic in mathematics.
Mathematical Expression and Definition
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, the square root of 332 can be expressed using the radical symbol as follows:
\(\sqrt{332}\)
Here is a step-by-step explanation of the mathematical expression and definition of the square root of 332:
-
Definition:
The square root of 332 is a number \(y\) such that \(y^2 = 332\). This can be written as:
\(y = \sqrt{332}\)
-
Decimal Approximation:
The square root of 332 is an irrational number, meaning it cannot be exactly expressed as a fraction. Its decimal approximation is:
\(\sqrt{332} \approx 18.220867\)
-
Properties:
- Irrational Number: The square root of 332 is an irrational number because its decimal representation is non-terminating and non-repeating.
- Non-negative Principal Root: By convention, the principal square root is the non-negative root. Thus, \(\sqrt{332} \approx 18.220867\).
- Negative Root: There is also a negative root, which is \(-\sqrt{332} \approx -18.220867\).
-
Calculation Methods:
There are various methods to calculate the square root of 332:
- Using a Calculator: The simplest method is to use a scientific calculator, input the number 332, and press the square root button.
- Long Division Method: This manual method involves a step-by-step approach to find the square root by dividing and averaging.
- Prime Factorization: Although 332 is not a perfect square, prime factorization can help understand its factors, even if it doesn't simplify the square root calculation directly.
-
Examples of Usage:
The square root function is used in various mathematical contexts, including solving quadratic equations, geometry (calculating distances), and more:
- Solving equations: If \(x^2 = 332\), then \(x = \sqrt{332}\) or \(x = -\sqrt{332}\).
- Geometry: Finding the diagonal of a square with an area of 332 square units.
Understanding the mathematical expression and definition of the square root of 332 provides a foundation for its applications in various fields of mathematics and science.
Decimal Approximation of the Square Root of 332
The square root of a number is often represented in decimal form, especially when the number is not a perfect square. In the case of 332, its square root is an irrational number, meaning it cannot be expressed exactly as a fraction and its decimal form is non-terminating and non-repeating.
Here is a detailed explanation of the decimal approximation of the square root of 332:
-
Initial Approximation:
Using a calculator or a computer, the square root of 332 can be approximated as:
\(\sqrt{332} \approx 18.220867\)
-
Step-by-Step Calculation:
To understand how this approximation is obtained, consider the following steps:
-
Estimate:
First, find the two perfect squares between which 332 lies. We know that \(18^2 = 324\) and \(19^2 = 361\). Therefore, \(\sqrt{332}\) is between 18 and 19.
-
Refine:
To get a more precise value, we use iterative methods such as the Newton-Raphson method or a calculator. For simplicity, let's use a calculator to refine the estimate.
-
Estimate:
-
Precision and Usage:
The square root of 332 is approximately 18.220867. For practical purposes, this value can be rounded to a desired level of precision depending on the context. Common approximations include:
- To two decimal places: \(\sqrt{332} \approx 18.22\)
- To three decimal places: \(\sqrt{332} \approx 18.221\)
-
Significance:
This decimal approximation is useful in various applications, such as:
- Solving real-world problems where exact values are not necessary.
- Performing calculations in engineering, physics, and computer science where a high degree of precision is required.
- Using in mathematical problems and proofs where understanding the magnitude of the square root is essential.
Understanding the decimal approximation of the square root of 332 helps in performing accurate calculations and applying this value effectively in different mathematical and scientific contexts.

Properties of the Square Root of 332
The square root of 332, represented as \(\sqrt{332}\), has several important properties that are fundamental to understanding its mathematical significance and applications. Here is a detailed exploration of these properties:
-
Irrational Number:
The square root of 332 is an irrational number. This means it cannot be expressed as a simple fraction. Its decimal representation is non-terminating and non-repeating:
\(\sqrt{332} \approx 18.220867\)
-
Non-negative Principal Root:
The principal square root of 332 is the non-negative root. Therefore:
\(\sqrt{332} \approx 18.220867\)
-
Negative Root:
There is also a negative root associated with the square root of 332:
\(-\sqrt{332} \approx -18.220867\)
-
Square Root Function:
The square root of 332 can be used in various mathematical functions and equations. It is the inverse operation of squaring a number:
If \(y = \sqrt{332}\), then \(y^2 = 332\).
-
Application in Quadratic Equations:
Understanding the square root of 332 is useful in solving quadratic equations of the form \(ax^2 + bx + c = 0\). The solutions to such equations often involve square roots.
-
Geometric Interpretation:
In geometry, the square root of a number can represent the length of the side of a square with a given area. For example, if the area of a square is 332 square units, then the length of each side is \(\sqrt{332}\) units.
-
Relationship with Other Numbers:
The square root of 332 lies between the square roots of 324 and 361, which are 18 and 19, respectively. This helps in estimating its value without precise calculation.
These properties highlight the significance of the square root of 332 in various mathematical contexts, providing a foundation for further exploration and application in more complex problems.
Using a Calculator
Calculating the square root of 332 is straightforward when using a calculator. Here is a step-by-step guide:
- Turn on your calculator and ensure it is in the standard mode (not in scientific mode, unless necessary).
- Locate the square root button. This is usually represented by the symbol √ or the letters "sqrt".
- Press the square root button (√).
- Enter the number 332.
- Press the equal sign (=) or the enter button.
The calculator will display the result, which is approximately 18.2208671582886. Here’s a breakdown of the process:
- Step 1: Ensure the calculator is on and ready.
- Step 2: Press the √ or sqrt button.
- Step 3: Input the number 332.
- Step 4: Press the equals (=) button to get the result.
This method works on most standard and scientific calculators. For more advanced calculators, you might need to use the function key (usually labeled "fn" or "shift") in conjunction with the square root button.
Using a calculator ensures that you get a precise value for the square root of 332 quickly and efficiently.
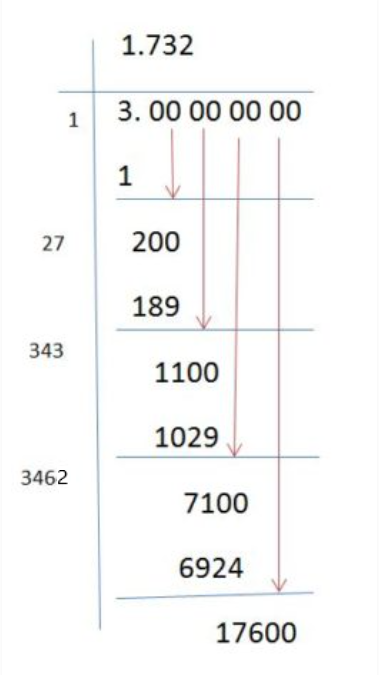
Manual Calculation Techniques
Calculating the square root of 332 manually can be done using various techniques. Here, we will discuss the long division method, which is a systematic approach for finding square roots by hand. This method involves pairing digits, estimating, and refining the root step by step.
Long Division Method
The long division method is an iterative process that allows you to find the square root of a number to a desired level of accuracy. Below are the detailed steps:
-
Pair the Digits: Separate the number into pairs of digits starting from the decimal point. For 332, we write it as
3|32|00|00...(adding pairs of zeros for precision). -
Find the Largest Integer: Find the largest integer whose square is less than or equal to the first pair (3 in this case). The largest integer is 1 because \(1^2 = 1\) and \(2^2 = 4\) (which is greater than 3).
-
Subtract and Bring Down: Subtract the square of the found integer from the first pair and bring down the next pair. Subtract \(1\) from \(3\) to get \(2\), then bring down \(32\) to make it \(232\).
-
Double the Quotient: Double the current quotient (which is 1) and place it next to the remainder (as 2_) to form a new divisor. Here, it becomes 2_.
-
Find the Next Digit: Find a digit (d) that, when placed in 2_d and multiplied by d, gives a product less than or equal to 232. The digit is 8, because \(28 \times 8 = 224\) and \(29 \times 9 = 261\) (which is greater than 232).
-
Subtract and Repeat: Subtract 224 from 232 to get 8, then bring down the next pair of zeros to make it 800. Double the current quotient (18) to get 36_, and repeat the process.
Continue this process to obtain more decimal places as required. The square root of 332 calculated manually using the long division method will be approximately 18.220867 (accurate to six decimal places).
The steps can be repeated to achieve greater precision. The manual calculation process not only helps in understanding the concept of square roots but also reinforces arithmetic skills.
Example Calculation
| Step | Action | Result |
|---|---|---|
| 1 | Initial pair: 3 | 1 (since \(1^2 = 1\)) |
| 2 | Subtract and bring down: 3 - 1 = 2, next pair 32 | 232 |
| 3 | Double quotient: 2_ | 2_ |
| 4 | Find digit: 8 (since \(28 \times 8 = 224\)) | 18 |
| 5 | Subtract and bring down: 232 - 224 = 8, next pair 00 | 800 |
| 6 | Double quotient: 36_ | 36_ |
| 7 | Find digit: 2 (since \(362 \times 2 = 724\)) | 182 |
By continuing these steps, you can get the square root of 332 to the desired level of accuracy.
Long Division Method
The long division method is a systematic way to find the square root of a number. Let's use this method to find the square root of 332.
Pair the digits of the number starting from the decimal point. For 332, we pair it as 3 | 32 | 00.
Find the largest number whose square is less than or equal to the first pair. In this case, the first pair is 3. The largest number whose square is less than or equal to 3 is 1. Write 1 above the line.
1 1 3 32 00 Square the divisor (1) and subtract it from the first pair to get the remainder. Bring down the next pair of digits (32) to the right of the remainder, making it 232.
1 1 3 32 00 1 2 32 Double the quotient (1) and write it as the new divisor with a blank digit on the right (2_).
Find a digit to fill the blank such that when this new number (2x) is multiplied by x, it gives a product less than or equal to 232. The suitable digit is 8 because 28 * 8 = 224.
18 1 3 32 00 1 2 32 2 24 Subtract 224 from 232 to get the remainder 8. Bring down the next pair of zeros to make it 800. Double the quotient (18) to get 36_.
18 1 3 32 00 1 2 32 2 24 0 80 0 Repeat the process: find a digit to fill the blank such that when 36x is multiplied by x, it gives a product less than or equal to 800. The suitable digit is 2 because 362 * 2 = 724.
18.2 1 3 32 00 1 2 32 2 24 0 80 0 7 24 Continue this process to get more decimal places if needed. The final answer is approximately 18.22.
By following these steps, you can manually calculate the square root of any number using the long division method.

Prime Factorization
The prime factorization method is an efficient way to find the square root of a number by breaking it down into its prime factors. Here is a step-by-step guide to finding the square root of 332 using the prime factorization method:
- Prime Factorization of the Number:
Start by finding the prime factors of 332. The prime factorization of 332 is:
\[332 = 2 \times 166 = 2 \times 2 \times 83\]
Therefore, the prime factors are 2, 2, and 83.
- Grouping the Prime Factors:
In this step, we group the prime factors into pairs. If a prime number appears an odd number of times, it indicates that the number is not a perfect square, and hence, we will get a decimal approximation. For 332:
\[332 = 2^2 \times 83\]
- Taking One Number from Each Pair:
For each pair of prime factors, take one number from the pair. In our case:
\[\sqrt{332} = \sqrt{2^2 \times 83} = 2\sqrt{83}\]
- Multiplying the Numbers:
Since 83 does not have a pair, it remains inside the square root. Therefore, the square root of 332 is expressed as:
\[\sqrt{332} = 2\sqrt{83}\]
Since \(\sqrt{83}\) is approximately 9.11, the square root of 332 is approximately:
\[2 \times 9.11 = 18.22\]
Thus, the square root of 332 using the prime factorization method is approximately 18.22.
Applications of the Square Root of 332
The square root of 332, approximately 18.22, has several practical applications across different fields, including mathematics, science, engineering, and daily life. Below are some detailed examples of how this square root can be applied:
1. Mathematical Applications
- Geometry: The square root of 332 can be used to determine the length of the sides of a square when the area is known. For example, if the area of a square is 332 square units, each side of the square would be approximately ≈ 18.22 units.
- Pythagorean Theorem: In right triangles, the square root of 332 can be used to find the length of a hypotenuse or a leg. If one leg is 332 units and the other leg is a known length, the hypotenuse can be found using .
2. Scientific Applications
- Physics: In physics, particularly in kinematics, the square root of 332 can be used to calculate time, distance, and velocity when dealing with equations involving square roots. For example, if an object is dropped from a height of 332 feet, the time it takes to hit the ground can be found using the formula where h is the height and g is the acceleration due to gravity.
- Engineering: In engineering, the square root of 332 can be utilized in stress analysis and structural calculations where square root values are required for determining dimensions and tolerances.
3. Real-Life Examples
- Construction: When creating square layouts or designs in construction, knowing the square root of 332 can help in accurately measuring and cutting materials.
- Accident Investigations: Investigators use square roots to calculate speeds from skid marks. For example, if skid marks are 332 feet long, the speed of the vehicle can be determined using relevant formulas involving square roots.
4. Importance in Mathematics
The square root of 332 demonstrates the significance of irrational numbers and their non-terminating, non-repeating decimal properties. This concept is crucial for understanding various mathematical theories and real-world applications that rely on precise calculations.
Overall, the square root of 332, while a simple numerical value, finds diverse applications that highlight its importance in both theoretical and practical contexts.
Importance in Mathematics
The square root of 332 holds significant importance in various mathematical contexts. Understanding its value and properties can aid in different areas of mathematics, including algebra, geometry, and number theory.
Here are some key aspects that highlight the importance of the square root of 332 in mathematics:
- Algebraic Solutions: Square roots often appear in algebraic equations and expressions. Solving equations that involve square roots is fundamental in algebra, and the square root of 332 can be part of such equations, helping to find solutions to quadratic equations.
- Geometric Interpretations: The concept of square roots is crucial in geometry, especially in calculating distances. For instance, the distance between two points in a plane can be found using the distance formula, which often involves square roots. The square root of 332 might represent a length or distance in geometric problems.
- Number Theory: In number theory, understanding the properties of square roots, including whether they are rational or irrational, helps in the study of numbers. The square root of 332 is an irrational number, which means it cannot be expressed as a simple fraction, adding to the complexity and beauty of mathematical structures.
- Pythagorean Theorem: The Pythagorean theorem frequently involves square roots when calculating the lengths of sides in right-angled triangles. The square root of 332 could be the hypotenuse or a leg length in such problems, making it a practical application of square roots in geometry.
- Simplification and Approximation: Simplifying square roots is a valuable skill in mathematics. Knowing that √332 can be simplified to 2√83 helps in performing calculations more efficiently. Additionally, approximating the value of √332, which is approximately 18.22, can be useful in real-world applications where exact values are not necessary.
Overall, the square root of 332 is a prime example of how understanding square roots is integral to various mathematical disciplines, providing a foundation for more complex mathematical concepts and real-world problem-solving.
Use in Science and Engineering
The square root of 332 has several practical applications in science and engineering. Understanding and utilizing this value can be crucial in various fields and scenarios. Here are some detailed examples of its applications:
- Physics:
In physics, the square root of 332 can be relevant when dealing with equations involving kinetic energy, wave frequencies, and other calculations where root values simplify complex numbers. For instance, certain wave equations might require the calculation of a square root to determine wavelength or frequency.
- Engineering Design:
Engineers often use square roots in design calculations. Whether it’s determining the dimensions of a structural component or the natural frequency of a system, knowing the square root of specific numbers helps in ensuring accuracy and stability in designs. For example, the resonant frequency of a mechanical system can be derived using the square root of the stiffness and mass ratio.
- Architecture:
In architecture, square roots are used to calculate areas and volumes, which are critical for designing buildings and other structures. The square root of 332 could be part of calculations involving areas of irregular shapes or optimization of space within a design.
- Electrical Engineering:
Electrical engineers use square roots in circuit analysis, especially when dealing with power calculations in AC circuits. The root mean square (RMS) value is a critical parameter in AC systems, and understanding how to compute square roots can aid in these calculations.
- Astronomy:
In astronomy, the square root function is used in various distance and velocity calculations. For instance, the square root of distances can help in estimating travel times of light or signals between celestial objects.
- Statistics:
In statistical analysis, the square root is used to compute standard deviations and variances. These are essential for understanding data distributions and variability, particularly in quality control and research experiments.
By applying the square root of 332 in these various scenarios, scientists and engineers can achieve precise and efficient results in their respective fields.

Real-Life Examples
The square root of 332, approximately 18.22, has various practical applications in real life. Here are a few examples:
- Engineering and Architecture:
Engineers and architects often use square roots when working on design calculations. For example, they may need to determine diagonal distances in structures. If a rectangular floor has an area of 332 square units, the length of each side can be calculated using the square root of 332 to ensure proper material estimation and structural integrity.
- Physics:
In physics, the square root function is frequently used to calculate quantities like standard deviation in statistical mechanics or to solve equations involving distances and speeds. For instance, if the displacement of an object is given as 332 square units in a two-dimensional plane, the direct distance from the origin can be found using the square root of 332.
- Finance:
In finance, the square root function helps in the calculation of the volatility of stock prices and other financial metrics. For example, if the variance of a financial asset's returns is 332, the standard deviation, which is the square root of the variance, gives investors an idea of the asset's risk level.
- Geography:
Geographers use square roots to determine distances between points on a map. For example, if the squared distance between two coordinates is 332 square miles, the actual distance can be found using the square root, aiding in accurate mapping and distance measurement.
- Medicine:
In medical research, the square root is used in various statistical analyses. For instance, the root mean square error (RMSE) is used to measure the differences between values predicted by a model and the values observed. If the sum of squared differences is 332, the RMSE can be calculated using the square root to provide insights into the accuracy of the model.
Common Misconceptions
Understanding the square root of a number, such as 332, can be challenging due to various common misconceptions. These misunderstandings often arise from incorrect teachings or assumptions. Here are some of the most frequent misconceptions regarding square roots:
- Square Root Always Has Two Values:
Many believe that the square root of a number always has two values, positive and negative. While it's true that the equation \( x^2 = 332 \) has two solutions, \( x = \sqrt{332} \) and \( x = -\sqrt{332} \), the principal square root function, denoted as \( \sqrt{332} \), is defined to be the non-negative value only. Therefore, \( \sqrt{332} \) refers to the positive root.
- Square Root and Squaring are Perfect Inverses:
Another misconception is that the square root function and squaring are perfect inverses of each other. For example, \( \sqrt{x^2} \) is often incorrectly thought to be \( \pm x \). In reality, \( \sqrt{x^2} \) is \( |x| \), the absolute value of \( x \), which is always non-negative. This ensures the square root function remains a well-defined function on the non-negative reals.
- Square Root of a Non-Perfect Square:
Some people think that the square root of a non-perfect square cannot be expressed meaningfully. While it is true that \( \sqrt{332} \) is not an integer, it can still be approximated to any desired level of precision, for instance, \( \sqrt{332} \approx 18.22 \). This decimal approximation is often sufficient for practical purposes.
- Square Root as a Simple Arithmetic Operation:
There is a common belief that finding the square root of a number is as straightforward as basic arithmetic operations like addition or multiplication. However, calculating square roots, especially for large or non-perfect squares like 332, often requires more advanced methods such as iterative algorithms or the use of calculators to obtain precise values.
Understanding these misconceptions is crucial for a deeper comprehension of square roots and their properties. Proper knowledge helps in applying the concept accurately in various mathematical and real-world contexts.
Conclusion
The square root of 332, approximately 18.220867, is a number that holds both mathematical and practical significance. While it is not a perfect square, making it an irrational number, understanding its value and properties is crucial in various fields such as mathematics, science, and engineering.
Mathematically, the square root of 332 can be represented as √332, and its decimal form can be derived using methods like the long division method or modern calculators. These techniques demonstrate the underlying principles of square roots and provide valuable insights into numerical computations.
Practically, the knowledge of square roots, including those of non-perfect squares like 332, is essential for solving real-world problems. For instance, it plays a role in determining dimensions in geometry, analyzing physical phenomena in science, and solving engineering challenges.
In conclusion, the exploration of the square root of 332 underscores the importance of mathematical concepts in both theoretical and applied contexts. By mastering these concepts, we can enhance our problem-solving skills and apply mathematical reasoning to a wide range of scenarios, ultimately contributing to advancements in various disciplines.
Tìm hiểu về căn bậc hai của 332 trong video này. Chúng tôi sẽ giải thích khái niệm và các phương pháp tính toán.
Căn Bậc Hai Của 332 - Hướng Dẫn Toàn Diện
READ MORE:
Khám phá căn bậc hai của 332 trong video này. Chúng tôi sẽ giải thích khái niệm và phương pháp tính toán để bạn dễ dàng hiểu.
Căn Bậc Hai Của 332 - Hướng Dẫn Toàn Diện