Topic what is the square of 6: The square of 6 is a fundamental mathematical concept with wide-ranging applications in geometry, physics, and statistics. This article will explore what the square of 6 is, how to calculate it, and its significance in various fields. Whether you're a student or a curious learner, understanding this basic calculation can be highly beneficial.
Table of Content
- Understanding the Square of 6
- Introduction to Squaring
- Mathematical Definition of Squaring
- Calculation of the Square of 6
- Properties of Squaring Numbers
- Positive and Negative Numbers
- Zero and Squaring
- Visualization of the Square of 6
- Geometric Interpretation
- Practical Applications of Squaring
- Area Calculation
- Physics and Engineering
- Statistics and Probability
- Frequently Asked Questions
- Further Reading and Resources
- YOUTUBE:
Understanding the Square of 6
In mathematics, squaring a number means multiplying the number by itself. The square of 6 can be calculated as follows:
Calculation
The square of 6 is represented mathematically as \(6^2\) or \(6 \times 6\).
Therefore, the calculation is:
- \(6 \times 6 = 36\)
Properties of Squaring
Some important properties of squaring a number include:
- The square of any positive number is always positive.
- Squaring a number greater than 1 increases its value.
- The square of 0 is 0 (\(0^2 = 0\)).
- The square of a negative number is positive (e.g., \((-6)^2 = 36\)).
Visualization
To visualize the concept, imagine a square with each side of length 6 units. The area of this square is the square of the side length:
Application in Real Life
Squaring numbers is useful in various real-life applications such as:
- Calculating area of squares and other geometric shapes.
- Physics equations involving kinetic energy (\(E_k = \frac{1}{2}mv^2\)).
- Statistical computations like variance and standard deviation.
Conclusion
Understanding the square of 6 helps in grasping basic mathematical operations and their applications. The square of 6 is:
\[
6^2 = 36
\]

READ MORE:
Introduction to Squaring
Squaring a number is a fundamental mathematical operation where a number is multiplied by itself. This operation is denoted by raising the number to the power of 2, symbolized as \( n^2 \). For example, to square the number 6, we calculate \( 6^2 \).
Here are the steps to understand squaring:
- Definition: Squaring a number means multiplying the number by itself.
- Notation: The square of a number \( n \) is written as \( n^2 \).
- Example Calculation:
- \( 6^2 = 6 \times 6 = 36 \)
- Geometric Interpretation: In geometry, the square of a number represents the area of a square with sides of that length. For instance, a square with each side measuring 6 units has an area of \( 6^2 = 36 \) square units.
Understanding the concept of squaring is essential as it forms the basis for more complex mathematical operations and has practical applications in various fields such as geometry, physics, and statistics.
Mathematical Definition of Squaring
In mathematics, squaring a number means multiplying the number by itself. The result of this operation is called the square of the number. Mathematically, this can be represented as:
\( x^2 = x \times x \)
Here, \( x \) represents the number being squared, and \( x^2 \) denotes the square of \( x \).
For example, to calculate the square of 6, we perform the following multiplication:
\( 6^2 = 6 \times 6 = 36 \)
The number 36 is the square of 6. This operation is a fundamental concept in arithmetic and algebra, with various properties and applications in different fields of mathematics and science.
- Squaring is a specific case of raising a number to a power. Specifically, it is the case where the exponent is 2.
- The square of any real number is always non-negative.
- Squaring a negative number results in a positive number, for example: \( (-6)^2 = (-6) \times (-6) = 36 \).
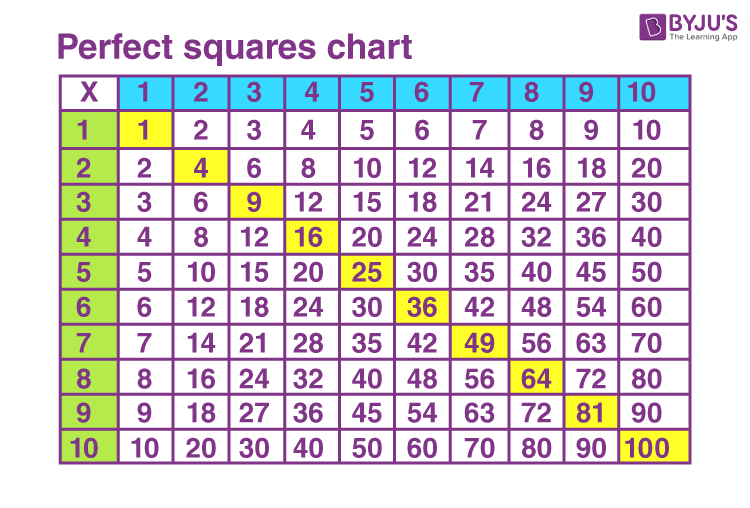
Squares of integers are also known as perfect squares. Here are some examples of perfect squares:
| Number | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
Calculation of the Square of 6
The square of a number is calculated by multiplying the number by itself. Mathematically, this is expressed as:
For the number 6, this calculation is:
Step-by-step calculation:
- Start with the number 6.
- Multiply 6 by itself:
\( 6 \times 6 \) . - The result of this multiplication is 36.
Thus, the square of 6 is:
To further understand this concept, consider the following properties of squaring numbers:
- The square of a positive number is always positive.
- The square of a negative number is also positive because a negative times a negative is positive.
- Zero squared is zero:
\( 0^2 = 0 \times 0 = 0 \) .
Additionally, the square of 6 can be visualized geometrically as the area of a square with side lengths of 6 units:
This calculation confirms that the square of 6 is 36.
Properties of Squaring Numbers
Squaring a number involves multiplying the number by itself, resulting in a value known as a square number. Here are some important properties of square numbers:
- The square of any real number is non-negative. For example, \( (-3)^2 = 9 \) and \( 3^2 = 9 \).
- Square numbers end in specific digits: 0, 1, 4, 5, 6, or 9. For instance, \(4^2 = 16\) and \(9^2 = 81\).
- If a number ends in 2, 3, 7, or 8, it is not a perfect square.
- The square of an even number is always even, and the square of an odd number is always odd.
- Perfect squares can have an even number of zeros at the end but not an odd number. For example, 100 (which is \(10^2\)) ends in two zeros.
- The unit digit of a square number is determined by the unit digit of the original number. For example, the square of a number ending in 4 ends in 6 (e.g., \(14^2 = 196\)).
- The difference between the squares of consecutive integers is always equal to the sum of the integers. For example, \((n + 1)^2 - n^2 = (n + 1) + n\).
- The sum of the first n odd numbers is always \(n^2\). For example, the sum of the first 3 odd numbers (1, 3, 5) is 9, which is \(3^2\).
- For any natural number \(n > 1\), \((2n, n^2 - 1, n^2 + 1)\) forms a Pythagorean triplet.
Understanding these properties helps in recognizing patterns in mathematics and solving various mathematical problems effectively.

Positive and Negative Numbers
The concept of squaring numbers applies to both positive and negative numbers. Here, we explore the properties and results of squaring these different types of numbers:
- Squaring Positive Numbers: When you square a positive number, the result is always positive. For example, \( 6^2 = 36 \). This is because multiplying two positive numbers together always yields a positive result.
- Squaring Negative Numbers: When you square a negative number, the result is also positive. This is due to the fact that the product of two negative numbers is positive. For instance, \( (-6)^2 = (-6) \times (-6) = 36 \).
Detailed Explanation
Let's delve into the mathematics behind these properties:
- Positive Numbers:
If \( a \) is a positive number, then squaring \( a \) is simply:
\[
a^2 = a \times a
\]Example: \( 6^2 = 6 \times 6 = 36 \)
- Negative Numbers:
If \( a \) is a negative number, say \( -a \), then squaring \( -a \) involves:
\[
(-a)^2 = (-a) \times (-a) = a^2
\]This happens because multiplying two negative numbers results in a positive number. For example:
\[
(-6)^2 = (-6) \times (-6) = 36
\]
Key Points
- The square of any real number is always non-negative.
- Squaring positive numbers results in a positive value.
- Squaring negative numbers also results in a positive value, as two negative signs cancel each other out.
Zero and Squaring
In mathematics, squaring a number means multiplying it by itself. The square of zero is a unique case with specific properties and implications.
Here are some key points about zero and squaring:
- Definition: The square of zero is calculated as \(0 \times 0 = 0\).
- Unique Property: Zero is the only number that, when squared, results in itself.
- Square Root: Zero is the only non-negative number with only one square root, which is itself. This means \( \sqrt{0} = 0 \).
- Algebraic Implications: In algebra, the property of zero is crucial. For instance, any equation of the form \(x^2 = 0\) has a unique solution \(x = 0\).
- Zero in Geometry: The concept of squaring extends to geometry, where a square with a side length of zero has an area of zero, emphasizing the point that zero squared is always zero.
Understanding the squaring of zero helps reinforce basic principles in both arithmetic and algebra, and provides a foundational concept used in more complex mathematical theories.
Visualization of the Square of 6
Visualizing the square of a number can help to understand the concept more deeply. When we square a number, we essentially create a square shape with equal side lengths. For instance, to visualize the square of 6, we can follow these steps:
- Draw a square.
- Label each side of the square with the number 6.
- Inside the square, draw a grid that divides it into smaller squares, each with side lengths of 1 unit.
- Count the number of smaller squares inside the larger square. Since each side of the square is 6 units long, the total number of smaller squares will be \(6 \times 6 = 36\).
This means that the area of the square is 36 square units, which is the same as \(6^2\).
Here’s a simple representation:
| 6 | 6 | 6 | 6 | 6 | 6 | |||||||||
This table represents a grid where each cell is 1 unit by 1 unit, and there are 36 cells in total.
Alternatively, we can use graphical tools or software to create more precise visualizations. For example, using a tool like a graphing calculator, we can plot the function \(y = x^2\) and see how it forms a parabola. For \(x = 6\), the value of \(y\) will be 36, which visually confirms the squaring process.
By visualizing the square of a number in such ways, we gain a better understanding of the geometric interpretation of squaring.
Geometric Interpretation
To understand the geometric interpretation of squaring a number, such as 6, we can visualize this process on a coordinate plane. Squaring a number is equivalent to creating a square with sides of that length.
Here’s a step-by-step breakdown:
- Basic Concept: When we square the number 6, we are essentially calculating the area of a square where each side is 6 units long.
- Calculation: The area \( A \) of the square is given by the formula: \[ A = s^2 \] where \( s \) is the side length. For \( s = 6 \): \[ A = 6^2 = 36 \]
- Visual Representation: On a graph, draw a square with each side measuring 6 units. The area inside this square represents the result of squaring 6.
To further illustrate this, consider the coordinate points:
- (0, 0)
- (6, 0)
- (6, 6)
- (0, 6)
Connecting these points forms a square. The side length is 6 units, and the enclosed area (36 square units) is the geometric representation of \( 6^2 \).
Additionally, this concept can be extended to other numbers and applied to various geometric shapes, providing a visual method to comprehend the properties of squaring in mathematics.

Practical Applications of Squaring
Squaring numbers has various practical applications across different fields. Here are some key areas where squaring is commonly used:
- Geometry: The area of a square is found by squaring the length of its sides. For example, if a square has a side length of 6 units, the area is \(6^2 = 36\) square units.
- Physics: In physics, squaring is often used to calculate quantities such as kinetic energy, which is given by the formula \(KE = \frac{1}{2}mv^2\), where \(m\) is mass and \(v\) is velocity. The squaring of velocity plays a crucial role in determining the energy.
- Statistics: Squaring is used in statistics to calculate variance, which measures how much a set of numbers is spread out. The formula for variance involves squaring the difference between each number and the mean.
- Economics: In economics, squaring is used in regression analysis to minimize the sum of the squares of the differences between observed and predicted values, a method known as least squares.
- Engineering: Engineers use squaring in various calculations, such as determining the strength of materials. For example, the moment of inertia, which is crucial for analyzing bending and torsion, is calculated by squaring the distance from the axis.
- Astronomy: In astronomy, the inverse square law states that the intensity of light or other radiation from a point source is inversely proportional to the square of the distance from the source.
- Everyday Life: Squaring is used in everyday situations, such as calculating the area of a room for flooring or painting, determining the size of a television screen (measured diagonally), and in financial calculations like compound interest.
These examples illustrate the widespread utility of squaring in practical and theoretical contexts, making it a fundamental mathematical operation with broad applications.
Area Calculation
To understand the area calculation of a square, we start with the fundamental formula for the area of a square, which is given by:
Here, represents the length of one side of the square, and is the area. For a square with a side length of 6 units, the area calculation is as follows:
This means that the area of a square with a side length of 6 units is 36 square units.
Additionally, to visualize this calculation, imagine drawing a square with each side measuring 6 units. The entire enclosed region within the square represents the area. Since area is a measure of the space inside a two-dimensional shape, the square’s area quantifies the total space within its boundaries.
To summarize:
- is the formula for the area of a square.
- For a square with side length 6 units, the area is calculated as square units.
This simple yet powerful calculation helps in various applications such as determining the space available in square plots of land, designing square-shaped objects, and more.
Physics and Engineering
The concept of squaring numbers is essential in the fields of physics and engineering. The square of 6, which is 36, finds numerous applications in these disciplines. Here, we explore several practical uses:
1. Kinematics and Dynamics
In physics, the equations of motion often involve squared terms. For instance, the equation for kinetic energy is given by:
\[ KE = \frac{1}{2}mv^2 \]
where \( m \) is mass and \( v \) is velocity. If the velocity \( v \) is 6 m/s, then:
\[ KE = \frac{1}{2}m \times 6^2 = 18m \]
This shows how squaring the velocity affects the kinetic energy.
2. Electrical Engineering
In electrical engineering, the power dissipated by a resistor is calculated using the formula:
\[ P = I^2R \]
where \( I \) is the current and \( R \) is the resistance. If the current \( I \) is 6 A, then:
\[ P = 6^2 \times R = 36R \]
This demonstrates the significance of the square of the current in determining power dissipation.
3. Structural Engineering
In structural engineering, the load-bearing capacity of beams and columns can be determined by squaring their dimensions. For example, the moment of inertia \( I \) for a rectangular beam is given by:
\[ I = \frac{1}{12}bh^3 \]
where \( b \) is the base width and \( h \) is the height. If \( h \) is 6 meters, then:
\[ I = \frac{1}{12}b \times 6^3 = \frac{1}{12}b \times 216 = 18b \]
This calculation highlights the impact of height squared on the moment of inertia.
4. Fluid Mechanics
In fluid mechanics, the Reynolds number \( Re \) is crucial for determining the flow regime of a fluid and is given by:
\[ Re = \frac{\rho v D}{\mu} \]
where \( \rho \) is the fluid density, \( v \) is the velocity, \( D \) is the characteristic length, and \( \mu \) is the dynamic viscosity. If the characteristic length \( D \) is 6 meters, then the Reynolds number scales with the square of 6:
\[ Re \propto 6^2 = 36 \]
This demonstrates how squaring the characteristic length affects the Reynolds number and, consequently, the flow behavior.
Conclusion
From these examples, it's clear that squaring numbers like 6 plays a vital role in various physics and engineering applications. Whether in energy calculations, power dissipation, structural analysis, or fluid dynamics, the square of a number helps engineers and physicists derive meaningful and practical results.
Statistics and Probability
The square of a number, such as 6, is frequently used in statistics and probability. Here, we explore its applications in various statistical measures and probability calculations.
1. Variance and Standard Deviation
Variance is a measure of the dispersion of a set of values. It is calculated by taking the average of the squared deviations from the mean. If we have a dataset where a value deviates from the mean by 6 units, the contribution to the variance is:
\[ (6 - \mu)^2 = 36 \]
Standard deviation, which is the square root of variance, also involves squaring values. The squared deviation of 6 significantly affects these measures of spread.
2. Chi-Square Tests
In probability and statistics, the chi-square test is used to determine if there is a significant association between categorical variables. The test statistic is calculated as:
\[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \]
where \( O_i \) is the observed frequency and \( E_i \) is the expected frequency. If the difference between observed and expected frequencies is 6, the contribution to the chi-square statistic is:
\[ \frac{(6)^2}{E_i} = \frac{36}{E_i} \]
This shows how the square of 6 can influence the test results.
3. Linear Regression
In linear regression, the relationship between the dependent variable and one or more independent variables is modeled. The coefficient of determination, \( R^2 \), indicates the proportion of the variance in the dependent variable that is predictable from the independent variable(s). It involves squaring the correlation coefficient \( r \):
\[ R^2 = r^2 \]
If the correlation coefficient \( r \) is 6% (or 0.06), then:
\[ R^2 = (0.06)^2 = 0.0036 \]
This illustrates the effect of squaring in determining the strength of the relationship.
4. Probability Distributions
In probability distributions, the concept of expected value often involves squaring. For instance, the variance of a probability distribution is calculated as the expected value of the squared deviation from the mean:
\[ \text{Var}(X) = E[(X - \mu)^2] \]
If the deviation is 6, the contribution to the variance is:
\[ E[(6 - \mu)^2] = 36 \]
This calculation underscores the importance of squaring in evaluating the spread of a distribution.
Conclusion
The square of 6 plays a critical role in various statistical and probability calculations. From variance and chi-square tests to linear regression and probability distributions, squaring numbers helps statisticians and analysts derive key insights and make informed decisions based on data.

Frequently Asked Questions
What is the square of 6?
The square of 6 is calculated by multiplying 6 by itself:
\[ 6 \times 6 = 36 \]
So, the square of 6 is 36.
How is the square of 6 used in mathematics?
The square of 6 is used in various mathematical contexts, including:
- Geometry: To calculate the area of a square with side length 6 units.
- Algebra: In solving quadratic equations and polynomial expressions.
- Number Theory: To explore properties of numbers and their relationships.
What are some practical applications of the square of 6?
The square of 6, which is 36, is used in many practical applications, such as:
- Physics: Calculating kinetic energy, where velocity is squared.
- Engineering: Determining structural properties and load capacities.
- Statistics: Calculating variance and standard deviation in data analysis.
Why is squaring numbers important in science and engineering?
Squaring numbers is important because it helps to quantify relationships between variables, calculate energy and power, and analyze data. It provides a way to represent and manage exponential growth, areas, and other squared quantities in scientific and engineering calculations.
Can the square of a number be negative?
No, the square of any real number is always non-negative. When you square a positive or negative number, the result is always positive. For example:
\[ 6^2 = 36 \quad \text{and} \quad (-6)^2 = 36 \]
How does the square of 6 relate to area calculations?
The square of 6 is directly related to area calculations in geometry. For example, if you have a square with each side measuring 6 units, the area \( A \) is:
\[ A = 6 \times 6 = 36 \text{ square units} \]
Is squaring the same as multiplying a number by 2?
No, squaring a number means multiplying the number by itself, while multiplying by 2 simply doubles the number. For instance:
\[ 6 \times 2 = 12 \quad \text{but} \quad 6 \times 6 = 36 \]
What is the relationship between squaring and square roots?
Squaring and square roots are inverse operations. If you square a number, you multiply it by itself. The square root of a number is a value that, when multiplied by itself, gives the original number. For example:
\[ 6^2 = 36 \quad \text{and} \quad \sqrt{36} = 6 \]
Are there any interesting properties of the number 36?
Yes, 36 has several interesting properties:
- It is a perfect square, as \( 6^2 = 36 \).
- It is a highly composite number, having more divisors than any smaller number.
- It appears in various mathematical contexts, such as the sum of a twin prime pair: \( 17 + 19 = 36 \).
Further Reading and Resources
To deepen your understanding of squaring numbers and their applications, consider exploring the following resources:
Books and Articles
- Elementary Algebra by Harold R. Jacobs
- The Art of Problem Solving: Volume 1 by Sandor Lehoczky and Richard Rusczyk
- Mathematics for the Nonmathematician by Morris Kline
This book provides a comprehensive introduction to algebraic concepts, including squaring numbers and their properties.
An excellent resource for understanding mathematical concepts and problem-solving techniques, including exercises on squaring numbers.
A great book that makes complex mathematical concepts accessible to all readers, with explanations on the importance of squaring numbers.
Online Courses
Khan Academy offers free online courses covering a wide range of mathematical topics, including arithmetic, algebra, and the concept of squaring numbers.
Coursera provides courses from top universities that delve into mathematical concepts, including algebra and geometry, where squaring numbers is extensively covered.
edX offers courses on mathematics and related fields, providing detailed explanations and practical applications of squaring numbers.
Websites and Tools
Wolfram Alpha is a computational engine that can help you understand and compute squares of numbers and their applications in various contexts.
This website offers clear explanations and interactive tools to learn about squaring numbers and other mathematical operations.
Math Planet provides free resources and exercises to help you understand algebra, geometry, and the significance of squaring numbers.
Research Papers
- The Use of Squaring in Statistical Analysis - Journal of Mathematics Education
- Applications of Squaring in Engineering - International Journal of Engineering Research
- Geometric Interpretations of Squaring - Journal of Geometry and Graphics
This paper explores how squaring is used in various statistical methods and its importance in data analysis.
A detailed study on how squaring numbers is applied in different engineering fields, enhancing structural and mechanical calculations.
An insightful paper that discusses the geometric aspects and visual representations of squaring numbers.
Videos and Tutorials
Numberphile offers engaging videos that explain mathematical concepts, including squaring numbers, in an easy-to-understand manner.
Khan Academy's YouTube channel provides video tutorials on basic and advanced mathematical topics, including the concept of squaring numbers.
TED-Ed features educational videos that cover a wide range of topics, including mathematical concepts like squaring numbers, with clear and concise explanations.
Cách Bình Phương Một Số | Bình Phương Một Số Nghĩa Là Gì? | Số Mũ | Toán Học với Mr. J
READ MORE:
Số Bình Phương Là Gì | Số Học | Toán Học | FuseSchool