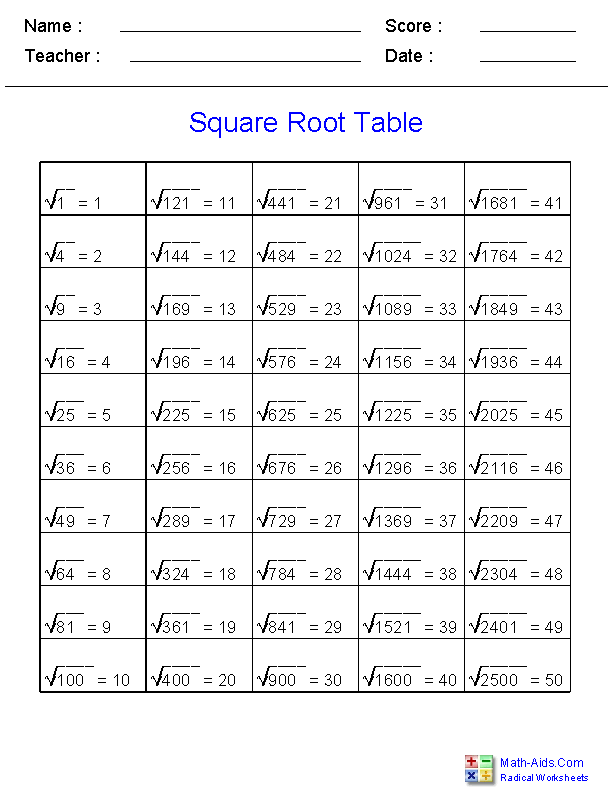
Topic square root of simplified: Simplifying square roots is a fundamental skill in algebra that helps in breaking down complex radical expressions into simpler forms. This process involves finding the prime factors and extracting perfect squares to achieve a more manageable form. Learn how to simplify square roots effectively with step-by-step examples and useful tips.
Table of Content
- Simplifying Square Roots
- Introduction
- Basic Concepts of Square Roots
- Rules for Simplifying Square Roots
- Step-by-Step Simplification Examples
- Simplifying Square Roots with Fractions
- Properties of Square Roots
- Practical Applications of Square Roots
- Advanced Topics in Square Roots
- Frequently Asked Questions
- YOUTUBE: Xem video này để học cách đơn giản hóa căn bậc hai một cách dễ dàng và hiệu quả.
Simplifying Square Roots
The process of simplifying square roots involves expressing a square root in its simplest radical form by factoring the radicand (the number inside the square root) and extracting perfect squares.
Basic Rules and Examples
To simplify a square root, follow these steps:
- Factor the radicand into its prime factors.
- Identify and extract perfect square factors.
- Multiply the extracted factors outside the square root.
For example, let's simplify the square root of 45:
\[
\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}
\]
Here, 45 is factored into 9 and 5, where 9 is a perfect square. Thus, the square root of 9 is 3, which is taken outside the square root, leaving us with \(3\sqrt{5}\).
Additional Examples
To simplify the square root of 27:
\[
\sqrt{27} = \sqrt{9 \times 3} = \sqrt{9} \times \sqrt{3} = 3\sqrt{3}
\]To simplify the square root of 8:
\[
\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2}
\]To simplify the square root of 12:
\[
\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}
\]
Applications
Simplifying square roots is useful in various mathematical calculations, including solving quadratic equations, simplifying expressions, and calculating areas and lengths in geometry.
Using Square Root Calculators
Online square root calculators can help simplify square roots quickly and accurately. Some useful calculators include:
Conclusion
Understanding how to simplify square roots is fundamental in mathematics. It aids in making complex calculations more manageable and provides a foundation for more advanced mathematical concepts.

READ MORE:
Introduction
The concept of simplifying square roots is essential in various mathematical contexts. Simplification involves expressing a square root in its simplest radical form. This process requires understanding the properties of square roots and factoring numbers to identify perfect square factors. Through simplification, complex square roots become easier to work with, which is particularly useful in algebra, geometry, and other mathematical applications.
Basic Concepts of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, this is represented as:
\(\sqrt{x} = y\) such that \(y^2 = x\).
Square roots are often simplified to make them easier to work with. Simplifying a square root involves factoring the number inside the square root (the radicand) into its prime factors and pulling out pairs of prime factors.
Let's break down the process:
- Find the prime factorization of the radicand.
- Group the factors into pairs of identical factors.
- Move one factor from each pair outside the square root.
For example, to simplify \(\sqrt{18}\):
- Find the prime factors of 18: \(18 = 2 \times 3^2\).
- Identify pairs of prime factors: \(3^2\) is a pair.
- Move the paired factor outside the square root: \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\).
This process shows that \(\sqrt{18}\) simplifies to \(3\sqrt{2}\).
Other examples include:
- \(\sqrt{45} = \sqrt{9 \times 5} = 3\sqrt{5}\)
- \(\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}\)
Simplifying square roots makes it easier to work with radical expressions, especially when performing operations like addition, subtraction, or comparison of square roots.
Rules for Simplifying Square Roots
Understanding the rules for simplifying square roots is essential for solving mathematical problems efficiently. Here, we outline the key steps and concepts involved in this process:
- Identify Perfect Squares: Find the largest perfect square factor of the radicand (the number under the square root). For example, in √18, the largest perfect square factor is 9.
- Use the Product Rule: Apply the rule √(a × b) = √a × √b to break down the radicand. For √18, we can write it as √(9 × 2).
- Simplify the Square Root: Take the square root of the perfect square. Since √9 is 3, we get 3√2 for √18.
- Prime Factorization: For more complex numbers, factorize the radicand into its prime factors and group them into pairs. For instance, √72 can be factorized into √(2×2×2×3×3), which simplifies to 6√2.
- Combining Square Roots: If you have multiple square roots multiplied together, combine them into one root and simplify. For example, √8 × √2 = √(8×2) = √16 = 4.
- Dealing with Fractions: Simplify square roots in fractions by applying the rule √(a/b) = √a / √b. For instance, √(4/9) simplifies to 2/3.
- Addition and Subtraction: Combine like terms under the same root. For example, 2√3 + 3√3 = 5√3.
These rules help in making square roots simpler and easier to handle in various mathematical contexts.
Step-by-Step Simplification Examples
Understanding how to simplify square roots involves breaking down the number under the square root into its prime factors. Here are detailed examples to guide you through the process:
-
Example 1: Simplify \(\sqrt{12}\)
- Identify the factors of 12: \(12 = 4 \times 3\)
- Use the square root rule: \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\)
- Apply the rule: \(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3}\)
- Simplify the square roots: \(\sqrt{4} = 2\)
- Thus, \(\sqrt{12} = 2\sqrt{3}\)
-
Example 2: Simplify \(\sqrt{45}\)
- Identify the factors of 45: \(45 = 9 \times 5\)
- Apply the square root rule: \(\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5}\)
- Simplify the square roots: \(\sqrt{9} = 3\)
- Thus, \(\sqrt{45} = 3\sqrt{5}\)
-
Example 3: Simplify \(\sqrt{108}\)
- Identify the factors of 108: \(108 = 36 \times 3\)
- Apply the square root rule: \(\sqrt{108} = \sqrt{36 \times 3} = \sqrt{36} \times \sqrt{3}\)
- Simplify the square roots: \(\sqrt{36} = 6\)
- Thus, \(\sqrt{108} = 6\sqrt{3}\)
-
Example 4: Simplify \(\sqrt{8}\)
- Identify the factors of 8: \(8 = 4 \times 2\)
- Apply the square root rule: \(\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2}\)
- Simplify the square roots: \(\sqrt{4} = 2\)
- Thus, \(\sqrt{8} = 2\sqrt{2}\)
These examples illustrate how to simplify square roots by factoring the number under the radical and using the property of square roots to break it down into simpler parts. Practice with different numbers to become more familiar with the process.
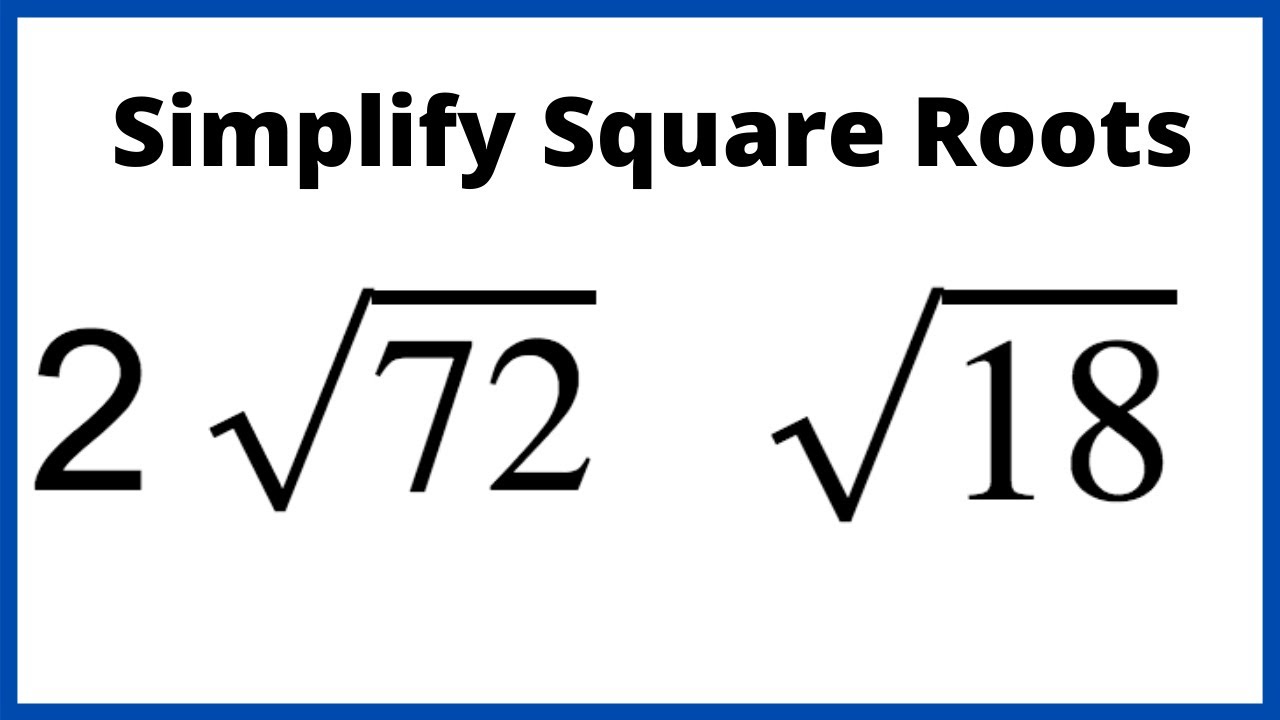
Simplifying Square Roots with Fractions
Simplifying square roots that involve fractions can be approached in a structured manner. Follow these steps to simplify such expressions:
- Identify the square root:
Start with the fraction under the square root, for example, \( \sqrt{\frac{a}{b}} \).
- Separate the fraction:
Use the property of square roots to separate the numerator and the denominator:
\( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). - Simplify the numerator and the denominator:
Simplify \( \sqrt{a} \) and \( \sqrt{b} \) individually if possible.
- Rationalize the denominator (if needed):
If the denominator contains a square root, rationalize it by multiplying the numerator and denominator by the square root in the denominator. For example, \( \frac{a}{\sqrt{b}} \) becomes \( \frac{a\sqrt{b}}{b} \).
Let's look at a detailed example to illustrate these steps:
Example: Simplify \( \sqrt{\frac{8}{2}} \).
- Identify the square root: \( \sqrt{\frac{8}{2}} \).
- Separate the fraction: \( \frac{\sqrt{8}}{\sqrt{2}} \).
- Simplify the numerator and the denominator:
- \( \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} \).
- \( \sqrt{2} \) remains as it is.
- Form the fraction with simplified terms: \( \frac{2\sqrt{2}}{\sqrt{2}} \).
- Simplify further by canceling out \( \sqrt{2} \): \( 2 \).
Thus, \( \sqrt{\frac{8}{2}} = 2 \).
This method can be applied to any fraction under a square root, ensuring that the expression is simplified in a step-by-step manner.
Properties of Square Roots
The properties of square roots are essential for simplifying and understanding how they work in different mathematical contexts. Here are some key properties:
- Product Property: The square root of a product is equal to the product of the square roots of each factor.
\(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\)
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator.
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Perfect Squares: The square root of a perfect square is always an integer.
\(\sqrt{n^2} = n\)
- Non-Negativity: The square root of a non-negative number is always non-negative.
\(\sqrt{a} \geq 0 \quad \text{for all} \quad a \geq 0\)
- Addition and Subtraction: Square roots cannot be directly added or subtracted unless they are like terms.
\(\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}\)
- Distributive Property: Square roots distribute over multiplication and division but not over addition and subtraction.
\(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Simplifying Square Roots: To simplify a square root, factor the number inside the radical to its prime factors and pair the factors.
Example: \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)
Practical Applications of Square Roots
Square roots have numerous practical applications in various fields. Here are some common uses:
- Finance: Square roots are used to calculate stock market volatility. For example, the volatility of a stock’s returns is determined by taking the square root of the variance of those returns.
- Architecture: Engineers use square roots to determine the natural frequencies of structures like bridges and buildings, which helps in predicting how they will respond to various loads.
- Science: In physics, square roots are used to calculate velocities, intensities of sound waves, and radiation levels. For example, the time it takes for an object to fall from a certain height is determined using the square root of the height.
- Statistics: Square roots are essential in calculating standard deviation and variance, which measure the spread of data points in a data set.
- Geometry: Square roots are used to determine the lengths of sides in right triangles via the Pythagorean theorem, and to calculate areas and perimeters of various geometric shapes.
- Computer Science: Square roots are used in algorithms for encryption, image processing, and game physics, such as calculating distances between points or lengths of vectors.
- Cryptography: Square roots are crucial in generating digital signatures and secure communication channels, leveraging properties of prime numbers and modular arithmetic.
- Navigation: Square roots help in calculating distances between geographical points and determining the most efficient routes for navigation.
- Electrical Engineering: Engineers use square roots to compute power, voltage, and current in circuits, and to design filters and signal-processing devices.
- Cooking: Scaling recipes often involves adjusting quantities proportionally, which can involve square roots to maintain the correct balance of flavors.
- Photography: The aperture of a camera lens is related to the f-number, which involves square roots. Changing the f-number by a factor of two affects the amount of light by a factor of four.
- Computer Graphics: Square roots are used to calculate distances and render images accurately in both 2D and 3D environments.
- Telecommunication: Signal strength in wireless communication diminishes with the square of the distance from the transmitter, known as the inverse square law.
Advanced Topics in Square Roots
Advanced topics in square roots delve into more complex concepts that extend beyond basic simplification and calculation. These topics are crucial for higher-level mathematics, including algebra, calculus, and complex number theory.
- Square Roots of Negative Numbers
The square root of a negative number introduces the concept of imaginary numbers. The imaginary unit, denoted as \(i\), is defined by the property \(i^2 = -1\). For any negative number \(-a\), its square root can be expressed as \(\sqrt{-a} = i\sqrt{a}\).
Example: \(\sqrt{-16} = 4i\)
- Complex Numbers and Their Square Roots
Complex numbers are of the form \(a + bi\), where \(a\) and \(b\) are real numbers, and \(i\) is the imaginary unit. Finding the square root of a complex number involves converting it to polar form and using De Moivre's Theorem.
Example: To find the square root of \(3 + 4i\), convert it to polar form and apply the theorem.
- Square Roots in Algebraic Equations
Square roots frequently appear in algebraic equations, particularly in solving quadratic equations. The quadratic formula \(\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) involves the square root of the discriminant.
Example: Solve \(x^2 + 6x + 9 = 0\) using the quadratic formula.
- Properties of Radicals and Exponents
Understanding the properties of radicals is essential for manipulating expressions involving square roots. Key properties include the product rule \(\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}\) and the quotient rule \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\).
Example: Simplify \(\sqrt{50} \cdot \sqrt{2} = \sqrt{100} = 10\).
- Applications in Higher Mathematics
Square roots play a significant role in higher mathematics, including calculus and linear algebra. In calculus, they are used in limit processes and defining derivatives and integrals involving radical functions. In linear algebra, they are used in matrix operations and determining eigenvalues.
Example: In calculus, find the derivative of \(f(x) = \sqrt{x^2 + 1}\).

Frequently Asked Questions
- What is the square root of a simplified expression?
- How do I find the square root of a simplified expression?
- Can square roots of simplified expressions be simplified further?
- What are some common mistakes to avoid when simplifying square roots?
- Are there any shortcuts or tricks for simplifying square roots?
The square root of a simplified expression is the number which, when multiplied by itself, equals the simplified expression. For example, if we have the simplified expression √9, the square root is 3 because 3 × 3 = 9.
To find the square root of a simplified expression, you can first factor the expression into its prime factors and then take the square root of each factor. Finally, multiply together any identical factors that appear in pairs. For instance, to find the square root of √12, you can factor it as √(2 × 2 × 3) = 2√3.
Yes, in many cases, square roots of simplified expressions can be simplified further by identifying perfect square factors. For example, the expression √12 can be simplified to 2√3 because 12 can be factored into 2 × 2 × 3, and 2 × 2 = 4, which is a perfect square.
One common mistake is forgetting to identify perfect square factors within the expression. Another mistake is incorrectly multiplying or combining terms. It's essential to carefully follow the rules of simplification to avoid errors.
While there are no universal shortcuts, becoming familiar with common perfect squares and prime factorization techniques can help streamline the simplification process. Additionally, practicing regularly can improve your speed and accuracy in simplifying square roots.
Xem video này để học cách đơn giản hóa căn bậc hai một cách dễ dàng và hiệu quả.
Hướng Dẫn Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Xem video này để học cách đơn giản hóa căn bậc hai với Thầy J.
Đơn Giản Hóa Căn Bậc Hai | Toán với Thầy J