Topic simplifying square roots: Welcome to our guide on simplifying square roots. In this article, we will explore the essential concepts, rules, and techniques needed to master this fundamental mathematical skill. Whether you're a student or just looking to refresh your knowledge, this comprehensive guide will provide you with the tools and confidence to simplify square roots with ease.
Table of Content
- Simplifying Square Roots
- Introduction to Simplifying Square Roots
- Basic Concepts and Rules
- Step-by-Step Simplification Process
- Examples and Practice Problems
- Advanced Techniques
- Applications and Real-World Uses
- YOUTUBE: Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai để giúp bạn nắm vững các khái niệm và áp dụng vào các bài toán thực tế.
Simplifying Square Roots
Simplifying square roots involves reducing the expression under the square root to its simplest form. This process often uses the properties of square roots and prime factorization. Below are various methods and examples to understand the simplification process better.
Basic Method
- Factor the number inside the square root into its prime factors.
- Group the factors into pairs of the same number.
- Take one number out of the square root for every pair of factors.
- Multiply the numbers taken out of the square root.
Examples
-
Example 1: Simplify \( \sqrt{12} \)
Step 1: Factor 12 into prime factors: \( 12 = 2 \times 2 \times 3 \)
Step 2: Group the factors: \( \sqrt{12} = \sqrt{2^2 \times 3} \)
Step 3: Take one number out for each pair: \( \sqrt{12} = 2\sqrt{3} \)
-
Example 2: Simplify \( \sqrt{45} \)
Step 1: Factor 45 into prime factors: \( 45 = 3 \times 3 \times 5 \)
Step 2: Group the factors: \( \sqrt{45} = \sqrt{3^2 \times 5} \)
Step 3: Take one number out for each pair: \( \sqrt{45} = 3\sqrt{5} \)
Using the Product Rule
The product rule states that \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). This rule is useful when simplifying square roots involving products.
-
Example 3: Simplify \( \sqrt{20 \cdot 5} \)
Step 1: Combine under one square root: \( \sqrt{20 \cdot 5} = \sqrt{100} \)
Step 2: Simplify: \( \sqrt{100} = 10 \)
Using the Quotient Rule
The quotient rule states that \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). This rule helps simplify square roots involving fractions.
-
Example 4: Simplify \( \sqrt{\frac{25}{9}} \)
Step 1: Apply the quotient rule: \( \sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}} \)
Step 2: Simplify: \( \frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3} \)
Complex Examples
-
Example 5: Simplify \( 2\sqrt{12} + 9\sqrt{3} \)
Step 1: Simplify \( 2\sqrt{12} \): \( 2 \times 2\sqrt{3} = 4\sqrt{3} \)
Step 2: Combine like terms: \( 4\sqrt{3} + 9\sqrt{3} = 13\sqrt{3} \)
Prime Factorization Method
This method involves breaking down the number inside the square root into its prime factors and then simplifying.
-
Example 6: Simplify \( \sqrt{90} \)
Step 1: Factor 90 into primes: \( 90 = 2 \times 3 \times 3 \times 5 \)
Step 2: Group factors: \( \sqrt{90} = \sqrt{3^2 \times 2 \times 5} \)
Step 3: Simplify: \( \sqrt{90} = 3\sqrt{10} \)
Simplifying Fractions
-
Example 7: Simplify \( \frac{\sqrt{32}}{\sqrt{2}} \)
Step 1: Combine under one square root: \( \frac{\sqrt{32}}{\sqrt{2}} = \sqrt{\frac{32}{2}} \)
Step 2: Simplify: \( \sqrt{16} = 4 \)
By understanding these methods, simplifying square roots becomes a straightforward process that can be applied to various mathematical problems.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is an essential skill in mathematics that helps to make expressions involving radicals more manageable. A square root is a value that, when multiplied by itself, gives the original number. For instance, the square root of 25 is 5, because \(5 \times 5 = 25\). In this section, we will explore the basic concepts and rules for simplifying square roots, including perfect squares, prime factorization, and the properties of radicals.
To simplify a square root, follow these steps:
- Identify and factor out perfect squares from the number under the square root.
- Rewrite the square root as the product of the square roots of the factors.
- Simplify the square roots of the perfect square factors.
For example, to simplify \(\sqrt{72}\):
- Factor 72 into \(36 \times 2\) (since 36 is a perfect square).
- Rewrite \(\sqrt{72}\) as \(\sqrt{36 \times 2}\).
- Use the property of radicals: \(\sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2}\).
- Simplify \(\sqrt{36}\) to 6, resulting in \(6 \sqrt{2}\).
Thus, \(\sqrt{72} = 6 \sqrt{2}\).
Understanding these steps and practicing with various examples will enhance your ability to simplify square roots efficiently.
Basic Concepts and Rules
Understanding the basic concepts and rules of square roots is crucial for simplifying them effectively. Below are the key concepts and rules to keep in mind:
Definition of Square Roots
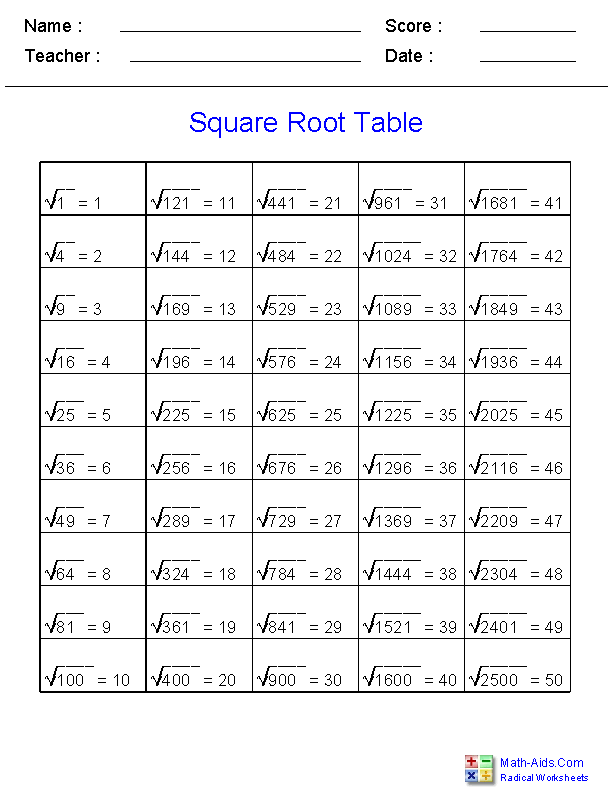
A square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). For example, the square root of 16 is 4 because \(4^2 = 16\). The square root symbol is denoted as \(\sqrt{}\).
Perfect Squares
Perfect squares are numbers that are the square of integers. Examples include:
- \(1 = 1^2\)
- \(4 = 2^2\)
- \(9 = 3^2\)
- \(16 = 4^2\)
- \(25 = 5^2\)
Product Rule for Radicals
The product rule for radicals states that the square root of a product is equal to the product of the square roots of the factors:
\[
\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}
\]
For example, \(\sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6 \sqrt{2}\).
Quotient Rule for Radicals
The quotient rule for radicals states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
For example, \(\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2}\).
Prime Factorization Method
Prime factorization involves breaking down a number into its prime factors and then simplifying the square root by pairing identical factors:
- Find the prime factorization of the number.
- Group the prime factors into pairs.
- Move one factor from each pair outside the square root.
For example, to simplify \(\sqrt{72}\):
- Prime factorize 72: \(72 = 2 \times 2 \times 2 \times 3 \times 3\).
- Group the factors: \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = \sqrt{4 \times 9 \times 2}\).
- Simplify: \(\sqrt{4 \times 9 \times 2} = 2 \times 3 \times \sqrt{2} = 6 \sqrt{2}\).
These basic concepts and rules are fundamental for simplifying square roots efficiently and accurately.
Step-by-Step Simplification Process
Simplifying square roots involves a systematic approach to breaking down the number under the radical sign. Follow these steps to simplify square roots effectively:
- Prime Factorization
Start by finding the prime factorization of the number under the square root. Prime factorization involves breaking down a number into its prime factors, which are numbers that can only be divided by 1 and themselves.
- Example: To simplify \(\sqrt{72}\), first find the prime factors of 72. The prime factorization of 72 is \(2 \times 2 \times 2 \times 3 \times 3\).
- Group the Prime Factors
Group the prime factors into pairs. Each pair of identical factors will be simplified outside the square root.
- Example: Group the prime factors of 72 as \( (2 \times 2) \times (3 \times 3) \times 2 \).
- Move Pairs Outside the Radical
For each pair of prime factors, move one factor outside the radical sign.
- Example: Simplify \(\sqrt{(2 \times 2) \times (3 \times 3) \times 2}\) to \(2 \times 3 \times \sqrt{2} = 6 \sqrt{2}\).
- Simplify the Expression
Combine the factors outside the radical to get the simplified form of the square root.
- Example: The simplified form of \(\sqrt{72}\) is \(6 \sqrt{2}\).
Let's look at another example:
To simplify \(\sqrt{200}\):
- Prime factorize 200: \(200 = 2 \times 2 \times 2 \times 5 \times 5\).
- Group the factors: \( \sqrt{200} = \sqrt{(2 \times 2) \times (5 \times 5) \times 2} = \sqrt{4 \times 25 \times 2}\).
- Move pairs outside the radical: \(\sqrt{4 \times 25 \times 2} = 2 \times 5 \times \sqrt{2} = 10 \sqrt{2}\).
- The simplified form of \(\sqrt{200}\) is \(10 \sqrt{2}\).
By following these steps and practicing with different numbers, you will become proficient at simplifying square roots.
Examples and Practice Problems
Understanding the theory behind simplifying square roots is essential, but practice is key to mastery. Below are examples and practice problems to help you apply the concepts and techniques discussed.
Simple Examples
- Simplify \(\sqrt{50}\):
- Prime factorize 50: \(50 = 2 \times 5 \times 5\).
- Group the factors: \(\sqrt{50} = \sqrt{2 \times (5 \times 5)} = \sqrt{2 \times 25}\).
- Move pairs outside the radical: \(\sqrt{2 \times 25} = 5 \sqrt{2}\).
So, \(\sqrt{50} = 5 \sqrt{2}\).
- Simplify \(\sqrt{18}\):
- Prime factorize 18: \(18 = 2 \times 3 \times 3\).
- Group the factors: \(\sqrt{18} = \sqrt{2 \times (3 \times 3)} = \sqrt{2 \times 9}\).
- Move pairs outside the radical: \(\sqrt{2 \times 9} = 3 \sqrt{2}\).
So, \(\sqrt{18} = 3 \sqrt{2}\).
Complex Examples
- Simplify \(\sqrt{128}\):
- Prime factorize 128: \(128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2\).
- Group the factors: \(\sqrt{128} = \sqrt{(2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2} = \sqrt{4 \times 4 \times 4 \times 2}\).
- Move pairs outside the radical: \(\sqrt{4 \times 4 \times 4 \times 2} = 2 \times 2 \times 2 \times \sqrt{2} = 8 \sqrt{2}\).
So, \(\sqrt{128} = 8 \sqrt{2}\).
- Simplify \(\sqrt{252}\):
- Prime factorize 252: \(252 = 2 \times 2 \times 3 \times 3 \times 7\).
- Group the factors: \(\sqrt{252} = \sqrt{(2 \times 2) \times (3 \times 3) \times 7} = \sqrt{4 \times 9 \times 7}\).
- Move pairs outside the radical: \(\sqrt{4 \times 9 \times 7} = 2 \times 3 \times \sqrt{7} = 6 \sqrt{7}\).
So, \(\sqrt{252} = 6 \sqrt{7}\).
Mixed Radicals
- Simplify \(3 \sqrt{8} + 2 \sqrt{18}\):
- Simplify each term separately: \(3 \sqrt{8} = 3 \times 2 \sqrt{2} = 6 \sqrt{2}\) and \(2 \sqrt{18} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}\).
- Combine like terms: \(6 \sqrt{2} + 6 \sqrt{2} = 12 \sqrt{2}\).
So, \(3 \sqrt{8} + 2 \sqrt{18} = 12 \sqrt{2}\).
- Simplify \(5 \sqrt{12} - \sqrt{75}\):
- Simplify each term separately: \(5 \sqrt{12} = 5 \times 2 \sqrt{3} = 10 \sqrt{3}\) and \(\sqrt{75} = 5 \sqrt{3}\).
- Combine like terms: \(10 \sqrt{3} - 5 \sqrt{3} = 5 \sqrt{3}\).
So, \(5 \sqrt{12} - \sqrt{75} = 5 \sqrt{3}\).
Fractions and Square Roots
- Simplify \(\sqrt{\frac{49}{16}}\):
- Apply the quotient rule: \(\sqrt{\frac{49}{16}} = \frac{\sqrt{49}}{\sqrt{16}} = \frac{7}{4}\).
So, \(\sqrt{\frac{49}{16}} = \frac{7}{4}\).
- Simplify \(\sqrt{\frac{75}{8}}\):
- Prime factorize the numerator and denominator: \(\sqrt{\frac{75}{8}} = \sqrt{\frac{3 \times 5 \times 5}{2 \times 2 \times 2}}\).
- Simplify inside the radical: \(\sqrt{\frac{75}{8}} = \frac{5 \sqrt{3}}{2 \sqrt{2}}\).
- Rationalize the denominator: \(\frac{5 \sqrt{3}}{2 \sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{5 \sqrt{6}}{4}\).
So, \(\sqrt{\frac{75}{8}} = \frac{5 \sqrt{6}}{4}\).
Practice these examples and problems to enhance your understanding and proficiency in simplifying square roots.
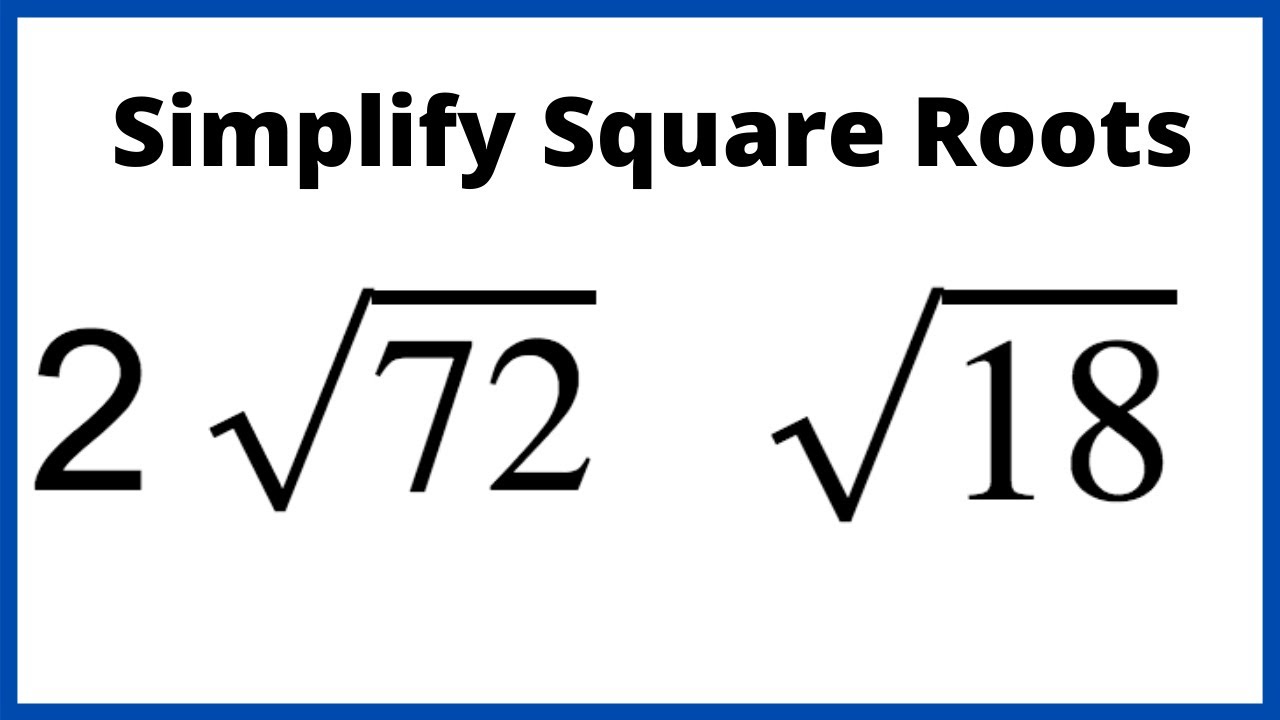
Advanced Techniques
Once you have mastered the basics of simplifying square roots, you can move on to more advanced techniques. These methods will help you tackle more complex problems involving radicals.
Simplifying Non-Numerical Radicals
When simplifying radicals involving variables, the same principles apply as with numerical radicals. Ensure that the variable is part of a perfect square before simplifying.
- Simplify \(\sqrt{50x^2}\):
- Factor 50 into \(25 \times 2\), and note that \(x^2\) is a perfect square.
- Rewrite the expression: \(\sqrt{50x^2} = \sqrt{25 \times 2 \times x^2}\).
- Simplify: \(\sqrt{25} \times \sqrt{2} \times \sqrt{x^2} = 5x \sqrt{2}\).
So, \(\sqrt{50x^2} = 5x \sqrt{2}\).
- Simplify \(\sqrt{72y^4}\):
- Factor 72 into \(36 \times 2\), and note that \(y^4\) is a perfect square.
- Rewrite the expression: \(\sqrt{72y^4} = \sqrt{36 \times 2 \times y^4}\).
- Simplify: \(\sqrt{36} \times \sqrt{2} \times \sqrt{y^4} = 6y^2 \sqrt{2}\).
So, \(\sqrt{72y^4} = 6y^2 \sqrt{2}\).
Using the Quotient Property
The quotient property of square roots allows you to simplify expressions involving division within a radical.
- Simplify \(\sqrt{\frac{45}{5}}\):
- Divide the numbers inside the radical: \(\frac{45}{5} = 9\).
- Take the square root: \(\sqrt{9} = 3\).
So, \(\sqrt{\frac{45}{5}} = 3\).
- Simplify \(\sqrt{\frac{98}{2}}\):
- Divide the numbers inside the radical: \(\frac{98}{2} = 49\).
- Take the square root: \(\sqrt{49} = 7\).
So, \(\sqrt{\frac{98}{2}} = 7\).
Dealing with Variables in Radicals
When dealing with variables under the radical sign, the goal is to simplify them as much as possible, just like numerical radicals. Assume all variables represent non-negative values to avoid dealing with complex numbers.
- Simplify \(\sqrt{32x^6}\):
- Prime factorize 32: \(32 = 2 \times 2 \times 2 \times 2 \times 2 = 2^5\).
- Rewrite the expression: \(\sqrt{32x^6} = \sqrt{2^5 \times x^6}\).
- Group the factors: \(\sqrt{2^4 \times 2 \times x^6} = \sqrt{(2^2)^2 \times 2 \times (x^3)^2}\).
- Simplify: \(2^2 \times x^3 \times \sqrt{2} = 4x^3 \sqrt{2}\).
So, \(\sqrt{32x^6} = 4x^3 \sqrt{2}\).
- Simplify \(\sqrt{50y^3}\):
- Prime factorize 50: \(50 = 2 \times 5^2\).
- Rewrite the expression: \(\sqrt{50y^3} = \sqrt{2 \times 5^2 \times y^3}\).
- Group the factors: \(\sqrt{(5)^2 \times 2 \times y^2 \times y}\).
- Simplify: \(5y \sqrt{2y}\).
So, \(\sqrt{50y^3} = 5y \sqrt{2y}\).
Practicing these advanced techniques will improve your ability to simplify any square root expression you encounter.
Applications and Real-World Uses
Simplifying square roots is not just an academic exercise; it has numerous practical applications in various fields. Understanding how to simplify square roots can help in solving real-world problems efficiently and accurately.
Geometry and Measurements
In geometry, simplifying square roots is essential for calculating distances, areas, and volumes, especially when dealing with right triangles and circles.
- Pythagorean Theorem:
To find the length of the hypotenuse in a right triangle, you use the Pythagorean theorem: \(c = \sqrt{a^2 + b^2}\).
- Example: If \(a = 3\) and \(b = 4\), then \(c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\).
- Circle Measurements:
To find the radius or diameter from the area of a circle, you use the formula \(A = \pi r^2\). Solving for \(r\), we get \(r = \sqrt{\frac{A}{\pi}}\).
- Example: If the area \(A = 50\pi\), then \(r = \sqrt{\frac{50\pi}{\pi}} = \sqrt{50} \approx 7.07\).
Physics and Engineering
Simplifying square roots is crucial in physics and engineering for solving equations involving energy, forces, and waves.
- Kinetic Energy:
The kinetic energy (\(KE\)) of an object is given by \(KE = \frac{1}{2}mv^2\). To find the velocity (\(v\)), you can solve for \(v\): \(v = \sqrt{\frac{2KE}{m}}\).
- Example: If \(KE = 200\) joules and \(m = 5\) kg, then \(v = \sqrt{\frac{2 \times 200}{5}} = \sqrt{80} \approx 8.94\) m/s.
- Wave Speed:
The speed (\(v\)) of a wave is given by \(v = \sqrt{\frac{T}{\mu}}\), where \(T\) is the tension and \(\mu\) is the linear density.
- Example: If \(T = 100\) N and \(\mu = 0.01\) kg/m, then \(v = \sqrt{\frac{100}{0.01}} = \sqrt{10000} = 100\) m/s.
Finance and Economics
Square roots are also used in finance and economics, particularly in calculations involving interest rates and economic models.
- Standard Deviation:
In statistics, the standard deviation (\(\sigma\)) measures the amount of variation or dispersion in a set of values. It is given by \(\sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}}\).
- Example: If the variance of a dataset is 25, then the standard deviation is \(\sigma = \sqrt{25} = 5\).
- Present Value:
The present value (PV) of an investment is calculated using the formula \(PV = \frac{FV}{(1 + r)^n}\). For more complex scenarios, simplifying square roots can help in deriving accurate values.
- Example: If \(FV = 1000\), \(r = 0.05\), and \(n = 10\), then \(PV = \frac{1000}{(1 + 0.05)^{10}} \approx \frac{1000}{1.629} \approx 613.91\).
Understanding how to simplify square roots is a valuable skill that enhances problem-solving abilities in various practical and professional fields.
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai để giúp bạn nắm vững các khái niệm và áp dụng vào các bài toán thực tế.
Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai, giúp người học hiểu rõ và nắm vững phương pháp này một cách dễ dàng.
Toán học - Đơn giản hóa Căn bậc Hai