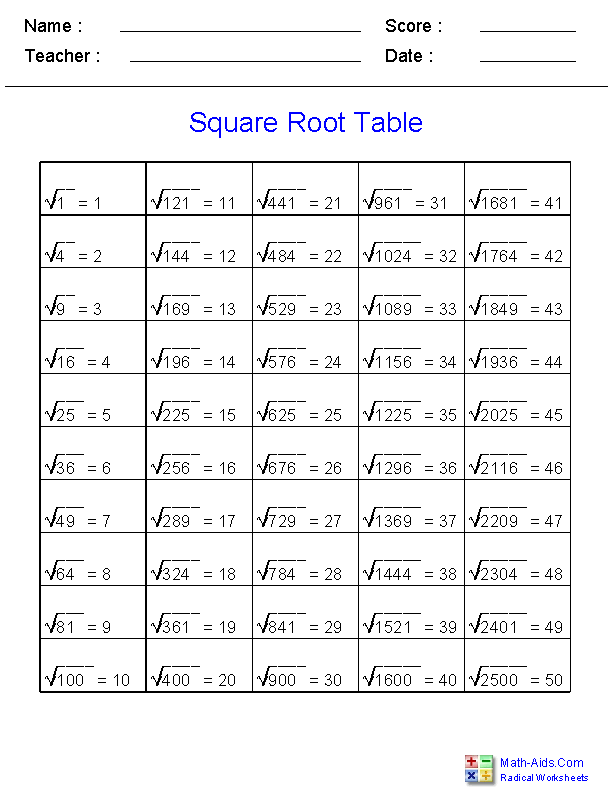
Topic practice simplifying square roots: Unlock the secrets to mastering the art of simplifying square roots with our comprehensive guide. Whether you're a beginner or looking to refine your skills, our step-by-step instructions and practice problems will help you simplify square roots effortlessly. Dive in and discover techniques that make this essential math skill easy and enjoyable.
Table of Content
- Practice Simplifying Square Roots
- Introduction to Simplifying Square Roots
- Basic Concepts of Square Roots
- Understanding Perfect Squares
- Prime Factorization Method
- Step-by-Step Simplification Process
- Handling Non-Perfect Squares
- Working with Coefficients
- Simplifying Square Roots with Variables
- Common Mistakes to Avoid
- Practice Problems and Solutions
- Advanced Techniques in Simplification
- Applications of Simplified Square Roots
- Interactive Exercises and Quizzes
- Additional Resources for Further Learning
- Conclusion and Key Takeaways
- YOUTUBE: Video này hướng dẫn cách đơn giản hóa căn bậc hai một cách dễ hiểu và chi tiết.
Practice Simplifying Square Roots
Simplifying square roots involves expressing a square root in its simplest form. This process includes identifying and factoring out perfect squares from the radicand (the number inside the square root).
Steps to Simplify Square Roots
- Factor the radicand into its prime factors.
- Group the prime factors into pairs of identical factors.
- Move one factor from each pair outside the square root.
- Multiply the factors outside the square root and simplify any remaining factors inside the square root.
Examples
-
Simplify \( \sqrt{12} \)
First, factor 12 into \( 4 \times 3 \).
\( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \)
-
Simplify \( \sqrt{45} \)
First, factor 45 into \( 9 \times 5 \).
\( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \)
Practice Problems
Try simplifying these square roots:
- \( \sqrt{50} \)
- \( \sqrt{72} \)
- \( \sqrt{98} \)
Advanced Topics
For more advanced practice, consider simplifying square roots that include variables or fractional radicands:
- \( \sqrt{18a^4b^2} \)
- \( \sqrt{\frac{50}{2}} \)
Using Math in Real Life
Simplifying square roots is not only a useful skill in algebra but also in various fields such as engineering, physics, and computer science where precise calculations are crucial.
Resources

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental skill in mathematics that helps in breaking down complex expressions into simpler forms. This process makes it easier to work with roots in equations and real-world applications. Below, we'll guide you through the essential steps and concepts needed to master simplifying square roots.
To begin, let's understand the basics:
- The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). It is denoted as \( \sqrt{x} \).
- Simplifying square roots involves finding the largest perfect square factor of the number under the square root and rewriting it as a product of square roots.
Here is a step-by-step method to simplify square roots:
- Identify the perfect square factors: Determine the largest perfect square factor of the number under the square root. For example, for \( \sqrt{72} \), the largest perfect square factor is 36.
- Rewrite the square root: Express the square root as a product of the square root of the perfect square and the remaining factor. For \( \sqrt{72} \), this would be \( \sqrt{36 \times 2} \).
- Simplify: Simplify the expression by taking the square root of the perfect square. Using our example, \( \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \).
Let's look at a few examples:
| Example | Simplification |
| \( \sqrt{50} \) | \( \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \) |
| \( \sqrt{18} \) | \( \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \) |
| \( \sqrt{75} \) | \( \sqrt{25 \times 3} = \sqrt{25} \times \sqrt{3} = 5\sqrt{3} \) |
By following these steps and practicing with various examples, you can become proficient at simplifying square roots, making complex mathematical problems easier to solve.
Basic Concepts of Square Roots
Understanding the basic concepts of square roots is crucial for simplifying them effectively. A square root of a number is a value that, when multiplied by itself, gives the original number. This concept is foundational in many areas of mathematics.
Here are some key points to understand:
- Definition: The square root of a number \( x \) is written as \( \sqrt{x} \) and is defined as a number \( y \) such that \( y^2 = x \).
- Positive and Negative Roots: Every positive number \( x \) has two square roots: a positive root \( \sqrt{x} \) and a negative root \( -\sqrt{x} \). For example, the square roots of 9 are 3 and -3.
- Perfect Squares: A perfect square is a number that has an integer as its square root. Examples include 1, 4, 9, 16, 25, etc. For instance, \( \sqrt{16} = 4 \) because \( 4^2 = 16 \).
- Non-Perfect Squares: Numbers that are not perfect squares have square roots that are irrational numbers. For example, \( \sqrt{2} \) is approximately 1.414 and cannot be expressed as an exact fraction.
To further illustrate these concepts, consider the following examples:
| Number | Square Root |
| 25 | \( \sqrt{25} = 5 \) (since \( 5^2 = 25 \)) |
| 36 | \( \sqrt{36} = 6 \) (since \( 6^2 = 36 \)) |
| 49 | \( \sqrt{49} = 7 \) (since \( 7^2 = 49 \)) |
| 20 | \( \sqrt{20} \approx 4.472 \) (an irrational number) |
Here is a step-by-step guide to find the square root of a number:
- Identify if the number is a perfect square: Check if the number can be expressed as the square of an integer.
- For perfect squares: Simply find the integer that, when squared, equals the given number.
- For non-perfect squares: Use a calculator or an approximation method to find the square root.
Understanding these basic concepts will provide a solid foundation for simplifying square roots and solving more complex mathematical problems involving roots.
Understanding Perfect Squares
Perfect squares are fundamental in the process of simplifying square roots. A perfect square is an integer that is the square of another integer. Recognizing and working with perfect squares makes it easier to simplify square roots.
Here are some key concepts about perfect squares:
- Definition: A perfect square is a number that can be expressed as \( n^2 \), where \( n \) is an integer. For example, 1, 4, 9, 16, 25, and 36 are perfect squares because they can be written as \( 1^2 \), \( 2^2 \), \( 3^2 \), \( 4^2 \), \( 5^2 \), and \( 6^2 \) respectively.
- Properties:
- Perfect squares are always non-negative.
- The square root of a perfect square is always an integer.
- They appear regularly in patterns, increasing quadratically (e.g., 1, 4, 9, 16, ...).
Let's look at a few examples of perfect squares and their square roots:
| Number | Square Root | Explanation |
| 1 | \( \sqrt{1} = 1 \) | 1 is a perfect square because \( 1^2 = 1 \). |
| 4 | \( \sqrt{4} = 2 \) | 4 is a perfect square because \( 2^2 = 4 \). |
| 9 | \( \sqrt{9} = 3 \) | 9 is a perfect square because \( 3^2 = 9 \). |
| 16 | \( \sqrt{16} = 4 \) | 16 is a perfect square because \( 4^2 = 16 \). |
| 25 | \( \sqrt{25} = 5 \) | 25 is a perfect square because \( 5^2 = 25 \). |
| 36 | \( \sqrt{36} = 6 \) | 36 is a perfect square because \( 6^2 = 36 \). |
Here is a step-by-step guide to identify and work with perfect squares:
- Recognize perfect squares: Familiarize yourself with the list of perfect squares up to at least \( 15^2 = 225 \). This will help in quickly identifying them in problems.
- Factorization: When simplifying square roots, factor the number under the root to check if it includes a perfect square. For example, \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \).
- Simplification: Extract the perfect square factor from the square root. For instance, \( \sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2} \).
Understanding and identifying perfect squares will significantly ease the process of simplifying square roots and solving related mathematical problems.
Prime Factorization Method
The prime factorization method is a powerful technique for simplifying square roots. By breaking down a number into its prime factors, we can more easily identify and extract perfect square factors, which simplifies the square root.
Here’s a step-by-step guide to using the prime factorization method:
- Find the prime factors: Break down the number under the square root into its prime factors. For example, for the number 72, the prime factorization is \( 72 = 2^3 \times 3^2 \).
- Group the prime factors: Pair the prime factors into groups of two. Each pair represents a perfect square. For \( 72 = 2^3 \times 3^2 \), we have one pair of 2s (\( 2^2 \)) and one pair of 3s (\( 3^2 \)), with one 2 remaining.
- Simplify the square root: Take the square root of each pair of prime factors, and multiply these together outside the square root. Any unpaired prime factors remain under the square root. Using our example:
\( \sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 2) \times 3^2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
Let’s look at some more examples to illustrate this method:
| Number | Prime Factorization | Simplification |
| 50 | \( 50 = 2 \times 5^2 \) | \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \) |
| 18 | \( 18 = 2 \times 3^2 \) | \( \sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2} \) |
| 75 | \( 75 = 3 \times 5^2 \) | \( \sqrt{75} = \sqrt{3 \times 5^2} = 5\sqrt{3} \) |
| 200 | \( 200 = 2^3 \times 5^2 \) | \( \sqrt{200} = \sqrt{2^3 \times 5^2} = \sqrt{(2^2 \times 2) \times 5^2} = 2 \times 5 \sqrt{2} = 10\sqrt{2} \) |
By following these steps, you can simplify any square root using the prime factorization method. This technique not only makes it easier to handle complex square roots but also deepens your understanding of the properties of numbers.

Step-by-Step Simplification Process
Simplifying square roots involves breaking down a number into its simplest form, which makes mathematical calculations easier and more manageable. Here’s a detailed, step-by-step process to simplify square roots:
- Identify the square root to simplify: Start with the square root that needs simplification. For example, \( \sqrt{72} \).
- Find the prime factors: Factorize the number under the square root into its prime factors. For 72, the prime factorization is:
\( 72 = 2 \times 36 = 2 \times 6 \times 6 = 2 \times 2 \times 3 \times 2 \times 3 = 2^3 \times 3^2 \).
- Group the prime factors: Pair the prime factors to identify the perfect squares. For \( 2^3 \times 3^2 \), we have one pair of 2s (\( 2^2 \)) and one pair of 3s (\( 3^2 \)), with one 2 remaining.
- Pair of 2s: \( 2^2 \)
- Pair of 3s: \( 3^2 \)
- Remaining: \( 2 \)
- Simplify the square root: Take the square root of each pair of prime factors and multiply these together outside the square root. The remaining prime factors stay inside the square root. For \( \sqrt{72} \):
\( \sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 2) \times 3^2} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
To further illustrate this process, let’s look at a few examples:
| Example | Prime Factorization | Simplified Form |
| \( \sqrt{50} \) | \( 50 = 2 \times 5^2 \) | \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \) |
| \( \sqrt{18} \) | \( 18 = 2 \times 3^2 \) | \( \sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2} \) |
| \( \sqrt{75} \) | \( 75 = 3 \times 5^2 \) | \( \sqrt{75} = \sqrt{3 \times 5^2} = 5\sqrt{3} \) |
| \( \sqrt{200} \) | \( 200 = 2^3 \times 5^2 \) | \( \sqrt{200} = \sqrt{2^3 \times 5^2} = 2 \times 5 \sqrt{2} = 10\sqrt{2} \) |
By following these steps, you can simplify any square root, making complex calculations simpler and more intuitive.
Handling Non-Perfect Squares
When dealing with non-perfect squares, the simplification process involves breaking down the number into its prime factors and extracting the perfect square factors. Non-perfect squares are numbers that do not have an integer as their square root. Here's a detailed step-by-step process to handle non-perfect squares:
- Identify the square root to simplify: Start with the square root that needs simplification. For example, \( \sqrt{45} \).
- Find the prime factors: Factorize the number under the square root into its prime factors. For 45, the prime factorization is:
\( 45 = 3^2 \times 5 \).
- Group the prime factors: Pair the prime factors to identify the perfect squares. For \( 45 = 3^2 \times 5 \), we have one pair of 3s (\( 3^2 \)), with one 5 remaining.
- Pair of 3s: \( 3^2 \)
- Remaining: \( 5 \)
- Simplify the square root: Take the square root of each pair of prime factors and multiply these together outside the square root. The remaining prime factors stay inside the square root. For \( \sqrt{45} \):
\( \sqrt{45} = \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5} = 3\sqrt{5} \).
Let’s look at some more examples to illustrate this process:
| Example | Prime Factorization | Simplified Form |
| \( \sqrt{50} \) | \( 50 = 2 \times 5^2 \) | \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \) |
| \( \sqrt{72} \) | \( 72 = 2^3 \times 3^2 \) | \( \sqrt{72} = \sqrt{2^3 \times 3^2} = 6\sqrt{2} \) |
| \( \sqrt{98} \) | \( 98 = 2 \times 7^2 \) | \( \sqrt{98} = \sqrt{2 \times 7^2} = 7\sqrt{2} \) |
| \( \sqrt{150} \) | \( 150 = 2 \times 3 \times 5^2 \) | \( \sqrt{150} = \sqrt{2 \times 3 \times 5^2} = 5\sqrt{6} \) |
By following these steps, you can simplify any square root, including those that are non-perfect squares. This method helps you break down complex square roots into simpler, more manageable forms.
Working with Coefficients
When simplifying square roots that include coefficients, it's important to handle both the coefficient and the radicand (the number inside the square root) properly. Here's a detailed, step-by-step guide to working with coefficients:
- Identify the expression to simplify: Start with the expression that includes a coefficient and a square root. For example, \( 3\sqrt{50} \).
- Simplify the square root: Simplify the square root portion separately by finding the prime factors and extracting the perfect squares. For \( \sqrt{50} \):
\( 50 = 2 \times 5^2 \)
\( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \)
- Combine the coefficient with the simplified square root: Multiply the simplified square root by the coefficient. For \( 3\sqrt{50} \):
\( 3\sqrt{50} = 3 \times 5\sqrt{2} = 15\sqrt{2} \)
Let’s look at more examples to further understand this process:
| Example | Prime Factorization | Simplified Form |
| \( 4\sqrt{18} \) | \( 18 = 2 \times 3^2 \) | \( 4\sqrt{18} = 4 \times 3\sqrt{2} = 12\sqrt{2} \) |
| \( 2\sqrt{72} \) | \( 72 = 2^3 \times 3^2 \) | \( 2\sqrt{72} = 2 \times 6\sqrt{2} = 12\sqrt{2} \) |
| \( 5\sqrt{98} \) | \( 98 = 2 \times 7^2 \) | \( 5\sqrt{98} = 5 \times 7\sqrt{2} = 35\sqrt{2} \) |
| \( 6\sqrt{150} \) | \( 150 = 2 \times 3 \times 5^2 \) | \( 6\sqrt{150} = 6 \times 5\sqrt{6} = 30\sqrt{6} \) |
By following these steps, you can effectively handle coefficients while simplifying square roots. This method ensures that both the coefficient and the radicand are correctly simplified, making complex expressions more manageable.
Simplifying Square Roots with Variables
Simplifying square roots involving variables requires a solid understanding of algebraic manipulation techniques. Let's explore the steps involved:
- Identify the variables: Determine the variables present in the square root expression.
- Factorize the expression: If possible, factorize the expression inside the square root sign to look for perfect squares.
- Apply the property of radicals: Recall that √(ab) = √a * √b. Use this property to break down the expression into simpler terms.
- Combine like terms: If there are similar terms inside the square root, combine them to simplify the expression further.
- Rationalize the denominator (if necessary): If the expression contains a radical in the denominator, rationalize it by multiplying both the numerator and denominator by the conjugate of the denominator.
- Check for extraneous solutions: Remember to verify if any solutions obtained are valid for the original problem, especially when squaring both sides to eliminate the square root.
Let's illustrate these steps with an example:
| Example: | Simplify √(9x^2) |
| Solution: |
1. Identify the variable: x 2. Factorize: √(9 * x^2) = √9 * √(x^2) = 3x |
By following these steps, you can confidently simplify square roots involving variables.

Common Mistakes to Avoid
When simplifying square roots, it's important to be aware of common pitfalls that can lead to errors. Here are some mistakes to watch out for:
- Forgetting to simplify perfect squares: Always check if there are perfect squares that can be extracted from the expression inside the square root. Failure to do so can result in unnecessarily complex solutions.
- Incorrect application of the product rule: Remember that √(ab) is not equal to √a * √b for all values of a and b. This property only applies when a and b are non-negative numbers.
- Ignoring the domain of the variable: Be mindful of the domain restrictions when simplifying square roots with variables. Certain values of the variable may lead to undefined or imaginary solutions.
- Mixing up addition and multiplication: It's easy to confuse addition and multiplication when simplifying expressions. Make sure to perform the operations in the correct order to avoid errors.
- Skipping rationalization of denominators: If the expression contains a square root in the denominator, don't forget to rationalize it to ensure a simplified form.
- Overlooking extraneous solutions: Double-check your solutions, especially after squaring both sides to eliminate the square root. Sometimes, extraneous solutions may arise, leading to incorrect results.
By avoiding these common mistakes and staying vigilant during the simplification process, you can improve your accuracy and confidence in handling square root expressions.
Practice Problems and Solutions
Practice makes perfect when it comes to simplifying square roots. Below are some practice problems along with their solutions to help you sharpen your skills:
-
Problem: Simplify √(25)
Solution: √(25) = 5
-
Problem: Simplify √(64)
Solution: √(64) = 8
-
Problem: Simplify √(18)
Solution: √(18) = √(9 * 2) = 3√2
-
Problem: Simplify √(x^2)
Solution: √(x^2) = |x|
-
Problem: Simplify √(4x^2y^3)
Solution: √(4x^2y^3) = 2xy√y
Take your time to work through these problems and compare your solutions with the provided answers. Practice until you feel comfortable simplifying square roots of various expressions.
Advanced Techniques in Simplification
Mastering advanced techniques can greatly enhance your ability to simplify square roots efficiently. Let's delve into some advanced methods:
- Completing the square: This technique is particularly useful when dealing with quadratic expressions under the square root. By completing the square, you can transform the expression into a perfect square trinomial, making it easier to simplify.
- Using trigonometric identities: In certain cases, trigonometric identities can be employed to simplify square roots involving trigonometric functions. This method is especially relevant in calculus and higher-level mathematics.
- Applying the conjugate: When faced with square roots in the denominator of a fraction, applying the conjugate can help rationalize the expression. This technique involves multiplying both the numerator and denominator by the conjugate of the denominator to eliminate the radical.
- Utilizing advanced factoring techniques: Advanced factoring methods, such as grouping, difference of squares, and sum or difference of cubes, can be applied to factorize complex expressions before simplification.
- Employing substitution: Substitution involves replacing complex expressions with simpler variables to facilitate the simplification process. This technique is particularly handy when dealing with nested radicals or intricate algebraic expressions.
By incorporating these advanced techniques into your repertoire, you'll be equipped to tackle even the most challenging square root simplification problems with confidence and precision.
Applications of Simplified Square Roots
Simplified square roots find applications in various fields, ranging from mathematics to real-world scenarios. Let's explore some practical uses:
- Geometry: In geometry, simplified square roots are commonly used to calculate the length of diagonals, sides of squares and rectangles, and distances between points.
- Physics: Simplified square roots are prevalent in physics equations, particularly those involving kinematics, dynamics, and electromagnetism. They help in determining magnitudes of vectors, velocities, accelerations, and electric fields.
- Engineering: Engineers frequently encounter simplified square roots in calculations related to structural analysis, fluid mechanics, heat transfer, and electrical circuits. These calculations aid in designing efficient and safe systems.
- Finance: In finance, simplified square roots are utilized in various calculations, such as computing interest rates, loan payments, and investment returns. They play a crucial role in financial modeling and risk assessment.
- Computer graphics: Simplified square roots are essential in computer graphics algorithms for tasks like calculating distances between objects, determining lighting effects, and performing transformations.
By understanding the applications of simplified square roots, you can appreciate their significance across different disciplines and apply them effectively in problem-solving contexts.

Interactive Exercises and Quizzes
Engage in interactive exercises and quizzes to reinforce your understanding of simplifying square roots. Below are some resources to test your skills:
- Khan Academy: Khan Academy offers a wide range of interactive exercises and quizzes on simplifying square roots. Practice at your own pace and receive instant feedback to track your progress.
- IXL: IXL provides interactive practice modules covering various topics in mathematics, including simplifying square roots. Dive into targeted exercises tailored to your skill level and receive personalized recommendations for improvement.
- Mathway: Mathway offers step-by-step solutions to simplifying square roots, allowing you to practice solving problems in real-time. Challenge yourself with their interactive quizzes and gain confidence in your abilities.
- Quizizz: Quizizz features fun and engaging quizzes on simplifying square roots, designed to make learning enjoyable. Compete with friends or classmates in multiplayer mode and see who can solve the most problems correctly.
- Math Games: Math Games offers interactive activities and games to practice simplifying square roots in an entertaining way. Sharpen your skills while having fun with their engaging educational games.
Take advantage of these interactive resources to enhance your proficiency in simplifying square roots and master this fundamental concept in mathematics.
Additional Resources for Further Learning
Expand your knowledge of simplifying square roots with these supplementary resources:
- MathIsFun: MathIsFun provides comprehensive tutorials and interactive examples to help you grasp the concepts of simplifying square roots. Explore their website for clear explanations and practice problems.
- Paul's Online Math Notes: Paul's Online Math Notes offers detailed lessons on simplifying square roots and other algebra topics. Dive into their extensive collection of notes, examples, and practice problems to deepen your understanding.
- Brilliant: Brilliant offers interactive courses covering various aspects of mathematics, including simplifying square roots. Join their community of learners to access engaging lessons and collaborate with peers.
- Chegg Study: Chegg Study provides solutions manuals and study resources for simplifying square roots and other mathematical topics. Subscribe to their service for access to step-by-step explanations and guided practice.
- YouTube Tutorials: Explore YouTube for instructional videos on simplifying square roots created by educators and mathematicians. Watch tutorials at your own pace and learn from visual demonstrations.
With these additional resources at your disposal, you can further enhance your understanding and proficiency in simplifying square roots.
Conclusion and Key Takeaways
Simplifying square roots is a fundamental skill in mathematics with applications across various fields. Let's recap the key takeaways from our exploration:
- Understanding the basics: Familiarize yourself with the basic concepts of square roots, perfect squares, and prime factorization to lay a strong foundation for simplification.
- Mastering techniques: Learn and practice different techniques for simplifying square roots, including factoring, applying properties of radicals, and handling variables.
- Avoiding common mistakes: Be cautious of common pitfalls such as forgetting to simplify perfect squares, incorrectly applying the product rule, and overlooking extraneous solutions.
- Exploring advanced methods: Explore advanced techniques like completing the square, using trigonometric identities, and employing substitution to tackle complex square root expressions.
- Applying in real-world scenarios: Recognize the practical applications of simplified square roots in geometry, physics, engineering, finance, and computer graphics.
- Utilizing resources: Take advantage of interactive exercises, quizzes, online tutorials, and study materials to deepen your understanding and improve your skills.
By mastering the art of simplifying square roots, you'll not only excel in mathematics but also develop problem-solving abilities that are valuable in various academic and professional pursuits.
Video này hướng dẫn cách đơn giản hóa căn bậc hai một cách dễ hiểu và chi tiết.
Đơn Giản Hóa Căn Bậc Hai | Toán Học Với Thầy J
READ MORE:
Video này hướng dẫn cách đơn giản hóa căn bậc hai một cách dễ hiểu và chi tiết.
Cách Đơn Giản Hóa Căn Bậc Hai