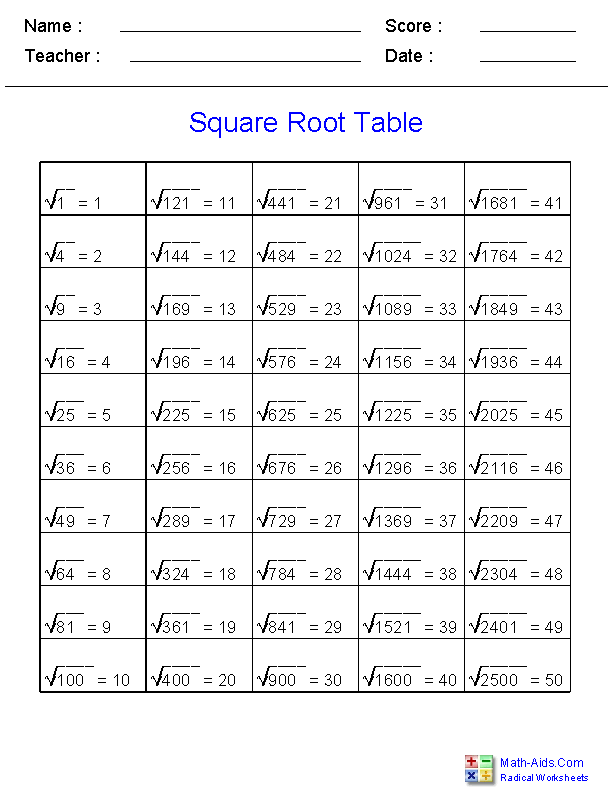
Topic examples of simplifying square roots: Discover the art of simplifying square roots with our comprehensive guide. From basic concepts to advanced techniques, we'll walk you through step-by-step examples to help you master this essential math skill. Perfect for students and enthusiasts alike, our guide ensures you gain confidence and accuracy in simplifying square roots.
Table of Content
- Examples of Simplifying Square Roots
- Introduction to Simplifying Square Roots
- Basic Concepts of Square Roots
- Importance of Simplifying Square Roots
- Steps to Simplify Square Roots
- Prime Factorization Method
- Using Perfect Squares to Simplify
- Examples of Simplifying Square Roots
- Simplifying Square Roots with Variables
- Working with Square Roots of Fractions
- Practice Problems and Solutions
- Common Mistakes and How to Avoid Them
- Advanced Techniques for Simplifying Square Roots
- Applications of Simplifying Square Roots in Real Life
- Frequently Asked Questions
- Conclusion and Further Resources
- YOUTUBE:
Examples of Simplifying Square Roots
Simplifying square roots involves expressing the square root of a number in its simplest form. Here are several examples and methods to simplify square roots:
Basic Examples
- Simplify √12
- Break down 12 into its prime factors: 12 = 4 × 3.
- Use the square root property: √12 = √(4 × 3) = √4 × √3.
- Simplify: √4 = 2, so √12 = 2√3.
- Simplify √45
- Break down 45 into its prime factors: 45 = 9 × 5.
- Use the square root property: √45 = √(9 × 5) = √9 × √5.
- Simplify: √9 = 3, so √45 = 3√5.
- Break down 18 into its prime factors: 18 = 9 × 2.
- Use the square root property: √18 = √(9 × 2) = √9 × √2.
- Simplify: √9 = 3, so √18 = 3√2.
Examples with Fractions
- Simplify √(30/10)
- Combine the numbers inside the square root: √(30 / 10).
- Simplify the fraction inside: √3.
More Complex Examples
- Simplify √200
- Break down 200 into its prime factors: 200 = 100 × 2.
- Use the square root property: √200 = √(100 × 2) = √100 × √2.
- Simplify: √100 = 10, so √200 = 10√2.
- Simplify √180
- Break down 180 into its prime factors: 180 = 36 × 5.
- Use the square root property: √180 = √(36 × 5) = √36 × √5.
- Simplify: √36 = 6, so √180 = 6√5.
Examples with Variables
- Simplify √(12x²y⁴)
- Break down 12 into its prime factors and handle variables: 12 = 4 × 3, x² and y⁴ are already perfect squares.
- Use the square root property: √(12x²y⁴) = √(4 × 3x²y⁴) = √4 × √3 × √x² × √y⁴.
- Simplify: √4 = 2, √x² = x, √y⁴ = y², so √(12x²y⁴) = 2xy²√3.
- Simplify √(54a¹⁰b¹⁶c⁷)
- Break down 54 into its prime factors and handle variables: 54 = 9 × 6, a¹⁰, b¹⁶, and c⁷.
- Use the square root property: √(54a¹⁰b¹⁶c⁷) = √(9 × 6a¹⁰b¹⁶c⁷) = √9 × √6 × √a¹⁰ × √b¹⁶ × √c⁷.
- Simplify: √9 = 3, √a¹⁰ = a⁵, √b¹⁶ = b⁸, √c⁷ = c³√c, so √(54a¹⁰b¹⁶c⁷) = 3a⁵b⁸c³√6c.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental skill in mathematics, allowing us to express roots in their simplest form. This process involves breaking down a square root into its prime factors and simplifying them step by step. Below, we will explore the basic concepts and techniques used in simplifying square roots.
When simplifying square roots, we aim to find an equivalent expression that is easier to work with. Here's a step-by-step guide to understanding and simplifying square roots:
- Identify the Square Root: Begin with the square root you need to simplify, for example, \( \sqrt{50} \).
- Prime Factorization: Break down the number inside the square root into its prime factors. For \( \sqrt{50} \), the prime factorization is \( 50 = 2 \times 5 \times 5 \).
- Group the Factors: Group the prime factors into pairs. In our example, \( 50 = 2 \times (5 \times 5) \).
- Simplify the Square Root: Take one factor from each pair out of the square root. Thus, \( \sqrt{50} = \sqrt{2 \times (5 \times 5)} = 5\sqrt{2} \).
Here is a table summarizing the steps to simplify square roots:
| Step | Description | Example |
|---|---|---|
| Identify the Square Root | Determine the number under the square root | \( \sqrt{50} \) |
| Prime Factorization | Break down the number into prime factors | \( 50 = 2 \times 5 \times 5 \) |
| Group the Factors | Pair the prime factors | \( 50 = 2 \times (5 \times 5) \) |
| Simplify the Square Root | Take one factor from each pair out of the square root | \( \sqrt{50} = 5\sqrt{2} \) |
By following these steps, you can simplify any square root efficiently. Practicing this method will enhance your problem-solving skills and boost your confidence in handling more complex mathematical problems.
Basic Concepts of Square Roots
Understanding square roots is essential in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because \( 4 \times 4 = 16 \). The symbol for the square root is \( \sqrt{} \).
Here are the basic concepts to grasp when working with square roots:
- Definition: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). This is written as \( y = \sqrt{x} \).
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because they are squares of whole numbers (e.g., \( 4 = 2^2 \), \( 9 = 3^2 \)).
- Non-Perfect Squares: Numbers that are not perfect squares, such as 2, 3, 5, and 7, have square roots that are irrational numbers (e.g., \( \sqrt{2} \approx 1.414 \)).
- Properties of Square Roots:
- \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- \( (\sqrt{a})^2 = a \)
- \( \sqrt{a^2} = |a| \)
Consider these examples for better understanding:
- Example 1: Simplifying \( \sqrt{36} \)
- Recognize that 36 is a perfect square: \( 36 = 6^2 \)
- Therefore, \( \sqrt{36} = 6 \)
- Example 2: Simplifying \( \sqrt{45} \)
- Prime factorize 45: \( 45 = 3^2 \times 5 \)
- Group the factors: \( \sqrt{45} = \sqrt{3^2 \times 5} \)
- Simplify: \( \sqrt{45} = 3\sqrt{5} \)
Here is a summary table of important properties and examples:
| Property | Example | Result |
|---|---|---|
| \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \) | \( \sqrt{50} = \sqrt{25 \times 2} \) | \( 5\sqrt{2} \) |
| \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) | \( \sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} \) | \( \frac{2}{3} \) |
| \( (\sqrt{a})^2 = a \) | \( (\sqrt{7})^2 \) | \( 7 \) |
| \( \sqrt{a^2} = |a| \) | \( \sqrt{(-5)^2} \) | \( 5 \) |
By mastering these basic concepts, you will build a strong foundation for more advanced topics involving square roots and other mathematical operations.
Importance of Simplifying Square Roots
Simplifying square roots is an essential skill in mathematics, providing numerous benefits in various areas of study and everyday applications. Here, we explore the importance of this process and how it contributes to mathematical proficiency and problem-solving efficiency.
- Enhanced Problem Solving: Simplifying square roots makes complex calculations more manageable and easier to work with, facilitating quicker and more accurate solutions.
- Foundation for Advanced Mathematics: Mastery of square root simplification is crucial for success in higher-level math courses, such as algebra, calculus, and beyond. It helps in understanding and manipulating more complex expressions and equations.
- Application in Real Life: Simplified square roots are used in various fields, including physics, engineering, computer science, and finance. For example, they are essential in calculating distances, areas, and other measurements.
- Improved Mathematical Communication: Using simplified forms of square roots allows for clearer and more effective communication of mathematical ideas and solutions, whether in written or verbal form.
- Efficiency in Computation: Simplifying square roots reduces the complexity of calculations, making it easier to perform operations manually or with the aid of calculators and software.
Consider these practical examples to understand the significance of simplifying square roots:
- Example in Geometry:
- Finding the diagonal of a square with side length 10 units involves the square root of 200.
- Simplifying \( \sqrt{200} = \sqrt{2 \times 100} = 10\sqrt{2} \) provides a more concise and manageable form.
- Example in Physics:
- Calculating the resultant vector of two perpendicular forces requires finding the square root of the sum of the squares of the forces.
- For forces of 3 N and 4 N, the magnitude is \( \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) N, simplifying the problem significantly.
Here is a summary table of the key reasons for simplifying square roots:
| Reason | Explanation |
|---|---|
| Enhanced Problem Solving | Makes complex calculations more manageable |
| Foundation for Advanced Mathematics | Crucial for higher-level math courses |
| Application in Real Life | Used in various fields for practical calculations |
| Improved Mathematical Communication | Allows clearer communication of ideas |
| Efficiency in Computation | Reduces complexity of calculations |
By understanding and practicing the simplification of square roots, students and professionals alike can enhance their mathematical abilities and apply these skills effectively in both academic and real-world scenarios.
Steps to Simplify Square Roots
Simplifying square roots involves reducing the expression inside the square root to its simplest form. Here are the detailed steps:
- Factor the number into prime factors:
Break down the number inside the square root into its prime factors. For example, 72 can be factored into 2 × 2 × 2 × 3 × 3.
- Pair the prime factors:
Group the prime factors into pairs. Each pair of prime factors will be taken out of the square root as a single number. For instance, in the prime factorization of 72 (2 × 2 × 2 × 3 × 3), the pairs are (2, 2) and (3, 3).
- Simplify by taking out the pairs:
For each pair of prime factors, take one factor out of the square root. Using our example, √72 = √(2 × 2 × 2 × 3 × 3) = 2 × 3 × √2 = 6√2.
- Multiply the numbers outside the square root:
Combine the numbers outside the square root to get the simplified form. In our example, 2 and 3 were taken out, resulting in 6√2.
Examples:
- Simplify √50:
50 = 2 × 5 × 5, so √50 = 5√2.
- Simplify √288:
288 = 2 × 2 × 2 × 2 × 2 × 3 × 3, so √288 = 2 × 2 × 3√2 = 12√2.
Using Perfect Squares:
Another method involves recognizing perfect squares within the number:
- Identify the largest perfect square factor:
For example, to simplify √72, recognize that 36 (6 × 6) is the largest perfect square factor of 72.
- Rewrite the square root:
Express the number as the product of the perfect square and another number. For √72, this is √(36 × 2).
- Simplify:
Simplify by taking the square root of the perfect square and multiplying it by the remaining factor: √(36 × 2) = 6√2.
Steps for Square Roots of Fractions:
Simplifying square roots of fractions involves similar principles:
- Simplify the fraction:
For example, √(30/10) = √3.
- Rationalize the denominator:
If the square root is in the denominator, multiply the numerator and denominator by the square root to eliminate it.
By following these steps, you can simplify any square root to its simplest form, making complex calculations easier to handle.

Prime Factorization Method
The prime factorization method is a systematic way to simplify square roots by expressing the number as a product of its prime factors. Here are the steps to simplify square roots using this method:
- Find the Prime Factors: Break down the number into its prime factors. Prime factors are the prime numbers that multiply together to give the original number. For example, for 72, the prime factors are \( 2 \times 2 \times 2 \times 3 \times 3 \).
- Pair the Prime Factors: Group the prime factors into pairs. Each pair of identical prime factors can be taken out from under the square root. For example, for \( \sqrt{72} \), the prime factorization is \( \sqrt{2 \times 2 \times 2 \times 3 \times 3} \). Grouping the pairs, we get \( \sqrt{(2 \times 2) \times 2 \times (3 \times 3)} \).
- Simplify by Taking Out Pairs: For each pair of identical factors, take one factor out of the square root. Continuing the example, \( \sqrt{(2 \times 2) \times 2 \times (3 \times 3)} \) simplifies to \( 2 \times 3 \times \sqrt{2} \). Therefore, \( \sqrt{72} = 6\sqrt{2} \).
Here are some more examples to illustrate the process:
- Example 1: Simplify \( \sqrt{400} \)
- Prime factorization: \( 400 = 2 \times 2 \times 2 \times 2 \times 5 \times 5 \)
- Group into pairs: \( \sqrt{(2 \times 2) \times (2 \times 2) \times (5 \times 5)} \)
- Simplify: \( \sqrt{400} = 2 \times 2 \times 5 = 20 \)
- Example 2: Simplify \( \sqrt{625} \)
- Prime factorization: \( 625 = 5 \times 5 \times 5 \times 5 \)
- Group into pairs: \( \sqrt{(5 \times 5) \times (5 \times 5)} \)
- Simplify: \( \sqrt{625} = 5 \times 5 = 25 \)
- Example 3: Simplify \( \sqrt{1024} \)
- Prime factorization: \( 1024 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \)
- Group into pairs: \( \sqrt{(2 \times 2) \times (2 \times 2) \times (2 \times 2) \times (2 \times 2) \times (2 \times 2)} \)
- Simplify: \( \sqrt{1024} = 2 \times 2 \times 2 \times 2 \times 2 = 32 \)
This method ensures that the square root is simplified in the most efficient manner possible. Practice with different numbers to get comfortable with the prime factorization method.
Using Perfect Squares to Simplify
Simplifying square roots using perfect squares involves identifying and factoring out perfect square factors from the radicand (the number inside the square root). Here are the steps to follow:
- Identify Perfect Square Factors:
Look for the largest perfect square factor of the number under the square root. Perfect squares are numbers like 1, 4, 9, 16, 25, etc.
- Rewrite the Radicand:
Express the radicand as a product of its perfect square factor and another number.
- Apply the Square Root to Each Factor:
Use the property \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) to separate the square root into the product of the square roots of the factors.
- Simplify:
Simplify the square root of the perfect square factor to get a whole number. The remaining part under the square root stays as it is.
Let's look at a few examples to illustrate these steps:
- Example 1: Simplify \(\sqrt{72}\)
- Identify the largest perfect square factor of 72, which is 36.
- Rewrite 72 as \(36 \times 2\).
- Apply the property: \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2}\).
- Simplify: \(\sqrt{36} = 6\), so \(\sqrt{72} = 6\sqrt{2}\).
- Example 2: Simplify \(\sqrt{200}\)
- Identify the largest perfect square factor of 200, which is 100.
- Rewrite 200 as \(100 \times 2\).
- Apply the property: \(\sqrt{200} = \sqrt{100 \times 2} = \sqrt{100} \times \sqrt{2}\).
- Simplify: \(\sqrt{100} = 10\), so \(\sqrt{200} = 10\sqrt{2}\).
- Example 3: Simplify \(\sqrt{48}\)
- Identify the largest perfect square factor of 48, which is 16.
- Rewrite 48 as \(16 \times 3\).
- Apply the property: \(\sqrt{48} = \sqrt{16 \times 3} = \sqrt{16} \times \sqrt{3}\).
- Simplify: \(\sqrt{16} = 4\), so \(\sqrt{48} = 4\sqrt{3}\).
Examples of Simplifying Square Roots
Below are several examples demonstrating how to simplify square roots using different methods:
Example 1: Simplify \( \sqrt{72} \)
- Factor 72 into its prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Group the prime factors into pairs: \( (2 \times 2) \times (3 \times 3) \times 2 \)
- Take out the square root of each pair: \( 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \)
Thus, \( \sqrt{72} = 6\sqrt{2} \).
Example 2: Simplify \( \sqrt{45} \)
- Factor 45 into its prime factors: \( 45 = 3 \times 3 \times 5 \)
- Group the prime factors into pairs: \( (3 \times 3) \times 5 \)
- Take out the square root of each pair: \( 3 \times \sqrt{5} = 3\sqrt{5} \)
Thus, \( \sqrt{45} = 3\sqrt{5} \).
Example 3: Simplify \( \sqrt{18} \)
- Factor 18 into its prime factors: \( 18 = 2 \times 3 \times 3 \)
- Group the prime factors into pairs: \( 2 \times (3 \times 3) \)
- Take out the square root of each pair: \( 3 \times \sqrt{2} = 3\sqrt{2} \)
Thus, \( \sqrt{18} = 3\sqrt{2} \).
Example 4: Simplify \( \sqrt{50} \)
- Factor 50 into its prime factors: \( 50 = 2 \times 5 \times 5 \)
- Group the prime factors into pairs: \( 2 \times (5 \times 5) \)
- Take out the square root of each pair: \( 5 \times \sqrt{2} = 5\sqrt{2} \)
Thus, \( \sqrt{50} = 5\sqrt{2} \).
Example 5: Simplify \( \sqrt{200} \)
- Factor 200 into its prime factors: \( 200 = 2 \times 2 \times 2 \times 5 \times 5 \)
- Group the prime factors into pairs: \( (2 \times 2) \times (5 \times 5) \times 2 \)
- Take out the square root of each pair: \( 2 \times 5 \times \sqrt{2} = 10\sqrt{2} \)
Thus, \( \sqrt{200} = 10\sqrt{2} \).
Example 6: Simplify \( \sqrt{12x^2y^4} \)
- Factor 12 into its prime factors: \( 12 = 2 \times 2 \times 3 \)
- Group the prime factors: \( (2 \times 2) \times 3 \)
- Simplify the square root: \( 2\sqrt{3} \)
- Simplify the variables: \( \sqrt{x^2} = x \) and \( \sqrt{y^4} = y^2 \)
- Combine the results: \( 2xy^2\sqrt{3} \)
Thus, \( \sqrt{12x^2y^4} = 2xy^2\sqrt{3} \).
Example 7: Simplify \( \sqrt{\frac{24}{5}} \)
- Simplify the fraction inside the square root: \( \sqrt{\frac{24}{5}} = \frac{\sqrt{24}}{\sqrt{5}} \)
- Simplify \( \sqrt{24} \): \( 24 = 2 \times 2 \times 2 \times 3 = 2\sqrt{6} \)
- Combine the results: \( \frac{2\sqrt{6}}{\sqrt{5}} \)
- Rationalize the denominator: \( \frac{2\sqrt{6}}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{2\sqrt{30}}{5} \)
Thus, \( \sqrt{\frac{24}{5}} = \frac{2\sqrt{30}}{5} \).
Practicing these steps will help in mastering the simplification of square roots.
Simplifying Square Roots with Variables
When simplifying square roots that contain variables, the process involves using the properties of exponents and square roots to break down the expression into simpler parts. Here are detailed steps and examples to help you understand the process:
Steps to Simplify Square Roots with Variables
Identify Perfect Squares: Look for perfect square factors in both the numerical coefficients and the variable parts.
Separate the Factors: Write the expression under the square root as a product of its factors, grouping perfect squares together.
Simplify Using Square Root Properties: Take the square root of the perfect squares and leave the remaining factors inside the square root.
Use Absolute Values When Necessary: If the variable has an even exponent, remember to use the absolute value to ensure the result is non-negative.
Examples
Example 1: Simplifying \(\sqrt{9x^6}\)
To simplify \(\sqrt{9x^6}\), follow these steps:
- Identify the perfect squares: \(9\) and \(x^6\).
- Rewrite the expression: \(\sqrt{9 \cdot (x^3)^2}\).
- Simplify: \(\sqrt{9} \cdot \sqrt{(x^3)^2} = 3|x^3|\).
So, \(\sqrt{9x^6} = 3|x^3|\).
Example 2: Simplifying \(\sqrt{100x^2y^4}\)
To simplify \(\sqrt{100x^2y^4}\), follow these steps:
- Identify the perfect squares: \(100\), \(x^2\), and \(y^4\).
- Rewrite the expression: \(\sqrt{100 \cdot x^2 \cdot (y^2)^2}\).
- Simplify: \(\sqrt{100} \cdot \sqrt{x^2} \cdot \sqrt{(y^2)^2} = 10|x||y^2|\).
So, \(\sqrt{100x^2y^4} = 10|x|y^2\).
Example 3: Simplifying \(\sqrt{49x^{10}y^8}\)
To simplify \(\sqrt{49x^{10}y^8}\), follow these steps:
- Identify the perfect squares: \(49\), \(x^{10}\), and \(y^8\).
- Rewrite the expression: \(\sqrt{49 \cdot (x^5)^2 \cdot (y^4)^2}\).
- Simplify: \(\sqrt{49} \cdot \sqrt{(x^5)^2} \cdot \sqrt{(y^4)^2} = 7|x^5||y^4|\).
So, \(\sqrt{49x^{10}y^8} = 7|x^5|y^4\).
Practice Problems
- Simplify \(\sqrt{36x^4y^2}\).
- Simplify \(\sqrt{81x^8}\).
- Simplify \(\sqrt{25x^2y^6}\).
Remember to look for perfect square factors and apply the properties of square roots and exponents to simplify the expressions correctly.

Working with Square Roots of Fractions
Simplifying square roots of fractions involves using the properties of radicals to simplify both the numerator and the denominator separately. Here are some methods and examples to guide you through the process:
Steps to Simplify Square Roots of Fractions
- Rewrite the fraction: Separate the square root of the fraction into the square roots of the numerator and the denominator.
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\] - Simplify the square roots: Simplify the square root of the numerator and the square root of the denominator individually, if possible.
Examples
- Example 1: Simplify \(\sqrt{\frac{25}{36}}\)
- Separate the fraction:
\[
\sqrt{\frac{25}{36}} = \frac{\sqrt{25}}{\sqrt{36}}
\] - Simplify the square roots:
\[
\frac{\sqrt{25}}{\sqrt{36}} = \frac{5}{6}
\]
- Separate the fraction:
- Example 2: Simplify \(\sqrt{\frac{18}{32}}\)
- Reduce the fraction first:
\[
\frac{18}{32} = \frac{9}{16}
\] - Separate the fraction:
\[
\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}}
\] - Simplify the square roots:
\[
\frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}
\]
- Reduce the fraction first:
Special Cases
- Mixed Numbers: Convert mixed numbers to improper fractions before simplifying.
- Example: Simplify \(\sqrt{1\frac{13}{36}}\)
Convert to improper fraction:
\[
1\frac{13}{36} = \frac{49}{36}
\]Separate the fraction:
\[
\sqrt{\frac{49}{36}} = \frac{\sqrt{49}}{\sqrt{36}}
\]Simplify:
\[
\frac{\sqrt{49}}{\sqrt{36}} = \frac{7}{6} = 1\frac{1}{6}
\]
- Example: Simplify \(\sqrt{1\frac{13}{36}}\)
By following these steps, you can simplify the square roots of fractions effectively. Remember to always check if the fraction can be reduced first, as this can make the process easier.
Practice Problems and Solutions
Here are several practice problems to help you master the technique of simplifying square roots. Each problem includes a detailed step-by-step solution.
Problem 1: Simplify \( \sqrt{72} \)
- Factor 72 into its prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Group the prime factors into pairs: \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} \).
- Take one factor out of each pair: \( \sqrt{72} = 2 \times 3 \times \sqrt{2} \).
- Simplify: \( \sqrt{72} = 6\sqrt{2} \).
Solution: \( \sqrt{72} = 6\sqrt{2} \)
Problem 2: Simplify \( \sqrt{200} \)
- Factor 200 into its prime factors: \( 200 = 2 \times 2 \times 2 \times 5 \times 5 \).
- Group the prime factors into pairs: \( \sqrt{200} = \sqrt{(2 \times 2) \times (5 \times 5) \times 2} \).
- Take one factor out of each pair: \( \sqrt{200} = 2 \times 5 \times \sqrt{2} \).
- Simplify: \( \sqrt{200} = 10\sqrt{2} \).
Solution: \( \sqrt{200} = 10\sqrt{2} \)
Problem 3: Simplify \( \sqrt{45} \)
- Factor 45 into its prime factors: \( 45 = 3 \times 3 \times 5 \).
- Group the prime factors into pairs: \( \sqrt{45} = \sqrt{(3 \times 3) \times 5} \).
- Take one factor out of each pair: \( \sqrt{45} = 3 \times \sqrt{5} \).
- Simplify: \( \sqrt{45} = 3\sqrt{5} \).
Solution: \( \sqrt{45} = 3\sqrt{5} \)
Problem 4: Simplify \( \sqrt{128} \)
- Factor 128 into its prime factors: \( 128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \).
- Group the prime factors into pairs: \( \sqrt{128} = \sqrt{(2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2} \).
- Take one factor out of each pair: \( \sqrt{128} = 2 \times 2 \times 2 \times \sqrt{2} \).
- Simplify: \( \sqrt{128} = 8\sqrt{2} \).
Solution: \( \sqrt{128} = 8\sqrt{2} \)
Problem 5: Simplify \( \sqrt{18} \)
- Factor 18 into its prime factors: \( 18 = 2 \times 3 \times 3 \).
- Group the prime factors into pairs: \( \sqrt{18} = \sqrt{2 \times (3 \times 3)} \).
- Take one factor out of each pair: \( \sqrt{18} = 3 \times \sqrt{2} \).
- Simplify: \( \sqrt{18} = 3\sqrt{2} \).
Solution: \( \sqrt{18} = 3\sqrt{2} \)
Additional Practice Problems:
- Simplify \( \sqrt{98} \)
- Simplify \( \sqrt{72x^2} \)
- Simplify \( \sqrt{50y^4} \)
- Simplify \( \sqrt{63a^6b^3} \)
Try these additional problems on your own and use the steps provided above to find the solutions. Practice regularly to enhance your skills in simplifying square roots.
Common Mistakes and How to Avoid Them
Simplifying square roots can sometimes lead to common mistakes. Here are some of the typical errors students make and how to avoid them:
- Incorrectly Simplifying Non-Perfect Squares:
For example, incorrectly simplifying
\(\sqrt{12}\) as 6 instead of breaking it down correctly. Solution: Factor the number inside the square root into its prime factors:
\[\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\] - Ignoring the Negative Solution:
When solving equations like
\(x^2 = 9\) , students might only consider\(x = 3\) and ignore\(x = -3\) .Solution: Remember that both the positive and negative roots are solutions:
\[x^2 = 9 \implies x = \pm 3\] - Incorrect Distribution of Roots over Sums:
Students often incorrectly apply the distributive property to roots, such as
\(\sqrt{a+b} = \sqrt{a} + \sqrt{b}\) .Solution: Understand that roots do not distribute over addition:
Example:
\[\sqrt{9 + 16} \neq \sqrt{9} + \sqrt{16}\] Correct calculation:
\[\sqrt{25} = 5 \text{ while } \sqrt{9} + \sqrt{16} = 3 + 4 = 7\] - Misunderstanding Rationalization:
When rationalizing denominators, students might incorrectly simplify expressions.
Solution: Multiply both the numerator and the denominator by the conjugate of the denominator if it contains a square root:
Example:
\[\frac{1}{\sqrt{2}} \rightarrow \frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{\sqrt{2}}{2}\] - Errors with Variables:
Students sometimes forget the rules when simplifying square roots with variables.
Solution: Remember to treat variables as you would numbers and apply the properties of exponents and roots:
Example:
\[\sqrt{x^4} = x^2\]
By understanding these common mistakes and applying the correct methods, you can avoid errors and simplify square roots accurately.
Advanced Techniques for Simplifying Square Roots
To go beyond the basics of simplifying square roots, we can employ several advanced techniques. These methods can be particularly useful when dealing with higher-index roots, complex expressions, or variables.
Using Higher-Index Roots
For roots other than square roots, the same principles apply but with adjustments for the index of the root.
- Identify the prime factorization of the radicand.
- Group the factors according to the index.
- Simplify by taking out the common groups.
Example:
Simplify \( \sqrt[4]{16y^4} \):
- Prime factorization: \( 16 = 2^4 \)
- Group the factors: \( \sqrt[4]{2^4y^4} = \sqrt[4]{(2y)^4} \)
- Simplify: \( \sqrt[4]{(2y)^4} = 2y \)
Thus, \( \sqrt[4]{16y^4} = 2y \).
Simplifying Products and Quotients
When simplifying the product or quotient of square roots, use the property \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) and \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Example:
Simplify \( \sqrt{18a^5b^8} \):
- Factorize inside the radical: \( 18 = 2 \cdot 3^2 \), \( a^5 = a^4 \cdot a \), and \( b^8 = (b^4)^2 \)
- Express under the square root: \( \sqrt{2 \cdot 3^2 \cdot a^4 \cdot a \cdot (b^4)^2} \)
- Simplify each factor: \( 3a^2b^4\sqrt{2a} \)
Thus, \( \sqrt{18a^5b^8} = 3a^2b^4\sqrt{2a} \).
Simplifying Complex Expressions
Sometimes, complex expressions can be simplified by recognizing patterns or using algebraic identities.
Example:
Simplify \( \sqrt{x^2 + 2x + 1} \):
- Recognize the perfect square: \( x^2 + 2x + 1 = (x + 1)^2 \)
- Simplify the square root: \( \sqrt{(x + 1)^2} = |x + 1| \)
Thus, \( \sqrt{x^2 + 2x + 1} = |x + 1| \).
Working with Variables
When variables are involved, it is crucial to account for both positive and negative values.
Example:
Simplify \( \sqrt{12x^2y^3} \):
- Factorize inside the radical: \( 12 = 2^2 \cdot 3 \), \( x^2 = x \cdot x \), \( y^3 = y^2 \cdot y \)
- Express under the square root: \( \sqrt{2^2 \cdot 3 \cdot x^2 \cdot y^2 \cdot y} \)
- Simplify each factor: \( 2xy\sqrt{3y} \)
Thus, \( \sqrt{12x^2y^3} = 2xy\sqrt{3y} \).
By mastering these advanced techniques, you can handle more complex square root simplifications with confidence.

Applications of Simplifying Square Roots in Real Life
Simplifying square roots is not just an academic exercise; it has practical applications in various real-life scenarios. Understanding these applications can help reinforce the importance of mastering this mathematical concept. Here are some key areas where simplifying square roots is used:
- Finance: In finance, square roots are used to calculate stock market volatility. For example, the standard deviation of stock returns, which helps in assessing investment risk, involves taking the square root of the variance of returns.
- Architecture: Architects and engineers use square roots to determine the natural frequencies of buildings and bridges, helping predict how these structures will respond to environmental forces like wind and traffic.
- Physics: In physics, square roots are essential in formulas that calculate various physical quantities, such as the velocity of an object or the intensity of sound waves.
- Statistics: In statistical analysis, the standard deviation, a measure of data dispersion, is the square root of the variance. This helps statisticians understand and interpret data sets effectively.
- Geometry: The Pythagorean theorem, used to calculate distances between points in geometric figures, involves square roots. This is crucial in fields like construction and carpentry.
- Computer Science: Algorithms in computer graphics, encryption, and game physics often rely on square roots for various calculations, such as determining distances and implementing security protocols.
- Navigation: Pilots and navigators use square roots to calculate distances between locations on maps, aiding in plotting accurate courses.
- Electrical Engineering: Square roots are used to calculate electrical quantities such as power, voltage, and current in circuit design and analysis.
- Photography: The aperture of a camera lens, which controls the amount of light entering the camera, is related to the square of the f-number, impacting exposure and depth of field in photographs.
Understanding these applications demonstrates the practical value of simplifying square roots and underscores its importance in various professional and everyday contexts.
Frequently Asked Questions
Here are some frequently asked questions about simplifying square roots, along with detailed answers to help you understand the concepts better:
- Q1: How do you simplify the square root of a non-perfect square?
A: To simplify the square root of a non-perfect square, you need to factor the number into its prime factors and then pair the identical factors. For example, to simplify √72:
\[ \sqrt{72} = \sqrt{2 \times 36} = \sqrt{2 \times 6^2} = 6\sqrt{2} \]
The simplified form is \( 6\sqrt{2} \).
- Q2: Can you simplify the square root of a variable expression?
A: Yes, variable expressions can also be simplified. For example, to simplify \(\sqrt{x^{10}}\):
\[ \sqrt{x^{10}} = \sqrt{(x^5)^2} = x^5 \]
If the exponent is even, take half of the exponent. For an odd exponent, separate the odd factor first.
- Q3: What if there are coefficients outside the radical?
A: When simplifying square roots with coefficients, treat the coefficient separately. For example, to simplify \(3\sqrt{50}\):
\[ 3\sqrt{50} = 3\sqrt{25 \times 2} = 3 \times 5\sqrt{2} = 15\sqrt{2} \]
- Q4: How do you add or subtract square roots?
A: You can add or subtract square roots only if the values under the radical sign are the same. For example:
\[ \sqrt{3} + 2\sqrt{3} = 3\sqrt{3} \]
If the radicals are different, they cannot be combined in this way.
- Q5: How do you simplify the square root of a fraction?
A: To simplify the square root of a fraction, apply the square root to the numerator and the denominator separately. For example:
\[ \sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4} \]
- Q6: Can square roots be simplified further if they include both numbers and variables?
A: Yes, both numbers and variables can be simplified together. For instance, simplify \(\sqrt{50x^2}\):
\[ \sqrt{50x^2} = \sqrt{25 \times 2 \times x^2} = 5x\sqrt{2} \]
Conclusion and Further Resources
In conclusion, simplifying square roots is a fundamental skill in mathematics that can be applied to a variety of problems. Understanding the principles behind simplifying square roots, such as factoring numbers into their prime components and recognizing perfect squares, allows for a deeper comprehension of mathematical concepts and more efficient problem-solving strategies.
Here are some key takeaways from this guide:
- Simplifying square roots involves breaking down the radicand into its prime factors and identifying perfect squares.
- Using the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) helps in separating and simplifying the factors of the radicand.
- Recognizing and utilizing the largest perfect square factor can significantly simplify the process.
- For variables under a square root, understanding how to handle even and odd exponents is crucial for simplification.
For those looking to further their understanding and practice their skills, here are some excellent resources:
By continuing to practice and explore these resources, you can master the art of simplifying square roots and apply this knowledge to more advanced mathematical concepts.
Đơn giản hóa căn bậc hai | Toán học với Mr. J
READ MORE:
Đơn giản hóa căn bậc hai dễ dàng (10 ví dụ)