Topic square root of 2 and 3: The square root of 2 and 3 are fascinating irrational numbers with profound implications in mathematics, geometry, and engineering. Discover their unique properties, historical significance, and practical applications that make them essential concepts in various fields of science and everyday life.
Table of Content
- Square Root of 2 and 3
- Introduction to Square Roots
- Mathematical Definition and Properties
- Historical Context and Significance
- Calculation Methods for Square Root of 2
- Properties of Square Root of 2
- Applications of Square Root of 2
- Calculation Methods for Square Root of 3
- Properties of Square Root of 3
- Applications of Square Root of 3
- Comparison of Square Root of 2 and 3
- Advanced Topics and Further Reading
- YOUTUBE: Khám phá giá trị và ý nghĩa của căn bậc hai của 2 trong video 'Root 2 - Numberphile'. Video này cung cấp cái nhìn sâu sắc về số vô tỷ nổi tiếng này.
Square Root of 2 and 3
The square roots of 2 and 3 are fundamental mathematical constants that have significant importance in various fields of science, mathematics, and engineering. Below is a detailed exploration of these two irrational numbers.
Square Root of 2
The square root of 2, denoted as \( \sqrt{2} \), is the positive number that, when multiplied by itself, gives the number 2. It is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal representation is non-repeating and non-terminating.
Mathematically,
\[ \sqrt{2} \approx 1.4142135623730950488 \ldots \]
This number is also known as Pythagoras' constant, as it is the length of the hypotenuse of a right-angled triangle with legs of length 1. It was the first number proven to be irrational.
Properties of \( \sqrt{2} \)
- Irrational number
- Non-repeating decimal
- Important in geometry, particularly in the context of right triangles
Square Root of 3
The square root of 3, denoted as \( \sqrt{3} \), is the positive number that, when multiplied by itself, gives the number 3. Like \( \sqrt{2} \), it is also an irrational number with a non-repeating and non-terminating decimal expansion.
Mathematically,
\[ \sqrt{3} \approx 1.7320508075688772935 \ldots \]
The square root of 3 appears frequently in geometry, especially in the context of equilateral triangles, where it represents the height when the side length is 2.
Properties of \( \sqrt{3} \)
- Significant in trigonometry and geometry, particularly with equilateral triangles
Applications
Both \( \sqrt{2} \) and \( \sqrt{3} \) have various applications:
- Geometry: Used in calculating distances and constructing geometric shapes.
- Engineering: Essential in design and analysis, especially in structural engineering.
- Physics: Appear in various physical formulas and constants.
- Mathematics: Fundamental in number theory and real analysis.
| Number | Decimal Approximation | Properties |
| \( \sqrt{2} \) | 1.4142135623730950488... | Irrational, non-repeating, used in right triangles |
| \( \sqrt{3} \) | 1.7320508075688772935... | Irrational, non-repeating, used in equilateral triangles |

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations that are essential in various fields, from basic arithmetic to advanced science and engineering. The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). This is represented as \( \sqrt{x} \). For example, the square root of 4 is 2, because \( 2 \times 2 = 4 \).
Square roots can be categorized into rational and irrational numbers. Rational square roots result in whole numbers or fractions, while irrational square roots have non-repeating, non-terminating decimal expansions.
Let's explore the square roots of 2 and 3, two significant irrational numbers:
- Square Root of 2 (\( \sqrt{2} \)): This is approximately 1.414213562373095 and is known for its role in the Pythagorean theorem, where it represents the length of the hypotenuse in a right triangle with legs of 1 unit each.
- Square Root of 3 (\( \sqrt{3} \)): This is approximately 1.732050807568877 and is important in geometry, particularly in the context of equilateral triangles, where it represents the height when the side length is 2 units.
The calculation of square roots can be performed using various methods, including:
- Prime Factorization: Breaking down a number into its prime factors to simplify the square root calculation for perfect squares.
- Long Division Method: A manual method to find square roots, particularly useful for non-perfect squares.
- Approximation Methods: Using iterative algorithms such as the Newton-Raphson method to find approximate values of square roots.
Understanding square roots is crucial as they are widely used in different mathematical contexts, including solving quadratic equations, analyzing geometric shapes, and in various scientific calculations.
Mathematical Definition and Properties
Square roots are mathematical operations that find a number which, when multiplied by itself, equals the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \). Here, we focus on the square roots of 2 and 3, which are both irrational numbers.
Square Root of 2 (\( \sqrt{2} \))
The square root of 2 is the positive number that satisfies the equation:
\[ \sqrt{2} \times \sqrt{2} = 2 \]
Since \( \sqrt{2} \) is irrational, its decimal representation is non-terminating and non-repeating:
\[ \sqrt{2} \approx 1.4142135623730950488 \ldots \]
Properties of \( \sqrt{2} \)
- It is an irrational number, meaning it cannot be expressed as a fraction of two integers.
- Its decimal expansion goes on forever without repeating.
- It is crucial in geometry, particularly in the context of right-angled triangles.
Square Root of 3 (\( \sqrt{3} \))
The square root of 3 is the positive number that satisfies the equation:
\[ \sqrt{3} \times \sqrt{3} = 3 \]
Like \( \sqrt{2} \), \( \sqrt{3} \) is also irrational, with a decimal representation that is non-terminating and non-repeating:
\[ \sqrt{3} \approx 1.7320508075688772935 \ldots \]
Properties of \( \sqrt{3} \)
- It is an irrational number with an infinite and non-repeating decimal expansion.
- It frequently appears in geometry, especially in equilateral triangles.
Comparative Properties
| Number | Decimal Approximation | Properties |
| \( \sqrt{2} \) | 1.4142135623730950488... | Irrational, non-repeating, used in right-angled triangles |
| \( \sqrt{3} \) | 1.7320508075688772935... | Irrational, non-repeating, used in equilateral triangles |
Understanding the mathematical definitions and properties of \( \sqrt{2} \) and \( \sqrt{3} \) provides a foundation for their applications in various mathematical and scientific contexts.
Historical Context and Significance
The discovery and understanding of square roots, particularly those of 2 and 3, have played crucial roles in the development of mathematics throughout history. These numbers have not only influenced mathematical theory but also practical applications in various fields.
Square Root of 2
The square root of 2, often referred to as the first known irrational number, has a rich historical context:
- Ancient Greece: The Greek mathematician Hippasus is credited with the discovery of the irrationality of \( \sqrt{2} \). This revelation was significant because it challenged the Greek belief that all numbers were rational. According to legend, this discovery was so controversial that Hippasus was reportedly executed for his findings.
- Pythagorean Theorem: \( \sqrt{2} \) emerges naturally in the context of the Pythagorean theorem, which states that the hypotenuse of a right-angled triangle with legs of length 1 is \( \sqrt{2} \). This relationship was crucial in the development of geometry.
- Symbolism: The symbol \( \sqrt{} \) for square roots was introduced by the German mathematician Christoff Rudolff in 1525. This notation has since become standard in mathematics.
Square Root of 3
The square root of 3 also holds historical significance, particularly in the realm of geometry and architecture:
- Ancient Civilizations: The value of \( \sqrt{3} \) was known to ancient civilizations, including the Egyptians and Indians, who used it in architectural designs and astronomical calculations. The ancient Indian mathematician Aryabhata provided an accurate approximation of \( \sqrt{3} \) in the 5th century.
- Geometric Applications: \( \sqrt{3} \) appears in the height of equilateral triangles, making it essential in various geometric constructions and proofs.
- Modern Usage: In modern times, \( \sqrt{3} \) is widely used in trigonometry, particularly in the study of 30-60-90 triangles, which have sides in the ratio 1 : \( \sqrt{3} \) : 2.
Impact on Mathematics
The discoveries of the irrationality of \( \sqrt{2} \) and \( \sqrt{3} \) have had profound impacts on mathematics:
- Development of Real Numbers: The realization that not all numbers are rational led to the development of the real number system, which includes both rational and irrational numbers.
- Advancements in Algebra: Understanding the properties of square roots and irrational numbers has advanced the field of algebra, influencing how equations and functions are studied and solved.
- Geometric Insights: The geometric significance of these square roots has contributed to advancements in Euclidean and non-Euclidean geometry, impacting both theoretical and applied mathematics.
The historical context and significance of the square roots of 2 and 3 highlight their foundational role in the evolution of mathematical thought and their enduring relevance in various scientific and engineering applications.
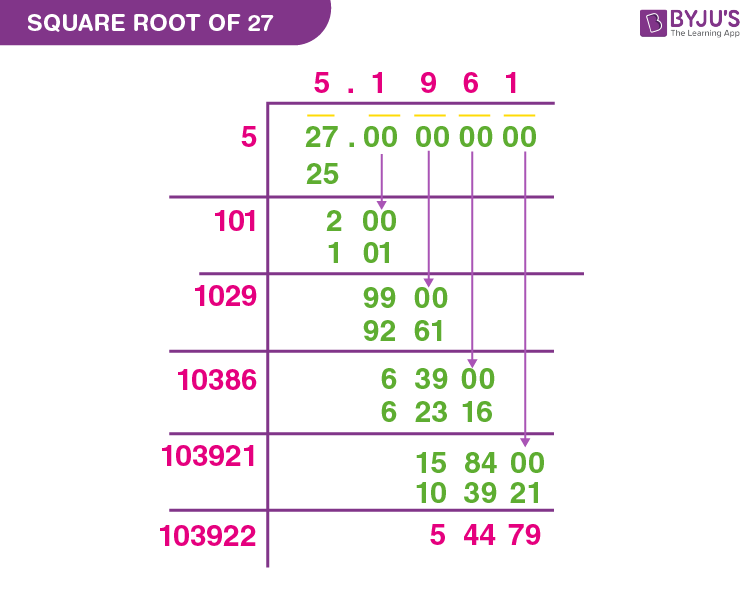
Calculation Methods for Square Root of 2
The square root of 2 (\( \sqrt{2} \)) is an irrational number, meaning its exact value cannot be represented as a simple fraction. However, various methods can be used to approximate its value with high precision. Here, we explore some of the most common calculation methods for \( \sqrt{2} \).
1. Long Division Method
The long division method is a manual process that provides a systematic way to find the square root of a number. It is particularly useful for finding square roots of non-perfect squares.
- Step 1: Write the number (2) and group the digits in pairs from the decimal point.
- Step 2: Find the largest number whose square is less than or equal to the first group (1 in this case).
- Step 3: Subtract the square of this number from the first group and bring down the next pair of digits.
- Step 4: Double the current quotient (1 in this case) and use it as a divisor. Find the largest digit to append to the divisor and quotient such that the product is less than or equal to the current dividend.
- Step 5: Repeat the process for the desired number of decimal places.
This method, though tedious, provides a step-by-step approach to approximating \( \sqrt{2} \).
2. Newton-Raphson Method
The Newton-Raphson method is an iterative numerical technique used to find successively better approximations to the roots of a real-valued function. For square roots, the method can be applied as follows:
- Step 1: Start with an initial guess \( x_0 \) (e.g., \( x_0 = 1 \)).
- Step 2: Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{2}{x_n} \right) \).
- Step 3: Repeat the process until the difference between successive approximations is within a desired tolerance level.
The Newton-Raphson method converges very quickly and is efficient for calculating \( \sqrt{2} \).
3. Babylonian Method (Heron's Method)
The Babylonian method, also known as Heron's method, is an ancient algorithm for finding square roots that is remarkably similar to the Newton-Raphson method:
- Step 1: Start with an initial guess \( x_0 \) (e.g., \( x_0 = 1 \)).
- Step 2: Compute the next approximation using \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{2}{x_n} \right) \).
- Step 3: Continue the iteration until the result stabilizes to a desired accuracy.
This method is known for its simplicity and effectiveness.
4. Continued Fractions
The square root of 2 can also be expressed as a continued fraction, which provides a way to represent the number through an infinite sequence:
\[ \sqrt{2} = 1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \cdots}}} \]
This representation, while less practical for direct computation, highlights the irrational nature of \( \sqrt{2} \) and provides insights into its structure.
Comparison of Methods
| Method | Accuracy | Complexity | Comments |
| Long Division | High | Manual and tedious | Good for understanding basic principles |
| Newton-Raphson | Very High | Iterative and fast | Widely used in computational methods |
| Babylonian | High | Simple and effective | Similar to Newton-Raphson |
| Continued Fractions | Variable | Theoretical | Provides insights into the nature of \( \sqrt{2} \) |
Each method for calculating the square root of 2 offers unique insights and varying levels of complexity and accuracy. Choosing the right method depends on the context and the desired precision.

Properties of Square Root of 2
The square root of 2, denoted as \( \sqrt{2} \), is a unique and important number in mathematics. As an irrational number, it has several interesting and significant properties that have implications in various fields of study. Below, we explore these properties in detail.
Irrationality
The square root of 2 is an irrational number, which means it cannot be expressed as a fraction of two integers. Its decimal representation is non-terminating and non-repeating:
\[ \sqrt{2} \approx 1.4142135623730950488 \ldots \]
This property was historically significant as its discovery challenged the ancient Greek belief that all numbers were rational.
Geometric Significance
In geometry, \( \sqrt{2} \) often appears in the context of right-angled triangles. For a right-angled triangle with both legs of length 1, the length of the hypotenuse is \( \sqrt{2} \). This relationship can be derived from the Pythagorean theorem:
\[ \text{Hypotenuse}^2 = 1^2 + 1^2 = 2 \implies \text{Hypotenuse} = \sqrt{2} \]
Algebraic Properties
- \( (\sqrt{2})^2 = 2 \): Multiplying \( \sqrt{2} \) by itself gives the number 2.
- \( \frac{1}{\sqrt{2}} = \sqrt{\frac{1}{2}} \): The reciprocal of \( \sqrt{2} \) is \( \sqrt{\frac{1}{2}} \), which simplifies to \( \frac{\sqrt{2}}{2} \).
- \( \sqrt{2} \) is a solution to the equation \( x^2 = 2 \).
Decimal Expansion
The decimal expansion of \( \sqrt{2} \) is infinite and does not repeat, reflecting its irrational nature. Despite this, the first few digits are:
\[ 1.4142135623730950488 \ldots \]
Continued Fraction Representation
The square root of 2 can also be represented as a continued fraction, which provides a unique way to express the number through an infinite sequence:
\[ \sqrt{2} = 1 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \cdots}}} \]
This representation, while not practical for computation, highlights the complex and infinite nature of \( \sqrt{2} \).
Applications
The properties of \( \sqrt{2} \) make it essential in various applications, including:
- Geometry: Used in the calculation of distances, particularly in right-angled triangles and polygons.
- Algebra: Appears in solutions to quadratic equations and other algebraic expressions.
- Trigonometry: Integral in defining trigonometric functions and identities.
- Engineering: Used in design and analysis, especially where precise measurements and calculations are required.
- Physics: Appears in formulas and constants, contributing to the understanding of physical phenomena.
Historical Context
The discovery of the irrationality of \( \sqrt{2} \) is attributed to the Greek mathematician Hippasus, a member of the Pythagorean school. This discovery was revolutionary at the time and marked a significant milestone in the history of mathematics.
The square root of 2 is a number with deep mathematical roots and extensive applications. Its properties continue to be studied and utilized across various scientific and engineering disciplines, underscoring its enduring significance.
Applications of Square Root of 2
The square root of 2, often denoted as √2, has numerous applications across various fields. Below are some key applications:
1. Geometry
In geometry, the square root of 2 appears in several contexts:
- Diagonal of a Square: The length of the diagonal of a square with side length 1 is √2. This comes from the Pythagorean theorem where the diagonal (d) of a square is given by \(d = \sqrt{a^2 + a^2} = \sqrt{2a^2} = a\sqrt{2}\), where \(a\) is the side length.
- Regular Octagon: The distance between opposite sides of a regular octagon inscribed in a unit circle is √2.
2. Trigonometry
In trigonometry, √2 appears in various trigonometric functions and identities:
- 45° Angle: The sine and cosine of 45° (or π/4 radians) are both equal to \(\frac{\sqrt{2}}{2}\).
- Roots of Unity: √2 appears in the context of complex numbers and the calculation of roots of unity.
3. Physics
In physics, √2 is significant in wave mechanics and quantum physics:
- Wave Equations: √2 appears in solutions to certain wave equations, particularly in the normalization of wave functions.
- Quantum Mechanics: The probability amplitudes in quantum mechanics often involve √2, especially in systems with symmetrical properties.
4. Engineering
In engineering, √2 is used in various design and analysis contexts:
- Signal Processing: In digital signal processing, the √2 factor is used in algorithms for computing the Fast Fourier Transform (FFT).
- Electrical Engineering: √2 is used in the calculation of RMS (Root Mean Square) values for alternating current (AC) signals.
5. Art and Architecture
√2 is also seen in art and architecture, especially in design and proportion:
- Aesthetic Proportions: The √2 ratio, also known as the silver ratio, is used in designing aesthetically pleasing rectangles and other shapes.
- Paper Sizes: The international paper size standard (ISO 216) uses the aspect ratio of 1:√2, ensuring that a page folded in half retains the same proportions.
Calculation Methods for Square Root of 3
The square root of 3, approximately 1.732, is an irrational number. Calculating it can be done using several methods:
1. Long Division Method
- Pair the digits of the number from right to left, placing a decimal point above the bar once all digits are paired.
- Find the largest number whose square is less than or equal to the first pair. This number is the first digit of the square root.
- Subtract the square of this number from the first pair and bring down the next pair of digits.
- Double the number already found and use it as a new divisor, leaving a space for the next digit of the root.
- Determine the largest digit for the new divisor such that its product with the entire new divisor does not exceed the current number.
- Repeat the process for more decimal places.
2. Prime Factorization Method
This method is not practical for finding the square root of 3 because 3 is a prime number and does not have perfect square factors. However, it is useful for numbers that can be broken down into pairs of prime factors.
3. Estimation Method
Use this method for quick approximations:
- Find the nearest perfect squares around 3. For example, 1 and 4.
- Estimate the square root by averaging or using a proportion. Since 3 is closer to 4 than to 1, the square root of 3 is closer to 2 than to 1.
- Refine your estimate using iterative methods or a calculator.
4. Newton's Method (Iterative Method)
Newton's method provides a rapid approximation:
- Choose an initial guess (x0), for example, 1.7.
- Use the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{3}{x_n} \right) \).
- Repeat the iteration until the desired precision is achieved.
Example Calculation Using Long Division
| Step | Operation | Result |
| 1 | 1.732 | 1.732 x 1.732 = 2.999824 ≈ 3 |
| 2 | 2 | New divisor: 34 (2X + X), next step 34 x 0.7 = 23.8 |
By following these steps and methods, one can approximate the square root of 3 to the desired degree of accuracy.
Properties of Square Root of 3
The square root of 3, denoted as \( \sqrt{3} \), has several important properties in mathematics. Below are some of the key properties:
- Irrational Number: The square root of 3 is an irrational number, which means it cannot be expressed as a simple fraction and its decimal expansion is non-terminating and non-repeating. The approximate value is \( \sqrt{3} \approx 1.732 \).
- Exponential Form: The square root of 3 can be expressed in exponential form as \( 3^{1/2} \) or \( 3^{0.5} \).
- Multiplication Property: The product of the square roots of two numbers is equal to the square root of the product of those numbers. For example, \( \sqrt{a} \times \sqrt{b} = \sqrt{a \times b} \). Specifically, \( \sqrt{3} \times \sqrt{3} = \sqrt{9} = 3 \).
- Addition Property: The square root of a sum is not equal to the sum of the square roots. In general, \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \).
- Square of Square Root: The square of \( \sqrt{3} \) returns the original number, i.e., \( (\sqrt{3})^2 = 3 \).
- Even and Odd Digits: The square root of a number with an even number of digits is not necessarily an integer, but if the number of digits is odd, the square root will not be an integer. For example, 3 has one digit, and its square root is irrational.
- Prime Factorization: Since 3 is a prime number, its square root cannot be simplified further into smaller integer components.
- Application in Geometry: The square root of 3 frequently appears in geometric calculations, especially involving equilateral triangles where the height can be expressed as \( \frac{\sqrt{3}}{2} \) times the side length.
- Complex Numbers: The square root of a negative number involving 3 is expressed in terms of imaginary numbers. For example, \( \sqrt{-3} = i\sqrt{3} \), where \( i \) is the imaginary unit \( i = \sqrt{-1} \).
Applications of Square Root of 3
The square root of 3 (\(\sqrt{3}\)) has numerous practical applications across various fields such as geometry, trigonometry, engineering, and more. Here are some key areas where \(\sqrt{3}\) is utilized:
- Geometry and Trigonometry
The height of an equilateral triangle with side length 2 is \(\sqrt{3}\). Additionally, in a 30-60-90 triangle with a hypotenuse of 2, the longer leg is \(\sqrt{3}\). This constant also appears as the space diagonal of a unit cube.
- Electrical Engineering
In three-phase electrical systems, the voltage between two phases is \(\sqrt{3}\) times the line to neutral voltage. This relationship is crucial for designing and analyzing power systems.
- Power Engineering
The square root of 3 is essential in calculating the voltage in three-phase power systems. This allows for efficient transmission and distribution of electricity.
- Computer Graphics
In computer graphics, \(\sqrt{3}\) is used to calculate distances and angles between points in 2D and 3D spaces, improving the accuracy and realism of rendered images.
- Navigation
\(\sqrt{3}\) helps in navigation, particularly in calculating the distance between two points on a plane or globe, aiding in accurate mapping and route planning.
- Cryptography
Square roots, including \(\sqrt{3}\), are employed in cryptographic algorithms for secure data transmission, ensuring privacy and data integrity.
These applications highlight the versatility and importance of the square root of 3 in both theoretical and practical contexts, contributing to advancements in technology, engineering, and mathematics.
Comparison of Square Root of 2 and 3
Comparing the square roots of 2 and 3 involves understanding their values, properties, and applications in various fields. Both square roots are irrational numbers, meaning they cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions.
- Approximate Values:
- \(\sqrt{2} \approx 1.414\)
- \(\sqrt{3} \approx 1.732\)
- Mathematical Properties:
- Irrationality: Both numbers are irrational and their decimal representations are non-repeating and infinite.
- Square Property: For any number \( x \), \( x = \sqrt{2} \) and \( x = \sqrt{3} \) are the solutions to \( x^2 = 2 \) and \( x^2 = 3 \), respectively.
- Comparison by Squaring: One way to compare \(\sqrt{2}\) and \(\sqrt{3}\) is by squaring them:
- \((\sqrt{2})^2 = 2\)
- \((\sqrt{3})^2 = 3\)
- Since \(2 < 3\), it follows that \(\sqrt{2} < \sqrt{3}\).
- Geometric Interpretation: In geometry, the square root of a number can represent the length of the diagonal of a square with sides of a given length:
- The diagonal of a square with side length 1 is \(\sqrt{2}\).
- The diagonal of a square with side length \(\sqrt{3}\) is \(\sqrt{3}\).
- Applications:
- Square Root of 2:
- Used in calculations involving right triangles, especially in the context of the Pythagorean theorem.
- Common in geometry and trigonometry, particularly in deriving the lengths of diagonals in squares.
- Square Root of 3:
- Used in engineering and physics, especially in problems involving equilateral triangles.
- Important in the study of hexagonal structures and tiling.
- Square Root of 2:
Overall, while both \(\sqrt{2}\) and \(\sqrt{3}\) play crucial roles in various mathematical and real-world applications, \(\sqrt{3}\) is larger than \(\sqrt{2}\). Their unique properties and values make them fundamental constants in many scientific and engineering calculations.
Advanced Topics and Further Reading
The study of square roots, particularly those of non-perfect squares like 2 and 3, extends into various advanced mathematical topics. Below are some key areas and suggestions for further reading:
- Continued Fractions: The square roots of 2 and 3 can be expressed as infinite continued fractions, which provide deep insights into their properties and are useful in number theory. The continued fraction for √2 is [1; 2, 2, 2, ...] and for √3 is [1; 1, 2, 1, 2, 1, 2, ...].
- Diophantine Equations: These equations involve finding integer solutions to polynomial equations. The Pell's equation, x² - 2y² = 1, is closely related to √2 and has a rich history in mathematics.
- Algebraic Number Theory: √2 and √3 are examples of quadratic irrationals. Studying these numbers leads to the exploration of algebraic integers and fields, expanding the understanding of number systems.
- Complex Analysis: The exploration of square roots extends into the complex plane, where the square roots of complex numbers are studied. This topic is crucial for understanding the behavior of functions in complex analysis.
- Geometry: In geometry, √2 and √3 are fundamental in the study of shapes and their properties. The diagonal of a unit square is √2, and the height of an equilateral triangle with unit side length is √3. These constants appear in various geometric constructions and proofs.
- Computational Methods: There are advanced algorithms for computing square roots to high precision, including the Newton-Raphson method and the use of iterative methods in computer science and numerical analysis.
For further reading, consider the following topics:
- Exploring the properties of quadratic irrationals in "Algebraic Number Theory".
- Understanding continued fractions and their applications in "Number Theory".
- Studying Pell's equations and their solutions in "Diophantine Equations".
- Learning about the complex plane and the roots of complex numbers in "Complex Analysis".
- Investigating geometric properties involving square roots in "Euclidean Geometry".
- Delving into computational techniques for precise calculations in "Numerical Analysis".
These topics not only provide a deeper understanding of the mathematical significance of square roots but also highlight their applications across different fields of study.
Khám phá giá trị và ý nghĩa của căn bậc hai của 2 trong video 'Root 2 - Numberphile'. Video này cung cấp cái nhìn sâu sắc về số vô tỷ nổi tiếng này.
Root 2 - Numberphile
READ MORE:
Khám phá giá trị và ý nghĩa của căn bậc hai của 2 trong video 'Căn Bậc Hai của 2'. Video này cung cấp cái nhìn sâu sắc về số vô tỷ nổi tiếng này.
Căn Bậc Hai của 2