Topic square root of 2 divided by 2: The expression "square root of 2 divided by 2" holds significant value in mathematics, geometry, and trigonometry. This article explores its mathematical definition, geometric interpretations, and wide-ranging applications in fields like engineering, physics, and computer graphics, offering a comprehensive understanding of why this expression is so essential.
Table of Content
- Understanding the Division of Square Root of 2 by 2
- Introduction
- Mathematical Definition
- Decimal Approximation
- 45°-45°-90° Triangle
- Unit Circle Representation
- Sine and Cosine of 45°
- Engineering Applications
- Physics Applications
- Computer Graphics Applications
- YOUTUBE: Video giải thích cách tính căn bậc hai của 2 chia cho 2 một cách hài hước, giúp người xem dễ hiểu và thú vị hơn về khái niệm toán học này.
Understanding the Division of Square Root of 2 by 2
The expression \(\frac{\sqrt{2}}{2}\) is a mathematical concept that can be useful in various applications, particularly in trigonometry and geometry. Here we explore the details and implications of this expression.
Mathematical Expression
The expression can be written as:
\[\frac{\sqrt{2}}{2}\]
Decimal Form
When calculated, the value of \(\frac{\sqrt{2}}{2}\) in decimal form is approximately:
\[ \frac{\sqrt{2}}{2} \approx 0.7071 \]
Geometric Interpretation
In geometry, the expression \(\frac{\sqrt{2}}{2}\) often appears in relation to right triangles and unit circles:
- In a 45°-45°-90° triangle, the length of the legs are equal and the hypotenuse is
\(\sqrt{2}\)times the length of a leg. Thus, each leg is\(\frac{\sqrt{2}}{2}\)times the hypotenuse. - In the unit circle, the coordinates of a point at a 45° angle (or π/4 radians) from the x-axis are
\(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)\).
Trigonometric Functions
The expression \(\frac{\sqrt{2}}{2}\) frequently appears in trigonometric functions:
- It is the sine and cosine of 45° (or π/4 radians):
\[ \sin\left(\frac{\pi}{4}\right) = \cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} \]
Applications
The value \(\frac{\sqrt{2}}{2}\) is commonly used in various fields:
- Engineering: Used in signal processing and control systems where sine and cosine functions are critical.
- Physics: Appears in wave mechanics and quantum physics calculations.
- Computer Graphics: Utilized in rotations and transformations within graphical simulations and modeling.
Conclusion
The expression \(\frac{\sqrt{2}}{2}\) is a significant mathematical value with wide-ranging applications. Understanding its properties and uses is essential for students and professionals in science, technology, engineering, and mathematics (STEM) fields.
READ MORE:
Introduction
The expression \(\frac{\sqrt{2}}{2}\) is a fundamental concept in mathematics that appears frequently in various fields such as geometry, trigonometry, and physics. This value is derived from the division of the square root of 2 by 2, resulting in an important irrational number approximately equal to 0.7071. Here, we delve into its definition, significance, and applications.
Let's break down the understanding of this expression step by step:
- Mathematical Definition: The expression
\(\frac{\sqrt{2}}{2}\)is a ratio that simplifies to a precise value, crucial for various mathematical calculations. - Decimal Approximation: Numerically,
\(\frac{\sqrt{2}}{2} \approx 0.7071\), which is used in practical computations. - Geometric Significance: This value often appears in geometric contexts, such as in right-angled triangles and the unit circle.
- Trigonometric Relevance: In trigonometry,
\(\frac{\sqrt{2}}{2}\)is the sine and cosine of a 45° (or π/4 radians) angle, making it pivotal in trigonometric identities and equations. - Applications: Understanding
\(\frac{\sqrt{2}}{2}\)is essential in various fields:- Engineering: Used in signal processing and control systems.
- Physics: Important in wave mechanics and quantum physics.
- Computer Graphics: Utilized in rotations and transformations within graphical simulations.
This comprehensive guide will further explore these aspects, providing a deeper insight into the significance of the square root of 2 divided by 2.
Mathematical Definition
The expression \(\frac{\sqrt{2}}{2}\) is derived from the square root of 2, which is an irrational number approximately equal to 1.414213562. When divided by 2, it results in another irrational number. This value is significant in various mathematical contexts and can be expressed as:
\[\frac{\sqrt{2}}{2} = \frac{1.414213562}{2} \approx 0.7071\]
Let's break down this concept further:
- Square Root of 2: The square root of 2, denoted as \(\sqrt{2}\), is the positive algebraic number that, when multiplied by itself, equals 2. It is an important constant in mathematics, often appearing in geometry and algebra.
- Division by 2: By dividing \(\sqrt{2}\) by 2, we obtain the expression \(\frac{\sqrt{2}}{2}\). This operation scales the value of \(\sqrt{2}\) down by a factor of 2, resulting in approximately 0.7071.
- Irrational Number: Both \(\sqrt{2}\) and \(\frac{\sqrt{2}}{2}\) are irrational numbers, meaning they cannot be expressed as a simple fraction of two integers. Their decimal representations are non-terminating and non-repeating.
In summary, the mathematical definition of \(\frac{\sqrt{2}}{2}\) is a straightforward yet profound expression that is crucial in various mathematical calculations and theories. It simplifies many trigonometric functions and geometric problems, making it an essential part of mathematical studies.
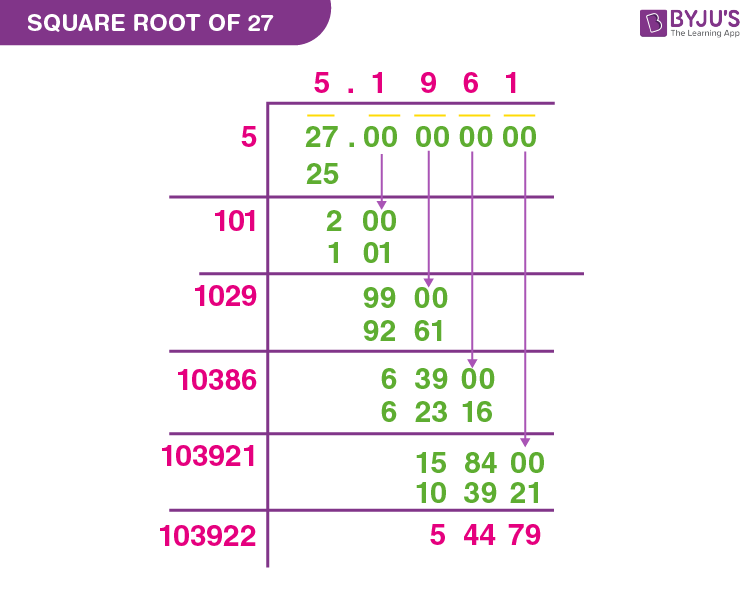
Decimal Approximation
The decimal approximation of the expression \(\frac{\sqrt{2}}{2}\) provides a practical way to work with this irrational number in everyday calculations. The process of finding this approximation can be detailed as follows:
- Calculate the Square Root of 2: The square root of 2 (\(\sqrt{2}\)) is an irrational number approximately equal to 1.414213562.
- Divide by 2: To find \(\frac{\sqrt{2}}{2}\), we divide 1.414213562 by 2, which yields approximately 0.707106781.
- Decimal Representation: Thus, the decimal approximation of \(\frac{\sqrt{2}}{2}\) is:
- Precision: The decimal approximation can be extended to more digits for greater precision, commonly used in scientific calculations. For example, \(\frac{\sqrt{2}}{2} \approx 0.7071067811865476\).
\[\frac{\sqrt{2}}{2} \approx 0.7071\]
This decimal approximation is highly useful in various fields, such as engineering, physics, and computer graphics, where precise calculations are necessary. While the exact value of \(\frac{\sqrt{2}}{2}\) is irrational and cannot be fully expressed as a decimal, the approximation \(\approx 0.7071\) provides a practical and manageable form for real-world applications.
45°-45°-90° Triangle
The 45°-45°-90° triangle, also known as an isosceles right triangle, has unique properties that make it an essential concept in geometry. This triangle has two equal angles of 45 degrees and a right angle of 90 degrees. Let's explore its characteristics in detail:
- Equal Legs:
In a 45°-45°-90° triangle, the two legs are of equal length. If we denote the length of each leg as \(a\), then both legs are \(a\).
- Hypotenuse:
The hypotenuse (the side opposite the right angle) is \(\sqrt{2}\) times the length of each leg. This relationship can be derived using the Pythagorean theorem:
\[ \text{Hypotenuse} = \sqrt{a^2 + a^2} = \sqrt{2a^2} = a\sqrt{2} \]
- Normalized Lengths:
If the length of each leg is normalized to 1, the hypotenuse becomes \(\sqrt{2}\). Thus, each leg in a unit 45°-45°-90° triangle can be expressed as:
\[ \text{Leg Length} = \frac{\text{Hypotenuse}}{\sqrt{2}} = \frac{\sqrt{2}}{\sqrt{2}} = 1 \]
In cases where the hypotenuse is set to 2, the legs will be:
\[ \text{Leg Length} = \frac{2}{\sqrt{2}} = \sqrt{2} \]
Therefore, each leg can also be expressed as:
\[ \text{Leg Length} = \frac{\sqrt{2}}{2} \]
- Geometric Applications:
Trigonometry: The 45°-45°-90° triangle is crucial in trigonometry, where the sine and cosine of a 45° angle are both \(\frac{\sqrt{2}}{2}\). This is because:
\[ \sin(45^\circ) = \cos(45^\circ) = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
Geometry: This triangle is used in geometric constructions and proofs, particularly in problems involving symmetry and equal partitioning of angles.
The 45°-45°-90° triangle, with its unique properties and simple ratio relationships, serves as a fundamental building block in both theoretical and applied mathematics. Understanding its dimensions and relationships is essential for solving various geometric and trigonometric problems.

Unit Circle Representation
The unit circle is a fundamental concept in trigonometry, representing a circle with a radius of one centered at the origin of the coordinate plane. The expression \(\frac{\sqrt{2}}{2}\) plays a significant role in the unit circle, especially at the 45° (or \(\frac{\pi}{4}\) radians) angle. Here’s a detailed step-by-step breakdown of its representation:
- Definition of the Unit Circle:
The unit circle is defined by the equation:
\[ x^2 + y^2 = 1 \]
where \(x\) and \(y\) are the coordinates of any point on the circle.
- 45° (or \(\frac{\pi}{4}\) radians) Angle:
At a 45° angle, the coordinates of the point on the unit circle are equal due to the symmetry of the angle. These coordinates are:
\[ \left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) \]
- Trigonometric Functions:
For the angle of 45°, the sine and cosine values are both \(\frac{\sqrt{2}}{2}\). This can be expressed as:
\[ \sin\left(\frac{\pi}{4}\right) = \cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} \]
- Verification:
To verify these coordinates satisfy the unit circle equation, substitute \(x\) and \(y\) with \(\frac{\sqrt{2}}{2}\):
\[ \left( \frac{\sqrt{2}}{2} \right)^2 + \left( \frac{\sqrt{2}}{2} \right)^2 = \frac{2}{4} + \frac{2}{4} = \frac{4}{4} = 1 \]
- Geometric Significance:
The coordinates \(\left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) divide the unit circle into equal 45° segments, showcasing the symmetry and uniformity in the circle.
- In rotations and reflections, these points are critical for maintaining consistent transformations.
- In trigonometric identities and equations, these values simplify calculations and provide clear geometric interpretations.
Understanding the unit circle representation of \(\frac{\sqrt{2}}{2}\) provides valuable insight into trigonometric functions and their geometric applications. This foundational concept is pivotal in advanced mathematics, physics, and engineering disciplines.
Sine and Cosine of 45°
Understanding the sine and cosine of 45° is crucial in trigonometry. The angle of 45° is significant because it divides the first quadrant of the unit circle into two equal parts.
Value Calculation
For a 45° angle (or \( \frac{\pi}{4} \) radians), the values of sine and cosine can be determined using the properties of an isosceles right triangle (45°-45°-90° triangle).
- In a 45°-45°-90° triangle, the legs are equal, and the hypotenuse is \( \sqrt{2} \) times the length of a leg.
- If each leg has a length of 1, then the hypotenuse is \( \sqrt{2} \).
Using these properties, we calculate the sine and cosine as follows:
- Sine of 45°: The sine of an angle is the ratio of the length of the opposite side to the hypotenuse. Therefore, for 45°, \[ \sin(45°) = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}. \]
- Cosine of 45°: The cosine of an angle is the ratio of the length of the adjacent side to the hypotenuse. Thus, for 45°, \[ \cos(45°) = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}. \]
Unit Circle Representation
On the unit circle, the coordinates corresponding to a 45° angle are (\( \frac{\sqrt{2}}{2} \), \( \frac{\sqrt{2}}{2} \)). This representation can be visualized as follows:
- The x-coordinate (cosine) is \( \frac{\sqrt{2}}{2} \).
- The y-coordinate (sine) is \( \frac{\sqrt{2}}{2} \).
The unit circle shows that both sine and cosine values are equal at 45° and lie in the first quadrant, making an angle bisector through the line \( y = x \).
Significance in Trigonometric Functions
Knowing these values is essential for simplifying trigonometric expressions and solving equations. They are also foundational for understanding the behavior of waves and oscillations, which frequently occur in physics and engineering applications.
The values \( \frac{\sqrt{2}}{2} \) for both sine and cosine at 45° highlight the symmetry and fundamental relationships in trigonometry, aiding in the comprehension of more complex mathematical concepts.
Engineering Applications
The value of \(\frac{\sqrt{2}}{2}\) is prevalent in various engineering applications due to its occurrence in geometrical transformations and trigonometric calculations. Below are some of the key engineering applications where \(\frac{\sqrt{2}}{2}\) plays a significant role:
-
Structural Engineering:
In structural engineering, the value \(\frac{\sqrt{2}}{2}\) is often used in the analysis of forces and stress in components that are subjected to loads at 45-degree angles. For instance, the shear stress on a diagonal plane within a structural element can be calculated using trigonometric functions involving \(\frac{\sqrt{2}}{2}\).
-
Signal Processing:
In signal processing, the discrete Fourier transform (DFT) and its inverse are integral to analyzing and manipulating signals. The rotation of signal components in the complex plane, particularly at 45-degree angles, uses the value \(\frac{\sqrt{2}}{2}\) to determine the new magnitudes and phases of the signals.
-
Electrical Engineering:
In electrical engineering, particularly in the analysis of AC circuits, the phasor representation of voltages and currents often involves trigonometric calculations where the sine and cosine of 45 degrees, both equal to \(\frac{\sqrt{2}}{2}\), are used. This simplifies the calculations of power and impedance in these circuits.
-
Robotics and Automation:
In robotics, \(\frac{\sqrt{2}}{2}\) is used in the kinematic equations that describe the motion of robotic arms, especially those with joints that rotate at 45-degree angles. These equations help determine the precise positioning and orientation of the end-effector.
-
Computer Graphics:
In computer graphics, rotating objects and images often involves matrix transformations that use the value \(\frac{\sqrt{2}}{2}\). For example, a 45-degree rotation matrix includes \(\frac{\sqrt{2}}{2}\) to maintain the correct proportions and orientations of the objects being rotated.
These applications highlight the importance of the value \(\frac{\sqrt{2}}{2}\) in engineering, demonstrating how fundamental mathematical constants are utilized in practical and technological contexts to solve complex problems.
Physics Applications
The value of (approximately 0.707) finds extensive use in various physics applications due to its significance in normalizing wave functions, describing mean free paths, and representing probabilities in quantum mechanics.
- Quantum Mechanics: In quantum mechanics, the factor often appears in the normalization of wave functions. For example, the wavefunction of a neutral pion can be expressed using this factor to ensure the total probability sums to 1, crucial for accurate physical predictions.
- Mean Free Path: In statistical mechanics, the mean free path, which is the average distance a particle travels before colliding with another particle, is divided by . This adjustment accounts for the relative velocities of particles, improving the model's accuracy in describing real-world systems.
- Probability Amplitudes: The factor also appears in calculations involving probability amplitudes. For instance, in the superposition principle of quantum states, coefficients such as ensure that the probabilities derived from these amplitudes correctly sum to unity.
These applications demonstrate the importance of in maintaining the integrity and accuracy of physical models, ensuring they align with observable phenomena.

Computer Graphics Applications
The value of \( \frac{\sqrt{2}}{2} \) plays a crucial role in various aspects of computer graphics. Its significance stems from its relationship to fundamental geometric and trigonometric principles, which are heavily utilized in graphics computations.
- Vector Normalization:
In 2D and 3D graphics, vectors often need to be normalized, meaning they are scaled to have a unit length. When normalizing vectors, the length (or magnitude) of a vector is computed using the Pythagorean theorem, which involves square roots. For instance, a vector \( \mathbf{v} = (x, y) \) is normalized by dividing each component by the vector's magnitude \( \sqrt{x^2 + y^2} \). The value \( \frac{\sqrt{2}}{2} \) appears frequently when dealing with unit vectors in diagonal directions.
- Rotation and Transformation:
Rotating objects is a fundamental operation in graphics. The rotation matrix for a 45° angle involves the sine and cosine of 45°, both of which are \( \frac{\sqrt{2}}{2} \). This matrix is used to transform the coordinates of points in 2D space:
$$ R_{45^\circ} = \begin{pmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{pmatrix} $$
This transformation is essential in creating rotations in animations and other graphical manipulations.
- Pixel Shading and Lighting:
In pixel shading and lighting calculations, normal vectors are used to determine the angle of incidence of light on a surface. When these normals are at 45° angles, the components involve \( \frac{\sqrt{2}}{2} \). Accurate lighting models enhance the realism of rendered scenes.
- Distance Calculations:
Calculating the distance between two points in 2D or 3D space is a common task in computer graphics. The Euclidean distance formula, which includes square root calculations, frequently results in values that involve \( \frac{\sqrt{2}}{2} \), especially when dealing with unit distances and grids.
Overall, \( \frac{\sqrt{2}}{2} \) is a key value in the mathematical foundations of computer graphics, enabling precise and efficient computations in rendering, transformations, and more.
Video giải thích cách tính căn bậc hai của 2 chia cho 2 một cách hài hước, giúp người xem dễ hiểu và thú vị hơn về khái niệm toán học này.
Căn bậc hai của 2 chia cho 2 một cách hài hước