Topic proof square root of 2 is irrational: The proof that the square root of 2 is irrational is a fundamental concept in mathematics, demonstrating that not all numbers can be expressed as a ratio of two integers. This article explores various methods of proof, historical context, and the implications of this significant mathematical discovery.
Table of Content
- Proof that the Square Root of 2 is Irrational
- Introduction
- Understanding Rational and Irrational Numbers
- The Concept of Square Roots
- Assumption of Rationality
- Proof by Contradiction
- Squaring the Assumed Rational Expression
- Implications for Even and Odd Numbers
- Analyzing the Even Nature of \( a \)
- Substitution Back into the Equation
- Implications for \( b \)
- Identifying the Contradiction
- Conclusion of the Proof
- Significance and Applications of the Proof
- Historical Context and Development
- Common Misconceptions
- Further Reading and References
- YOUTUBE: Video này chứng minh rằng căn bậc hai của 2 là số vô tỉ, sử dụng phương pháp chứng minh phản chứng. Hãy khám phá sự thú vị của toán học!
Proof that the Square Root of 2 is Irrational
The proof that the square root of 2 is irrational is a classic example of a proof by contradiction. We assume the opposite of what we want to prove and show that this leads to a contradiction, hence proving the original statement.
Assumption
Assume that \( \sqrt{2} \) is rational. This means it can be expressed as a fraction of two integers \( \frac{a}{b} \) in simplest form (i.e., \( a \) and \( b \) are coprime, meaning they have no common factors other than 1).
Therefore, we can write:
\( \sqrt{2} = \frac{a}{b} \)
Square Both Sides
Square both sides of the equation to get rid of the square root:
\( 2 = \frac{a^2}{b^2} \)
Multiplying both sides by \( b^2 \) gives:
\( 2b^2 = a^2 \)
Analysis of the Equation
This equation \( 2b^2 = a^2 \) implies that \( a^2 \) is an even number (since it is 2 times some integer \( b^2 \)).
Conclusion for \( a \)
If \( a^2 \) is even, then \( a \) must also be even (since the square of an odd number is odd). Therefore, we can write \( a \) as:
\( a = 2k \)
for some integer \( k \).
Substitution and Further Analysis
Substitute \( a = 2k \) back into the original equation:
\( 2b^2 = (2k)^2 \)
which simplifies to:
\( 2b^2 = 4k^2 \)
Divide both sides by 2:
\( b^2 = 2k^2 \)
Conclusion for \( b \)
This equation \( b^2 = 2k^2 \) implies that \( b^2 \) is even, and hence \( b \) is also even.
Contradiction
We have shown that both \( a \) and \( b \) are even, which contradicts our initial assumption that \( \frac{a}{b} \) is in simplest form (since both \( a \) and \( b \) having a common factor of 2 means the fraction was not in simplest form).
Conclusion
Therefore, our assumption that \( \sqrt{2} \) is rational must be false. Thus, \( \sqrt{2} \) is irrational.

READ MORE:
Introduction
The proof that the square root of 2 is irrational is a fundamental result in mathematics. This proof shows that √2 cannot be expressed as a ratio of two integers, making it an irrational number. The proof typically employs a method known as proof by contradiction, where we assume the opposite of what we want to prove and show that this assumption leads to a logical inconsistency. This approach not only solidifies our understanding of irrational numbers but also showcases the elegance of mathematical reasoning.
- Assume that √2 is rational, meaning it can be written as a fraction
\(\frac{a}{b}\) , where\(a\) and\(b\) are integers with no common factors (i.e., the fraction is in its simplest form). - Square both sides of the equation
\(\sqrt{2} = \frac{a}{b}\) to get\(2 = \frac{a^2}{b^2}\) . - Multiply both sides by
\(b^2\) to obtain\(2b^2 = a^2\) . This implies that\(a^2\) is an even number since it is two times some integer\(b^2\) . - Since
\(a^2\) is even,\(a\) must also be even (only an even number squared results in an even number). Let\(a = 2k\) for some integer\(k\) . - Substitute
\(a = 2k\) back into the equation\(2b^2 = a^2\) to get\(2b^2 = (2k)^2 = 4k^2\) , simplifying to\(b^2 = 2k^2\) . - This implies that
\(b^2\) is also even, and hence\(b\) must be even. - Since both
\(a\) and\(b\) are even, they have a common factor of 2. This contradicts our initial assumption that\(\frac{a}{b}\) was in its simplest form. - Therefore, the assumption that √2 is rational must be false, which means that √2 is irrational.
Understanding Rational and Irrational Numbers
In mathematics, numbers can be categorized as either rational or irrational. Rational numbers are numbers that can be expressed as the quotient or fraction of two integers, where the numerator is an integer and the denominator is a non-zero integer. Examples of rational numbers include 1/2, 3, and -4.
Rational numbers can be written in the form:
\[\frac{a}{b}\]
where \(a\) and \(b\) are integers and \(b \neq 0\).
On the other hand, irrational numbers cannot be expressed as a simple fraction. They are non-terminating and non-repeating when written as a decimal. The most famous example of an irrational number is the square root of 2. Unlike rational numbers, irrational numbers cannot be written as a ratio of two integers.
Let's look at some properties and examples to understand the differences further:
- Examples of Rational Numbers:
- \(\frac{1}{2}\)
- \(3\) (which can be written as \(\frac{3}{1}\))
- \(-4\) (which can be written as \(\frac{-4}{1}\))
- Examples of Irrational Numbers:
- \(\sqrt{2}\)
- \(\pi\)
- \(e\) (the base of the natural logarithm)
To delve deeper into the concept of irrational numbers, let’s consider the square root of 2. The square root of 2 is known to be irrational because it cannot be expressed as a fraction of two integers. This is a fundamental proof in number theory and helps us understand the nature of irrational numbers more clearly.
The Concept of Square Roots
The concept of square roots is fundamental in mathematics and plays a crucial role in various fields of science and engineering. A square root of a number x is a number y such that y2 = x. For example, the square root of 9 is 3, because 32 = 9. Square roots are closely related to the concept of squaring a number, which involves multiplying the number by itself.
Mathematically, the square root function is denoted as √x. This function has important properties, such as:
- √(x*y) = √x * √y
- √(x/y) = √x / √y
- (√x)2 = x
Square roots can be categorized into two types: rational and irrational square roots. Rational square roots are those that can be expressed as a fraction of two integers, while irrational square roots cannot be expressed in this way.
For instance, the square root of 2 is a classic example of an irrational number. This means that there are no two integers a and b such that (a/b)2 equals 2. This was one of the first proofs that introduced the concept of irrational numbers, significantly impacting the field of mathematics.
Assumption of Rationality
To prove the square root of 2 is irrational, we start by assuming the opposite: that it is rational. This means it can be expressed as a fraction of two integers, say a and b, where a and b have no common factors other than 1, and b is not zero.
Let's express this assumption mathematically:
\[ \sqrt{2} = \frac{a}{b} \]
By squaring both sides, we get:
\[ 2 = \frac{a^2}{b^2} \]
Multiplying both sides by \( b^2 \) to eliminate the fraction, we obtain:
\[ 2b^2 = a^2 \]
This equation tells us that \( a^2 \) is an even number because it is equal to 2 times \( b^2 \). From this, we can infer that \( a \) must also be even (since the square of an odd number is odd).
Since \( a \) is even, we can write it as \( a = 2k \) for some integer \( k \). Substituting this back into the equation, we get:
\[ 2b^2 = (2k)^2 \]
Which simplifies to:
\[ 2b^2 = 4k^2 \]
Or:
\[ b^2 = 2k^2 \]
This tells us that \( b^2 \) is also even, which means \( b \) must be even as well.
However, if both \( a \) and \( b \) are even, they have a common factor of 2. This contradicts our initial assumption that \( a \) and \( b \) have no common factors other than 1.
Therefore, our assumption that \( \sqrt{2} \) is rational must be false. Hence, \( \sqrt{2} \) is irrational.

Proof by Contradiction
To prove that \(\sqrt{2}\) is irrational, we use a method called proof by contradiction. This involves assuming the opposite of what we want to prove and showing that this assumption leads to a contradiction.
Assume that \(\sqrt{2}\) is rational. This means it can be written as a fraction \(\frac{a}{b}\) where \(a\) and \(b\) are integers with no common factors other than 1 (i.e., the fraction is in its simplest form). Therefore, we have:
\[\sqrt{2} = \frac{a}{b}\]
Squaring both sides of the equation gives:
\[2 = \frac{a^2}{b^2}\]
Multiplying both sides by \(b^2\) gives:
\[a^2 = 2b^2\]
This equation shows that \(a^2\) is an even number because it is equal to \(2b^2\). Since \(a^2\) is even, \(a\) must also be even (the square of an odd number is odd). Therefore, we can write \(a\) as:
\[a = 2k\]
for some integer \(k\). Substituting \(2k\) for \(a\) in the equation \(a^2 = 2b^2\), we get:
\[ (2k)^2 = 2b^2 \]
\[ 4k^2 = 2b^2 \]
Dividing both sides by 2, we get:
\[ 2k^2 = b^2 \]
This shows that \(b^2\) is also even, which means \(b\) must be even as well. Therefore, both \(a\) and \(b\) are even, which contradicts our initial assumption that \(a\) and \(b\) have no common factors other than 1.
Since our assumption that \(\sqrt{2}\) is rational leads to a contradiction, we conclude that \(\sqrt{2}\) is irrational.
Squaring the Assumed Rational Expression
To demonstrate that the square root of 2 is irrational, we start by assuming it is rational. This means we can express it as a fraction of two integers, a and b, where a and b are coprime (they have no common factors other than 1).
Assume:
\[\sqrt{2} = \frac{a}{b}\]
Next, we square both sides of the equation to eliminate the square root:
\[2 = \frac{a^2}{b^2}\]
Multiply both sides by \(b^2\) to clear the fraction:
\[2b^2 = a^2\]
This implies that \(a^2\) is an even number since it is equal to 2 times \(b^2\). From this, we can infer that \(a\) itself must be an even number (since the square of an odd number is odd).
Therefore, we can write:
\[a = 2k \text{ for some integer } k\]
Substituting \(2k\) for \(a\) in the equation \(2b^2 = a^2\), we get:
\[2b^2 = (2k)^2\]
Which simplifies to:
\[2b^2 = 4k^2\]
Dividing both sides by 2:
\[b^2 = 2k^2\]
This shows that \(b^2\) is also even, implying that \(b\) must be even as well.
Since both \(a\) and \(b\) are even, they share a common factor of 2, which contradicts our initial assumption that \(a\) and \(b\) are coprime. This contradiction means that our original assumption that \(\sqrt{2}\) is rational must be false.
Therefore, we conclude that \(\sqrt{2}\) is irrational.
Implications for Even and Odd Numbers
To understand the implications for even and odd numbers, we start by squaring the assumed rational expression . This gives us the equation . Since is even (as it is twice ), it follows that itself must be even.
Let for some integer . Substituting this back into the equation, we get:
which simplifies to:
Dividing both sides by 2, we get:
This shows that is also even, implying that is even.
Since both and are even, they have a common factor of 2, contradicting our initial assumption that is in its simplest form. Therefore, this contradiction implies that the assumption that is rational must be false, proving that is irrational.
Analyzing the Even Nature of \( a \)
To analyze the even nature of \( a \) in the proof that the square root of 2 is irrational, we begin by assuming, for the sake of contradiction, that \( \sqrt{2} \) is a rational number. This means we can express \( \sqrt{2} \) as a fraction \( \frac{a}{b} \) where \( a \) and \( b \) are coprime integers (i.e., their greatest common divisor is 1), and \( b \neq 0 \).
Starting from the equation:
\( \sqrt{2} = \frac{a}{b} \)
we can square both sides to obtain:
\( 2 = \frac{a^2}{b^2} \)
Multiplying both sides by \( b^2 \) to clear the fraction gives:
\( 2b^2 = a^2 \)
This implies that \( a^2 \) is even (since it is equal to \( 2b^2 \), which is clearly even because it is 2 times another integer). From this, we deduce that \( a \) must also be even. (Note: The square of an odd number is odd, so \( a \) cannot be odd if \( a^2 \) is even.)
We can express \( a \) as \( 2k \) for some integer \( k \) (since \( a \) is even). Substituting \( 2k \) for \( a \) in the equation \( 2b^2 = a^2 \) gives:
\( 2b^2 = (2k)^2 \)
\( 2b^2 = 4k^2 \)
Dividing both sides by 2 yields:
\( b^2 = 2k^2 \)
This shows that \( b^2 \) is also even (since it is equal to 2 times another integer), which means that \( b \) must be even as well. However, this leads to a contradiction because we initially assumed that \( a \) and \( b \) were coprime (i.e., they have no common factors other than 1). If both \( a \) and \( b \) are even, they share a common factor of 2.
Thus, our assumption that \( \sqrt{2} \) is rational must be false. Therefore, \( \sqrt{2} \) is irrational.

Substitution Back into the Equation
We previously established that if \( p \) and \( q \) are integers such that \( \frac{p}{q} \) is in its simplest form and \( \sqrt{2} = \frac{p}{q} \), then \( p \) must be even. We can express \( p \) as \( p = 2k \) for some integer \( k \).
Let's substitute \( p = 2k \) back into the equation \( 2q^2 = p^2 \):
\[
2q^2 = (2k)^2
\]
Now, simplify the right-hand side:
\[
2q^2 = 4k^2
\]
Next, divide both sides of the equation by 2:
\[
q^2 = 2k^2
\]
This equation shows that \( q^2 \) is also even because it is equal to \( 2 \times k^2 \). Consequently, \( q \) must be even as well. We can express \( q \) as \( q = 2m \) for some integer \( m \).
Substituting \( q = 2m \) back into the equation, we get:
\[
\sqrt{2} = \frac{p}{q} = \frac{2k}{2m} = \frac{k}{m}
\]
Here, \( \frac{k}{m} \) is a fraction simpler than \( \frac{p}{q} \), contradicting our initial assumption that \( \frac{p}{q} \) was in its simplest form. Since both \( p \) and \( q \) are even, they have a common factor of 2, which means they were not in their simplest form.
This contradiction implies that our initial assumption that \( \sqrt{2} \) is rational is incorrect. Thus, \( \sqrt{2} \) cannot be expressed as a ratio of two integers, proving it is irrational.
Implications for \( b \)
Continuing from where we left off in the proof, we have established that \( a \) must be even. We can express \( a \) as \( a = 2k \) for some integer \( k \). Now, we substitute \( a = 2k \) back into the equation \( a^2 = 2b^2 \) to further analyze the implications for \( b \).
Starting with the equation:
Substitute \( a = 2k \) into the equation:
Divide both sides of the equation by 2:
This equation shows that \( b^2 \) is also even, as it is equal to 2 times \( k^2 \), which is an integer. From this, we can conclude that \( b \) must also be even. Therefore, we can express \( b \) as \( b = 2m \) for some integer \( m \).
At this point, we have shown that both \( a \) and \( b \) are even, meaning they both have a common factor of 2. This contradicts our initial assumption that \( \frac{a}{b} \) is in its simplest form, with \( a \) and \( b \) having no common factors other than 1. This contradiction implies that our original assumption that \( \sqrt{2} \) is rational is false. Hence, \( \sqrt{2} \) must be irrational.
To summarize:
- We started with the assumption that \( \sqrt{2} \) is rational, so it can be expressed as \( \frac{a}{b} \) in simplest form.
- We showed that \( a \) must be even, so \( a = 2k \) for some integer \( k \).
- Substituting \( a = 2k \) back into the equation \( a^2 = 2b^2 \), we derived \( 2k^2 = b^2 \), showing that \( b \) must also be even, so \( b = 2m \) for some integer \( m \).
- This means both \( a \) and \( b \) have a common factor of 2, contradicting our assumption that they are coprime.
- Therefore, \( \sqrt{2} \) cannot be rational and must be irrational.
Identifying the Contradiction
In this section, we will identify the contradiction that arises from the assumption that \( \sqrt{2} \) is rational. Recall that we assumed \( \sqrt{2} \) can be expressed as the fraction \( \frac{a}{b} \) in its lowest terms, where \( a \) and \( b \) are coprime integers. We derived the equation:
\[ 2b^2 = a^2 \]
We concluded that \( a \) must be even, so let \( a = 2k \) for some integer \( k \). Substituting \( a = 2k \) back into the equation gives:
\[ 2b^2 = (2k)^2 \]
\[ 2b^2 = 4k^2 \]
\[ b^2 = 2k^2 \]
This result implies that \( b^2 \) is also even. If \( b^2 \) is even, then \( b \) must be even. Let \( b = 2m \) for some integer \( m \). Now, substituting \( b = 2m \) back into the equation \( b^2 = 2k^2 \) gives:
\[ (2m)^2 = 2k^2 \]
\[ 4m^2 = 2k^2 \]
\[ 2m^2 = k^2 \]
Therefore, \( k^2 \) is also even, which means \( k \) must be even. However, if both \( a \) and \( b \) are even, this contradicts our original assumption that \( \frac{a}{b} \) is in its lowest terms, because both \( a \) and \( b \) would have a common factor of 2. Thus, our assumption that \( \sqrt{2} \) is rational leads to a contradiction.
Therefore, we conclude that \( \sqrt{2} \) cannot be expressed as a ratio of two integers, and hence it is irrational.
Conclusion of the Proof
In conclusion, we started with the assumption that the square root of 2, denoted as \( \sqrt{2} \), is a rational number. This means it can be expressed as a fraction in the form \( \frac{a}{b} \), where \( a \) and \( b \) are coprime integers (having no common factors other than 1) and \( b \neq 0 \).
By squaring both sides of the equation \( \sqrt{2} = \frac{a}{b} \), we obtained:
\( 2 = \frac{a^2}{b^2} \)
Multiplying both sides by \( b^2 \) to clear the fraction, we arrived at:
\( 2b^2 = a^2 \)
This equation shows that \( a^2 \) is even (since it is equal to 2 times \( b^2 \), and any multiple of 2 is even). Consequently, \( a \) must also be even because the square of an odd number is odd. Therefore, we can express \( a \) as \( a = 2k \) for some integer \( k \).
Substituting \( a = 2k \) back into the equation, we get:
\( 2b^2 = (2k)^2 \)
\( 2b^2 = 4k^2 \)
Dividing both sides by 2, we find:
\( b^2 = 2k^2 \)
Now, this implies that \( b^2 \) is also even, and therefore \( b \) must be even as well. Let \( b = 2m \) for some integer \( m \).
At this stage, we have shown that both \( a \) and \( b \) are even, meaning they have a common factor of 2. This contradicts our original assumption that \( a \) and \( b \) are coprime. Since our initial assumption led to a contradiction, we must conclude that \( \sqrt{2} \) cannot be expressed as a ratio of two integers, i.e., \( \sqrt{2} \) is irrational.
Thus, we have proven by contradiction that the square root of 2 is irrational.

Significance and Applications of the Proof
The proof that the square root of 2 is irrational holds significant importance in both mathematical theory and its applications. Here are some key points highlighting its impact:
- Foundation of Number Theory: The proof demonstrates a fundamental distinction between rational and irrational numbers. It provides an example of how not all numbers can be expressed as a fraction of two integers, which is essential in understanding the structure and properties of real numbers.
- Historical Impact: This discovery, attributed to the ancient Greeks, particularly the Pythagoreans, marked a crucial point in the history of mathematics. It challenged the existing belief that all numbers were rational and led to the development of more sophisticated mathematical concepts and theories.
- Geometric Applications: The irrationality of \(\sqrt{2}\) has practical implications in geometry. For instance, it explains why the diagonal of a square cannot be perfectly measured using the sides of the square, influencing architectural designs and constructions throughout history, including methods used by the Romans.
- Mathematical Proof Techniques: The proof employs a method called proof by contradiction, which has become a staple technique in mathematics. This method is used to prove various other important theorems and is a fundamental part of mathematical logic and reasoning.
- Computational Mathematics: Understanding the properties of irrational numbers like \(\sqrt{2}\) is crucial in numerical methods and computational algorithms. Approximations of \(\sqrt{2}\) are used in various algorithms for calculating square roots and in other numerical analyses.
- Real-World Engineering and Science: The concepts derived from the proof are applied in fields such as physics, engineering, and computer science. For example, the precision required in measurements and calculations in these fields often relies on understanding and working with irrational numbers.
The irrationality of \(\sqrt{2}\) is more than just a mathematical curiosity; it is a pivotal concept that has influenced various domains of knowledge and continues to be relevant in both theoretical and applied mathematics.
Historical Context and Development
The discovery of the irrationality of the square root of 2 has significant historical roots, often attributed to ancient Greek mathematicians. The most commonly associated figure with this discovery is Hippasus of Metapontum, a student of Pythagoras.
According to legend, Hippasus made this discovery while exploring the properties of the diagonal of a square with unit side lengths, which leads to the conclusion that the diagonal’s length is \( \sqrt{2} \). This discovery was controversial because it contradicted the Pythagorean belief that all numbers could be expressed as the ratio of two integers, i.e., as rational numbers.
The ancient Greeks' understanding of numbers was deeply connected to their philosophy and worldview. Pythagoreans believed in the perfection of numbers and that all phenomena in the universe could be explained in terms of whole numbers and their ratios. The discovery of irrational numbers, therefore, posed a philosophical crisis, leading to myths that Hippasus was punished, possibly even drowned, for revealing such a disruptive truth.
Despite the initial resistance, the proof of the irrationality of \( \sqrt{2} \) marked a pivotal moment in the development of mathematics. It not only expanded the understanding of number systems but also laid the groundwork for future developments in algebra and calculus.
Over centuries, the rigorous formalization of the concept of irrational numbers continued, notably during the period of ancient Greek mathematics and later in the works of mathematicians during the Renaissance and the Enlightenment. The acceptance and further exploration of irrational numbers have had profound implications in various fields, including geometry, algebra, and number theory, influencing mathematical thought profoundly.
Today, the proof that \( \sqrt{2} \) is irrational is a fundamental topic in introductory mathematics courses, illustrating the beauty and depth of mathematical reasoning. It serves as a classic example of proof by contradiction and continues to be a significant educational tool for developing logical thinking and problem-solving skills.
Common Misconceptions
There are several common misconceptions regarding the proof that the square root of 2 is irrational. Understanding these can help clarify the nature of the proof and the concept of irrational numbers.
-
Misconception 1: Rational numbers can always be written in fractional form.
While it's true that rational numbers can be expressed as fractions \( \frac{a}{b} \), where \(a\) and \(b\) are integers, the proof for \( \sqrt{2} \)'s irrationality shows that \( \sqrt{2} \) cannot be expressed in such a form where \(a\) and \(b\) are co-prime (i.e., having no common factors other than 1).
-
Misconception 2: The proof by contradiction is not rigorous.
The proof by contradiction is a fundamental and rigorous method in mathematics. By assuming that \( \sqrt{2} \) is rational and then demonstrating that this assumption leads to a logical contradiction, the proof confirms that \( \sqrt{2} \) must be irrational.
-
Misconception 3: Only advanced mathematics can prove irrationality.
In fact, the proof that \( \sqrt{2} \) is irrational uses basic principles of arithmetic and number theory. It does not require advanced mathematics but relies on understanding the properties of even and odd numbers and basic algebra.
-
Misconception 4: Irrational numbers are rare or exceptional cases.
Irrational numbers are actually quite common. Numbers such as \( \pi \) and \( e \) are also irrational. The discovery of irrational numbers expanded the understanding of the number system, showing that it is more extensive than just the rationals.
By addressing these misconceptions, we can better appreciate the elegance and significance of the proof that the square root of 2 is irrational. It highlights the richness of mathematical concepts and the importance of rigorous proof methods in establishing mathematical truths.
Further Reading and References
To gain a deeper understanding of the proof that the square root of 2 is irrational and explore related mathematical concepts, consider the following resources:
-
Euclid's Proof:
Euclid's original proof is a classic example of a proof by contradiction. This method shows that if we assume \(\sqrt{2}\) is rational, we end up with a logical contradiction. Detailed explanations of Euclid's proof can be found in numerous mathematical texts and online resources.
-
ProofWiki:
ProofWiki provides a comprehensive look at various proofs of the irrationality of \(\sqrt{2}\). It includes different methods and perspectives, making it a valuable resource for students and enthusiasts. Visit ProofWiki to explore these proofs in detail.
-
Math is Fun:
The "Math is Fun" website offers a user-friendly explanation of the proof. It breaks down the steps and provides a clear understanding of the concepts involved, making it accessible to learners at different levels.
-
Books and Publications:
Several books cover the topic extensively. Notable mentions include:
- A Course of Analysis by E.G. Phillips
- Modern Algebra by Seth Warner
- Calculus and Linear Algebra by Wilfred Kaplan and Donald J. Lewis
These texts offer in-depth discussions on the proof and its implications.
-
Academic Journals:Research articles and papers published in mathematical journals provide detailed analyses and advanced discussions on the topic. Accessing these through academic databases can offer deeper insights and ongoing research in the field.
Exploring these resources will enhance your understanding of the proof of the irrationality of \(\sqrt{2}\) and its broader mathematical context.
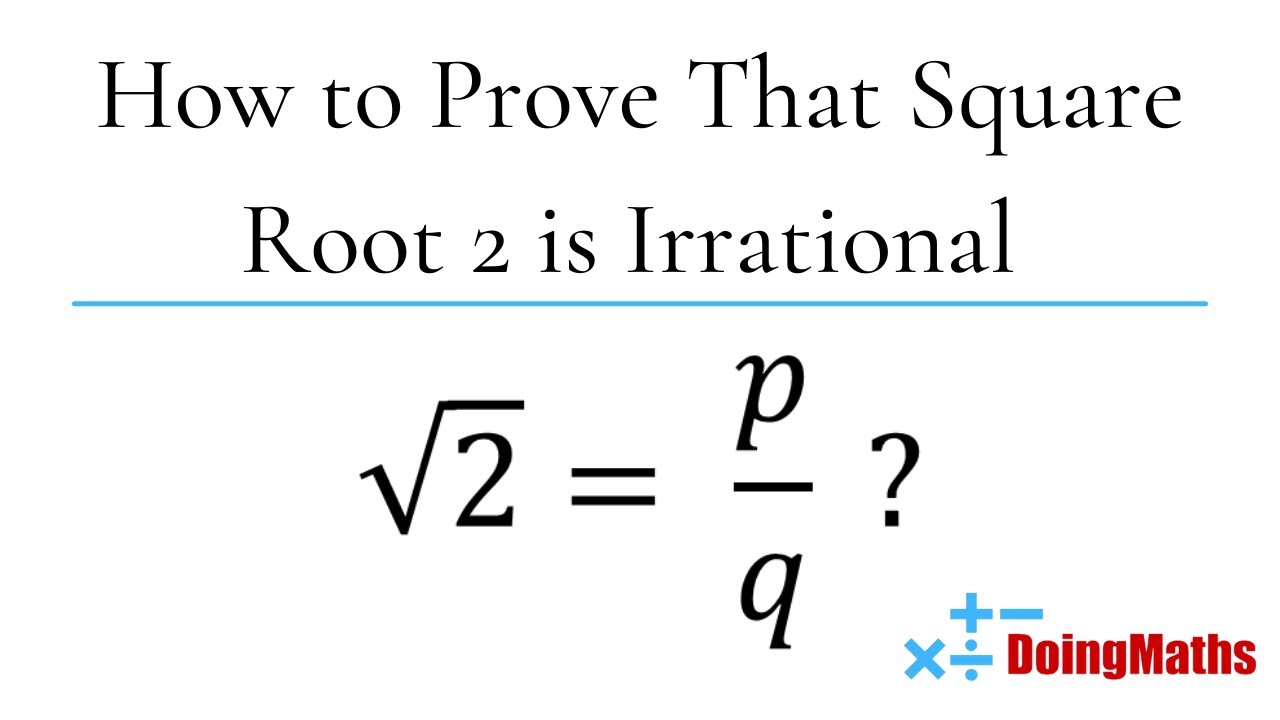
Video này chứng minh rằng căn bậc hai của 2 là số vô tỉ, sử dụng phương pháp chứng minh phản chứng. Hãy khám phá sự thú vị của toán học!
Chứng Minh: Căn Bậc Hai của 2 là Số Vô Tỉ
READ MORE:
Bằng chứng rằng căn bậc hai của 2 là vô tỉ | Đại số I | Khan Academy