Derivative of Square Root of 2-x: A Comprehensive Guide

The derivative of a function involving a square root can be found using the chain rule. Let's find the derivative of the function:

$$


2
−
x

Steps to Find the Derivative

1. Rewrite the square root function in exponent form:

   $$
   
   2
   −
   x
   
   
   
   
   1
   2
   
   
   

2. Apply the chain rule, which states:

   $$
   
   
   1
   
   
   2
   
   
   2
   −
   x
   
   
   
   
   ∗
   (
   
   
   −
   1
   
   
   
   
   
   1
   2
   
   
   
   
   )
   

3. Simplify the expression:

   $$
   
   
   −
   1
   
   
   2
   
   
   2
   −
   x
   
   
   
   
   

Final Derivative

Thus, the derivative of the function $$


2
−
x


is:

$$

−

1

2


2
−
x

Derivatives are fundamental concepts in calculus that measure how a function changes as its input changes. They provide insights into the behavior of functions and are widely used in various fields such as physics, engineering, and economics. In essence, a derivative represents the rate of change or the slope of a function at a given point.

• Definition: The derivative of a function at a point is defined as the limit of the average rate of change of the function over an interval as the interval approaches zero.
• Notation: Derivatives are commonly denoted by symbols such as f'(x), dy/dx, or Df(x).
• Basic Rules: Several rules are essential for calculating derivatives, including the power rule, product rule, quotient rule, and chain rule.
• Power Rule: The power rule is used to find the derivative of functions of the form x^n, where the derivative is given by nx^(n-1).
• Chain Rule: The chain rule is used to differentiate composite functions. If a function y = f(g(x)), then its derivative is given by dy/dx = f'(g(x)) * g'(x).
• Applications: Derivatives have numerous applications, including finding the maxima and minima of functions, solving motion problems, and optimizing processes in various industries.

Understanding derivatives is crucial for analyzing and interpreting the behavior of functions. They provide the tools needed to model real-world phenomena and solve complex problems in mathematics and science.

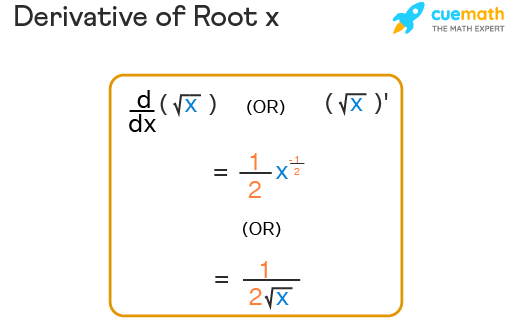
The square root function is a fundamental concept in mathematics, particularly in calculus. It is represented as \( \sqrt{x} \) and can be expressed using a rational exponent as \( x^{1/2} \). Understanding how to differentiate this function is essential for solving many calculus problems.

To differentiate the square root function, we use the power rule. The power rule states that if you have a function \( f(x) = x^n \), its derivative is given by \( f'(x) = nx^{n-1} \). When dealing with the square root function \( f(x) = \sqrt{x} = x^{1/2} \), we apply this rule:

• First, rewrite the square root as a power: \( \sqrt{x} = x^{1/2} \).
• Next, apply the power rule: \( \frac{d}{dx}(x^{1/2}) = \frac{1}{2}x^{-1/2} \).
• Finally, rewrite the result in a more conventional form: \( \frac{1}{2}x^{-1/2} = \frac{1}{2\sqrt{x}} \).

This process can be extended to more complex functions involving square roots, such as \( \sqrt{2-x} \). To differentiate such a function, we use the chain rule in addition to the power rule.

For example, to find the derivative of \( f(x) = \sqrt{2-x} \), follow these steps:

1. Rewrite the function: \( f(x) = (2-x)^{1/2} \).
2. Let \( u = 2-x \), so \( f(x) = u^{1/2} \).
3. Differentiate the outer function with respect to \( u \): \( \frac{d}{du}(u^{1/2}) = \frac{1}{2}u^{-1/2} = \frac{1}{2\sqrt{u}} \).
4. Differentiate \( u \) with respect to \( x \): \( \frac{d}{dx}(2-x) = -1 \).
5. Apply the chain rule: \( \frac{d}{dx}(\sqrt{2-x}) = \frac{1}{2\sqrt{2-x}} \cdot (-1) = -\frac{1}{2\sqrt{2-x}} \).

This step-by-step approach ensures a clear understanding of the differentiation process for functions involving square roots, crucial for tackling more advanced calculus problems.

The Chain Rule is a fundamental concept in calculus used to differentiate composite functions. It allows us to find the derivative of a function that is composed of two or more functions. The Chain Rule is typically expressed as:

\[ \frac{d}{dx} [f(g(x))] = f'(g(x)) \cdot g'(x) \]

Here’s a step-by-step explanation of how to use the Chain Rule:

1. Identify the outer and inner functions: Consider a composite function like \( f(g(x)) \). The outer function is \( f(u) \) and the inner function is \( u = g(x) \).
2. Differentiate the outer function: Find the derivative of the outer function with respect to the inner function, \( f'(u) \).
3. Differentiate the inner function: Find the derivative of the inner function with respect to \( x \), \( g'(x) \).
4. Apply the Chain Rule: Multiply the derivative of the outer function by the derivative of the inner function to get the derivative of the composite function.

Let’s apply the Chain Rule to a specific example:

• Example: Differentiate \( \sqrt{2-x} \).
• Step 1: Rewrite the function as \( (2-x)^{1/2} \).
• Step 2: Identify the outer function \( f(u) = u^{1/2} \) and the inner function \( u = 2 - x \).
• Step 3: Differentiate the outer function: \( f'(u) = \frac{1}{2} u^{-1/2} \).
• Step 4: Differentiate the inner function: \( g'(x) = -1 \).
• Step 5: Apply the Chain Rule: \( \frac{d}{dx} \sqrt{2-x} = \frac{1}{2} (2-x)^{-1/2} \cdot (-1) \).
• Step 6: Simplify the result: \( \frac{d}{dx} \sqrt{2-x} = -\frac{1}{2\sqrt{2-x}} \).

Using the Chain Rule simplifies the process of finding the derivative of composite functions, making it an essential tool in calculus.

The chain rule is an essential tool in calculus for finding the derivative of composite functions. In this section, we will apply the chain rule to the function \( \sqrt{2-x} \).

1. Step 1: Identify the Outer and Inner Functions

   Consider the function \( f(x) = \sqrt{2-x} \). Here, the outer function is \( \sqrt{u} \) where \( u = 2-x \).

2. Step 2: Differentiate the Outer Function

   First, differentiate the outer function with respect to \( u \):

   \( \frac{d}{du} \sqrt{u} = \frac{1}{2\sqrt{u}} \)

3. Step 3: Differentiate the Inner Function

   Next, differentiate the inner function \( u = 2-x \) with respect to \( x \):

   \( \frac{d}{dx} (2-x) = -1 \)

4. Step 4: Apply the Chain Rule

   Now, apply the chain rule which states that the derivative of the composite function \( f(g(x)) \) is \( f'(g(x)) \cdot g'(x) \):

   \( \frac{d}{dx} \sqrt{2-x} = \frac{d}{du} \sqrt{u} \cdot \frac{d}{dx} (2-x) \)

   Substituting the derivatives we found, we get:

   \( \frac{d}{dx} \sqrt{2-x} = \frac{1}{2\sqrt{2-x}} \cdot (-1) \)

   Therefore, the derivative of \( \sqrt{2-x} \) is:

   \( \frac{d}{dx} \sqrt{2-x} = -\frac{1}{2\sqrt{2-x}} \)

By following these steps, you can successfully apply the chain rule to differentiate functions involving square roots and other composite functions.

The process of finding the derivative of the square root of \(2-x\) involves applying the chain rule in differentiation. Here is a detailed step-by-step calculation:

1. Identify the function and its inner function:

   • Outer function: \( f(u) = \sqrt{u} \)
   • Inner function: \( u(x) = 2 - x \)

2. Find the derivative of the outer function \( f(u) \):

   \[
   \frac{d}{du} \left( \sqrt{u} \right) = \frac{1}{2\sqrt{u}}
   \]

3. Find the derivative of the inner function \( u(x) \):

   \[
   \frac{d}{dx} (2 - x) = -1
   \]

4. Apply the chain rule:

   \[
   \frac{d}{dx} \left( \sqrt{2 - x} \right) = \frac{d}{du} \left( \sqrt{u} \right) \cdot \frac{d}{dx} \left( 2 - x \right)
   \]

5. Substitute \( u = 2 - x \) back into the derivative of the outer function and multiply by the derivative of the inner function:

   \[
   \frac{d}{dx} \left( \sqrt{2 - x} \right) = \frac{1}{2\sqrt{2 - x}} \cdot (-1) = -\frac{1}{2\sqrt{2 - x}}
   \]

Thus, the derivative of the square root of \(2-x\) is:

\[
\frac{d}{dx} \left( \sqrt{2 - x} \right) = -\frac{1}{2\sqrt{2 - x}}

After applying the chain rule to differentiate the square root of \(2-x\), we obtain the intermediate form of the derivative. The next step is to simplify this result for clarity and ease of use.

1. Start with the derivative obtained using the chain rule:

   \[
   \frac{d}{dx} (\sqrt{2-x}) = \frac{1}{2\sqrt{2-x}} \cdot (-1)
   \]

2. Combine the constants and simplify the expression:

   \[
   \frac{d}{dx} (\sqrt{2-x}) = -\frac{1}{2\sqrt{2-x}}
   \]

3. Rewrite the simplified result for final clarity:

   \[
   -\frac{1}{2\sqrt{2-x}}
   \]

This final simplified form of the derivative is more straightforward to work with in subsequent calculations and applications.

When calculating the derivative of the square root of \(2-x\), there are several common mistakes that students often make. Understanding these can help you avoid them and ensure accurate results.

• **Incorrect Application of the Chain Rule**: Remember to correctly apply the chain rule. If \( f(x) = \sqrt{2 - x} \), rewrite it as \( f(x) = (2 - x)^{1/2} \). The derivative requires applying the power rule and then multiplying by the derivative of the inner function \( 2 - x \).
• **Forgetting to Multiply by the Derivative of the Inner Function**: After using the power rule, don’t forget to multiply by the derivative of \( 2 - x \), which is \(-1\). The correct derivative is \( \frac{1}{2}(2 - x)^{-1/2} \times (-1) \).
• **Rationalizing the Denominator Incorrectly**: When simplifying, make sure to rationalize correctly if needed. Incorrect steps in rationalization can lead to wrong answers.
• **Simplifying Errors**: Double-check your algebraic simplifications. Common errors include incorrectly simplifying the fraction or mishandling negative exponents.

By being aware of these common pitfalls, you can avoid mistakes and accurately determine the derivative of \(\sqrt{2 - x}\).

The derivative of the function involving the square root of \(2-x\) has various practical applications in fields such as physics, engineering, and economics. Below, we explore several examples to illustrate how this derivative can be utilized.

Example 1: Finding the Slope of a Tangent Line

Consider the function \( f(x) = \sqrt{2-x} \). To find the slope of the tangent line to the curve at \( x = 1 \), we first need to find the derivative \( f'(x) \).

The derivative is:

\[
f'(x) = \frac{d}{dx} \left( \sqrt{2-x} \right) = \frac{-1}{2\sqrt{2-x}}
\]

Now, substitute \( x = 1 \) into the derivative:

\[
f'(1) = \frac{-1}{2\sqrt{2-1}} = \frac{-1}{2\sqrt{1}} = \frac{-1}{2}
\]

Therefore, the slope of the tangent line at \( x = 1 \) is \( -\frac{1}{2} \).

Example 2: Rate of Change in Physics

In physics, the function \( s(t) = \sqrt{2-t} \) could represent the displacement \( s \) of an object over time \( t \). To find the velocity \( v(t) \) of the object at a specific time, we take the derivative of \( s(t) \).

The velocity function is:

\[
v(t) = s'(t) = \frac{d}{dx} \left( \sqrt{2-t} \right) = \frac{-1}{2\sqrt{2-t}}
\]

For instance, to find the velocity at \( t = 0.5 \):

\[
v(0.5) = \frac{-1}{2\sqrt{2-0.5}} = \frac{-1}{2\sqrt{1.5}} = \frac{-1}{2 \cdot \sqrt{1.5}}
\]

This provides the rate at which the displacement is changing at \( t = 0.5 \).

Example 3: Optimization in Economics

In economics, the function \( C(x) = \sqrt{2-x} \) might represent the cost \( C \) of producing \( x \) units of a good. To maximize profit or minimize cost, we need to understand the rate of change of the cost function, which is given by its derivative.

The marginal cost function is:

\[
C'(x) = \frac{d}{dx} \left( \sqrt{2-x} \right) = \frac{-1}{2\sqrt{2-x}}
\]

If a company wants to determine the marginal cost when producing 0.8 units, they would calculate:

\[
C'(0.8) = \frac{-1}{2\sqrt{2-0.8}} = \frac{-1}{2\sqrt{1.2}} = \frac{-1}{2 \cdot \sqrt{1.2}}
\]

This calculation helps in making informed decisions about production levels.

Conclusion

Understanding the derivative of \( \sqrt{2-x} \) is crucial for analyzing and solving problems in various domains. Whether determining the slope of a tangent line, calculating the rate of change in physical scenarios, or optimizing costs in economics, this derivative provides valuable insights and solutions.

• Q: What is the derivative of \( \sqrt{2 - x} \)?

  A: The derivative of \( \sqrt{2 - x} \) can be found using the chain rule. It is given by:

  \[
  \frac{d}{dx}\left(\sqrt{2 - x}\right) = \frac{d}{dx}\left((2 - x)^{\frac{1}{2}}\right) = \frac{1}{2}(2 - x)^{-\frac{1}{2}} \cdot (-1) = -\frac{1}{2\sqrt{2 - x}}
  \]

• Q: How do you apply the chain rule to find the derivative of a square root function?

  A: To apply the chain rule, identify the outer function and the inner function. For \( \sqrt{2 - x} \), the outer function is \( \sqrt{u} \) and the inner function is \( 2 - x \). Differentiate the outer function with respect to the inner function, and then multiply by the derivative of the inner function:

  \[
  \frac{d}{dx}\left(\sqrt{2 - x}\right) = \frac{d}{du}\left(\sqrt{u}\right) \cdot \frac{d}{dx}(2 - x) = \frac{1}{2\sqrt{u}} \cdot (-1) = -\frac{1}{2\sqrt{2 - x}}
  \]

• Q: What are some common mistakes to avoid when differentiating square root functions?

  A: Common mistakes include:
  

  
  
  1. Forgetting to apply the chain rule when the argument of the square root is more complex than just \( x \).
  
  
  2. Incorrectly simplifying the derivative after applying the chain rule.
  
  
  3. Ignoring the negative sign when differentiating expressions like \( 2 - x \).
  
  
  
  



• Q: Can you provide a step-by-step example for differentiating \( \sqrt{3x^2 - x} \)?

  A: Sure! Let's differentiate \( \sqrt{3x^2 - x} \) using the chain rule:
  

  
  
  1. Let \( u = 3x^2 - x \). Then, the function becomes \( \sqrt{u} \).
  
  
  2. The outer function is \( \sqrt{u} \), and its derivative is \( \frac{1}{2\sqrt{u}} \).
  
  
  3. The inner function is \( 3x^2 - x \), and its derivative is \( 6x - 1 \).
  
  
  4. Applying the chain rule, we get:
     \[
     \frac{d}{dx}\left(\sqrt{3x^2 - x}\right) = \frac{1}{2\sqrt{3x^2 - x}} \cdot (6x - 1) = \frac{6x - 1}{2\sqrt{3x^2 - x}}
     \]
     
  
  
  
  



• Q: How is the derivative of \( \sqrt{x} \) different from more complex square root functions?

  A: The derivative of \( \sqrt{x} \) is simpler because the inner function is just \( x \). Its derivative is:
  \[
  \frac{d}{dx}\left(\sqrt{x}\right) = \frac{1}{2\sqrt{x}}
  \]
  For more complex square root functions, such as \( \sqrt{2 - x} \) or \( \sqrt{3x^2 - x} \), you need to use the chain rule to account for the inner function's derivative.

For a deeper understanding of derivatives, especially those involving square root functions, the following resources provide comprehensive explanations, examples, and tools:

• Khan Academy: Derivative of Square Root Functions

  This resource offers detailed video tutorials on how to differentiate functions involving square roots using the chain rule. It's perfect for visual learners who benefit from step-by-step explanations.

• Mathway: Derivative Calculator

  Mathway provides an online tool to calculate derivatives of various functions, including those with square roots. It supports multiple differentiation methods and offers detailed solutions.

• Cuemath: Derivatives of Root Functions

  Cuemath explains the process of differentiating root functions, including multiple examples and common mistakes to avoid. It is a great resource for understanding the theoretical aspects and practical applications of derivatives.

• MathPortal: Comprehensive Calculus Tools

  MathPortal offers a variety of calculus tools, including a derivative calculator, to help solve and understand derivatives step-by-step. It is useful for both students and teachers looking for reliable computational resources.

• Derivative Calculator

  This online calculator provides solutions for derivatives and allows users to input custom functions. It explains the steps involved in finding the derivative, which is beneficial for learning and verification purposes.

These resources will not only help you understand the derivative of square root functions but also improve your overall calculus skills.