Square Root of 2-x: Understanding and Applying the Function

The mathematical expression \( \sqrt{2 - x} \) involves the square root function applied to the linear expression \( 2 - x \). This function has several interesting properties and considerations, especially in terms of its domain, range, and graphical representation.

Domain of \( \sqrt{2 - x} \)

For the square root function to be defined, the expression inside the square root must be non-negative. Therefore, we need:

\( 2 - x \geq 0 \)

Solving this inequality gives:

\( x \leq 2 \)

Thus, the domain of \( \sqrt{2 - x} \) is all real numbers \( x \) such that \( x \leq 2 \). In interval notation, this is expressed as:

\( (-\infty, 2] \)

Range of \( \sqrt{2 - x} \)

The square root function outputs non-negative values for non-negative inputs. Therefore, as long as \( 2 - x \) is non-negative, the output of \( \sqrt{2 - x} \) will also be non-negative. This means the range of the function is:

\( [0, \infty) \)

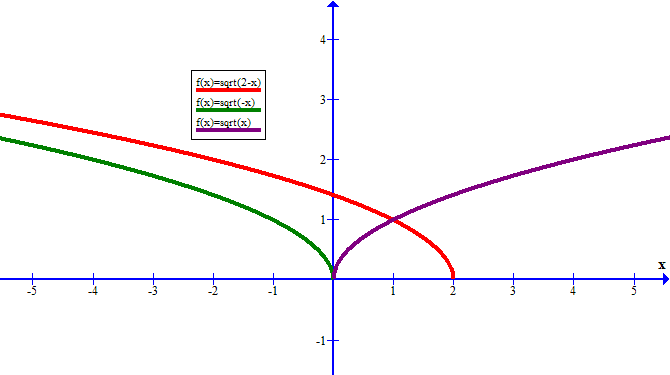
Graphical Representation

The graph of \( \sqrt{2 - x} \) can be plotted by considering the points where \( 2 - x \) equals certain values:

• When \( x = 2 \), \( \sqrt{2 - x} = \sqrt{0} = 0 \).
• When \( x = 1 \), \( \sqrt{2 - x} = \sqrt{1} = 1 \).
• When \( x = 0 \), \( \sqrt{2 - x} = \sqrt{2} \approx 1.414 \).
• As \( x \) decreases towards \(-\infty\), \( \sqrt{2 - x} \) increases without bound.

The graph starts at the point (2, 0) and extends to the left, gradually increasing as \( x \) decreases.

Applications and Examples

The expression \( \sqrt{2 - x} \) appears in various mathematical contexts, such as in solving equations and inequalities, and in certain optimization problems. Here are a few examples:

1. Solving Equations: Finding \( x \) such that \( \sqrt{2 - x} = k \), where \( k \) is a constant.
2. Integration: Integrating \( \sqrt{2 - x} \) with respect to \( x \) involves using a suitable substitution to simplify the integral.
3. Optimization: In problems where minimizing or maximizing the function \( \sqrt{2 - x} \) is required, understanding its domain and range is crucial.

The expression \( \sqrt{2 - x} \) is a mathematical function that combines the square root operation with a linear transformation. Understanding this function involves exploring its definition, properties, and various applications. Below, we delve into the key aspects of \( \sqrt{2 - x} \).

Definition:

The square root of \( 2 - x \) is defined as:

\[
\sqrt{2 - x}
\]

where \( x \) is a real number. For the function to be real-valued, the expression inside the square root must be non-negative.

Properties:

• Domain: The domain of \( \sqrt{2 - x} \) consists of all real numbers \( x \) such that \( 2 - x \geq 0 \). This simplifies to \( x \leq 2 \).
• Range: Since the square root function produces non-negative results, the range of \( \sqrt{2 - x} \) is \([0, \infty)\).
• Continuity: The function \( \sqrt{2 - x} \) is continuous for all \( x \) in its domain.

Graphical Representation:

The graph of \( \sqrt{2 - x} \) starts at the point (2, 0) and extends to the left, increasing gradually as \( x \) decreases. The function is defined only for \( x \leq 2 \).

Steps to Understand the Function:

1. Identify the domain by solving the inequality \( 2 - x \geq 0 \).
2. Determine the range by considering the output of the square root function.
3. Plot key points on the graph, such as \( (2, 0) \), \( (1, 1) \), and \( (0, \sqrt{2}) \).
4. Analyze the behavior of the function as \( x \) approaches its boundaries.

By mastering these steps, you can gain a comprehensive understanding of the square root of \( 2 - x \), its properties, and how to apply it in various mathematical contexts.

The function \( \sqrt{2 - x} \) is an important mathematical expression involving the square root of a linear term. To fully understand this function, we need to explore its definition and key properties.

Mathematical Definition:

The expression \( \sqrt{2 - x} \) is defined as the principal (non-negative) square root of \( 2 - x \), where \( x \) is a real number. Formally, it is expressed as:

\[
\sqrt{2 - x}
\]

For the square root to be defined, the radicand (the expression inside the square root) must be non-negative. Therefore, we have the condition:

\[
2 - x \geq 0
\]

This inequality simplifies to:

\[
x \leq 2
\]

Properties of \( \sqrt{2 - x} \):

• Domain: The domain of the function \( \sqrt{2 - x} \) consists of all real numbers \( x \) such that \( x \leq 2 \). In interval notation, this is written as \( (-\infty, 2] \).
• Range: Since the square root function only produces non-negative results, the range of \( \sqrt{2 - x} \) is \([0, \infty)\).
• Continuity: The function is continuous for all \( x \) in its domain. There are no breaks, jumps, or holes in the graph of the function within this interval.
• Increasing/Decreasing Behavior: The function \( \sqrt{2 - x} \) is a decreasing function. As \( x \) increases, the value of \( \sqrt{2 - x} \) decreases.
• Endpoints: At \( x = 2 \), the function evaluates to \( \sqrt{0} = 0 \). As \( x \) approaches \(-\infty\), the value of \( \sqrt{2 - x} \) increases without bound.

Graphical Representation:

The graph of \( \sqrt{2 - x} \) is a curve that starts at the point (2, 0) and extends to the left, gradually increasing as \( x \) decreases. Key points on the graph include:

• \((2, 0)\)
• \((1, 1)\)
• \((0, \sqrt{2})\)

Steps to Analyze the Function:

1. Determine the domain by solving the inequality \( 2 - x \geq 0 \).
2. Identify the range by considering the non-negative outputs of the square root function.
3. Plot key points to understand the shape and direction of the graph.
4. Observe the function's behavior as \( x \) approaches the boundaries of its domain.

By following these steps and understanding the mathematical definition and properties of \( \sqrt{2 - x} \), you can effectively work with this function in various mathematical problems and applications.

The function \( \sqrt{2 - x} \) is defined by taking the square root of the expression \( 2 - x \). To fully understand this function, it is important to analyze its domain and range.

Domain of the Function:

The domain of a function is the set of all possible input values (x-values) for which the function is defined. For the function \( \sqrt{2 - x} \), the expression inside the square root must be non-negative. This leads to the inequality:

\[
2 - x \geq 0
\]

Solving for \( x \), we get:

\[
x \leq 2
\]

Thus, the domain of \( \sqrt{2 - x} \) is all real numbers less than or equal to 2. In interval notation, this is expressed as:

\[
(-\infty, 2]
\]

Range of the Function:

The range of a function is the set of all possible output values (y-values) that the function can produce. For \( \sqrt{2 - x} \), the square root function always produces non-negative values. Therefore, the output of \( \sqrt{2 - x} \) is also non-negative. We consider the following points:

• When \( x = 2 \), \( \sqrt{2 - x} = \sqrt{0} = 0 \).
• As \( x \) decreases from 2, the value of \( \sqrt{2 - x} \) increases.
• There is no upper limit to the values of \( \sqrt{2 - x} \) as \( x \) approaches \(-\infty\).

Therefore, the range of \( \sqrt{2 - x} \) is all non-negative real numbers. In interval notation, this is expressed as:

\[
[0, \infty)
\]

Summary:

Understanding the domain and range of the function \( \sqrt{2 - x} \) is crucial for accurately graphing the function and solving related mathematical problems. By ensuring that \( x \) values fall within the specified domain, we guarantee that the function produces valid and meaningful outputs.

Solving equations that involve the function \( \sqrt{2 - x} \) requires understanding the properties of square roots and applying algebraic techniques. Below, we outline the steps to solve such equations, illustrated with examples.

General Steps to Solve Equations Involving \( \sqrt{2 - x} \):

1. Isolate the Square Root: Move all terms involving \( \sqrt{2 - x} \) to one side of the equation and other terms to the opposite side.
2. Square Both Sides: To eliminate the square root, square both sides of the equation.
3. Simplify and Solve for \( x \): Simplify the resulting equation and solve for \( x \).
4. Check for Extraneous Solutions: Substitute the solutions back into the original equation to ensure they are valid within the domain of the function.

Example 1: Solve \( \sqrt{2 - x} = 1 \)

1. Isolate the Square Root: The square root is already isolated.
2. Square Both Sides:

   \[
   (\sqrt{2 - x})^2 = 1^2
   \]

   \[
   2 - x = 1
   \]

3. Simplify and Solve for \( x \):

   \[
   2 - x = 1
   \]

   \[
   -x = 1 - 2
   \]

   \[
   -x = -1
   \]

   \[
   x = 1
   \]

4. Check for Extraneous Solutions: Substitute \( x = 1 \) back into the original equation:

   \[
   \sqrt{2 - 1} = \sqrt{1} = 1
   \]

   The solution \( x = 1 \) is valid.

Example 2: Solve \( \sqrt{2 - x} = x - 1 \)

1. Isolate the Square Root: The square root is already isolated.
2. Square Both Sides:

   \[
   (\sqrt{2 - x})^2 = (x - 1)^2
   \]

   \[
   2 - x = (x - 1)^2
   \]

3. Simplify and Solve for \( x \): Expand and solve the resulting quadratic equation:

   \[
   2 - x = x^2 - 2x + 1
   \]

   Move all terms to one side to form a quadratic equation:
   \[
   x^2 - x + 1 - 2 = 0
   \]

   \[
   x^2 - 3x + 1 = 0
   \]

   Use the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) where \( a = 1 \), \( b = -3 \), and \( c = 1 \):
   \[
   x = \frac{3 \pm \sqrt{9 - 4}}{2}
   \]

   \[
   x = \frac{3 \pm \sqrt{5}}{2}
   \]

4. Check for Extraneous Solutions: Verify each solution by substituting back into the original equation:
   • For \( x = \frac{3 + \sqrt{5}}{2} \):

     \[
     \sqrt{2 - \frac{3 + \sqrt{5}}{2}} = \frac{3 + \sqrt{5}}{2} - 1
     \]

     \[
     \sqrt{\frac{4 - (3 + \sqrt{5})}{2}} = \frac{1 + \sqrt{5}}{2}
     \]

     Both sides simplify to the same value, confirming it as a valid solution.

   • For \( x = \frac{3 - \sqrt{5}}{2} \):

     \[
     \sqrt{2 - \frac{3 - \sqrt{5}}{2}} = \frac{3 - \sqrt{5}}{2} - 1
     \]

     \[
     \sqrt{\frac{4 - (3 - \sqrt{5})}{2}} = \frac{1 - \sqrt{5}}{2}
     \]

     Both sides simplify to the same value, confirming it as a valid solution.

By following these steps, you can effectively solve equations involving \( \sqrt{2 - x} \) and verify the solutions within the domain of the function.

The function \( \sqrt{2 - x} \) appears in several mathematical contexts, demonstrating its versatility and importance. Below, we explore some of its key applications.

1. Solving Inequalities:

The function \( \sqrt{2 - x} \) can be used to solve inequalities involving square roots. For example, to solve \( \sqrt{2 - x} \geq 1 \), follow these steps:

1. Square both sides of the inequality:

   \[
   (\sqrt{2 - x})^2 \geq 1^2
   \]

   \[
   2 - x \geq 1
   \]

2. Simplify and solve for \( x \):

   \[
   2 - 1 \geq x
   \]

   \[
   1 \geq x
   \]

   Thus, \( x \leq 1 \).

2. Integration:

The function \( \sqrt{2 - x} \) is often integrated in calculus problems. For instance, to find the integral of \( \sqrt{2 - x} \), use substitution:

1. Let \( u = 2 - x \), then \( du = -dx \).
2. Rewrite the integral:

   \[
   \int \sqrt{2 - x} \, dx = \int \sqrt{u} \cdot (-du) = -\int u^{1/2} \, du
   \]

3. Integrate using the power rule:

   \[
   -\int u^{1/2} \, du = -\frac{2}{3} u^{3/2} + C
   \]

4. Substitute back \( u = 2 - x \):

   \[
   -\frac{2}{3} (2 - x)^{3/2} + C
   \]

3. Differential Equations:

The function \( \sqrt{2 - x} \) can also appear in differential equations. Consider the differential equation:
\p>\[
\frac{dy}{dx} = \sqrt{2 - x}
\]

1. Separate the variables:

   \[
   dy = \sqrt{2 - x} \, dx
   \]

2. Integrate both sides:

   \[
   y = -\frac{2}{3} (2 - x)^{3/2} + C
   \]

4. Physics and Engineering:

The function \( \sqrt{2 - x} \) can model various physical phenomena, such as the displacement of an object under a specific force. For example, if the force applied to an object varies as \( \sqrt{2 - x} \), we can analyze its motion using this function.

5. Probability and Statistics:

In probability and statistics, \( \sqrt{2 - x} \) might be used in distribution functions or to transform variables. For example, if \( X \) is a random variable, \( \sqrt{2 - X} \) could represent a derived variable with specific applications in statistical models.

Understanding the various applications of \( \sqrt{2 - x} \) across different mathematical contexts enhances our ability to solve complex problems and apply mathematical concepts effectively.

When dealing with the square root of \(2-x\), several common mistakes and misconceptions can arise, leading to errors in understanding and application. Here are some key points to consider:

1. Forgetting the Domain: One common mistake is forgetting to consider the domain of the function. Since the square root of a negative number is undefined in the real number system, it's crucial to ensure that the expression inside the square root is non-negative. Therefore, the domain of \(2-x\) must be restricted appropriately to avoid such errors.
2. Ignoring the Negative Sign: Another common misconception is neglecting the negative sign in the expression \(2-x\). It's essential to recognize that this negative sign affects the behavior of the function, particularly when determining its domain, range, and graphical representation.
3. Incorrect Simplification: Sometimes, individuals may attempt to simplify the expression \(2-x\) without considering the context or constraints. This can lead to errors in solving equations or misunderstanding the properties of the function. It's crucial to apply simplification techniques cautiously, ensuring that the integrity of the expression is maintained.
4. Confusion with Square Roots: Confusion may arise when individuals mix up the properties of square roots with those of the entire expression \(2-x\). It's essential to distinguish between the square root function and the expression being evaluated within it to avoid erroneous conclusions or calculations.
5. Overlooking Restrictions: Finally, overlooking the restrictions on the variable \(x\) can lead to incorrect interpretations or solutions. It's vital to consider any implicit or explicit restrictions on \(x\) to ensure that the function is properly defined and analyzed within its applicable domain.

By being aware of these common mistakes and misconceptions, you can enhance your understanding of the square root of \(2-x\) and improve your ability to work with this mathematical expression accurately.

Exploring advanced topics and extensions related to the square root of \(2-x\) can deepen your understanding and open doors to new mathematical insights. Here are some advanced concepts to consider:

1. Complex Analysis: Delving into complex analysis allows for a deeper exploration of functions involving square roots, including those with complex inputs. By extending the domain to the complex plane, you can analyze the behavior of the square root of \(2-x\) in a broader context, uncovering fascinating properties and relationships.
2. Function Composition: Investigating the composition of functions involving the square root of \(2-x\) can lead to interesting results and insights. By combining the square root function with other functions, such as polynomials or trigonometric functions, you can study the behavior of composite functions and explore how they interact with each other.
3. Limit Analysis: Studying the limits of functions containing the square root of \(2-x\) provides valuable information about their behavior near certain points or as the input approaches specific values. Analyzing the limit as \(x\) approaches certain values or infinity can reveal important characteristics of the function, such as its asymptotic behavior or discontinuities.
4. Numerical Methods: Utilizing numerical methods, such as iterative algorithms or numerical integration, can help approximate solutions or evaluate the behavior of the square root of \(2-x\) in scenarios where analytical methods may be impractical. By employing numerical techniques, you can gain insights into the behavior of the function across a wide range of inputs.
5. Applications in Physics and Engineering: Exploring applications of the square root of \(2-x\) in physics and engineering contexts can showcase its relevance and practical significance. From modeling physical phenomena to solving engineering problems, understanding the properties and behavior of this function can have profound implications in various real-world scenarios.

By delving into these advanced topics and extensions, you can deepen your knowledge of the square root of \(2-x\) and its broader implications in mathematics and beyond.

Practice problems are an excellent way to reinforce your understanding of the square root of \(2-x\) and sharpen your problem-solving skills. Here are some practice problems along with their solutions:

1. Problem 1: Determine the domain of the function \(f(x) = \sqrt{2-x}\).

   Solution: To find the domain, we need to ensure that the expression inside the square root is non-negative. Thus, we have:

   \(2-x \geq 0\)	Given
   \(2 \geq x\)	Add \(x\) to both sides
   \(x \leq 2\)	Subtract 2 from both sides

   Therefore, the domain of the function \(f(x) = \sqrt{2-x}\) is \(x \leq 2\).

2. Problem 2: Solve the equation \(\sqrt{2-x} = 3\).

   Solution: To solve the equation, we square both sides to eliminate the square root:

   \(\sqrt{2-x} = 3\)	Given
   \((\sqrt{2-x})^2 = 3^2\)	Square both sides
   \(2-x = 9\)	Simplify
   \(x = -7\)	Isolate \(x\)

   Therefore, the solution to the equation \(\sqrt{2-x} = 3\) is \(x = -7\).

3. Problem 3: Sketch the graph of the function \(f(x) = \sqrt{2-x}\).

   Solution: To sketch the graph, we'll plot points and determine the behavior of the function:

   • Choose values for \(x\) and calculate the corresponding \(f(x)\).
   • Plot the points on the coordinate plane.
   • Observe the behavior of the function as \(x\) approaches different values.

   By following these steps, you can sketch the graph of the function \(f(x) = \sqrt{2-x}\).

Practice these problems to enhance your understanding and proficiency in working with the square root of \(2-x\), and check your solutions to ensure accuracy.

Explore further reading materials and resources to deepen your knowledge of the square root of \(2-x\) and related topics:

• : This comprehensive guide provides a detailed explanation of square roots, including properties, simplification techniques, and examples.
• : Dive into Khan Academy's extensive collection of lessons and exercises covering rational exponents, radicals, and square roots to strengthen your understanding.
• : Watch this informative video for an introduction to square roots, their properties, and how to work with them effectively.
• : Use Wolfram Alpha to compute the square root of \(2-x\) and explore its properties, graphs, and additional information.
• : Practice solving algebraic problems, including those involving square roots, using Mathway's powerful problem-solving tool.

These resources offer valuable insights, explanations, and practice opportunities to enhance your understanding and mastery of the square root of \(2-x\) and its applications.