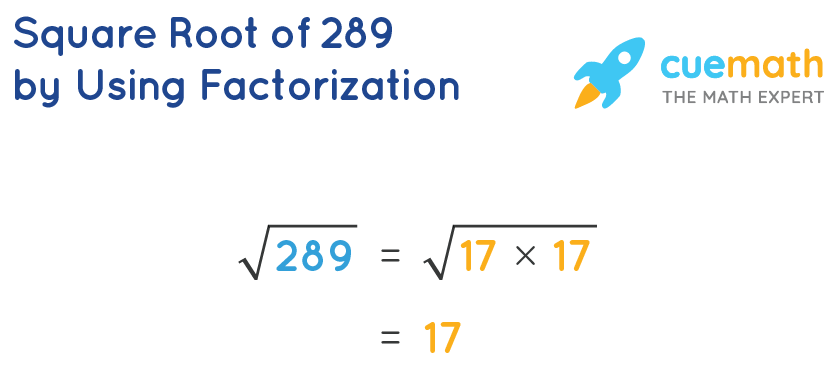Topic what's the square root of 24: The square root of 24, denoted as √24, is approximately 4.89898. This number is irrational, meaning it cannot be expressed as a simple fraction. In this guide, we will explore various methods to calculate it, its applications, and interesting facts related to the square root of 24.
Table of Content
- Square Root of 24
- Introduction to Square Root of 24
- Definition and Basic Concept
- Decimal Representation
- Prime Factorization Method
- Long Division Method
- Using Calculators for Square Root
- Applications of Square Root of 24
- Geometric Applications
- Mathematical Applications
- Engineering Applications
- Computer Science Applications
- Rational Approximations
- Irrational Numbers and Their Properties
- Further Reading and Resources
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai của 24 (Sqrt(24)) để giúp bạn hiểu rõ hơn về khái niệm này.
Square Root of 24
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 24 can be found using different methods, and it is an irrational number, meaning it cannot be expressed as a simple fraction.
Decimal Form
The square root of 24 in decimal form is approximately:
\(\sqrt{24} \approx 4.89898\)
Simplified Radical Form
In its simplified radical form, the square root of 24 is expressed as:
\(\sqrt{24} = 2\sqrt{6}\)
Calculation Methods
- Prime Factorization: By breaking down 24 into its prime factors (2 x 2 x 2 x 3), we can simplify the square root of 24 as \(2\sqrt{6}\).
- Long Division Method: This method involves a step-by-step approach to manually calculate the square root, yielding a result close to 4.89898.
- Using a Calculator: Most calculators have a square root function that can quickly provide an approximate value.
Applications
The square root of 24, like other square roots, is used in various fields such as mathematics, physics, engineering, and computer science. It is often encountered in problems involving areas, volumes, and other geometric calculations.
Interesting Facts
- The square root of a non-perfect square (like 24) is always an irrational number.
- Rational approximations of \(\sqrt{24}\) can be used for practical purposes, such as 4.9 or 5.
- The simplified form \(2\sqrt{6}\) shows the relationship between the factors of 24 and helps in understanding the properties of square roots better.
Conclusion
Understanding the square root of 24 involves recognizing its decimal and radical forms, and it highlights the importance of square roots in mathematical computations and practical applications.

READ MORE:
Introduction to Square Root of 24
The square root of 24, represented as √24, is a number that, when multiplied by itself, equals 24. This value is approximately 4.89898, making it an irrational number because it cannot be expressed as a simple fraction. Understanding the square root of 24 involves exploring its decimal representation, simplified radical form, and calculation methods.
Here's a step-by-step breakdown of key concepts related to the square root of 24:
- Decimal Representation: √24 ≈ 4.89898. This is the approximate value you get when calculating the square root using a calculator or long division method.
- Simplified Radical Form: √24 can be simplified to 2√6. This involves breaking down 24 into its prime factors and simplifying the radical expression.
- Prime Factorization Method: By expressing 24 as the product of its prime factors (2 × 2 × 2 × 3), we can rewrite √24 as 2√6.
- Long Division Method: This method allows for a more precise calculation of √24, breaking it down step-by-step to achieve an accurate decimal result.
In the sections that follow, we will delve deeper into each of these concepts, providing a comprehensive guide to understanding and working with the square root of 24.
Definition and Basic Concept
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 24 is denoted as √24.
The square root of 24 can be represented in different forms:
- Decimal form: The approximate value of √24 is 4.899.
- Simplified radical form: The simplified form of √24 is 2√6.
- Exponent form: It can also be written as 241/2.
To understand this concept, consider the following steps:
- Radical symbol (√): The symbol '√' represents the square root.
- Radicand: The number inside the radical symbol is called the radicand. Here, 24 is the radicand.
- Square root properties: The square root of a non-perfect square is an irrational number. Therefore, √24 is an irrational number.
Mathematically, the square root function reverses the squaring of a number:
If √24 = x, then x2 = 24.
Since 24 is not a perfect square, its square root is not an integer. The simplest radical form and the decimal representation help in understanding the value of √24 better.
| Method | Result |
| Decimal Form | 4.899 |
| Radical Form | 2√6 |
| Exponent Form | 241/2 |
By understanding these representations and properties, you can grasp the basic concept of the square root of 24.
Decimal Representation
The square root of 24 is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal representation is a non-terminating and non-repeating decimal. The approximate value of the square root of 24 is:
\[
\sqrt{24} \approx 4.898979485566356
\]
Here is a more detailed breakdown of the decimal representation:
- The first digit after the decimal is 8.
- The second digit is 9.
- The third digit is 8.
- The fourth digit is 9.
- The fifth digit is 7.
- The sixth digit is 9.
- The seventh digit is 4.
- The eighth digit is 8.
You can continue this pattern to get more precise values. Calculators and computer software typically handle the calculations to a high degree of precision.
For most practical purposes, the value \(\sqrt{24} \approx 4.899\) is used. This level of precision is sufficient for most applications in engineering, physics, and mathematics.
Prime Factorization Method
The prime factorization method is a useful way to find the square root of a number by breaking it down into its prime factors. Let's go through the steps to find the square root of 24 using this method:
- Find the prime factors of 24.
- 24 = 2 × 2 × 2 × 3
- Pair similar prime factors.
- 24 = 2² × 2 × 3
- Take the square root of each pair and multiply them.
- \(\sqrt{24} = \sqrt{2^2 \times 2 \times 3} = 2 \times \sqrt{6}\)
- Simplify the result.
- \(\sqrt{24} \approx 2 \times 2.449 \approx 4.898\)
Therefore, the square root of 24, using the prime factorization method, is approximately 4.898.
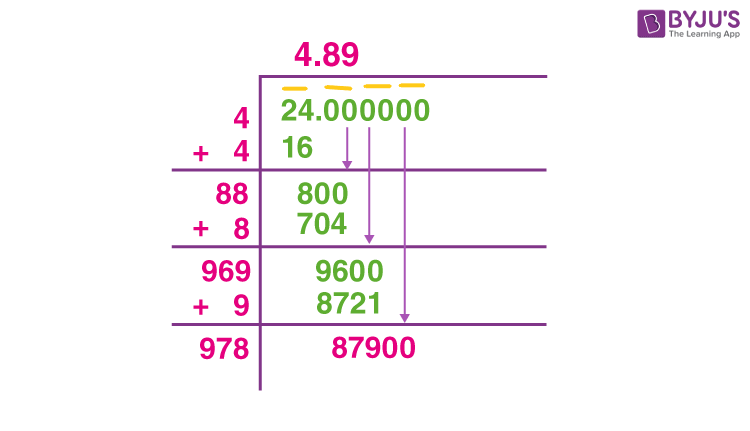
Long Division Method
The long division method is a manual technique to find the square root of a number. Here is a step-by-step guide to find the square root of 24 using this method:
First, pair the digits of the number from right to left. Since 24 has only two digits, it remains as 24.
Find the largest number whose square is less than or equal to the first pair. The largest number whose square is less than 24 is 4, because \(4^2 = 16\). Write 4 as the first digit of the square root.
Subtract the square of 4 from the first pair: 24 - 16 = 8. Bring down the next pair of digits (in this case, 00, because we have no more digits). Now we have 800.
Double the number already found in the quotient (4), which gives us 8. Write this number as a divisor, leaving a blank space next to it: 8_. Now we need to find a digit (X) such that \(8X \times X \leq 800\).
Try 8: \(88 \times 8 = 704\), which is less than 800. So, we write 8 in the quotient, giving us 4.8.
Subtract \(704\) from \(800\), leaving a remainder of 96. Bring down another pair of zeros, making it 9600.
Double the part of the quotient found so far (48), giving us 96. Write this as the new divisor, leaving a blank space: 960_. Find a digit (Y) such that \(960Y \times Y \leq 9600\).
Try 9: \(9609 \times 9 = 86481\), which is too large. Try 8: \(9608 \times 8 = 76864\), which is less than 9600. Write 8 in the quotient, giving us 4.88.
Subtract \(76864\) from \(9600\), leaving a remainder. Repeat the process to get more decimal places as needed.
Therefore, the square root of 24 using the long division method is approximately 4.88, accurate to two decimal places. Continue the process to obtain more precise values.
Using Calculators for Square Root
Calculators are a quick and efficient tool for finding the square root of a number. Here is a step-by-step guide to using a calculator to find the square root of 24:
Turn on your calculator and ensure it is in the correct mode for calculating square roots. Most calculators have a specific button for square root, often represented by the symbol \(\sqrt{}\) or the abbreviation "sqrt".
Enter the number 24 into the calculator. This can be done by pressing the digits 2 and 4 in sequence.
Press the square root button (\(\sqrt{}\) or "sqrt"). On many calculators, this will immediately display the square root of the entered number. If your calculator requires an additional step, you might need to press the "=" or "Enter" button.
Read the result displayed on the calculator screen. The square root of 24 will be shown as approximately 4.89898. This is a rounded decimal representation.
For more precision, you can use a scientific calculator or an online calculator that allows for more decimal places. Many online calculators also provide the option to view the result in different formats, such as fractional or exponential forms.
Using a calculator to find the square root of 24 is a straightforward process that provides an accurate and quick result. This method is especially useful for confirming manual calculations or when a precise decimal value is required.
Applications of Square Root of 24
The square root of 24, approximately 4.899, has several practical applications across different fields. Here are some key applications:
Geometric Applications
In geometry, the square root of 24 can be used to determine the lengths of sides in right triangles and other geometric figures. For example, if one side of a right triangle is √24, it helps in calculating the hypotenuse or the other side using the Pythagorean theorem.
Mathematical Applications
In mathematics, √24 is useful for solving quadratic equations where the solutions involve square roots. It's also applied in algebraic operations and calculus, especially when working with functions involving radicals.
Engineering Applications
Engineers often encounter √24 in calculations related to stress and strain in materials, electrical circuits, and fluid dynamics. For instance, in structural engineering, it might be part of formulas used to compute load distributions.
Computer Science Applications
In computer science, the square root of 24 can be relevant in algorithms that involve geometric computations, graphics rendering, and optimizations. It's also used in machine learning algorithms for normalization and data transformation.
Practical Examples
- Calculating the diagonal of a rectangle: If a rectangle has sides of length 6 and 4, the diagonal can be found using the square root of the sum of the squares of the sides, which involves √24.
- Physics problems: √24 can appear in formulas for calculating distances, velocities, and other physical properties where square roots are involved.
- Financial modeling: In some complex financial models, square roots of numbers, including √24, can appear in formulas for risk assessment and predictions.
These applications highlight the versatility and importance of understanding the square root of 24 in various scientific and practical contexts.
Geometric Applications
The square root of 24 has several interesting applications in geometry. Below, we explore some key examples:
1. Calculating the Length of a Diagonal
In a rectangle, the diagonal can be found using the Pythagorean theorem. If one side is \( a \) and the other side is \( b \), the diagonal \( d \) is given by:
\[
d = \sqrt{a^2 + b^2}
\]
Consider a rectangle with sides 4 and 2√6. The diagonal is:
\[
d = \sqrt{4^2 + (2\sqrt{6})^2} = \sqrt{16 + 24} = \sqrt{40} = 2\sqrt{10}
\]
2. Area of an Equilateral Triangle
The area \( A \) of an equilateral triangle with side length \( s \) can be calculated using:
\[
A = \frac{\sqrt{3}}{4} s^2
\]
If the side length is \( 2\sqrt{6} \), the area is:
\[
A = \frac{\sqrt{3}}{4} (2\sqrt{6})^2 = \frac{\sqrt{3}}{4} \times 24 = 6\sqrt{3}
\]
3. Volume of a Cube
The volume \( V \) of a cube with side length \( s \) is given by:
\[
V = s^3
\]
If the side length is \( \sqrt{24} \), the volume is:
\[
V = (\sqrt{24})^3 = 24\sqrt{24}
\]
4. Constructing Right-Angled Triangles
The square root of 24 is useful in constructing right-angled triangles. If one leg of a right-angled triangle is \( \sqrt{24} \) and the other is 6, the hypotenuse \( c \) is:
\[
c = \sqrt{(\sqrt{24})^2 + 6^2} = \sqrt{24 + 36} = \sqrt{60} = 2\sqrt{15}
\]
5. Inscribing a Circle in a Square
If a circle is inscribed in a square with an area of 24 square units, the diameter of the circle is the side length of the square. Thus, the side length \( s \) is:
\[
s = \sqrt{24}
\]
Hence, the radius \( r \) of the circle is:
\[
r = \frac{\sqrt{24}}{2}
\]
These examples illustrate the versatility of the square root of 24 in various geometric contexts, enhancing our understanding of shapes, areas, and volumes.

Mathematical Applications
The square root of 24, approximately 4.89897948557, has various mathematical applications. Below are some key areas where the square root of 24 is commonly used:
-
Solving Quadratic Equations:
In quadratic equations, the square root of 24 might appear as part of the solution. For example, in an equation of the form \(x^2 = 24\), solving for \(x\) involves taking the square root of both sides to yield \(x = \pm \sqrt{24}\).
-
Geometry:
The square root of 24 is useful in various geometric problems, particularly those involving right triangles. For instance, if the lengths of two legs of a right triangle are given, and one of the legs is \(2\sqrt{6}\), then this leg's length squared is 24.
-
Trigonometry:
In trigonometry, the square root of 24 can be used to simplify the calculations of trigonometric functions, particularly when dealing with expressions under a square root sign. For example, simplifying expressions such as \(\sin(\theta) = \frac{\sqrt{24}}{5}\).
-
Calculus:
In calculus, the square root of 24 can appear in various contexts, such as in the computation of integrals and derivatives where the function involves square roots. For example, integrating a function like \(\int \sqrt{24} \, dx\) will require recognizing and simplifying the square root of 24.
-
Algebra:
In algebra, the square root of 24 may be used in simplifying expressions, solving equations, and working with radical equations. For instance, simplifying \( \sqrt{24} \cdot \sqrt{6} \) into \( \sqrt{144} = 12 \).
Overall, the square root of 24 is an important value in many mathematical fields and problem-solving scenarios, providing a basis for further calculations and simplifications.
Engineering Applications
The square root of 24, approximately 4.898, has various engineering applications. Understanding and utilizing this value can be crucial in fields such as structural engineering, electrical engineering, and mechanical design.
1. Structural Engineering
In structural engineering, the square root of 24 can be used to determine load distributions and material strengths. For example, calculating the side length of a square with an area of 24 square units involves the square root:
\[
\text{Side length} = \sqrt{24} \approx 4.898
\]
This is important when designing components that must fit within specific spatial constraints.
2. Electrical Engineering
Electrical engineers often encounter situations where the square root of 24 is useful, especially in impedance calculations in AC circuits. Impedance, which combines resistance and reactance, can be expressed in terms of square roots for simplified calculations:
\[
Z = \sqrt{R^2 + X^2}
\]
If R and X are such that their sum of squares equals 24, the impedance can be directly linked to \(\sqrt{24}\).
3. Mechanical Design
In mechanical design, particularly in the optimization of mechanical systems, the square root of 24 can help in determining the dimensions of components that must comply with design specifications involving areas or volumes. For instance:
\[
\text{If a design requires a component with a volume of } 24 \text{ cubic units, the side length of a cubic component is } \sqrt[3]{24}.
\]
4. Thermal Engineering
Thermal engineers use the square root of 24 in calculations involving heat transfer and thermal conductivity. For example, in solving problems related to the heat equation, the square root function often appears:
\[
\Delta T = k \sqrt{A}
\]
Where \( A = 24 \) could represent the area through which heat is transferred.
5. Fluid Dynamics
In fluid dynamics, the square root of 24 might appear in the calculation of flow rates and velocities, especially in turbulent flow where square root functions are common:
\[
v = k \sqrt{gh}
\]
If certain conditions simplify to the form \( k \sqrt{24} \), understanding this root is crucial for accurate computations.
By applying the square root of 24 in these contexts, engineers can solve complex problems more effectively and design more efficient systems.
Computer Science Applications
The square root of 24, approximately 4.89898, has various applications in computer science, especially in fields that require precise calculations and optimizations. Here are some key areas where the square root of 24 is relevant:
-
Algorithm Design: Many algorithms, particularly those involving search and sort operations, use the square root in their complexity analysis. For example, certain divide-and-conquer algorithms break down problems into subproblems whose size is a square root of the original problem.
-
Cryptography: In cryptography, the security of algorithms often relies on mathematical principles, including square roots. The square root function is used in various encryption and decryption processes.
-
Computer Graphics: Calculating distances between points in 3D space often involves square roots. For example, the distance formula in a 3-dimensional coordinate system uses the square root of the sum of the squared differences of the coordinates.
-
Machine Learning: In machine learning, particularly in the context of optimization algorithms like gradient descent, the calculation of Euclidean distances involves square roots. This is crucial for algorithms that minimize the distance between points in high-dimensional space.
-
Data Structures: Some advanced data structures like sqrt-decomposition use square roots to optimize query and update operations, balancing the trade-off between time complexity and space usage.
In these applications, the precise value of the square root of 24 is often used in computations to achieve accurate results, highlighting the importance of mathematical constants in computer science.
Rational Approximations
Approximating the square root of 24 using rational numbers can be helpful when an exact value is not necessary or when working without a calculator. Here are some methods to find rational approximations for the square root of 24:
Method 1: Using Perfect Squares
To find a rational approximation, we can start by identifying perfect squares close to 24:
- The perfect square less than 24 is \(4^2 = 16\)
- The perfect square greater than 24 is \(5^2 = 25\)
Thus, we know that:
\[ 4 < \sqrt{24} < 5 \]
Method 2: Averaging Method
We can refine the approximation by averaging numbers within the interval:
- Start with the interval [4, 5]
- Calculate the midpoint: \(\frac{4 + 5}{2} = 4.5\)
- Square the midpoint: \(4.5^2 = 20.25\)
- Since \(20.25 < 24\), the square root of 24 is closer to 5 than to 4.5
Next, refine the interval [4.5, 5]:
- Midpoint: \(\frac{4.5 + 5}{2} = 4.75\)
- Square the midpoint: \(4.75^2 = 22.5625\)
- Since \(22.5625 < 24\), the square root of 24 is closer to 5 than to 4.75
Continue this process to get more accurate approximations.
Method 3: Using the Formula for Better Approximation
Another method involves using a formula to approximate square roots:
Let \( n = 24 \), \( p = 16 \) (largest perfect square less than 24), and \( q = 8 \) (since \( 24 - 16 = 8 \)). The formula is:
\[\sqrt{n} \approx \sqrt{p} + \frac{q}{2\sqrt{p} + 1}\]
Substitute the values:
\[\sqrt{24} \approx 4 + \frac{8}{2(4) + 1} = 4 + \frac{8}{9} \approx 4 + 0.89 \approx 4.89\]
Thus, a rational approximation for the square root of 24 is approximately 4.89.
Decimal Approximations
Using decimal approximations, we often round to a certain number of decimal places. The square root of 24 is approximately 4.898979485. For practical purposes, it can be rounded to:
- 1 decimal place: 4.9
- 2 decimal places: 4.90
- 3 decimal places: 4.899
These methods provide ways to find rational approximations for the square root of 24, which can be useful in various mathematical calculations and applications.

Irrational Numbers and Their Properties
An irrational number is a real number that cannot be expressed as a ratio of two integers. This means it cannot be written in the form p/q, where p and q are integers and q ≠ 0. The square root of 24, denoted as
Irrational numbers have several key properties:
- Non-terminating and Non-repeating Decimal Expansion: The decimal form of an irrational number never ends and does not repeat in a pattern. For instance, the decimal representation of
\(\sqrt{24}\) is approximately 4.898979485566356, and it continues without repeating. - Inclusion in the Real Number System: Irrational numbers are part of the real numbers. Together with rational numbers, they complete the set of real numbers, denoted as
\(\mathbb{R}\) . - Algebraic and Transcendental Types: Irrational numbers can be classified as algebraic or transcendental. Algebraic irrationals are roots of non-zero polynomial equations with rational coefficients, such as
\(\sqrt{24}\) . Transcendental numbers, like π and e, are not roots of any such polynomial. - Closure Under Addition and Multiplication: The sum or product of a rational number and an irrational number is irrational. However, the sum or product of two irrational numbers can be rational or irrational.
Understanding these properties helps in various fields of mathematics and practical applications where precise calculations are essential.
Further Reading and Resources
For those looking to expand their knowledge about square roots and their applications, here are some valuable resources and topics to explore:
- Mathematical Textbooks:
- Introduction to Algebra - This textbook covers the fundamental concepts of algebra, including the properties and operations involving square roots.
- Pre-Calculus Mathematics - A comprehensive resource that delves into more complex applications of square roots in trigonometry and calculus.
- Online Educational Platforms:
- - Offers free lessons and practice problems on radicals and square roots.
- - Provides courses that include modules on algebraic expressions and square roots.
- Research Papers and Articles:
- - An academic paper discussing the theory and applications of square roots in various fields.
- - An in-depth article exploring different methods to calculate and use the square root of 24.
- Mathematics Software and Tools:
- - A computational engine that can provide detailed solutions and visualizations for square roots.
- - An online tool for plotting and exploring functions involving square roots.
- Video Tutorials:
- - A YouTube tutorial explaining the concept of square roots and how to calculate them.
- - A step-by-step guide on simplifying square roots, including examples and practice problems.
These resources provide a comprehensive foundation for understanding and applying the concept of square roots. Whether you are a student, educator, or enthusiast, these materials will enhance your knowledge and skills in mathematics.
Video hướng dẫn cách đơn giản hóa căn bậc hai của 24 (Sqrt(24)) để giúp bạn hiểu rõ hơn về khái niệm này.
Cách Đơn Giản Hóa Căn Bậc Hai Của 24: Sqrt(24)
READ MORE:
Video hướng dẫn về căn bậc hai của 24 để giúp bạn hiểu rõ hơn về khái niệm này.
Căn Bậc Hai Của 24