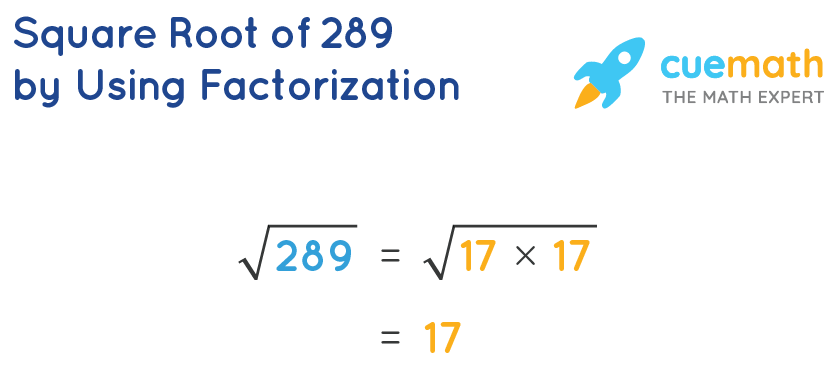Topic whats the square root of 225: Curious about the square root of 225? You're in the right place! In this article, we'll not only reveal the answer but also explore how understanding this fundamental concept can be applied in various real-life scenarios and mathematical problems. Dive in to enhance your knowledge and see the importance of square roots in action.
Table of Content
- Square Root of 225
- Introduction
- Definition of Square Root
- Calculation of the Square Root of 225
- Mathematical Explanation
- Prime Factorization Method
- Perfect Squares and Their Properties
- Applications of Square Roots
- Visual Representation of Square Roots
- Common Misconceptions about Square Roots
- Practice Problems and Solutions
- Advanced Topics: Square Roots in Algebra
- Square Roots in Geometry
- Square Roots in Real-Life Scenarios
- Conclusion
- YOUTUBE:
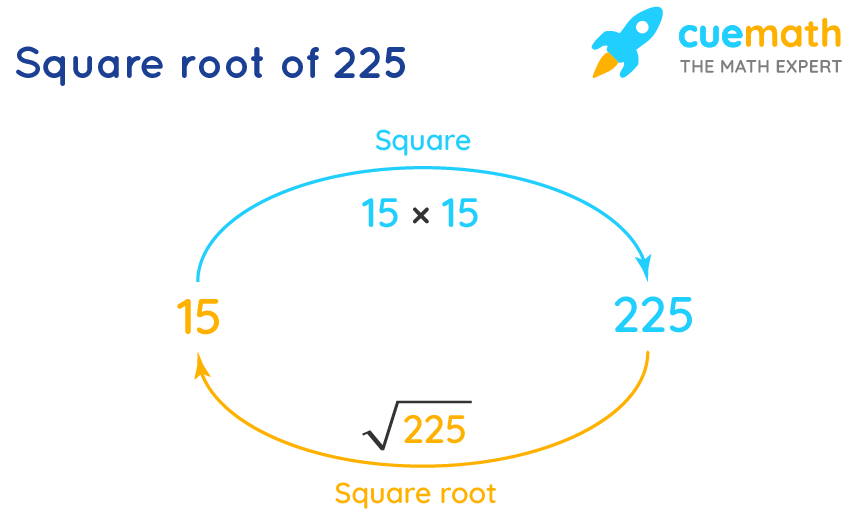
Square Root of 225
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, the square root of 225 is the number which, when squared, equals 225.
Calculation
The square root of 225 is calculated as follows:
\(\sqrt{225} = 15\)
This means:
\(15 \times 15 = 225\)
Explanation
Here is a detailed explanation of the process to find the square root of 225:
- First, identify the factors of 225. They are 1, 3, 5, 9, 15, 25, 45, 75, and 225.
- Notice that 15 is a factor of 225.
- When you multiply 15 by itself (15 * 15), you get 225.
Applications
Understanding square roots is essential in various fields, including:
- Mathematics: solving quadratic equations.
- Engineering: calculating areas and volumes.
- Physics: working with wave functions and quantum mechanics.
Visual Representation
The square root of 225 can also be represented visually:
| Original Number | Square Root | Verification |
| 225 | 15 | \(15 \times 15 = 225\) |
Therefore, the square root of 225 is 15, which is a perfect square.

READ MORE:
Introduction
The concept of square roots is fundamental in mathematics, providing a foundation for various advanced topics. Understanding the square root of a number, such as 225, helps in solving mathematical problems and real-life applications. The square root of a number is a value that, when multiplied by itself, gives the original number. In this section, we will explore the basics of square roots, the calculation of the square root of 225, and its significance in different contexts.
The square root of 225 is denoted as \(\sqrt{225}\). This can be expressed mathematically as:
\(\sqrt{225} = 15\)
Here's a step-by-step explanation of how to determine the square root of 225:
- Identify the factors of 225: These include 1, 3, 5, 9, 15, 25, 45, 75, and 225.
- Among these factors, find the pair of numbers that when multiplied together result in 225. Notice that 15 is one of these factors.
- Verify by calculating: \(15 \times 15 = 225\), thus confirming that the square root of 225 is indeed 15.
The calculation can also be represented in a simple table:
| Number | Square Root | Verification |
| 225 | 15 | \(15 \times 15 = 225\) |
Understanding the square root of 225 is not just a mathematical exercise but also has practical applications in fields such as engineering, physics, and computer science. By mastering square roots, you lay the groundwork for tackling more complex mathematical challenges and real-world problems.
Definition of Square Root
A square root of a number is a value that, when multiplied by itself, yields the original number. Mathematically, if \( x \) is the square root of \( y \), then \( x^2 = y \). The square root is represented by the radical symbol \( \sqrt{} \).
For example, the square root of 225 can be expressed as:
\(\sqrt{225} = 15\)
Here’s a step-by-step explanation of the square root concept:
- Identify the original number (in this case, 225).
- Find a number which, when multiplied by itself, equals the original number.
- Verify the calculation: \( 15 \times 15 = 225 \).
Square roots can be categorized into two types:
- Perfect Square Roots: These are roots of perfect squares, numbers which are squares of integers. For example, 225 is a perfect square because 15 is an integer and \( 15^2 = 225 \).
- Irrational Square Roots: These are roots of numbers that are not perfect squares. The result is an irrational number. For example, the square root of 2 is approximately 1.41421356, which cannot be expressed as a precise fraction.
The square root function is essential in various mathematical contexts, including solving quadratic equations, simplifying expressions, and analyzing geometric properties. It also plays a significant role in different fields such as physics, engineering, and computer science.
The following table summarizes key points about the square root of 225:
| Original Number | Square Root | Verification |
| 225 | 15 | \( 15 \times 15 = 225 \) |
By understanding the definition and properties of square roots, we can apply this knowledge to solve practical problems and appreciate the elegance of mathematical concepts.
Calculation of the Square Root of 225
Calculating the square root of a number involves finding a value that, when multiplied by itself, gives the original number. The square root of 225 can be calculated in a straightforward manner since it is a perfect square. Here’s a step-by-step method to find the square root of 225:
- Identify the Original Number: The number in question is 225.
- Prime Factorization Method: Break down 225 into its prime factors:
- 225 is divisible by 5: \( 225 \div 5 = 45 \)
- 45 is divisible by 5: \( 45 \div 5 = 9 \)
- 9 is divisible by 3: \( 9 \div 3 = 3 \)
- 3 is a prime number.
- Pair the Prime Factors: Group the prime factors into pairs:
- \( (5 \times 5) \) and \( (3 \times 3) \).
- Take One Factor from Each Pair: From each pair of prime factors, take one number:
- \( 5 \) from \( (5 \times 5) \) and \( 3 \) from \( (3 \times 3) \).
- Multiply the Selected Factors: Multiply these numbers together to find the square root:
- \( 5 \times 3 = 15 \).
- Verification: Confirm the result by squaring it:
- \( 15 \times 15 = 225 \).
Thus, the square root of 225 is \( 15 \).
The calculation can be summarized in the following table:
| Step | Description | Result |
| 1 | Identify the original number | 225 |
| 2 | Prime factorization | \( 5^2 \times 3^2 \) |
| 3 | Pair the prime factors | \( (5 \times 5) \) and \( (3 \times 3) \) |
| 4 | Take one factor from each pair | 5 and 3 |
| 5 | Multiply the selected factors | 15 |
| 6 | Verification | \( 15 \times 15 = 225 \) |
By following these steps, we can easily determine that the square root of 225 is \( 15 \), demonstrating the simplicity and elegance of mathematical calculations.
Mathematical Explanation
The square root of a number is a value that, when multiplied by itself, results in the original number. Mathematically, if \( x \) is the square root of \( y \), then \( x^2 = y \). To find the square root of 225, we need to determine which number squared equals 225. Here’s a detailed mathematical explanation:
- Start with the Definition: The square root of 225 is a number that satisfies the equation:
\( x^2 = 225 \)
- Prime Factorization: Break down 225 into its prime factors:
- 225 is divisible by 5: \( 225 \div 5 = 45 \)
- 45 is divisible by 5: \( 45 \div 5 = 9 \)
- 9 is divisible by 3: \( 9 \div 3 = 3 \)
- 3 is a prime number.
\( 225 = 5 \times 5 \times 3 \times 3 = 5^2 \times 3^2 \)
- Group the Prime Factors: Pair the prime factors to find the square root:
- \( 5^2 \) and \( 3^2 \)
- Extract the Square Root: Take one factor from each pair:
- \( \sqrt{5^2} = 5 \)
- \( \sqrt{3^2} = 3 \)
- Multiply the Results: Multiply these results to get the square root of 225:
\( 5 \times 3 = 15 \)
- Verification: Verify the result by squaring it:
\( 15 \times 15 = 225 \)
This confirms that the square root of 225 is indeed 15. The calculation can be summarized in the following table:
| Step | Description | Result |
| 1 | Identify the original number | 225 |
| 2 | Prime factorization | \( 5^2 \times 3^2 \) |
| 3 | Pair the prime factors | \( (5 \times 5) \) and \( (3 \times 3) \) |
| 4 | Take one factor from each pair | 5 and 3 |
| 5 | Multiply the selected factors | 15 |
| 6 | Verification | \( 15 \times 15 = 225 \) |
Thus, by understanding the mathematical explanation, we see that the square root of 225 is 15, demonstrating how mathematical principles can be applied to solve for square roots.
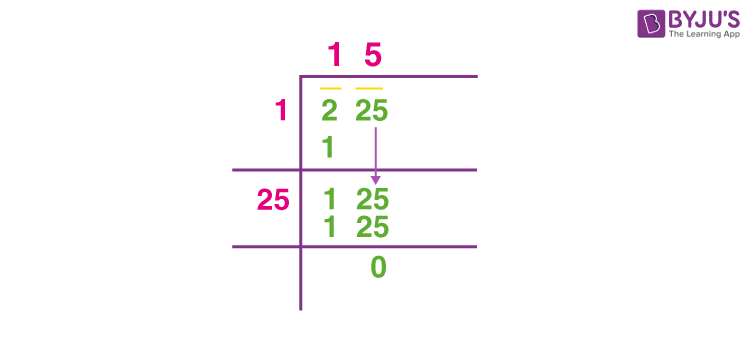
Prime Factorization Method
The prime factorization method is a systematic way of breaking down a number into its prime factors to find its square root. This method is particularly useful for perfect squares. Here’s a step-by-step explanation of how to use the prime factorization method to find the square root of 225:
- Identify the Number: The number we need to find the square root for is 225.
- Perform Prime Factorization: Break down 225 into its prime factors by dividing it by the smallest prime numbers:
- 225 is divisible by 5: \( 225 \div 5 = 45 \)
- 45 is divisible by 5: \( 45 \div 5 = 9 \)
- 9 is divisible by 3: \( 9 \div 3 = 3 \)
- 3 is a prime number.
\( 225 = 5 \times 5 \times 3 \times 3 = 5^2 \times 3^2 \)
- Group the Prime Factors: Pair the prime factors to form perfect squares:
- \( 5^2 \) and \( 3^2 \)
- Extract the Square Root: Take the square root of each pair:
- \( \sqrt{5^2} = 5 \)
- \( \sqrt{3^2} = 3 \)
- Multiply the Results: Multiply these numbers to get the square root of 225:
\( 5 \times 3 = 15 \)
- Verification: Confirm the result by squaring it:
\( 15 \times 15 = 225 \)
To summarize, the prime factorization method helps us to systematically break down the number and find its square root efficiently. Here’s a table summarizing the steps:
| Step | Description | Result |
| 1 | Identify the number | 225 |
| 2 | Prime factorization | \( 5^2 \times 3^2 \) |
| 3 | Pair the prime factors | \( 5^2 \) and \( 3^2 \) |
| 4 | Extract the square root of each pair | 5 and 3 |
| 5 | Multiply the results | 15 |
| 6 | Verification | \( 15 \times 15 = 225 \) |
By following these steps, we have determined that the square root of 225 is 15 using the prime factorization method.
Perfect Squares and Their Properties
A perfect square is a number that can be expressed as the product of an integer with itself. In mathematical terms, if \( n \) is an integer, then \( n^2 \) is a perfect square. Perfect squares have unique properties that make them interesting and useful in various fields of mathematics. Here’s a detailed explanation of perfect squares and their properties:
- Definition: A perfect square is a number that can be written as \( n^2 \), where \( n \) is an integer.
For example, 225 is a perfect square because it can be written as \( 15^2 \).
- Properties of Perfect Squares:
- Non-negative: Perfect squares are always non-negative because the product of any real number with itself is non-negative.
- Square Root: The square root of a perfect square is always an integer.
For instance, \( \sqrt{225} = 15 \).
- Number of Factors: Perfect squares have an odd number of total factors.
For example, the factors of 225 are 1, 3, 5, 9, 15, 25, 45, 75, and 225, totaling 9 factors.
- Ending Digits: In the decimal system, a perfect square can only end in specific digits (0, 1, 4, 5, 6, or 9).
225 ends in 5, making it eligible to be a perfect square.
- Sum of Odd Numbers: Every perfect square is the sum of consecutive odd numbers.
For example, \( 225 = 1 + 3 + 5 + \ldots + 29 \) (the sum of the first 15 odd numbers).
- Examples of Perfect Squares:
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- \( 10^2 = 100 \)
- \( 15^2 = 225 \)
- Applications of Perfect Squares:
- Geometry: Perfect squares are used in calculating areas of squares and other geometric shapes.
- Algebra: Solving quadratic equations often involves perfect squares.
- Number Theory: Understanding the properties of numbers and their divisibility.
Perfect squares play a crucial role in various mathematical disciplines due to their distinct properties. They provide a foundation for more complex concepts and have practical applications in different fields of study.
Applications of Square Roots
Square roots have numerous applications in various fields, ranging from everyday life to complex scientific calculations. Here are some of the primary applications of square roots:
- Geometry: Square roots are used to determine the length of the sides of right-angled triangles through the Pythagorean theorem. For example, if the lengths of the legs of a right triangle are known, the length of the hypotenuse can be calculated using the formula \( c = \sqrt{a^2 + b^2} \).
- Engineering: In engineering, square roots are essential for calculating distances, forces, and various physical properties. For instance, the formula for the period of a pendulum, \( T = 2\pi \sqrt{\frac{L}{g}} \), involves the square root of the length of the pendulum divided by the acceleration due to gravity.
- Physics: Square roots are used in various physical laws and equations. For example, the formula for kinetic energy, \( KE = \frac{1}{2}mv^2 \), involves the velocity term, which is sometimes derived from square root calculations in energy conservation problems.
- Economics: In economics and finance, the square root is used in various formulas to calculate rates of return, risks, and statistical measures. For example, the standard deviation, a measure of volatility, is the square root of the variance.
- Computer Science: Algorithms involving graphics and game development frequently use square roots. For instance, calculating the distance between two points in a 2D or 3D space requires the use of the Euclidean distance formula, \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \).
- Architecture: Architects use square roots in design and structural calculations to ensure the stability and aesthetic proportions of buildings. For example, the diagonal of a square floor plan can be calculated as \( d = \sqrt{2a^2} \) where \( a \) is the length of one side of the square.
- Medicine: Square roots are used in medical imaging and radiation therapy. For example, the inverse square law in radiation physics states that the intensity of radiation is inversely proportional to the square of the distance from the source, \( I \propto \frac{1}{d^2} \).
In summary, the concept of square roots is not only fundamental in mathematics but also critical in practical applications across various domains. Understanding how to calculate and apply square roots enables solving real-world problems effectively.
Visual Representation of Square Roots
Visualizing the square root of a number helps in understanding its value and properties. For the square root of 225, which is 15, we can use geometric shapes and mathematical representations.
Geometric Representation
One way to represent the square root of 225 is by using a square. A square with an area of 225 square units will have sides of length 15 units because \( \sqrt{225} = 15 \).

|
The square above shows that each side is 15 units long, confirming that \( 15 \times 15 = 225 \). |
Number Line Representation
Another way to visualize the square root of 225 is on a number line. By marking the number 15 on the number line, we illustrate the value of \( \sqrt{225} \).

|
The point marked at 15 on the number line represents \( \sqrt{225} \), showing its position relative to other integers. |
Algebraic Representation
We can also represent the square root of 225 using algebraic notation:
\[
\sqrt{225} = 15
\]
This notation is useful in various mathematical contexts and shows that 15 is the number which, when squared, gives 225.
Prime Factorization Representation
The prime factorization of 225 can be used to verify its square root:
\[
225 = 3^2 \times 5^2
\]
\[
\sqrt{225} = \sqrt{3^2 \times 5^2} = 3 \times 5 = 15
\]
Visualizing with Repeated Subtraction
Another method is repeated subtraction, which shows the process of finding the square root by successively subtracting odd numbers until zero is reached:
- 225 - 1 = 224
- 224 - 3 = 221
- 221 - 5 = 216
- 216 - 7 = 209
- 209 - 9 = 200
- 200 - 11 = 189
- 189 - 13 = 176
- 176 - 15 = 161
- 161 - 17 = 144
- 144 - 19 = 125
- 125 - 21 = 104
- 104 - 23 = 81
- 81 - 25 = 56
- 56 - 27 = 29
- 29 - 29 = 0
This sequence shows that after 15 steps, we reach zero, indicating that \( \sqrt{225} = 15 \).
These visual methods help in understanding how the square root of 225, which is 15, is derived and represented in different mathematical forms.
Common Misconceptions about Square Roots
Understanding square roots is crucial in mathematics, but several common misconceptions often arise. Here are some key misconceptions and their clarifications:
-
Misconception 1: Square Roots are Always Positive
Many believe that square roots are always positive. While the principal square root is positive, every positive number actually has two square roots: one positive and one negative. For example, the square root of 225 is both \(+15\) and \(-15\) because both \(15 \times 15 = 225\) and \(-15 \times -15 = 225\).
-
Misconception 2: Only Perfect Squares Have Square Roots
It is often thought that only perfect squares (like 225) have square roots. In reality, every positive number has a square root, though the result may be an irrational number for non-perfect squares. For instance, the square root of 2 is approximately 1.41421356 and it is an irrational number.
-
Misconception 3: The Square Root of a Sum Equals the Sum of the Square Roots
This is a common arithmetic error. The square root of a sum is not equal to the sum of the square roots. Mathematically, \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\). For example, \(\sqrt{4 + 9} = \sqrt{13} \approx 3.605\), whereas \(\sqrt{4} + \sqrt{9} = 2 + 3 = 5\).
-
Misconception 4: Square Roots are Difficult to Understand and Calculate
While square roots can seem challenging, they can be simplified with methods such as prime factorization and the long division method. For example, the square root of 225 can be found by recognizing that 225 = \(15 \times 15\), so \(\sqrt{225} = 15\).
-
Misconception 5: Negative Numbers Do Not Have Square Roots
In the real number system, negative numbers do not have real square roots because no real number squared gives a negative result. However, in the complex number system, they do. The square root of -1 is denoted as \(i\), which stands for an imaginary unit.
Understanding these misconceptions can help in developing a clearer and more accurate comprehension of square roots.
Practice Problems and Solutions
Below are several practice problems related to finding square roots, including detailed solutions to help you understand the process.
-
Problem 1: Find the square root of 144.
Solution:
- We know that 144 is a perfect square.
- We can express 144 as \(12^2\).
- Therefore, the square root of 144 is \( \sqrt{144} = 12 \).
-
Problem 2: Find the square root of 225 using the prime factorization method.
Solution:
- Prime factorize 225: \( 225 = 3^2 \times 5^2 \).
- Take the square root of each factor: \( \sqrt{225} = \sqrt{3^2 \times 5^2} = 3 \times 5 \).
- Therefore, the square root of 225 is \( \sqrt{225} = 15 \).
-
Problem 3: Find the square root of 400 using the long division method.
Solution:
- Set up the long division for 400.
- Pair the digits from the right: (4)(00).
- Find the largest number whose square is less than or equal to 4, which is 2.
- Subtract 4 from 4 to get 0, and bring down the next pair (00) to get 00.
- Double the divisor (2) to get 4, then find the largest number x such that \( 4x \times x \leq 00 \), which is 0.
- The quotient is 20, so \( \sqrt{400} = 20 \).
-
Problem 4: Verify if 361 is a perfect square and find its square root.
Solution:
- We can express 361 as \( 19^2 \).
- Therefore, the square root of 361 is \( \sqrt{361} = 19 \).
- Since 19 is an integer, 361 is a perfect square.
-
Problem 5: Calculate the square root of 1024 using the approximation method.
Solution:
- Find two perfect squares between which 1024 lies. We know \( 31^2 = 961 \) and \( 32^2 = 1024 \).
- Since \( 1024 = 32^2 \), the square root of 1024 is \( \sqrt{1024} = 32 \).
Advanced Topics: Square Roots in Algebra
Square roots play a crucial role in various algebraic concepts. Below, we explore some advanced topics related to square roots in algebra.
1. Solving Quadratic Equations
One of the primary applications of square roots in algebra is in solving quadratic equations. A quadratic equation is of the form \(ax^2 + bx + c = 0\). The quadratic formula, which uses square roots, is given by:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
This formula provides the solutions to any quadratic equation, where the term under the square root, \(b^2 - 4ac\), is known as the discriminant. The discriminant determines the nature of the roots:
- If \(b^2 - 4ac > 0\), there are two distinct real roots.
- If \(b^2 - 4ac = 0\), there is one real root (a repeated root).
- If \(b^2 - 4ac < 0\), there are two complex roots.
2. Simplifying Radical Expressions
Square roots are also used to simplify radical expressions. For example, simplifying \(\sqrt{50}\) involves recognizing that 50 can be factored into 25 and 2, and then using the property of square roots that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):
\[ \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \]
3. Operations with Square Roots
Algebraic operations involving square roots follow specific rules. Here are some key points:
- Addition and Subtraction: Only like terms (same radicand) can be combined. For example, \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\).
- Multiplication: Multiply the coefficients and radicands separately. For example, \(\sqrt{2} \times \sqrt{8} = \sqrt{16} = 4\).
- Division: Simplify by rationalizing the denominator if necessary. For example, \(\frac{\sqrt{3}}{\sqrt{2}} = \sqrt{\frac{3}{2}} = \frac{\sqrt{6}}{2}\).
4. Complex Numbers
Square roots are also fundamental in the study of complex numbers. The imaginary unit \(i\) is defined as \(i = \sqrt{-1}\). This leads to the concept of complex numbers of the form \(a + bi\), where \(a\) and \(b\) are real numbers. For example:
\[ \sqrt{-9} = \sqrt{9 \times -1} = \sqrt{9} \times \sqrt{-1} = 3i \]
5. Exponential and Logarithmic Functions
Square roots can be expressed in exponential form. For instance, \(\sqrt{a} = a^{1/2}\). This representation is useful in solving equations involving exponents and logarithms:
\[ a^{x/2} = b \Rightarrow x \log(a) = 2 \log(b) \Rightarrow x = \frac{2 \log(b)}{\log(a)} \]
6. Solving Higher-Degree Polynomials
For higher-degree polynomial equations, square roots might be used in methods such as completing the square or in the context of polynomial identities.
For example, solving \(x^4 - 16 = 0\) involves recognizing that it can be factored as \((x^2 - 4)(x^2 + 4) = 0\), leading to solutions involving square roots:
\[ x^2 - 4 = 0 \Rightarrow x^2 = 4 \Rightarrow x = \pm 2 \]
\[ x^2 + 4 = 0 \Rightarrow x^2 = -4 \Rightarrow x = \pm 2i \]
Understanding these advanced topics in algebra that involve square roots enhances problem-solving skills and deepens comprehension of algebraic structures.
Square Roots in Geometry
The concept of square roots is integral to various geometric principles and applications. Below are detailed examples and explanations of how square roots are used in geometry:
-
Calculating the Side Length of a Square:
If the area of a square is known, the length of one side can be determined using the square root. For example, a square with an area of 225 square units has a side length of \( \sqrt{225} = 15 \) units.
Mathematically, this can be represented as:
\[ \text{Area} = s^2 \]
\[ s = \sqrt{\text{Area}} \]
-
Distance Between Two Points (Pythagorean Theorem):
The square root is essential in the Pythagorean Theorem, which is used to find the distance between two points in a Cartesian plane. If you have a right triangle with legs of length 9 and 12, the hypotenuse can be found as:
\[ c = \sqrt{a^2 + b^2} \]
\[ c = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15 \]
-
Finding the Radius of a Circle:
If the area of a circle is given, the radius can be found using the square root. For a circle with an area of 225π square units, the radius \( r \) can be calculated as:
\[ \text{Area} = \pi r^2 \]
\[ r^2 = \frac{\text{Area}}{\pi} \]
\[ r = \sqrt{\frac{225\pi}{\pi}} = \sqrt{225} = 15 \]
-
Diagonal of a Square:
The diagonal of a square can be found using the side length and the square root. For a square with side length \( s \), the diagonal \( d \) is given by:
\[ d = s\sqrt{2} \]
For a square with side length 15, the diagonal is:
\[ d = 15\sqrt{2} \approx 21.21 \]
-
Volume and Surface Area of a Cube:
Square roots are used to find the side length of a cube when its volume or surface area is known. For a cube with a volume of 3375 cubic units, the side length \( s \) is:
\[ V = s^3 \]
\[ s = \sqrt[3]{V} = \sqrt[3]{3375} = 15 \]
These examples illustrate the vital role of square roots in solving various geometric problems, highlighting their practical applications in calculating distances, areas, and volumes.

Square Roots in Real-Life Scenarios
Square roots play a crucial role in various real-life scenarios. Understanding how to calculate and apply square roots can simplify many problems and enhance comprehension in different fields. Here are some common real-life applications of square roots:
-
Geometry and Area Calculation:
In geometry, the square root is frequently used to determine the side length of a square when its area is known. For example, if the area of a square field is 225 square meters, the side length of the field can be calculated as follows:
\[
\text{Side length} = \sqrt{225} = 15 \text{ meters}
\] -
Construction and Architecture:
Square roots are essential in construction and architecture for calculating dimensions and ensuring structural integrity. For instance, if a construction blueprint indicates a square section with an area of 225 square feet, the side length of this section is:
\[
\text{Side length} = \sqrt{225} = 15 \text{ feet}
\] -
Physics and Engineering:
Square roots are used in physics and engineering to solve various equations involving quadratic relationships. For example, in determining the root mean square (RMS) value of an alternating current (AC), the square root is used to find the effective value of the current.
\[
\text{RMS} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (I_i^2)}
\] -
Finance and Economics:
In finance, the square root is applied in the calculation of the standard deviation, a measure of investment risk. It helps investors understand the volatility of stock prices and other financial metrics.
\[
\text{Standard Deviation} = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n}}
\] -
Data Analysis:
Square roots are used in data analysis to normalize data distributions. When dealing with skewed data, applying a square root transformation can stabilize variance and make the data more normally distributed.
\[
y' = \sqrt{y}
\] -
Sports:
In sports, square roots are used to calculate distances, speeds, and performance metrics. For example, to find the diagonal distance across a square soccer field with side lengths of 15 meters, the calculation is:
\[
\text{Diagonal} = \sqrt{15^2 + 15^2} = \sqrt{450} = 15\sqrt{2} \approx 21.21 \text{ meters}
\]
These examples illustrate how square roots are indispensable tools across various domains, enhancing accuracy and providing valuable insights into solving practical problems.
Conclusion
The square root of 225 is an important concept in mathematics with diverse applications and implications. It helps in understanding fundamental principles, solving complex problems, and demonstrating the properties of numbers. Calculating the square root of 225, which is 15, showcases the elegance of mathematical operations and their practical uses in various fields such as geometry, algebra, and real-life scenarios.
Throughout this guide, we have explored multiple methods of calculating the square root, delved into its mathematical significance, and discussed how it is applied in both theoretical and practical contexts. The exploration of square roots not only strengthens our numerical skills but also enhances our problem-solving abilities, making it a vital component of mathematical education.
By mastering the concept of square roots, including the square root of 225, students and enthusiasts alike can build a solid foundation for further studies in mathematics and its applications in science, engineering, and everyday life. Understanding square roots paves the way for more advanced topics and fosters a deeper appreciation for the beauty and utility of mathematics.
Tìm căn bậc hai của 225, 256, 20, và căn bậc hai của 40 mà không dùng máy tính
READ MORE:
Hướng dẫn cách tìm căn bậc hai của 225 bằng phương pháp phân tích số nguyên tố. Tìm hiểu cách tính căn bậc hai của 225 một cách dễ dàng và chính xác.
Làm Thế Nào Để Tìm Căn Bậc Hai Của 225 Bằng Phân Tích Số Nguyên Tố / Căn Bậc Hai Của 225 / Căn Bậc Hai 225