Topic - square root of 25: The square root of 25 is more than just a basic math concept; it is a gateway to understanding various mathematical principles and real-world applications. This article delves into the definition, properties, and methods of calculating the square root of 25, highlighting its significance in algebra, geometry, and beyond.
Table of Content
- Understanding the Square Root of 25
- Introduction to Square Roots
- Definition and Concept of Square Roots
- Understanding the Square Root of 25
- Properties of the Square Root of 25
- Mathematical Representation
- Positive and Negative Roots
- Perfect Squares
- Rational and Irrational Numbers
- Methods to Calculate Square Roots
- Prime Factorization Method
- Exponentiation Method
- Using a Calculator
- Applications of Square Roots
- Solving Quadratic Equations
- Geometry Applications
- Physics and Engineering
- Real-world Examples
- Common Mistakes and Misconceptions
- YOUTUBE: Video này giải thích cách tính căn bậc hai của 25, giúp người xem hiểu rõ khái niệm này.
Understanding the Square Root of 25
The square root of 25 is a fundamental concept in mathematics, often encountered in various fields such as algebra, geometry, and real-world applications.
Definition
The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). In other words, it is a value that, when multiplied by itself, gives the original number.
Square Root of 25
For the number 25, the square root can be expressed as follows:
\[\sqrt{25} = 5\]
This is because:
\[5 \times 5 = 25\]
Properties
- Positive and Negative Roots: Although the principal square root of 25 is 5, the number -5 is also a square root of 25 because \((-5) \times (-5) = 25\).
- Perfect Square: The number 25 is a perfect square, meaning it is the square of an integer.
- Rational Number: The square root of 25 is a rational number, as it can be expressed as the fraction \(\frac{5}{1}\).
Calculation Methods
There are several ways to calculate the square root of 25:
- Prime Factorization: Factor 25 into prime factors (5 × 5) and then take the square root of each factor.
- Using Exponents: Express 25 as \(5^2\) and apply the rule \(\sqrt{a^2} = a\).
- Calculator: Use a calculator to find the square root directly.
Applications
Understanding the square root of 25 is useful in various scenarios, such as:
- Solving quadratic equations.
- Geometry, particularly in finding the lengths of sides of squares and right triangles.
- Physics, in calculations involving areas and volumes.
| Mathematical Expression | \(\sqrt{25} = 5\) |
| Verification | \(5 \times 5 = 25\) |
| Negative Root | \(\sqrt{25} = -5\) |
By understanding and utilizing the properties and methods of calculating square roots, one can solve many mathematical problems efficiently.

READ MORE:
Introduction to Square Roots
The concept of a square root is fundamental in mathematics, providing the basis for understanding many advanced topics. The square root of a number is a value that, when multiplied by itself, yields the original number. This relationship can be expressed algebraically as follows: if \( a \) is the square root of \( n \), then \( a^2 = n \). The symbol used to denote the square root is \( \sqrt{} \).
For example, the square root of 25 is denoted as \( \sqrt{25} \), which equals 5 because \( 5 \times 5 = 25 \). Interestingly, both 5 and -5 are square roots of 25, since \( (-5) \times (-5) = 25 \) as well. However, the principal square root, represented by the symbol \( \sqrt{} \), always refers to the non-negative root.
Square roots are not limited to whole numbers. They can also be fractions and irrational numbers. For instance, the square root of 2 (approximately 1.414) cannot be expressed as a simple fraction, making it an irrational number.
To further illustrate, consider the following table of perfect squares and their roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Calculating square roots can be done through various methods such as prime factorization, the repeated subtraction method, and using calculators. Each method has its own application depending on the nature of the number in question—whether it is a perfect square or not.
Understanding square roots is essential as it forms the groundwork for more complex mathematical concepts such as quadratic equations, geometry, and various real-world applications in physics and engineering.
Definition and Concept of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. This concept is fundamental in mathematics and has applications in various fields, including algebra, geometry, and real-world problem solving.
In mathematical terms, if \( x \) is the square root of \( y \), then it is represented as:
\[ x = \sqrt{y} \]
or equivalently:
\[ x^2 = y \]
Here, the symbol '√' is known as the radical symbol, and the number under the radical sign is called the radicand.
Example
For instance, the square of 3 is 9, which means:
\[ 3^2 = 9 \]
Therefore, the square root of 9 is:
\[ \sqrt{9} = 3 \]
Properties of Square Roots
- The square root of a positive number is always positive.
- Every positive number has two square roots: one positive and one negative (e.g., \( \sqrt{25} = 5 \) and \( -\sqrt{25} = -5 \)).
- The square root of zero is zero.
- The square root of a negative number is not a real number (it involves imaginary numbers).
Symbol and Notation
The radical symbol (√) is used to denote the square root. For example, the square root of 16 is written as:
\[ \sqrt{16} = 4 \]
Here, 16 is the radicand.
Mathematical Representation
The function \( f(x) = \sqrt{x} \) represents the square root function. For any non-negative number \( x \), this function gives the principal (non-negative) square root of \( x \).
Square Roots of Perfect Squares
A perfect square is an integer that is the square of another integer. For example, 1, 4, 9, 16, and 25 are perfect squares. Their square roots are integers: 1, 2, 3, 4, and 5, respectively.
Negative Square Roots and Complex Numbers
The square root of a negative number involves imaginary numbers. For example, the square root of -1 is represented as \( i \), where:
\[ i^2 = -1 \]
Thus, the square root of -25 is \( 5i \).
Understanding the Square Root of 25
The square root of 25 is a fundamental concept in mathematics. It is the value that, when multiplied by itself, equals 25. The square root of 25 can be represented using the radical symbol as √25 or in exponential form as 251/2.
Mathematically, the square root of 25 is:
√25 = 5 or √25 = -5
This indicates that both 5 and -5 are square roots of 25 because:
5 × 5 = 25 and (-5) × (-5) = 25
However, when we refer to the square root of a number, we typically mean the principal (positive) square root. Thus, the principal square root of 25 is 5.
Properties of the Square Root of 25
- Principal Square Root: The principal square root of 25 is 5.
- Negative Square Root: The negative square root of 25 is -5.
- Perfect Square: 25 is a perfect square because it is the product of an integer (5) multiplied by itself.
Mathematical Representation
The square root of 25 can be represented in different ways:
- Radical form:
√25 - Exponential form:
251/2or250.5
Positive and Negative Roots
Both positive and negative roots are solutions to the equation x2 = 25:
x2 = 25 implies that x = ±√25, which means x = 5 or x = -5.
Calculation Methods
There are several methods to find the square root of 25:
- Prime Factorization Method:
Prime factorize 25:
25 = 5 × 5Thus,
√25 = √(5 × 5) = 5 - Repeated Subtraction Method:
Subtract consecutive odd numbers from 25 until you reach zero:
- 25 - 1 = 24
- 24 - 3 = 21
- 21 - 5 = 16
- 16 - 7 = 9
- 9 - 9 = 0
The square root of 25 is 5 because it took 5 subtractions.
- Using a Calculator:
Most calculators have a square root function, allowing you to quickly find that
√25 = 5.
In conclusion, understanding the square root of 25 involves recognizing it as both 5 and -5, with practical methods to calculate it, and recognizing its properties and mathematical representations.
Properties of the Square Root of 25
The square root of 25 has several important properties that are useful in various mathematical and real-world applications. These properties are:
- Value: The square root of 25 is 5. This is because \(5 \times 5 = 25\).
- Principal Square Root: The principal (or positive) square root of 25 is denoted as \(\sqrt{25}\) and equals 5.
- Negative Square Root: The negative square root of 25 is \(-\sqrt{25}\), which equals -5.
- Perfect Square: 25 is a perfect square because it is the product of an integer (5) multiplied by itself.
- Rational Number: Both the positive and negative square roots of 25 are rational numbers, as they can be expressed as the fraction \(\frac{5}{1}\) and \(\frac{-5}{1}\) respectively.
- Multiplicative Property: The square root of a product of numbers is the product of their square roots, i.e., \(\sqrt{25 \cdot 1} = \sqrt{25} \cdot \sqrt{1} = 5 \cdot 1 = 5\).
- Non-negative Property: The principal square root of any non-negative number is non-negative. Hence, \(\sqrt{25} = 5\) is non-negative.
These properties illustrate the fundamental nature of the square root of 25 and its role in mathematical operations and real-world applications.

Mathematical Representation
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is represented mathematically as:
\(\sqrt{25} = 5\)
This can be written in various forms:
- Square root notation: \(\sqrt{25} = 5\)
- Exponentiation notation: \(25^{\frac{1}{2}} = 5\)
In general, the square root of a number \(x\) is denoted by \(\sqrt{x}\), where \(\sqrt{x}\) is the non-negative value that satisfies the equation:
\(y^2 = x\)
For example:
- \(\sqrt{9} = 3\) because \(3^2 = 9\)
- \(\sqrt{16} = 4\) because \(4^2 = 16\)
Each positive number has two square roots: one positive and one negative. For the number 25, these roots are +5 and -5, because:
\((+5)^2 = 25\) and \((-5)^2 = 25\)
This can be concisely written using the ± notation:
\(\pm \sqrt{25} = \pm 5\)
However, when we refer to the square root symbol \(\sqrt{}\), it typically means the principal (non-negative) square root. Therefore, \(\sqrt{25}\) is 5.
Table of Square Roots
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Additionally, the square root function \(f(x) = \sqrt{x}\) has important properties:
- Domain: \([0, \infty)\)
- Range: \([0, \infty)\)
- It is an increasing function throughout its domain.
The square root function is widely used in various fields of mathematics, physics, engineering, and many real-world applications.
Positive and Negative Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For any positive number, there are always two square roots: one positive and one negative.
In the case of 25, the square roots are:
+5 -5
Understanding Positive and Negative Roots
When we say the square root of 25 is 5, we are referring to the principal or positive square root, denoted as
This can be illustrated as follows:
\(5 \times 5 = 25\)
\((-5) \times (-5) = 25\)
Mathematical Notation
Mathematically, we express the square roots of 25 as:
Taking the square root of both sides:
Thus,
Principal vs. Negative Root
The principal square root is the non-negative root of a number. When solving equations, the symbol
Application in Quadratic Equations
When solving quadratic equations, it's crucial to consider both roots. For instance:
Consider the equation
Solving for
\(x^2 = 25\)
\(x = \pm \sqrt{25}\)
\(x = \pm 5\)
This yields two solutions:
Summary
In summary, the square root of a number includes both a positive and a negative value. For 25, these roots are +5 and -5, reflecting the property that both
Perfect Squares
A perfect square is a number that can be expressed as the product of an integer with itself. This means that the number has a whole number as its square root. For example, the number 25 is a perfect square because it can be written as \( 5 \times 5 \).
Here is a list of the first few perfect squares:
- 1 (\(1^2 = 1 \))
- 4 (\(2^2 = 4 \))
- 9 (\(3^2 = 9 \))
- 16 (\(4^2 = 16 \))
- 25 (\(5^2 = 25 \))
- 36 (\(6^2 = 36 \))
- 49 (\(7^2 = 49 \))
- 64 (\(8^2 = 64 \))
- 81 (\(9^2 = 81 \))
- 100 (\(10^2 = 100 \))
There are some characteristics that can help identify perfect squares:
- The units place digit of a perfect square is always 0, 1, 4, 5, 6, or 9. For example, 25 ends in 5, and 36 ends in 6.
- If a number ends in 2, 3, 7, or 8, it cannot be a perfect square.
- All perfect squares are non-negative.
Another way to verify if a number is a perfect square is to find its square root:
- If the square root of a number is an integer, the number is a perfect square.
- If the square root is a decimal or fraction, then the number is not a perfect square.
For example, the square root of 49 is 7, an integer, so 49 is a perfect square. However, the square root of 20 is approximately 4.47, which is not an integer, so 20 is not a perfect square.
Perfect squares have practical applications in geometry, algebra, and various real-world contexts where symmetrical properties or area calculations are involved.
Rational and Irrational Numbers
In mathematics, numbers are classified into two main categories: rational and irrational numbers. Understanding these classifications helps in grasping the nature of different types of numbers, including their properties and how they are used.
Rational Numbers
Rational numbers are numbers that can be expressed as the quotient or fraction of two integers, where the numerator is an integer and the denominator is a non-zero integer. The decimal representation of rational numbers either terminates or repeats.
- Examples of rational numbers include:
- Whole numbers: \( 0, 1, 2, 3, \ldots \)
- Integers: \( -3, -2, -1, 0, 1, 2, 3, \ldots \)
- Fractions: \( \frac{1}{2}, \frac{-5}{3}, \frac{22}{7} \)
- Terminating decimals: \( 0.25, 1.75 \)
- Repeating decimals: \( 0.333\ldots (or \ 0.\overline{3}), 2.142142\ldots (or \ 2.\overline{142}) \)
Irrational Numbers
Irrational numbers cannot be expressed as a fraction of two integers. Their decimal representation is non-terminating and non-repeating.
- Examples of irrational numbers include:
- Non-repeating, non-terminating decimals: \( \pi (3.14159265\ldots) \), \( e (2.7182818\ldots) \)
- Square roots of non-perfect squares: \( \sqrt{2}, \sqrt{3}, \sqrt{5} \)
Key Differences
| Aspect | Rational Numbers | Irrational Numbers |
|---|---|---|
| Definition | Can be expressed as the fraction of two integers | Cannot be expressed as the fraction of two integers |
| Decimal Representation | Terminating or repeating | Non-terminating and non-repeating |
| Examples | \( \frac{3}{4}, 0.75, 1.333\ldots \) | \( \pi, \sqrt{2}, 1.414213\ldots \) |
In summary, rational numbers are numbers that can be expressed as a ratio of two integers, with decimal expansions that either terminate or repeat. Irrational numbers, on the other hand, cannot be expressed as a ratio of two integers and have decimal expansions that neither terminate nor repeat. Both rational and irrational numbers together form the set of real numbers, encompassing all possible numerical values.
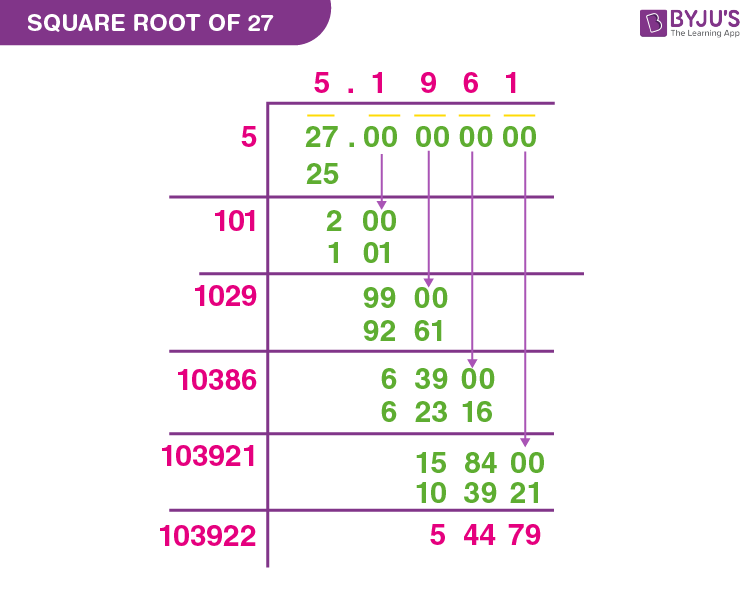
Methods to Calculate Square Roots
Calculating the square root of a number can be approached using several methods. Below, we explore three primary methods for finding square roots: Prime Factorization, Long Division, and Estimation and Refinement.
Prime Factorization Method
This method involves breaking down a number into its prime factors and then pairing these factors to find the square root.
- Find the prime factors of the number.
- Group the prime factors into pairs of identical factors.
- Take one factor from each pair and multiply them to get the square root.
Example: To find the square root of 36:
\[
36 = 2 \times 2 \times 3 \times 3 \\
\sqrt{36} = 2 \times 3 = 6
\]
Long Division Method
The long division method is a systematic approach for finding square roots, especially useful for non-perfect squares.
- Write the number in pairs of digits from right to left.
- Find the largest number whose square is less than or equal to the first pair.
- Subtract the square of this number from the first pair and bring down the next pair.
- Continue the process by finding the next digit of the quotient that fits.
Example: To find the square root of 144:
\[
144 \rightarrow (14)(44) \\
12 \times 12 = 144 \\
\sqrt{144} = 12
\]
Estimation and Refinement
This method involves estimating the square root and then refining the estimate through iteration.
- Estimate a value close to the square root.
- Divide the original number by the estimate to get a quotient.
- Average the estimate and the quotient for a better approximation.
- Repeat the process to improve accuracy.
Example: To find the square root of 50:
\[
\text{Estimate: } 7 \\
\text{Quotient: } \frac{50}{7} \approx 7.14 \\
\text{Average: } \frac{7 + 7.14}{2} = 7.07
\]
Thus, a refined estimate for \(\sqrt{50}\) is approximately 7.07.
These methods provide a foundation for understanding how to calculate square roots, whether for perfect squares or more complex numbers.
Prime Factorization Method
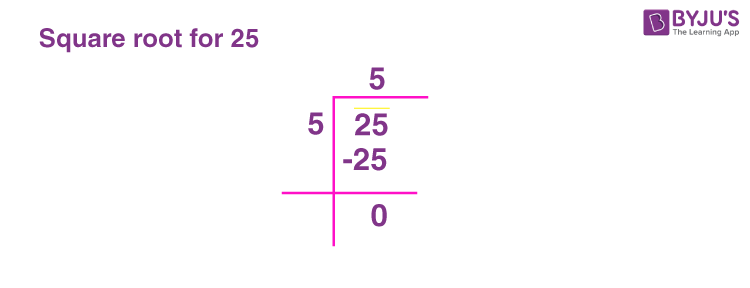
The prime factorization method is a way to find the square root of a number by expressing it as a product of its prime factors. This method is especially useful for perfect squares, which are numbers that have integer square roots. Here are the detailed steps to find the square root of 25 using the prime factorization method:
- Find the prime factors of 25:
Start by dividing 25 by the smallest prime number (2). Since 25 is odd, it is not divisible by 2. The next smallest prime number is 3. Similarly, 25 is not divisible by 3. The next prime number is 5, and 25 is divisible by 5.
Perform the division:
\( 25 \div 5 = 5 \)
Since 5 is also a prime number, we stop here. So, the prime factorization of 25 is:
\( 25 = 5 \times 5 \) or \( 25 = 5^2 \)
- Group the prime factors into pairs:
Since 25 can be expressed as \( 5^2 \), we have a pair of the prime factor 5.
- Take one factor from each pair:
For every pair of prime factors, take one factor. In this case, we have one pair of 5, so we take one 5.
- Multiply the factors taken:
Since there is only one factor (5), the product is simply 5.
- Conclusion:
Therefore, the square root of 25 is:
\( \sqrt{25} = 5 \)
In summary, by expressing 25 as a product of its prime factors \( 25 = 5^2 \) and grouping them into pairs, we determine that the square root of 25 is 5.
Exponentiation Method
The exponentiation method is another effective way to calculate the square root of a number. This method leverages the properties of exponents and powers. Here are the detailed steps to find the square root of 25 using the exponentiation method:
- Understand the relationship between square roots and exponents:
The square root of a number can be represented as that number raised to the power of 1/2. In general, for any positive number \( x \), the square root of \( x \) is given by:
\( \sqrt{x} = x^{1/2} \)
- Express 25 using exponentiation:
To find the square root of 25, we express it as:
\( 25^{1/2} \)
- Calculate the exponentiation:
Recognize that 25 can be written as \( 5^2 \). Thus, we can rewrite the expression as:
\( (5^2)^{1/2} \)
- Apply the power rule:
Use the power rule of exponents, which states that \( (a^m)^n = a^{m \cdot n} \). Applying this rule, we get:
\( (5^2)^{1/2} = 5^{2 \cdot 1/2} = 5^1 \)
Since any number raised to the power of 1 is the number itself, we have:
\( 5^1 = 5 \)
- Conclusion:
Therefore, the square root of 25 using the exponentiation method is:
\( \sqrt{25} = 25^{1/2} = 5 \)
In summary, by expressing the square root of 25 as \( 25^{1/2} \) and applying the properties of exponents, we determine that the square root of 25 is 5.
Using a Calculator
Calculating the square root of a number using a calculator is a quick and accurate method. Here are the detailed steps to find the square root of 25 using a calculator:
- Turn on the calculator:
Ensure that your calculator is turned on and ready for use. Most modern calculators have a dedicated square root button.
- Locate the square root button:
Find the square root button on your calculator. It is usually denoted by the symbol \( \sqrt{} \) or labeled as "sqrt".
- Enter the number 25:
Input the number 25 on your calculator. This can usually be done by pressing the numeric keys.
- Press the square root button:
After entering the number 25, press the square root button \( \sqrt{} \). The calculator will perform the calculation.
- Read the result:
The display will show the result of the calculation. For the square root of 25, the result should be:
\( \sqrt{25} = 5 \)
- Verify the result (optional):
For accuracy, you can verify the result by squaring it. Multiply 5 by 5 to check if the result is 25:
\( 5 \times 5 = 25 \)
This confirms that the square root calculation is correct.
In summary, using a calculator to find the square root of 25 is straightforward: input the number, press the square root button, and read the result, which is 5.

Applications of Square Roots
Square roots have a wide range of applications in various fields such as mathematics, physics, engineering, and everyday life. Understanding these applications can help you appreciate the importance of square roots and how they facilitate problem-solving in different scenarios.
1. Geometry and Trigonometry
In geometry, square roots are essential for calculating distances and lengths. For example, the Pythagorean theorem, which is fundamental in geometry, uses square roots to determine the length of the hypotenuse of a right triangle:
\[
c = \sqrt{a^2 + b^2}
\]
This theorem helps in various real-world applications such as construction, navigation, and computer graphics.
2. Quadratic Equations
Square roots are integral to solving quadratic equations using the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
This formula is widely used in physics, engineering, and economics to model and solve problems involving parabolic paths, optimization, and financial calculations.
3. Physics and Engineering
In physics, square roots are used to calculate various quantities, such as velocity, acceleration, and force. For example, the formula for the period of a pendulum involves a square root:
\[
T = 2\pi \sqrt{\frac{L}{g}}
\]
where \(T\) is the period, \(L\) is the length of the pendulum, and \(g\) is the acceleration due to gravity. Engineers use square roots in structural analysis, signal processing, and electrical circuit design.
4. Statistics and Probability
Square roots are crucial in statistics for calculating standard deviations, which measure the dispersion of a data set. The standard deviation is given by:
\[
\sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}}
\]
where \(\sigma\) is the standard deviation, \(x_i\) represents each data point, \(\mu\) is the mean, and \(N\) is the number of data points. This measure helps in understanding the variability in data and is used in quality control, finance, and research.
5. Real-World Applications
Square roots are used in various practical applications, such as calculating the distance between two points in navigation and mapping, determining the intensity of earthquakes using the Richter scale, and analyzing sound waves in acoustics. For instance, the distance formula in a 2D plane is:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
and in 3D space:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\]
6. Financial Calculations
In finance, square roots are used to calculate compound interest and in risk assessment models. For example, the volatility of a stock is often represented by the standard deviation of its returns, which involves calculating square roots.
7. Computer Science and Algorithms
Square roots are also significant in computer science, particularly in algorithms for searching and optimization. For example, the square root decomposition technique is used in range query problems to improve the efficiency of algorithms.
Overall, the understanding and application of square roots extend across numerous fields, demonstrating their importance in both theoretical and practical aspects of problem-solving.
Solving Quadratic Equations
Quadratic equations are polynomial equations of the form \(ax^2 + bx + c = 0\), where \(a \neq 0\). These equations can have up to two real roots, which can be found using various methods. Below are detailed steps for solving quadratic equations using different methods:
1. Factorization Method
Factorization involves expressing the quadratic equation as a product of its factors. Consider the quadratic equation \(ax^2 + bx + c = 0\).
- Rewrite the middle term \(bx\) as a sum of two terms whose product is \(a \cdot c\).
- Factor the quadratic expression by grouping.
- Set each factor equal to zero and solve for \(x\).
Example:
Solve \(x^2 + 5x + 6 = 0\)
- Rewrite: \(x^2 + 2x + 3x + 6 = 0\)
- Group: \(x(x + 2) + 3(x + 2) = 0\)
- Factor: \((x + 2)(x + 3) = 0\)
- Solutions: \(x = -2\) and \(x = -3\)
2. Completing the Square
This method involves rewriting the quadratic equation in the form of a perfect square trinomial.
- Move the constant term to the other side of the equation: \(ax^2 + bx = -c\).
- Divide all terms by \(a\) (if \(a \neq 1\)).
- Add \(\left(\frac{b}{2a}\right)^2\) to both sides to form a perfect square trinomial on the left side.
- Rewrite the left side as a square: \((x + \frac{b}{2a})^2\).
- Solve for \(x\) by taking the square root of both sides and then isolating \(x\).
Example:
Solve \(x^2 + 4x + 1 = 0\)
- Rewrite: \(x^2 + 4x = -1\)
- Add: \(x^2 + 4x + 4 = 3\) (since \(\left(\frac{4}{2}\right)^2 = 4\))
- Rewrite: \((x + 2)^2 = 3\)
- Solutions: \(x = -2 \pm \sqrt{3}\)
3. Quadratic Formula
The quadratic formula provides a direct way to find the roots of any quadratic equation. The formula is given by:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Steps to use the quadratic formula:
- Identify coefficients \(a\), \(b\), and \(c\) from the quadratic equation \(ax^2 + bx + c = 0\).
- Substitute \(a\), \(b\), and \(c\) into the quadratic formula.
- Calculate the discriminant \(\Delta = b^2 - 4ac\).
- Evaluate the expression to find the roots.
Example:
Solve \(2x^2 + 4x - 6 = 0\)
- Coefficients: \(a = 2\), \(b = 4\), \(c = -6\)
- Discriminant: \(\Delta = 4^2 - 4(2)(-6) = 16 + 48 = 64\)
- Roots: \(x = \frac{-4 \pm \sqrt{64}}{4} = \frac{-4 \pm 8}{4}\)
- Solutions: \(x = 1\) and \(x = -3\)
4. Graphing Method
The graphing method involves plotting the quadratic equation \(y = ax^2 + bx + c\) and finding the points where the graph intersects the x-axis.
- Rewrite the equation as \(y = ax^2 + bx + c\).
- Plot the graph of the quadratic function.
- The x-coordinates of the points where the graph intersects the x-axis are the roots of the quadratic equation.
Example:
Graph the equation \(x^2 - 2x - 3 = 0\). The graph intersects the x-axis at \(x = -1\) and \(x = 3\), which are the roots.
Geometry Applications
Square roots are fundamental in various geometry applications, enabling the calculation of distances, areas, and other important measurements. Here are some key applications of square roots in geometry:
Pythagorean Theorem
The Pythagorean Theorem is one of the most famous applications of square roots. It states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides:
\[c = \sqrt{a^2 + b^2}\]
Where \(c\) is the length of the hypotenuse, and \(a\) and \(b\) are the lengths of the other two sides. For example, if \(a = 3\) and \(b = 4\), then:
\[c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\]
Distance Between Two Points
The distance formula, derived from the Pythagorean Theorem, is used to calculate the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a 2-dimensional plane:
\[D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]
For instance, to find the distance between points \((1, 3)\) and \((4, 7)\):
\[D = \sqrt{(4 - 1)^2 + (7 - 3)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\]
Area of a Square
The area \(A\) of a square with side length \(s\) is given by:
\[A = s^2\]
To find the side length \(s\) from a given area \(A\), you can use the square root:
\[s = \sqrt{A}\]
For example, if the area of a square is 36 square units, the side length is:
\[s = \sqrt{36} = 6\]
Special Triangles
Certain special triangles, such as the 45-45-90 and 30-60-90 triangles, involve square roots in their side length ratios. For example:
- A 45-45-90 triangle has sides in the ratio \(1:1:\sqrt{2}\).
- A 30-60-90 triangle has sides in the ratio \(1:\sqrt{3}:2\).
These ratios allow for the calculation of unknown side lengths using square roots when one side length is known.
Circle Geometry
In circle geometry, square roots are used to calculate the radius \(r\) or diameter \(d\) from the area \(A\) of the circle:
\[A = \pi r^2\]
Solving for \(r\) gives:
\[r = \sqrt{\frac{A}{\pi}}\]
For example, if the area of a circle is 50 square units, the radius is:
\[r = \sqrt{\frac{50}{\pi}} \approx 3.99\]
Applications in Coordinate Geometry
Square roots are essential in coordinate geometry for finding the lengths of segments, the equations of circles, and solving other geometric problems in the coordinate plane.
These examples illustrate how square roots are integral to solving various geometric problems, making them a crucial tool in both theoretical and applied mathematics.
Physics and Engineering
The concept of square roots, including the square root of 25, plays a significant role in various fields of physics and engineering. Understanding and utilizing square roots are crucial in solving problems related to measurements, waveforms, and dynamic systems. Here’s a detailed look at how square roots are applied in these disciplines:
1. Kinematics and Dynamics
In physics, the motion of objects is often analyzed using kinematic equations that include square roots. For instance, the time it takes for an object to fall a certain distance under gravity can be calculated using the equation:
\[
t = \sqrt{\frac{2h}{g}}
\]
where t is the time, h is the height, and g is the acceleration due to gravity. Here, solving for t involves taking the square root, illustrating how square roots are fundamental in predicting the behavior of moving objects.
2. Electrical Engineering
In electrical engineering, the root mean square (RMS) value is used to measure the effective voltage or current of an AC (alternating current) signal. The RMS value of a signal is essential because it provides a measure of the equivalent DC (direct current) value that would produce the same power dissipation in a resistor. The RMS value is calculated as follows:
\[
V_{RMS} = \sqrt{\frac{1}{T} \int_0^T v(t)^2 \, dt}
\]
where \( V_{RMS} \) is the RMS voltage, \( T \) is the period of the waveform, and \( v(t) \) is the instantaneous voltage. This calculation involves squaring the signal, averaging over time, and then taking the square root.
3. Structural Engineering
In structural engineering, the strength of materials and the stability of structures often require understanding the square root relationship. For example, the natural frequency of a vibrating system (like a building or a bridge) is given by:
\[
f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\]
where f is the natural frequency, k is the stiffness of the system, and m is the mass. Here, the square root helps determine how quickly the system oscillates under a given load.
4. Signal Processing
In signal processing, the power of a signal is often analyzed using the RMS value, which involves square roots. This is crucial in designing filters and amplifiers in telecommunications. The signal's power in decibels (dB) is calculated using the formula:
\[
P_{dB} = 10 \log_{10} \left( \frac{P}{P_0} \right)
\]
where \( P \) is the power of the signal, and \( P_0 \) is a reference power. Although this formula doesn't directly use square roots, understanding the power often involves RMS values and their square roots.
5. Fluid Dynamics
In fluid dynamics, the behavior of fluids is often analyzed using equations that involve square roots. For example, the flow rate of a fluid through an orifice can be determined using Torricelli’s law:
\[
v = \sqrt{2gh}
\]
where v is the velocity of the fluid, g is the acceleration due to gravity, and h is the height of the fluid above the orifice. This illustrates how square roots help in calculating the speed at which fluids escape from containers.
6. Quantum Mechanics
In quantum mechanics, the wave functions of particles are often described using equations that involve square roots. The normalization of these wave functions ensures that the total probability of finding a particle is one, requiring the integral of the square of the wave function to equal one:
\[
\int_{-\infty}^{\infty} |\psi(x)|^2 \, dx = 1
\]
where \( \psi(x) \) is the wave function of the particle. Solving such problems frequently involves operations with square roots to find probabilities and expectation values.
Conclusion
From analyzing the motion of objects to measuring electrical signals and understanding fluid dynamics, the square root of numbers like 25 is a fundamental concept in physics and engineering. These applications highlight the ubiquitous nature of square roots in solving real-world problems and designing systems across various engineering disciplines.
Real-world Examples
The square root of 25, which is 5, finds its applications in various real-world scenarios. Here are some detailed examples illustrating how this mathematical concept is used:
-
Architecture and Construction:
When designing buildings or structures, architects often use square roots to calculate diagonal lengths. For instance, if a square room has sides of 5 meters, the diagonal across the room can be found using the Pythagorean theorem. Since the sides are both 5 meters, the diagonal (d) is given by:
\[
d = \sqrt{5^2 + 5^2} = \sqrt{25 + 25} = \sqrt{50} = 5\sqrt{2}
\] -
Sports:
In sports like track and field, the square root is used to measure distances. For example, if an athlete needs to run around a square field where each side is 5 meters long, the distance of the diagonal path they would take can be calculated as:
\[
d = \sqrt{5^2 + 5^2} = \sqrt{50} = 5\sqrt{2} \approx 7.07 \text{ meters}
\] -
Gardening and Landscaping:
In gardening, square roots help determine the length of fencing needed for a square garden plot. If each side of the plot is 5 meters, the total length of the fencing required can be calculated using the perimeter formula for a square:
\[
\text{Perimeter} = 4 \times \text{side length} = 4 \times 5 = 20 \text{ meters}
\] -
Technology and Computing:
In computing, algorithms often use square roots for graphics and game development. For instance, calculating the distance between two points (x1, y1) and (x2, y2) on a screen can be done using the distance formula, which involves square roots:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\] -
Physics:
Square roots are used in physics to determine various quantities. For example, the formula for the period (T) of a simple pendulum is:
\[
T = 2\pi\sqrt{\frac{L}{g}}
\]where L is the length of the pendulum and g is the acceleration due to gravity.
These examples highlight how understanding and applying the concept of square roots is essential in solving practical problems across different fields.
Common Mistakes and Misconceptions
Understanding square roots can be challenging, and students often make common mistakes. Here are some frequent errors and misconceptions associated with square roots, along with explanations to help avoid them:
- Incorrect Distribution: One common mistake is assuming that the square root of a sum is the sum of the square roots, i.e., \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\). This is not true. For example, \(\sqrt{25 + 9} \neq \sqrt{25} + \sqrt{9}\); rather, \(\sqrt{34} \neq 5 + 3\).
- Negative Square Roots: Students often forget that the square root of a number is always non-negative in the context of real numbers. For example, while solving \(\sqrt{25}\), the answer is 5, not -5, because square roots are defined to be the principal (positive) roots.
- Product of Square Roots: A common misconception is misinterpreting the property \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\). While this property holds true, students sometimes apply it incorrectly in situations where it does not apply, such as assuming \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\).
- Simplifying Roots Incorrectly: When simplifying expressions involving square roots, students might make mistakes like \(\sqrt{4 \cdot 9} \neq 2 \cdot 3\). The correct simplification should be \(\sqrt{36} = 6\).
- Perfect Squares Misconceptions: Students sometimes forget which numbers are perfect squares. A perfect square is an integer that is the square of another integer, such as \(1, 4, 9, 16, 25, \ldots\).
- Ignoring Complex Roots: For negative radicands, students might mistakenly assume that there are no roots. However, in the context of complex numbers, \(\sqrt{-1} = i\), where \(i\) is the imaginary unit.
To avoid these mistakes, it's crucial to understand the properties of square roots and practice applying them correctly:
| Misconception | Correction |
|---|---|
| \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\) | \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\) |
| \(\sqrt{a \cdot b} \neq \sqrt{a} \cdot \sqrt{b}\) | \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) |
| \(\sqrt{4 \cdot 9} = 2 \cdot 3\) | \(\sqrt{4 \cdot 9} = \sqrt{36} = 6\) |
By recognizing and understanding these common errors, students can improve their skills in working with square roots and avoid these pitfalls in their calculations.
Video này giải thích cách tính căn bậc hai của 25, giúp người xem hiểu rõ khái niệm này.
Căn bậc hai của 25
READ MORE:
Video này giải thích lý do tại sao căn bậc hai của 25 là 5 và tại sao nhiều người có câu trả lời đúng nhưng không hiểu lý do.
Căn bậc hai của 25 bằng bao nhiêu? Nhiều người không hiểu vì sao họ có câu trả lời ĐÚNG!