Topic square root of 2/4: Discover the simplified steps to understand the square root of 2/4 in this comprehensive guide. Learn how to break down fractions, calculate square roots, and avoid common mistakes. This article provides a clear and concise explanation, making it easy for readers of all levels to grasp this mathematical concept.
Table of Content
- Understanding the Square Root of 2/4
- Introduction to Square Roots
- Mathematical Definition of Square Root
- Understanding Fractions
- Step-by-Step Calculation of the Square Root of 2/4
- Properties of Square Roots
- Simplifying Square Roots
- Rationalizing the Denominator
- Common Mistakes and Misconceptions
- Applications of Square Roots in Real Life
- Advanced Topics in Square Roots
- Conclusion
- YOUTUBE: Video giới thiệu về căn bậc hai của 2, giải thích tại sao số này là số vô tỉ và ứng dụng của nó trong toán học và cuộc sống hàng ngày.
Understanding the Square Root of 2/4
The square root of a fraction can be determined by taking the square root of the numerator and the denominator separately. Here, we will find the square root of step by step.
Step-by-Step Calculation
-
First, express the fraction:
-
Next, take the square root of both the numerator and the denominator:
-
Simplify the expression, since the square root of 1 is 1:
Final Answer
The square root of is , which can also be expressed as .

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations that are essential for solving various equations and problems. Understanding square roots involves grasping the concept of finding a number which, when multiplied by itself, gives the original number. For example, the square root of 4 is 2, because 2 × 2 = 4.
Here are some important points about square roots:
- The square root of a positive number has both a positive and a negative value. For instance, the square root of 9 is ±3.
- The square root of 0 is 0.
- There is no real square root of a negative number; instead, these roots are called imaginary numbers.
To find the square root of a fraction, such as , we use the property that the square root of a fraction is the same as the fraction of the square roots:
Let's break down the calculation step by step:
- Identify the numerator and denominator of the fraction: 2 (numerator) and 4 (denominator).
- Calculate the square root of the numerator: .
- Calculate the square root of the denominator: .
- Express the square root of the fraction as a fraction of the square roots: .
Thus, the square root of simplifies to .
Mathematical Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, if , then
Here are some key points about square roots:
- Every positive number has two square roots: a positive root and a negative root. For example, the square roots of 9 are 3 and -3.
- The square root of zero is zero.
- Negative numbers do not have real square roots. Instead, they have imaginary roots.
To find the square root of a fraction, such as , we can use the property that the square root of a fraction is equal to the square root of the numerator divided by the square root of the denominator. Let's illustrate this step by step:
-
Express the fraction in its simplest form:
-
Apply the square root to both the numerator and the denominator separately:
-
Since the square root of 1 is 1, we simplify the expression:
Thus, the square root of simplifies to . This approach highlights the importance of understanding the properties of square roots and how they apply to both whole numbers and fractions.
Understanding Fractions
Fractions represent parts of a whole and are composed of a numerator and a denominator. The numerator, positioned above the fraction line, indicates how many parts are taken, while the denominator, positioned below, signifies the total number of equal parts into which the whole is divided.
Here are some fundamental concepts about fractions:
- Proper Fractions: The numerator is less than the denominator, such as .
- Improper Fractions: The numerator is greater than or equal to the denominator, such as .
- Mixed Numbers: A combination of a whole number and a proper fraction, such as 1.
- Equivalent Fractions: Different fractions that represent the same value, such as and .
To simplify a fraction, divide both the numerator and the denominator by their greatest common divisor (GCD). For example, consider the fraction :
- Identify the GCD of 2 and 4, which is 2.
- Divide both the numerator and the denominator by the GCD:
The simplified form of is . Simplifying fractions is crucial for performing operations like addition, subtraction, multiplication, and division more efficiently.
When dealing with the square root of a fraction, such as , understanding fractions becomes essential. Simplifying the fraction before taking the square root often makes the calculation easier. In this case:
- Simplify to .
- Take the square root of the numerator and the denominator separately:
Understanding and simplifying fractions are foundational skills in mathematics, enabling more complex operations and applications.
Step-by-Step Calculation of the Square Root of 2/4
Calculating the square root of a fraction involves taking the square root of both the numerator and the denominator separately. Here, we will go through the detailed steps to find the square root of .
-
Simplify the fraction:
The given fraction is . To simplify it, find the greatest common divisor (GCD) of 2 and 4, which is 2. Divide both the numerator and the denominator by 2:
So, simplifies to .
-
Express the square root of the simplified fraction:
The next step is to find the square root of . According to the property of square roots of fractions, we can take the square root of the numerator and the denominator separately:
-
Simplify the square roots:
The square root of 1 is 1:
So, the expression simplifies to:
-
Rationalize the denominator (if required):
To rationalize the denominator, multiply both the numerator and the denominator by :
Thus, the rationalized form is:
In summary, the square root of is , which can also be expressed in its rationalized form as .
Properties of Square Roots
Square roots have several important properties that are useful in mathematical calculations and problem-solving. Understanding these properties helps in simplifying expressions and solving equations effectively. Here are some key properties of square roots:
- Non-Negative Property: The square root of a non-negative number is always non-negative. For any non-negative number , is also non-negative.
- Product Property: The square root of a product is equal to the product of the square roots of the factors. For any non-negative numbers and :
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. For any non-negative numbers and (with ≠ 0):
- Power Property: The square root of a number squared is the absolute value of the original number. For any real number :
- Sum and Difference Property: The square root of a sum or difference is not the sum or difference of the square roots. In other words, ≠ and ≠ .
These properties can be applied to simplify and solve various mathematical problems. For example, let's consider the fraction and find its square root:
-
Using the quotient property, we can separate the square root of the fraction:
-
Next, calculate the square root of the numerator and the denominator separately:
-
Combine the results to get the square root of the fraction:
By understanding and applying these properties, solving problems involving square roots becomes more intuitive and manageable.
Simplifying Square Roots
Square roots can often be simplified to make them easier to work with. Simplifying a square root involves factoring out perfect squares from under the radical sign. Here, we'll focus on simplifying the square root of the fraction 2/4.
- Express the fraction as a single square root:
The square root of a fraction can be expressed as the square root of the numerator divided by the square root of the denominator:
\[\sqrt{\frac{2}{4}} = \frac{\sqrt{2}}{\sqrt{4}}\]
- Simplify the denominator:
The square root of 4 is 2 because \(4 = 2^2\):
\[\sqrt{4} = 2\]
So, our expression now looks like this:
\[\frac{\sqrt{2}}{2}\]
- Rationalizing the expression (if necessary):
In some cases, you might want to rationalize the denominator (i.e., make the denominator a rational number). However, in this example, the denominator is already rational, so no further simplification is needed.
Thus, the simplified form of \(\sqrt{\frac{2}{4}}\) is \(\frac{\sqrt{2}}{2}\).
Example Problems
- Example 1: Simplify \(\sqrt{\frac{9}{16}}\)
Solution:
- Express the fraction as a single square root: \(\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}}\)
- Simplify the numerator and the denominator: \(\frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}\)
- Therefore, \(\sqrt{\frac{9}{16}} = \frac{3}{4}\).
- Example 2: Simplify \(\sqrt{\frac{5}{25}}\)
Solution:
- Express the fraction as a single square root: \(\sqrt{\frac{5}{25}} = \frac{\sqrt{5}}{\sqrt{25}}\)
- Simplify the denominator: \(\frac{\sqrt{5}}{\sqrt{25}} = \frac{\sqrt{5}}{5}\)
- Therefore, \(\sqrt{\frac{5}{25}} = \frac{\sqrt{5}}{5}\).
Rationalizing the Denominator
Rationalizing the denominator is a process used to eliminate radicals from the denominator of a fraction. This is done by multiplying both the numerator and the denominator by a suitable conjugate or the radical present in the denominator. Here's a detailed step-by-step guide to rationalizing the denominator, specifically for the fraction :
-
Identify the Radical in the Denominator:
In the given fraction , the denominator is 4, which is a perfect square. The square root of 4 is 2. So, we rewrite the fraction as:
-
Multiply by the Conjugate:
For fractions where the denominator is not a perfect square, we use the conjugate. For example, consider the fraction . The conjugate of is .
-
Multiply the Numerator and Denominator:
Multiply both the numerator and the denominator by this conjugate:
Thus, the rationalized form is .
-
Simplify the Result:
Ensure the fraction is in its simplest form. If there are common factors in the numerator and the denominator, divide them out.
In our earlier example, since is already simplified, we do not need further steps.
By following these steps, you can effectively rationalize the denominator of any fraction containing a radical.
Common Mistakes and Misconceptions
When working with square roots, especially involving fractions like \( \frac{2}{4} \), several common mistakes and misconceptions can occur. Understanding these can help prevent errors and deepen comprehension. Below are some of the frequent mistakes along with clarifications:
- Mistake: Misinterpreting the Numerator and Denominator
One common misconception is misunderstanding the relationship between the numerator and denominator when simplifying square roots of fractions. For example, thinking \( \sqrt{\frac{2}{4}} = \frac{\sqrt{2}}{4} \). The correct simplification is:
\[ \sqrt{\frac{2}{4}} = \sqrt{\frac{1}{2}} \]
- Mistake: Incorrectly Simplifying Square Roots
Another mistake is not fully simplifying the square root of a fraction. For \( \sqrt{\frac{2}{4}} \), instead of stopping at \( \frac{\sqrt{2}}{2} \), recognize that \( \frac{2}{4} = \frac{1}{2} \), thus:
\[ \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
- Misconception: Square Root and Fraction Operation Confusion
Students often confuse the operations involving square roots and fractions. A common error is treating the square root operation as if it distributes over addition or multiplication inside the fraction improperly. For instance, incorrectly simplifying \( \sqrt{\frac{a+b}{c}} \) as \( \frac{\sqrt{a} + \sqrt{b}}{\sqrt{c}} \), which is not correct. The correct simplification follows the rule:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
- Misconception: Negative Values and Square Roots
A frequent error is assuming that the square root of a negative fraction has no real solution. For instance, students might think \( \sqrt{\frac{-4}{16}} \) has no solution. However, for negative values, the square root results in an imaginary number:
\[ \sqrt{\frac{-4}{16}} = \sqrt{\frac{-1}{4}} = \frac{i}{2} \]
- Mistake: Forgetting to Rationalize the Denominator
When the square root of a fraction results in a denominator with a square root, students often forget to rationalize it. For instance, with \( \frac{1}{\sqrt{2}} \), the correct rationalization is:
\[ \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \]
Understanding these common mistakes and misconceptions is crucial in mastering the concepts of square roots and fractions. Taking the time to recognize and correct these errors can significantly improve mathematical accuracy and confidence.
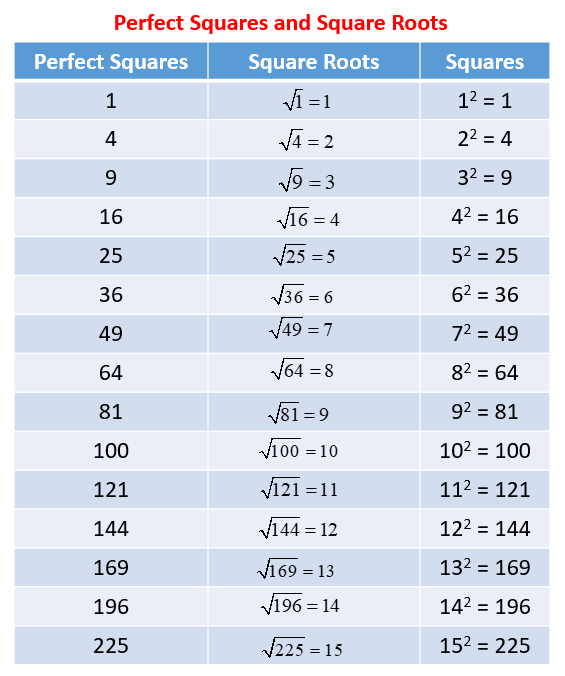
Applications of Square Roots in Real Life
Square roots have numerous applications across various fields and everyday activities. Understanding these applications can enhance our appreciation of the mathematical concept and its practical utility.
- Architecture and Construction:
Designing buildings and bridges often involves calculating square roots to determine correct lengths and angles for structural integrity and aesthetic appeal. For instance, the diagonal of a square room is determined using the square root of the sum of the squares of its sides.
- Science and Engineering:
In physics, square roots are used to calculate various parameters such as force, energy, and velocity. For example, the formula for the period of a pendulum involves the square root of its length divided by the gravitational constant.
- Navigation and Geolocation:
Calculating distances between points on a map frequently uses square roots, especially when applying the Pythagorean theorem to find the shortest path. This is crucial in fields like aviation, maritime navigation, and even hiking.
- Finance and Economics:
Square roots are utilized in determining the volatility of stock prices, represented by the standard deviation. This helps in assessing investment risks and making informed financial decisions.
- Computer Graphics and Digital Imaging:
In computer graphics, calculating distances and rendering images accurately requires the use of square roots to achieve realism and precision, such as in determining pixel distances and angles.
- Sports and Physical Fitness:
Analyzing movements and optimizing performance often involves square root calculations. For example, determining the trajectory of a ball or optimizing an athlete's performance metrics involves using square roots to calculate distances and angles.
These examples illustrate the wide-ranging applications of square roots, demonstrating their importance beyond theoretical mathematics and into practical, real-world scenarios.
Advanced Topics in Square Roots
In advanced mathematics, square roots play a critical role in various complex concepts and applications. Below, we explore several advanced topics related to square roots, providing detailed explanations and step-by-step processes.
1. Irrational Numbers and Square Roots
Many square roots result in irrational numbers, meaning they cannot be expressed as a simple fraction. For example, \( \sqrt{2} \) is irrational. Understanding the properties of irrational numbers is crucial in advanced mathematics.
Key characteristics include:
- Non-repeating, non-terminating decimal expansion.
- Cannot be precisely represented as a ratio of two integers.
2. Complex Numbers and Square Roots
Square roots extend beyond real numbers into the realm of complex numbers. The square root of a negative number involves the imaginary unit \(i\), where \( i = \sqrt{-1} \).
For example:
\[
\sqrt{-4} = \sqrt{4 \cdot (-1)} = 2i
\]
Complex numbers are expressed as \( a + bi \), where \( a \) and \( b \) are real numbers.
3. Solving Quadratic Equations
Square roots are fundamental in solving quadratic equations using the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
The term \( \sqrt{b^2 - 4ac} \) is the discriminant and determines the nature of the roots.
- If the discriminant is positive, there are two distinct real roots.
- If it is zero, there is one real root.
- If it is negative, there are two complex conjugate roots.
4. Differential Equations
Square roots appear in solutions to differential equations, particularly in the context of characteristic equations for linear differential equations with constant coefficients. For example:
The differential equation:
\[
ay'' + by' + cy = 0
\]
leads to the characteristic equation:
\[
ar^2 + br + c = 0
\]
The roots of this quadratic equation can involve square roots, affecting the form of the solution.
5. Eigenvalues and Eigenvectors
In linear algebra, square roots are used in the computation of eigenvalues and eigenvectors. The characteristic polynomial of a matrix often involves solving a quadratic equation, requiring the use of square roots.
For a 2x2 matrix \( A \), the eigenvalues \( \lambda \) are found from:
\[
\det(A - \lambda I) = 0
\]
resulting in a quadratic equation in \( \lambda \) where square roots may be involved.
6. Applications in Geometry and Physics
Square roots are prevalent in geometry, such as in the Pythagorean theorem, where the length of the hypotenuse \( c \) of a right triangle with legs \( a \) and \( b \) is given by:
\[
c = \sqrt{a^2 + b^2}
\]
In physics, square roots appear in formulas for wave speeds, potential energy, and in Schrödinger's equation in quantum mechanics.
Understanding these advanced applications of square roots helps in gaining deeper insights into higher-level mathematics and its applications in various fields.
Conclusion
In conclusion, understanding the square root of involves a blend of basic arithmetic and algebraic concepts. Simplifying this expression, we find that it equals , showcasing how fractions and square roots interact.
Throughout this guide, we explored the fundamental properties of square roots, including their definition, simplification, and rationalization techniques. We also addressed common mistakes and misconceptions that can arise when dealing with square roots, ensuring a clear and accurate understanding of the topic.
The applications of square roots in real life are vast, from engineering and physics to finance and everyday problem-solving. These concepts help us model and solve problems involving quadratic relationships and geometric properties.
Advanced topics in square roots, such as irrational numbers and their proofs, reveal the deeper mathematical structures that govern these numbers. For instance, the square root of 2 is a classic example of an irrational number, highlighting the complexity and beauty of mathematics.
By mastering these concepts, students and enthusiasts can build a solid foundation in mathematics, enabling them to tackle more complex problems and appreciate the elegance of mathematical reasoning.
Overall, the journey through understanding the square root of not only enhances our mathematical skills but also enriches our appreciation for the subject's depth and utility.
Video giới thiệu về căn bậc hai của 2, giải thích tại sao số này là số vô tỉ và ứng dụng của nó trong toán học và cuộc sống hàng ngày.
Căn Bậc Hai của 2
READ MORE:
Video chứng minh rằng căn bậc hai của 2 là số vô tỉ, giải thích chi tiết và dễ hiểu về khái niệm và cách chứng minh.
Chứng Minh Rằng Căn Bậc Hai của Hai Là Số Vô Tỉ