Topic how do you simplify square roots with variables: Understanding how to simplify square roots with variables is essential for mastering algebra. This guide will walk you through the process step-by-step, making it easy to handle even complex expressions. Learn how to break down variables, deal with multiple factors, and apply the fundamental rules of radicals to simplify any square root with confidence.
Table of Content
- How to Simplify Square Roots with Variables
- Introduction to Simplifying Square Roots with Variables
- Understanding Square Roots and Radicals
- Basic Steps for Simplifying Square Roots
- Prime Factorization and Perfect Squares
- Using Exponents in Simplification
- Simplifying Square Roots of Monomials
- Examples of Simplifying Square Roots with Single Variables
- Examples of Simplifying Square Roots with Multiple Variables
- Simplifying Square Roots Involving Fractions
- Quotient Property of Square Roots
- Examples of Simplifying Square Roots of Fractions
- Handling Even and Odd Exponents in Variables
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- Advanced Techniques for Complex Expressions
- Summary and Key Takeaways
- YOUTUBE: Video này hướng dẫn cách đơn giản hoá căn bậc hai với biến số, giúp bạn hiểu rõ hơn về chủ đề này trong toán học.
How to Simplify Square Roots with Variables
Simplifying square roots involving variables requires understanding basic rules of algebra and the properties of square roots:
- Factorization: Express the expression under the square root as a product of perfect squares.
- Isolate the Square Root: Separate the perfect square factors from other terms.
- Apply Square Root Property: Take the square root of the perfect square factors.
- Simplify: Combine like terms if applicable.
For example, to simplify \( \sqrt{18x^4} \):
| Step 1: | \( \sqrt{18x^4} = \sqrt{9 \cdot 2 \cdot x^4} \) |
| Step 2: | \( = \sqrt{9} \cdot \sqrt{2} \cdot \sqrt{x^4} \) |
| Step 3: | \( = 3 \cdot \sqrt{2} \cdot x^2 \) |
| Final Answer: | \( 3x^2\sqrt{2} \) |
Remember to check if there are any restrictions on the variables that could affect simplification. Practicing with different examples will improve proficiency in handling square roots with variables.

READ MORE:
Introduction to Simplifying Square Roots with Variables
In this section, we will explore the techniques for simplifying square roots that include variables. Understanding how to handle variables under a radical is crucial for solving more complex algebraic problems. We will break down the process into manageable steps to ensure clarity and ease of learning.
To simplify square roots with variables, follow these steps:
- Identify and separate the coefficients (numbers) from the variables inside the radical.
- Factor both the coefficients and the variables into their prime factors.
- Pair up identical factors since the square root of a squared term is the term itself.
- Move the pairs outside the radical, leaving any unpaired factors inside.
Let's look at some examples to illustrate these steps:
-
Example 1: Simplify \( \sqrt{18x^4y^2} \)
- Factorize inside the radical: \( \sqrt{2 \cdot 3^2 \cdot x^4 \cdot y^2} \)
- Pair the factors: \( \sqrt{(3^2) \cdot (x^2)^2 \cdot y^2 \cdot 2} \)
- Simplify by taking out pairs: \( 3x^2y\sqrt{2} \)
So, \( \sqrt{18x^4y^2} = 3x^2y\sqrt{2} \)
-
Example 2: Simplify \( \sqrt{50a^3b^6} \)
- Factorize inside the radical: \( \sqrt{2 \cdot 5^2 \cdot a^3 \cdot (b^3)^2} \)
- Pair the factors: \( \sqrt{(5^2) \cdot (b^3)^2 \cdot a^2 \cdot a \cdot 2} \)
- Simplify by taking out pairs: \( 5b^3a\sqrt{2a} \)
So, \( \sqrt{50a^3b^6} = 5b^3a\sqrt{2a} \)
By practicing these steps, you will become proficient in simplifying square roots with variables, allowing you to tackle more advanced algebraic equations with confidence.
Understanding Square Roots and Radicals
The concept of square roots and radicals is fundamental in algebra and higher-level mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. Similarly, radicals extend this concept to roots beyond the square root, such as cube roots.
Let's break down the key points to understand square roots and radicals:
-
Square Roots:
The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). This is denoted as \(\sqrt{x}\). For example, \(\sqrt{9} = 3\) because \(3^2 = 9\).
-
Radical Expressions:
A radical expression includes a root symbol (√). The number or expression inside the root symbol is called the radicand. For example, in \(\sqrt{16}\), 16 is the radicand.
-
Properties of Radicals:
- \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \(\sqrt{a^2} = |a|\)
-
Examples:
Consider the expression \(\sqrt{9x^6}\). This can be simplified by recognizing that \(9 = 3^2\) and \(x^6 = (x^3)^2\), thus:
\[\sqrt{9x^6} = \sqrt{(3^2)(x^3)^2} = 3|x^3|\]
-
Simplifying Radicals with Variables:
When simplifying radicals that include variables, look for perfect square factors. For example, in \(\sqrt{100x^2y^4}\), we can factor as follows:
\[\sqrt{100x^2y^4} = \sqrt{10^2x^2(y^2)^2} = 10|x|y^2\]
Understanding these basics allows for simplifying more complex expressions and solving algebraic equations involving radicals effectively.
Basic Steps for Simplifying Square Roots
Simplifying square roots involves a few systematic steps to ensure that the expression is reduced to its simplest form. Here is a detailed guide to help you through the process:
- Identify Perfect Squares:
Look for perfect square factors within the radicand (the number under the square root sign). Perfect squares are numbers like 1, 4, 9, 16, 25, and so on.
- Prime Factorization:
Break down the radicand into its prime factors. For example, if you have \(\sqrt{72}\), you can express 72 as \(2^3 \times 3^2\).
- Separate the Factors:
Express the square root of the product as the product of square roots. For instance, \(\sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2^3} \times \sqrt{3^2}\).
- Simplify the Square Roots:
Extract the square roots of the perfect squares. In the example, \(\sqrt{2^3} \times \sqrt{3^2}\), we get \(2 \sqrt{2} \times 3 = 6 \sqrt{2}\).
- Combine and Simplify:
Multiply the simplified terms together to get the final simplified form. Using the example, the simplified form of \(\sqrt{72}\) is \(6 \sqrt{2}\).
By following these steps, you can simplify any square root, making complex expressions more manageable.
Prime Factorization and Perfect Squares
Prime factorization and recognizing perfect squares are essential techniques for simplifying square roots, especially when variables are involved. Here's a detailed, step-by-step guide on how to apply these methods effectively.
-
Prime Factorization:
Break down the number inside the square root into its prime factors. For example, to simplify
\(\sqrt{72}\), we start with the prime factorization of 72:- \(72 = 2 \times 36\)
- \(36 = 2 \times 18\)
- \(18 = 2 \times 9\)
- \(9 = 3 \times 3\)
Thus, \(72 = 2 \times 2 \times 2 \times 3 \times 3\) or \(72 = 2^3 \times 3^2\).
-
Identifying Perfect Squares:
Group the prime factors into pairs of identical numbers, as these will form perfect squares.
- \(\sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2^2 \times 2 \times 3^2}\)
Recognize that \(2^2\) and \(3^2\) are perfect squares.
-
Extracting Perfect Squares:
Take the square root of each perfect square factor and place it outside the radical:
- \(\sqrt{2^2} = 2\)
- \(\sqrt{3^2} = 3\)
So, \(\sqrt{72} = \sqrt{2^2 \times 3^2 \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
-
Simplifying Variables:
Apply the same process to variables. For instance, to simplify \(\sqrt{50x^4y^2}\):
- \(50 = 2 \times 5^2\)
- \(\sqrt{50x^4y^2} = \sqrt{2 \times 5^2 \times x^4 \times y^2}\)
Since \(5^2\), \(x^4\), and \(y^2\) are perfect squares, extract them:
- \(\sqrt{5^2} = 5\)
- \(\sqrt{x^4} = x^2\)
- \(\sqrt{y^2} = y\)
So, \(\sqrt{50x^4y^2} = 5x^2y\sqrt{2}\).
Using these steps, you can simplify any square root with variables by breaking down the expression into its prime factors and extracting the perfect squares.

Using Exponents in Simplification
When simplifying square roots with variables, exponents play a crucial role. Understanding how to handle exponents can make the process much easier. Here are the detailed steps to simplify square roots using exponents:
-
Identify the Variables and Their Exponents:
Begin by noting the exponents of the variables inside the square root. For example, in the expression \( \sqrt{x^8 y^4} \), the exponents are 8 for \( x \) and 4 for \( y \). -
Express Exponents as Products of Two:
Break down the exponents into products of two to identify perfect squares. For example, \( x^8 = (x^4)^2 \) and \( y^4 = (y^2)^2 \). -
Rewrite the Expression:
Rewrite the expression under the square root using these perfect squares. For example, \( \sqrt{x^8 y^4} = \sqrt{(x^4)^2 (y^2)^2} \). -
Apply the Square Root to Each Term:
Use the property of square roots \( \sqrt{a^2} = a \) to simplify each term. This results in \( x^4 y^2 \) for our example. -
Combine the Results:
Combine the simplified terms to get the final answer. For the example \( \sqrt{x^8 y^4} \), the result is \( x^4 y^2 \).
This method ensures that you correctly simplify square roots involving variables by handling the exponents effectively.
Simplifying Square Roots of Monomials
Simplifying square roots of monomials involves breaking down the expression under the radical sign into its prime factors and identifying perfect squares. This process can be simplified using exponents and properties of radicals.
- Identify Perfect Squares: Look for perfect square factors in the numerical coefficient and the variables.
- Prime Factorization: Break down the numerical coefficient and variables into their prime factors.
- Group Factors: Group the prime factors into pairs of identical factors. For variables, use the property \(a^2 = a \times a\).
- Rewrite as Perfect Squares: Rewrite these pairs as perfect squares. For example, \(x^6\) can be written as \((x^3)^2\).
- Simplify the Radicals: Take the square root of the perfect squares. For instance, \(\sqrt{(x^3)^2} = x^3\).
- Combine Results: Combine the simplified factors outside the radical. Use the property \(\sqrt{a^2} = |a|\) to ensure positive results.
Let's go through an example to illustrate the process:
- Example: Simplify \(\sqrt{49x^{10}y^{8}}\).
- Step 1: Identify perfect squares: \(49\), \(x^{10}\), and \(y^{8}\).
- Step 2: Rewrite these as squares: \(49 = 7^2\), \(x^{10} = (x^5)^2\), \(y^{8} = (y^4)^2\).
- Step 3: Separate into individual radicals: \(\sqrt{7^2}\cdot \sqrt{(x^5)^2}\cdot \sqrt{(y^4)^2}\).
- Step 4: Simplify the radicals: \(7 \cdot |x^5| \cdot |y^4|\).
- Step 5: Combine results: \(7|x^5|y^4\).
Thus, \(\sqrt{49x^{10}y^{8}} = 7|x^5|y^4\). This method can be applied to any monomial under the square root to simplify it effectively.
Examples of Simplifying Square Roots with Single Variables
Simplifying square roots with single variables follows the same principles as simplifying numerical square roots. The goal is to express the variable inside the square root as a product of squares, which can then be simplified.
Here are a few examples:
Example 1: Simplifying \(\sqrt{x^4}\)
Since \(x^4\) is a perfect square, it can be simplified directly:
\[\sqrt{x^4} = x^2\]
Example 2: Simplifying \(\sqrt{x^5}\)
In this case, split the exponent so that it contains a perfect square:
\[\sqrt{x^5} = \sqrt{x^4 \cdot x} = \sqrt{x^4} \cdot \sqrt{x} = x^2 \cdot \sqrt{x}\]
Example 3: Simplifying \(\sqrt{25x^2}\)
Both 25 and \(x^2\) are perfect squares:
\[\sqrt{25x^2} = \sqrt{25} \cdot \sqrt{x^2} = 5x\]
Example 4: Simplifying \(\sqrt{50x^3}\)
Factor the numerical part and the variable part separately:
\[\sqrt{50x^3} = \sqrt{25 \cdot 2 \cdot x^2 \cdot x} = \sqrt{25} \cdot \sqrt{2} \cdot \sqrt{x^2} \cdot \sqrt{x} = 5x\sqrt{2x}\]
Example 5: Simplifying \(\sqrt{y^8}\)
Since \(y^8\) is a perfect square, it can be simplified directly:
\[\sqrt{y^8} = y^4\]
Example 6: Simplifying \(\sqrt{81a^6}\)
Both 81 and \(a^6\) are perfect squares:
\[\sqrt{81a^6} = \sqrt{81} \cdot \sqrt{a^6} = 9a^3\]
In these examples, we see that the key steps are to identify and separate perfect square factors. This method can be applied to any variable expression within a square root.
Examples of Simplifying Square Roots with Multiple Variables
Simplifying square roots that contain multiple variables follows similar steps as simplifying those with single variables, but it involves additional factors. Here are detailed examples to illustrate the process:
Example 1: Simplifying \( \sqrt{50x^4y^6} \)
- Factor the radicand into prime factors and identify perfect squares:
\( 50x^4y^6 = 2 \cdot 5^2 \cdot x^4 \cdot y^6 \)
- Rewrite the radicand to show the perfect squares:
\( \sqrt{50x^4y^6} = \sqrt{2 \cdot 5^2 \cdot (x^2)^2 \cdot (y^3)^2} \)
- Separate the perfect squares from the radical:
\( \sqrt{2 \cdot 5^2 \cdot (x^2)^2 \cdot (y^3)^2} = 5 \cdot x^2 \cdot y^3 \cdot \sqrt{2} \)
- Simplify:
\( \sqrt{50x^4y^6} = 5x^2y^3\sqrt{2} \)
Example 2: Simplifying \( \sqrt{72x^8y^3} \)
- Factor the radicand into prime factors and identify perfect squares:
\( 72x^8y^3 = 2^3 \cdot 3^2 \cdot x^8 \cdot y^3 \)
- Rewrite the radicand to show the perfect squares:
\( \sqrt{72x^8y^3} = \sqrt{(2^3) \cdot 3^2 \cdot (x^4)^2 \cdot (y^1)^2 \cdot y} \)
- Separate the perfect squares from the radical:
\( \sqrt{(2^3) \cdot 3^2 \cdot (x^4)^2 \cdot (y^1)^2 \cdot y} = 3 \cdot x^4 \cdot y \cdot \sqrt{2 \cdot 2 \cdot y} \)
- Simplify:
\( \sqrt{72x^8y^3} = 6x^4y\sqrt{2y} \)
Example 3: Simplifying \( \sqrt{128x^5y^7} \)
- Factor the radicand into prime factors and identify perfect squares:
\( 128x^5y^7 = 2^7 \cdot x^5 \cdot y^7 \)
- Rewrite the radicand to show the perfect squares:
\( \sqrt{128x^5y^7} = \sqrt{(2^6) \cdot 2 \cdot (x^2)^2 \cdot x \cdot (y^3)^2 \cdot y} \)
- Separate the perfect squares from the radical:
\( \sqrt{(2^6) \cdot 2 \cdot (x^2)^2 \cdot x \cdot (y^3)^2 \cdot y} = 2^3 \cdot x^2 \cdot y^3 \cdot \sqrt{2 \cdot x \cdot y} \)
- Simplify:
\( \sqrt{128x^5y^7} = 8x^2y^3\sqrt{2xy} \)
Example 4: Simplifying \( \sqrt{81x^6y^10z^3} \)
- Factor the radicand into prime factors and identify perfect squares:
\( 81x^6y^10z^3 = 3^4 \cdot x^6 \cdot y^10 \cdot z^3 \)
- Rewrite the radicand to show the perfect squares:
\( \sqrt{81x^6y^10z^3} = \sqrt{(3^2)^2 \cdot (x^3)^2 \cdot (y^5)^2 \cdot z^2 \cdot z} \)
- Separate the perfect squares from the radical:
\( \sqrt{(3^2)^2 \cdot (x^3)^2 \cdot (y^5)^2 \cdot z^2 \cdot z} = 3^2 \cdot x^3 \cdot y^5 \cdot \sqrt{z^2 \cdot z} \)
- Simplify:
\( \sqrt{81x^6y^10z^3} = 9x^3y^5\sqrt{z} \)

Simplifying Square Roots Involving Fractions
When simplifying square roots involving fractions, the goal is to reduce the fraction to its simplest form. Here are the steps to simplify these types of square roots:
Step-by-Step Process
-
Identify and Simplify the Square Root:
Start by simplifying the square root in the numerator and the denominator separately. Look for perfect squares within the radicands.
Example: \(\sqrt{\frac{18}{50}}\)
Simplify \(\sqrt{18}\) and \(\sqrt{50}\):
\(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
\(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\)
So, \(\sqrt{\frac{18}{50}} = \frac{3\sqrt{2}}{5\sqrt{2}} = \frac{3}{5}\)
-
Rationalize the Denominator:
If the denominator contains a square root, rationalize it by multiplying both the numerator and the denominator by the conjugate of the denominator.
Example: \(\frac{5}{\sqrt{3}}\)
Multiply by \(\frac{\sqrt{3}}{\sqrt{3}}\):
\(\frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}\)
-
Combine and Simplify:
Combine the simplified square roots and rationalized fractions to get the final simplified form.
Example: \(\frac{2}{\sqrt{12}}\)
Simplify \(\sqrt{12}\):
\(\sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3}\)
Rationalize: \(\frac{2}{2\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{2\sqrt{3}}{6} = \frac{\sqrt{3}}{3}\)
Examples
-
Simplify \(\sqrt{\frac{27}{8}}\):
Simplify the numerator and the denominator:
\(\sqrt{27} = \sqrt{9 \times 3} = 3\sqrt{3}\)
\(\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}\)
So, \(\sqrt{\frac{27}{8}} = \frac{3\sqrt{3}}{2\sqrt{2}}\)
Rationalize the denominator:
\(\frac{3\sqrt{3}}{2\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{3\sqrt{6}}{4}\)
-
Simplify \(\frac{\sqrt{45}}{5}\):
Simplify the numerator:
\(\sqrt{45} = \sqrt{9 \times 5} = 3\sqrt{5}\)
So, \(\frac{\sqrt{45}}{5} = \frac{3\sqrt{5}}{5}\)
No further simplification is needed as the denominator is already rational.
By following these steps, you can simplify square roots involving fractions to their simplest forms, making them easier to work with in mathematical expressions.
Quotient Property of Square Roots
The quotient property of square roots states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. This property is useful when simplifying expressions involving square roots of fractions. Mathematically, it is expressed as:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}, \quad \text{where } b \ne 0\]
Let's go through a few examples to understand how to apply this property:
Example 1: Simplifying \(\sqrt{\frac{50}{2}}\)
- Identify the fraction under the square root: \(\sqrt{\frac{50}{2}}\).
- Apply the quotient property: \(\sqrt{\frac{50}{2}} = \frac{\sqrt{50}}{\sqrt{2}}\).
- Simplify the numerator and the denominator:
- The square root of 50 can be simplified to \(5\sqrt{2}\) (since \(50 = 25 \times 2\) and \(\sqrt{25} = 5\)).
- The square root of 2 remains \(\sqrt{2}\).
- Combine the results: \(\frac{5\sqrt{2}}{\sqrt{2}} = 5\).
Example 2: Simplifying \(\sqrt{\frac{18x^4}{2x}}\)
- Identify the fraction under the square root: \(\sqrt{\frac{18x^4}{2x}}\).
- Apply the quotient property: \(\sqrt{\frac{18x^4}{2x}} = \frac{\sqrt{18x^4}}{\sqrt{2x}}\).
- Simplify the numerator and the denominator:
- The square root of 18 can be simplified to \(3\sqrt{2}\) (since \(18 = 9 \times 2\) and \(\sqrt{9} = 3\)).
- The square root of \(x^4\) is \(x^2\).
- The square root of \(2x\) is \(\sqrt{2x}\).
- Combine the results: \(\frac{3x^2\sqrt{2}}{\sqrt{2x}} = \frac{3x^2\sqrt{2}}{\sqrt{2}\sqrt{x}} = \frac{3x^2}{\sqrt{x}} = 3x\sqrt{x}\).
Example 3: Simplifying \(\sqrt{\frac{45a^6}{5a^2}}\)
- Identify the fraction under the square root: \(\sqrt{\frac{45a^6}{5a^2}}\).
- Apply the quotient property: \(\sqrt{\frac{45a^6}{5a^2}} = \frac{\sqrt{45a^6}}{\sqrt{5a^2}}\).
- Simplify the numerator and the denominator:
- The square root of 45 can be simplified to \(3\sqrt{5}\) (since \(45 = 9 \times 5\) and \(\sqrt{9} = 3\)).
- The square root of \(a^6\) is \(a^3\).
- The square root of 5 remains \(\sqrt{5}\).
- The square root of \(a^2\) is \(a\).
- Combine the results: \(\frac{3a^3\sqrt{5}}{\sqrt{5}a} = \frac{3a^3}{a} = 3a^2\).
Using the quotient property of square roots simplifies the process of dealing with square roots of fractions, making complex expressions more manageable.
Examples of Simplifying Square Roots of Fractions
Simplifying square roots of fractions involves applying the quotient property of square roots, which states:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
Let's go through some examples step by step:
-
Simplify \(\sqrt{\frac{49}{64}}\):
- Apply the quotient property: \(\sqrt{\frac{49}{64}} = \frac{\sqrt{49}}{\sqrt{64}}\)
- Calculate the square roots: \(\sqrt{49} = 7\) and \(\sqrt{64} = 8\)
- Combine the results: \(\frac{\sqrt{49}}{\sqrt{64}} = \frac{7}{8}\)
- So, \(\sqrt{\frac{49}{64}} = \frac{7}{8}\)
-
Simplify \(\sqrt{\frac{18}{50}}\):
- Reduce the fraction under the radical first: \(\frac{18}{50} = \frac{9}{25}\)
- Apply the quotient property: \(\sqrt{\frac{9}{25}} = \frac{\sqrt{9}}{\sqrt{25}}\)
- Calculate the square roots: \(\sqrt{9} = 3\) and \(\sqrt{25} = 5\)
- Combine the results: \(\frac{\sqrt{9}}{\sqrt{25}} = \frac{3}{5}\)
- So, \(\sqrt{\frac{18}{50}} = \frac{3}{5}\)
-
Simplify \(\sqrt{1\frac{13}{36}}\):
- Convert the mixed number to an improper fraction: \(1\frac{13}{36} = \frac{49}{36}\)
- Apply the quotient property: \(\sqrt{\frac{49}{36}} = \frac{\sqrt{49}}{\sqrt{36}}\)
- Calculate the square roots: \(\sqrt{49} = 7\) and \(\sqrt{36} = 6\)
- Combine the results: \(\frac{\sqrt{49}}{\sqrt{36}} = \frac{7}{6}\)
- So, \(\sqrt{1\frac{13}{36}} = \frac{7}{6} = 1\frac{1}{6}\)
-
Simplify \(\sqrt{\frac{25}{36}}\):
- Apply the quotient property: \(\sqrt{\frac{25}{36}} = \frac{\sqrt{25}}{\sqrt{36}}\)
- Calculate the square roots: \(\sqrt{25} = 5\) and \(\sqrt{36} = 6\)
- Combine the results: \(\frac{\sqrt{25}}{\sqrt{36}} = \frac{5}{6}\)
- So, \(\sqrt{\frac{25}{36}} = \frac{5}{6}\)
By following these steps and applying the quotient property of square roots, you can simplify square roots of fractions effectively.
Handling Even and Odd Exponents in Variables
Simplifying square roots involving variables with even and odd exponents follows specific rules. Here’s a detailed guide:
Even Exponents:
When the exponent of a variable under a square root is even, you can simply divide the exponent by 2 to simplify.
- Example: Simplify \( \sqrt{x^8} \)
- Since 8 is even, divide the exponent by 2: \( \sqrt{x^8} = x^{8/2} = x^4 \)
Odd Exponents:
When the exponent of a variable under a square root is odd, rewrite it as the product of an even exponent and 1.
- Example: Simplify \( \sqrt{x^9} \)
- Rewrite \( x^9 \) as \( x^8 \cdot x \)
- Apply the square root: \( \sqrt{x^9} = \sqrt{x^8 \cdot x} = \sqrt{x^8} \cdot \sqrt{x} = x^4 \sqrt{x} \)
Examples:
- Simplify \( \sqrt{x^{12} y^6} \)
- Both exponents are even: \( \sqrt{x^{12} y^6} = x^{12/2} y^{6/2} = x^6 y^3 \)
- Simplify \( \sqrt{x^{7} y^5} \)
- Rewrite each variable: \( x^7 = x^6 \cdot x \) and \( y^5 = y^4 \cdot y \)
- Simplify: \( \sqrt{x^7 y^5} = \sqrt{x^6 \cdot x \cdot y^4 \cdot y} = \sqrt{x^6} \cdot \sqrt{x} \cdot \sqrt{y^4} \cdot \sqrt{y} = x^3 \cdot \sqrt{x} \cdot y^2 \cdot \sqrt{y} = x^3 y^2 \sqrt{xy} \)
- Simplify \( \sqrt{a^{10} b^{9}} \)
- Rewrite \( b^9 \): \( a^{10} = a^{10} \) (even) and \( b^9 = b^8 \cdot b \) (odd)
- Simplify: \( \sqrt{a^{10} b^{9}} = \sqrt{a^{10}} \cdot \sqrt{b^8} \cdot \sqrt{b} = a^5 \cdot b^4 \cdot \sqrt{b} = a^5 b^4 \sqrt{b} \)
These steps ensure a systematic approach to handling even and odd exponents in variables under square roots, making the simplification process straightforward.
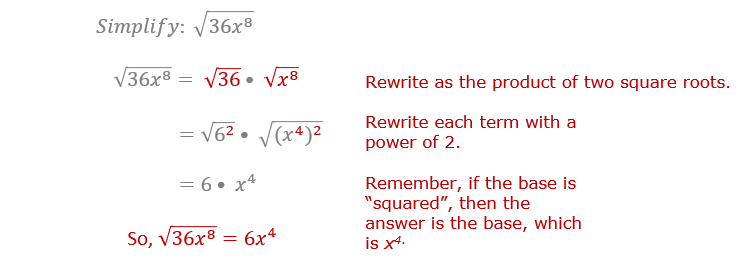
Common Mistakes and How to Avoid Them
When simplifying square roots with variables, it's important to avoid common mistakes to ensure accurate results. Here are some common errors and tips on how to avoid them:
-
Overlooking Perfect Squares:
Always check for perfect squares within the radicand. Recognizing and factoring out these perfect squares simplifies the process significantly.
-
Misapplying Properties:
Ensure correct application of the product and quotient properties. For instance, remember that \(\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}\) and \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\), but \(\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}\).
-
Ignoring Variables:
When dealing with variables, identify and simplify perfect square factors. For example, \(\sqrt{x^4} = x^2\), since \(x^4\) is a perfect square.
-
Arithmetic Errors:
Double-check your arithmetic operations, such as factorization and multiplication, to avoid mistakes in the simplification process.
-
Forgetting to Rationalize the Denominator:
Leaving a square root in the denominator is often considered incomplete. To rationalize the denominator, multiply the numerator and the denominator by the conjugate of the denominator if necessary.
Avoiding these common mistakes requires careful attention and practice. By following these tips, you can enhance your ability to simplify square roots accurately and efficiently.
Practice Problems and Solutions
Here are some practice problems to help you master the skill of simplifying square roots with variables. Each problem is followed by a detailed solution to guide you through the process.
-
Problem 1: Simplify \( \sqrt{50x^4} \)
Solution:
- Prime factorize the number and separate the variables: \( \sqrt{50x^4} = \sqrt{25 \cdot 2 \cdot x^4} \)
- Rewrite using perfect squares: \( \sqrt{25 \cdot 2 \cdot x^4} = \sqrt{25} \cdot \sqrt{2} \cdot \sqrt{x^4} \)
- Simplify each part: \( 5 \cdot \sqrt{2} \cdot x^2 \)
- Final simplified form: \( 5x^2\sqrt{2} \)
-
Problem 2: Simplify \( \sqrt{18y^3} \)
Solution:
- Prime factorize the number and separate the variables: \( \sqrt{18y^3} = \sqrt{9 \cdot 2 \cdot y^3} \)
- Rewrite using perfect squares: \( \sqrt{9 \cdot 2 \cdot y^3} = \sqrt{9} \cdot \sqrt{2} \cdot \sqrt{y^2 \cdot y} \)
- Simplify each part: \( 3 \cdot \sqrt{2} \cdot y \cdot \sqrt{y} \)
- Final simplified form: \( 3y\sqrt{2y} \)
-
Problem 3: Simplify \( \sqrt{72a^6b^2} \)
Solution:
- Prime factorize the number and separate the variables: \( \sqrt{72a^6b^2} = \sqrt{36 \cdot 2 \cdot a^6 \cdot b^2} \)
- Rewrite using perfect squares: \( \sqrt{36 \cdot 2 \cdot a^6 \cdot b^2} = \sqrt{36} \cdot \sqrt{2} \cdot \sqrt{a^6} \cdot \sqrt{b^2} \)
- Simplify each part: \( 6 \cdot \sqrt{2} \cdot a^3 \cdot b \)
- Final simplified form: \( 6a^3b\sqrt{2} \)
-
Problem 4: Simplify \( \sqrt{\frac{45x^8}{5x^2}} \)
Solution:
- Simplify the fraction inside the square root: \( \sqrt{\frac{45x^8}{5x^2}} = \sqrt{9x^6} \)
- Rewrite using perfect squares: \( \sqrt{9x^6} = \sqrt{9} \cdot \sqrt{x^6} \)
- Simplify each part: \( 3 \cdot x^3 \)
- Final simplified form: \( 3x^3 \)
-
Problem 5: Simplify \( \sqrt{\frac{50a^5}{2a}} \)
Solution:
- Simplify the fraction inside the square root: \( \sqrt{\frac{50a^5}{2a}} = \sqrt{25a^4} \)
- Rewrite using perfect squares: \( \sqrt{25a^4} = \sqrt{25} \cdot \sqrt{a^4} \)
- Simplify each part: \( 5 \cdot a^2 \)
- Final simplified form: \( 5a^2 \)
Advanced Techniques for Complex Expressions
When simplifying square roots with complex expressions involving variables, it is essential to understand how to handle exponents, coefficients, and multiple variables. Here are some advanced techniques to simplify these expressions:
- Factorization: Break down both the numerical and variable parts into their prime factors. This helps in identifying perfect squares.
- Pairing Factors: Group identical factors into pairs. Each pair can be taken out of the square root as a single factor.
- Using Exponents: For variables, write exponents in terms of even powers to easily take the square root. For example, \(x^6\) can be written as \((x^3)^2\).
Examples
Here are some examples to illustrate these techniques:
- Simplify \( \sqrt{18x^4y^6} \):
- Factorize inside the square root: \(18 = 2 \cdot 3^2\), \(x^4 = (x^2)^2\), and \(y^6 = (y^3)^2\).
- Rewrite: \( \sqrt{2 \cdot 3^2 \cdot (x^2)^2 \cdot (y^3)^2} \).
- Simplify by taking the square root of each squared term: \(3 \cdot x^2 \cdot y^3 \sqrt{2} \).
- Final answer: \(3x^2y^3 \sqrt{2}\).
- Simplify \( \sqrt{50x^5y^7} \):
- Factorize: \(50 = 2 \cdot 5^2\), \(x^5 = x^4 \cdot x = (x^2)^2 \cdot x\), and \(y^7 = y^6 \cdot y = (y^3)^2 \cdot y\).
- Rewrite: \( \sqrt{2 \cdot 5^2 \cdot (x^2)^2 \cdot x \cdot (y^3)^2 \cdot y} \).
- Simplify: \(5x^2y^3 \sqrt{2xy} \).
- Final answer: \(5x^2y^3 \sqrt{2xy}\).
- Simplify \( \sqrt{72x^3y^5} \):
- Factorize: \(72 = 2^3 \cdot 3^2\), \(x^3 = x^2 \cdot x\), and \(y^5 = y^4 \cdot y = (y^2)^2 \cdot y\).
- Rewrite: \( \sqrt{2^3 \cdot 3^2 \cdot x^2 \cdot x \cdot (y^2)^2 \cdot y} \).
- Simplify: \(6xy^2 \sqrt{2xy} \).
- Final answer: \(6xy^2 \sqrt{2xy}\).
These advanced techniques require a good understanding of factorization, exponents, and the properties of square roots. With practice, you can simplify even the most complex expressions efficiently.
Summary and Key Takeaways
In this comprehensive guide, we explored various aspects of simplifying square roots with variables. Here are the key takeaways:
- Understanding Square Roots and Radicals: Square roots represent a number which, when multiplied by itself, gives the original number. Radicals are used to denote roots, with the square root being the most common.
- Basic Steps for Simplifying Square Roots: The general approach includes factoring the radicand (the number inside the radical), identifying pairs of factors, and simplifying them outside the radical.
- Prime Factorization and Perfect Squares: Breaking down the radicand into its prime factors helps in identifying perfect squares, which can be simplified easily.
- Using Exponents in Simplification: Exponents simplify the process of dealing with repeated multiplication. For instance, \(\sqrt{x^6}\) simplifies to \(x^3\) because \(6\) is an even exponent.
- Simplifying Square Roots of Monomials: For expressions like \(\sqrt{ax^n}\), separate the constant and the variable parts. Simplify the constants and apply the square root to the exponents.
- Examples of Simplifying Square Roots with Variables: Through examples, we illustrated how to break down complex expressions and simplify them step-by-step.
- Examples of Simplifying Square Roots with Multiple Variables: Handling multiple variables involves similar steps but requires careful attention to each variable's exponent.
- Simplifying Square Roots Involving Fractions: Use the Quotient Property of square roots to simplify fractions. This property states \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- Handling Even and Odd Exponents in Variables: For even exponents, the variable can be simplified completely outside the radical. For odd exponents, factor out the highest even number and leave the remaining variable inside the radical.
- Common Mistakes and How to Avoid Them: Be cautious about incorrectly factoring or simplifying terms. Always verify by squaring your result to see if it matches the original expression.
- Practice Problems and Solutions: Regular practice is essential. We provided various problems with step-by-step solutions to reinforce understanding.
- Advanced Techniques for Complex Expressions: For more complex expressions, combining multiple simplification techniques, such as prime factorization, exponent rules, and the Quotient Property, is necessary.
In conclusion, simplifying square roots with variables requires a solid understanding of basic mathematical principles and consistent practice. By mastering these techniques, you can simplify even the most complex expressions with confidence.

Video này hướng dẫn cách đơn giản hoá căn bậc hai với biến số, giúp bạn hiểu rõ hơn về chủ đề này trong toán học.
Căn Bậc Hai Với Biến (Đơn Giản Hoá Toán Học)
READ MORE:
Video này hướng dẫn cách đơn giản hoá căn bậc hai với biến số, giúp bạn nắm vững kiến thức và ứng dụng trong toán học.
Đơn Giản Hoá Căn Bậc Hai Với Biến