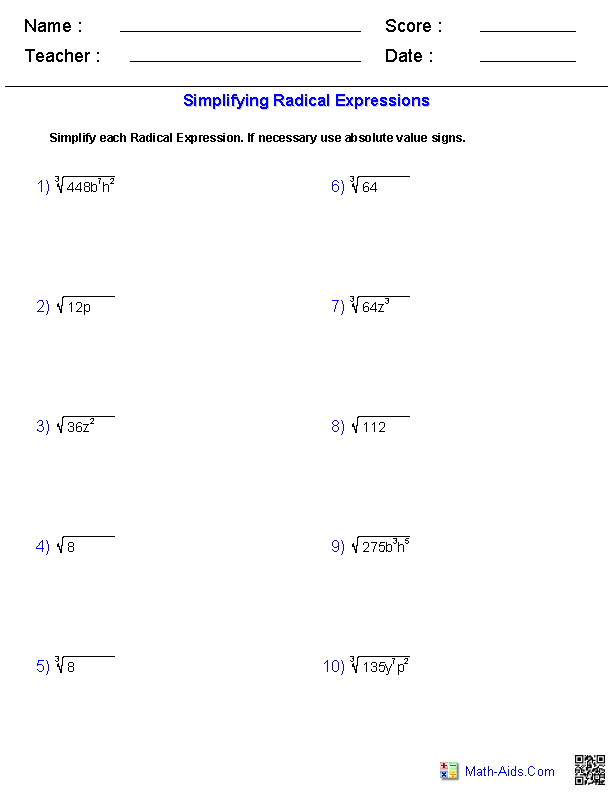Topic simplifying radical expressions exponents: Understanding how to simplify radical expressions and exponents is crucial for mastering algebra. This article breaks down the essential rules and steps, helping you tackle these mathematical challenges with confidence and ease. Explore the fundamental properties and techniques to simplify expressions efficiently.
Table of Content
- Simplifying Radical Expressions and Exponents
- Introduction to Simplifying Radical Expressions
- Basic Concepts and Definitions
- Rules for Simplifying Radical Expressions
- Product and Quotient Rule for Radicals
- Simplifying Radicals with Variables
- Simplifying Radical Expressions Using Exponents
- Prime Factorization Method
- Examples and Step-by-Step Solutions
- Simplifying Higher-Order Roots
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- Additional Resources for Mastery
- YOUTUBE: Hướng dẫn đơn giản hóa biểu thức căn bậc với các biến để thu hút người xem.
Simplifying Radical Expressions and Exponents
Radical expressions can often be simplified by applying rules and properties of exponents. Below are some key techniques and examples to help understand the process of simplifying radical expressions.
Basic Rules for Simplifying Radicals
\(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\) \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}, \, b \neq 0\) \(\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}\) \(\sqrt{a} - \sqrt{b} \neq \sqrt{a - b}\)
Steps to Simplify Radical Expressions
- Rewrite the number under the radical as a product of its prime factors.
- Combine the factors in pairs of identical factors.
- Bring out the factors with powers of 2 from under the radical.
- Simplify the expression until no further simplification is possible.
Examples of Simplifying Radical Expressions
Example 1: Simplify \(\sqrt{100x^4y^6z^3}\)
Step-by-step solution:
Example 2: Simplify \(\frac{\sqrt{12}}{\sqrt{5}}\)
Step-by-step solution:
Example 3: Simplify \(\sqrt[3]{40m^5}\)
Step-by-step solution:
Working with Rational Exponents
Rational exponents provide another method to simplify radicals:
\(\sqrt[n]{a^x} = a^{\frac{x}{n}}\)
For example:
Conclusion
By following these rules and steps, you can simplify complex radical expressions and exponents effectively, making it easier to work with these types of mathematical problems.

READ MORE:
Introduction to Simplifying Radical Expressions
Simplifying radical expressions involves breaking down complex expressions into their simplest forms by using various mathematical rules and properties. This process helps in making calculations easier and more comprehensible. Here are some key steps and concepts involved in simplifying radical expressions:
-
Identify Perfect Powers:
Look for perfect square factors (for square roots) or perfect cube factors (for cube roots) in the radicand. For example, in the expression \(\sqrt{50}\), you can rewrite \(50\) as \(25 \times 2\), which simplifies to \(5\sqrt{2}\).
-
Use the Product Property of Radicals:
The product property states that \(\sqrt[n]{a \cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b}\). This property allows you to split a radical into two or more simpler radicals, making it easier to simplify. For example, \(\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}\).
-
Use the Quotient Property of Radicals:
The quotient property states that \(\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}\). This is useful for simplifying radicals involving fractions. For instance, \(\sqrt{\frac{16}{25}} = \frac{\sqrt{16}}{\sqrt{25}} = \frac{4}{5}\).
-
Simplify Exponents:
When dealing with expressions that have exponents, such as \(\sqrt{x^4}\), you can simplify them by recognizing that \(\sqrt{x^4} = x^2\). This is because \(x^4\) is a perfect square.
-
Combine Like Terms:
If you have multiple radical terms, combine them if they have the same radicand. For example, \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\).
By mastering these steps and properties, you can simplify complex radical expressions efficiently, making them easier to work with in mathematical problems and real-world applications.
Basic Concepts and Definitions
In order to simplify radical expressions and exponents, it's essential to understand the basic concepts and definitions. This section covers the key principles you need to grasp.
A radical expression is any expression containing a radical (√) symbol. For example, \(\sqrt{a}\) is a radical expression where \(a\) is called the radicand. The most common types of radicals are square roots and cube roots, but higher-order roots also exist.
Properties of Radicals
- Product Property: \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \(b \neq 0\)
Simplifying Radical Expressions
- Identify any perfect square (or cube, etc.) factors in the radicand.
- Rewrite the radicand as the product of its factors.
- Apply the product property to split the radical into simpler parts.
- Simplify each part of the expression.
For example, to simplify \(\sqrt{72}\), we can write it as \(\sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\).
Rational Exponents
Rational exponents are another way to represent roots. For instance, \(a^{1/n} = \sqrt[n]{a}\). This notation can simplify the manipulation of expressions involving roots and powers.
Example: Simplify \(x^{2/3}\).
- Rewrite using radical notation: \(x^{2/3} = \sqrt[3]{x^2}\).
- This expression means taking the cube root of \(x^2\).
Combining Like Terms
When simplifying radical expressions, combine like terms by ensuring the radicands and the order of the roots are the same.
Example: Simplify \(3\sqrt{2} + 2\sqrt{2}\).
- Since the radicands are identical, combine the coefficients: \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\).
Understanding these fundamental concepts and properties will help you simplify radical expressions and work with rational exponents effectively.
Rules for Simplifying Radical Expressions
Understanding the rules for simplifying radical expressions is crucial for solving mathematical problems involving roots. Below are the key rules and methods you should know:
-
Product Rule for Radicals:
If \(a \ge 0\) and \(b \ge 0\), then \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\).
Example: \(\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}\).
-
Quotient Rule for Radicals:
If \(a \ge 0\) and \(b > 0\), then \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
Example: \(\sqrt{\frac{50}{2}} = \frac{\sqrt{50}}{\sqrt{2}} = \frac{5\sqrt{2}}{\sqrt{2}} = 5\).
-
Simplifying Radicals Using Prime Factorization:
Break down the number inside the radical into its prime factors and simplify by pairing the prime factors.
Example: \(\sqrt{72} = \sqrt{2^3 \cdot 3^2} = 3\sqrt{2}\).
-
Simplifying Radicals with Variables:
For variables under the radical, use the property that \(\sqrt{x^2} = |x|\) and simplify accordingly.
Example: \(\sqrt{12x^4y^2} = \sqrt{4 \cdot 3 \cdot x^4 \cdot y^2} = 2x^2y\sqrt{3}\).
-
Combining Like Radicals:
Radicals can be combined if they have the same radicand. This is similar to combining like terms in algebra.
Example: \(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\).
-
Converting Radicals to Exponents:
Use the property that \(\sqrt[n]{a} = a^{1/n}\) to convert radicals to exponents, which can make simplifying expressions easier.
Example: \(\sqrt[3]{a^2 b^4} = b \sqrt[3]{a^2b}\).
These rules are fundamental for working with radical expressions. By mastering them, you can simplify complex expressions and solve equations more efficiently.
Product and Quotient Rule for Radicals
When simplifying radical expressions, two essential rules to remember are the product rule and the quotient rule. These rules allow us to break down more complex radicals into simpler components, making them easier to work with.
Product Rule for Radicals
The product rule for radicals states that the square root of a product is equal to the product of the square roots of each factor. In mathematical terms, this can be expressed as:
\[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \]
For example, consider the expression \( \sqrt{50} \). Using the product rule, we can simplify it as follows:
- Find the largest factor of 50 that is a perfect square: \( 50 = 25 \cdot 2 \).
- Apply the product rule: \( \sqrt{50} = \sqrt{25 \cdot 2} \).
- Simplify each radical: \( \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2} \).
Quotient Rule for Radicals
The quotient rule for radicals states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. This can be expressed as:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
For example, to simplify the expression \( \sqrt{\frac{49}{9}} \), follow these steps:
- Apply the quotient rule: \( \sqrt{\frac{49}{9}} = \frac{\sqrt{49}}{\sqrt{9}} \).
- Simplify each radical: \( \frac{\sqrt{49}}{\sqrt{9}} = \frac{7}{3} \).
Examples
Here are more examples to illustrate the product and quotient rules:
- Product Rule Example:
- Rewrite 72 as a product of the largest perfect square: \( 72 = 36 \cdot 2 \).
- Apply the product rule: \( \sqrt{72} = \sqrt{36 \cdot 2} \).
- Simplify each radical: \( \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2} \).
- Quotient Rule Example:
- Apply the quotient rule: \( \sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} \).
- Simplify each radical: \( \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} \).
Simplify \( \sqrt{72} \):
Simplify \( \sqrt{\frac{25}{4}} \):

Simplifying Radicals with Variables
Simplifying radicals with variables follows similar rules as simplifying numerical radicals. The key is to treat the variables and numbers separately and apply the properties of radicals. Here are the steps and rules to follow:
Steps to Simplify Radicals with Variables
- Identify Perfect Square Factors
Look for perfect square factors in both the numerical and variable parts of the radical.
- Apply the Product Rule for Radicals
Use the property \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) to separate the factors under the radical.
- Simplify the Variables
For variables with even exponents, use the property \(\sqrt{x^{2k}} = x^k\). For odd exponents, separate them into a product of an even exponent and the leftover variable.
- Combine Like Terms
Combine the simplified numerical and variable parts outside the radical.
Examples
Let's look at some examples to illustrate these steps:
Example 1: Simplify \(\sqrt{50x^4y^2}\)
Step-by-step solution:
- Identify the perfect square factors: \(50 = 25 \cdot 2\), \(x^4 = (x^2)^2\), and \(y^2 = (y)^2\).
- Apply the product rule: \(\sqrt{50x^4y^2} = \sqrt{25} \cdot \sqrt{2} \cdot \sqrt{x^4} \cdot \sqrt{y^2}\).
- Simplify the variables and numbers: \(5 \cdot \sqrt{2} \cdot x^2 \cdot y\).
- Combine the terms: \(5x^2y\sqrt{2}\).
Thus, \(\sqrt{50x^4y^2} = 5x^2y\sqrt{2}\).
Example 2: Simplify \(\sqrt{72x^5y^7}\)
Step-by-step solution:
- Identify the perfect square factors: \(72 = 36 \cdot 2\), \(x^5 = x^4 \cdot x\), and \(y^7 = y^6 \cdot y\).
- Apply the product rule: \(\sqrt{72x^5y^7} = \sqrt{36} \cdot \sqrt{2} \cdot \sqrt{x^4} \cdot \sqrt{x} \cdot \sqrt{y^6} \cdot \sqrt{y}\).
- Simplify the variables and numbers: \(6 \cdot \sqrt{2} \cdot x^2 \cdot \sqrt{x} \cdot y^3 \cdot \sqrt{y}\).
- Combine the terms: \(6x^2y^3\sqrt{2xy}\).
Thus, \(\sqrt{72x^5y^7} = 6x^2y^3\sqrt{2xy}\).
Key Takeaways
- Always separate the numerical and variable parts when simplifying radicals.
- Use the properties of exponents and radicals to simplify the variables inside the radical.
- Combine all simplified parts to get the final simplified radical expression.
Simplifying Radical Expressions Using Exponents
Simplifying radical expressions using exponents involves converting radicals to expressions with fractional exponents. This approach allows us to leverage the rules of exponents to simplify the expressions effectively.
Basic Concept
Any radical expression can be rewritten using fractional exponents. The general form is:
\[ \sqrt[n]{a^m} = a^{\frac{m}{n}} \]
Where:
- \( a \) is the base.
- \( m \) is the exponent under the radical.
- \( n \) is the index of the radical.
Examples
Let's look at a few examples to understand this concept better:
-
Example 1: Simplify \( \sqrt{x} \)
Using the fractional exponent form:
\[ \sqrt{x} = x^{\frac{1}{2}} \] -
Example 2: Simplify \( \sqrt[3]{y^2} \)
Using the fractional exponent form:
\[ \sqrt[3]{y^2} = y^{\frac{2}{3}} \] -
Example 3: Simplify \( \sqrt[4]{16} \)
Using the fractional exponent form:
\[ \sqrt[4]{16} = 16^{\frac{1}{4}} \]Since \( 16 = 2^4 \), we can simplify further:
\[ 16^{\frac{1}{4}} = (2^4)^{\frac{1}{4}} = 2 \]
Steps to Simplify Using Exponents
- Convert the radical expression to a fractional exponent.
- Apply the rules of exponents to simplify the expression.
- If needed, convert back to radical form for the final simplified expression.
Rules of Exponents
Here are some key exponent rules that are useful when simplifying radical expressions:
- Product of Powers: \( a^m \cdot a^n = a^{m+n} \)
- Quotient of Powers: \( \frac{a^m}{a^n} = a^{m-n} \)
- Power of a Power: \( (a^m)^n = a^{m \cdot n} \)
- Power of a Product: \( (ab)^m = a^m \cdot b^m \)
- Power of a Quotient: \( \left(\frac{a}{b}\right)^m = \frac{a^m}{b^m} \)
Practice Problems
Here are a few practice problems to apply what you've learned:
- Convert \( \sqrt[5]{x^3} \) to an expression with a fractional exponent.
- Simplify \( (x^{\frac{3}{4}})^2 \).
- Write \( \sqrt[6]{y^2} \) as a radical expression with a fractional exponent.
Answers:
- \( x^{\frac{3}{5}} \)
- \( x^{\frac{3}{2}} \)
- \( y^{\frac{1}{3}} \)
Prime Factorization Method
The prime factorization method is a powerful technique for simplifying radical expressions, especially useful when dealing with square roots. The process involves breaking down the radicand (the number inside the radical) into its prime factors and then simplifying the expression by grouping these factors.
-
Step 1: Factor the Radicand into Prime Numbers
Start by expressing the number under the radical as a product of prime factors. For example, to simplify \( \sqrt{72} \), break down 72 into its prime factors:
- 72 can be factored into \( 2 \times 36 \)
- 36 can be factored into \( 2 \times 18 \)
- 18 can be factored into \( 2 \times 9 \)
- 9 can be factored into \( 3 \times 3 \)
So, the prime factors of 72 are \( 2 \times 2 \times 2 \times 3 \times 3 \).
-
Step 2: Group the Prime Factors
Next, group the prime factors in pairs. Each pair of the same number can be taken out of the square root:
- In the case of \( \sqrt{72} \): \( 2 \times 2 \times 2 \times 3 \times 3 \)
- Group them as: \( (2 \times 2) \times 2 \times (3 \times 3) \)
-
Step 3: Simplify the Expression
Take one number from each pair out of the radical and multiply them together:
- From \( (2 \times 2) \), take out one 2
- From \( (3 \times 3) \), take out one 3
So, \( \sqrt{72} \) simplifies to \( 2 \times 3 \times \sqrt{2} \). Therefore, \( \sqrt{72} = 6\sqrt{2} \).
This method can be extended to other radicals, including those with variables. For example, to simplify \( \sqrt{50x^2y^3} \):
-
Factor the radicand into prime numbers and variables:
\( 50x^2y^3 = 2 \times 5 \times 5 \times x \times x \times y \times y \times y \)
-
Group the factors:
\( (5 \times 5) \times x^2 \times (y \times y) \times y \)
-
Simplify by taking one number from each group out of the radical:
\( 5 \times x \times y \times \sqrt{2y} \)
Thus, \( \sqrt{50x^2y^3} = 5xy\sqrt{2y} \).
Using the prime factorization method ensures a systematic approach to simplifying radicals, making complex expressions more manageable.
Examples and Step-by-Step Solutions
Understanding how to simplify radical expressions is crucial for solving various mathematical problems. Here are some detailed examples and step-by-step solutions to help you master this concept:
Example 1: Simplifying \(\sqrt{72}\)
- Find the largest perfect square that divides into 72. The number is 36.
- Write 72 as the product of 36 and 2: \(72 = 36 \times 2\).
- Use the product rule: \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\).
Example 2: Simplifying \(\frac{\sqrt{50}}{\sqrt{2}}\)
- Combine the radicals: \(\frac{\sqrt{50}}{\sqrt{2}} = \sqrt{\frac{50}{2}}\).
- Simplify the fraction under the radical: \(\sqrt{\frac{50}{2}} = \sqrt{25} = 5\).
Example 3: Simplifying \(\sqrt[3]{54}\)
- Find the largest perfect cube that divides into 54. The number is 27.
- Write 54 as the product of 27 and 2: \(54 = 27 \times 2\).
- Use the product rule: \(\sqrt[3]{54} = \sqrt[3]{27 \times 2} = \sqrt[3]{27} \times \sqrt[3]{2} = 3\sqrt[3]{2}\).
Example 4: Simplifying \(\sqrt{8x^3y^3}\)
- Factor inside the radical: \(\sqrt{8x^3y^3} = \sqrt{2^3 \times x^2 \times x \times y^2 \times y}\).
- Group the factors to simplify: \(\sqrt{2^2 \times 2 \times x^2 \times x \times y^2 \times y} = 2xy \sqrt{2xy}\).
Example 5: Simplifying \(\frac{10b^2c^2}{c\sqrt{4b^3}}\)
- Simplify inside the radical: \(\frac{10b^2c^2}{c\sqrt{4b^3}} = \frac{10b^2c^2}{2c\sqrt{b^2b}}\).
- Further simplify: \(\frac{10b^2c^2}{2bc\sqrt{b}} = \frac{5bc}{\sqrt{b}} = \frac{5bc\sqrt{b}}{b} = 5c\sqrt{b}\).
Example 6: Simplifying \(\frac{\sqrt{12}}{\sqrt{5}}\)
- Combine the radicals: \(\frac{\sqrt{12}}{\sqrt{5}} = \sqrt{\frac{12}{5}}\).
- Rationalize the denominator by multiplying by \(\sqrt{5}\): \(\frac{\sqrt{12} \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}} = \frac{\sqrt{60}}{5} = \frac{\sqrt{4 \times 15}}{5} = \frac{2\sqrt{15}}{5}\).
These examples illustrate various techniques for simplifying radical expressions. Practice these steps to become proficient in handling more complex expressions.

Simplifying Higher-Order Roots
Simplifying higher-order roots involves using the same principles as simplifying square roots but applying them to cube roots, fourth roots, and so on. Here are the detailed steps for simplifying higher-order roots:
Steps to Simplify Higher-Order Roots
- Identify the Index:
Determine the index \( n \) of the root. For example, the cube root has an index of 3, the fourth root has an index of 4, and so on.
- Prime Factorization:
Find the prime factorization of the number or variable inside the radical. Break down the number into its prime factors.
Example: For \( \sqrt[3]{8} \), the prime factorization of 8 is \( 2^3 \).
- Group the Factors:
Group the prime factors according to the index. Each group of \( n \) identical factors can be taken out of the radical.
Example: \( \sqrt[3]{8} = \sqrt[3]{2^3} = 2 \).
- Simplify Variables:
For variables, apply the same process. If the exponent of the variable inside the radical is a multiple of the index, it can be simplified.
Example: \( \sqrt[4]{x^8} = \sqrt[4]{(x^2)^4} = x^2 \).
- Use the Product Property:
If the expression inside the radical is a product, use the product property of roots to simplify.
Example: \( \sqrt[3]{27a^6} = \sqrt[3]{27} \cdot \sqrt[3]{a^6} = 3a^2 \).
- Absolute Values for Even Roots:
For even roots, ensure the result is non-negative by using absolute values if necessary.
Example: \( \sqrt[4]{y^4} = |y| \).
Examples
- Simplify \( \sqrt[3]{64p^6} \):
Rewrite the radicand: \( 64p^6 = (4p^2)^3 \)
Apply the cube root: \( \sqrt[3]{(4p^2)^3} = 4p^2 \) - Simplify \( \sqrt[4]{81q^{12}} \):
Rewrite the radicand: \( 81q^{12} = (3q^3)^4 \)
Apply the fourth root: \( \sqrt[4]{(3q^3)^4} = 3|q^3| \) - Simplify \( \sqrt[5]{c^{10}} \):
Rewrite the radicand: \( c^{10} = (c^2)^5 \)
Apply the fifth root: \( \sqrt[5]{(c^2)^5} = c^2 \)
Common Mistakes and How to Avoid Them
Simplifying radical expressions can be tricky, and there are common mistakes that students often make. Here are some of the most frequent errors and tips on how to avoid them:
- Incorrect Application of the Product Rule:
Many students mistakenly believe that the square root of a sum is the sum of the square roots, i.e., \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\). This is not true. The correct rule is:
\(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\).
Example: \(\sqrt{4 \cdot 9} = \sqrt{36} = 6\), not \(\sqrt{4} + \sqrt{9} = 2 + 3 = 5\).
- Forgetting the Absolute Value:
When simplifying expressions that include variables, remember to account for the absolute value to ensure the result is non-negative. For example, \(\sqrt{x^2} = |x|\), not just \(x\).
Example: \(\sqrt{9x^2} = 3|x|\).
- Misinterpreting Radical Expressions with Fractions:
When dealing with fractions, students often forget to apply the radical to both the numerator and the denominator separately. The correct approach is:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \(b \neq 0\).
Example: \(\sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3}\).
- Improper Simplification of Higher-Order Roots:
When simplifying higher-order roots, students may incorrectly simplify the expression. For \(n\)-th roots, use:
\(\sqrt[n]{a^n} = a\), when \(a \geq 0\).
Example: \(\sqrt[3]{8y^3} = \sqrt[3]{(2y)^3} = 2y\).
- Ignoring the Need to Rationalize the Denominator:
When a radical is present in the denominator, it is often necessary to rationalize the denominator. Multiply both the numerator and the denominator by a suitable radical that will eliminate the radical in the denominator.
Example: To simplify \(\frac{\sqrt{2}}{\sqrt{3}}\), multiply by \(\frac{\sqrt{3}}{\sqrt{3}}\) to get \(\frac{\sqrt{2} \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{\sqrt{6}}{3}\).
By being aware of these common pitfalls and applying the correct rules, you can avoid mistakes and simplify radical expressions accurately.
Practice Problems and Solutions
Practicing simplifying radical expressions with exponents is essential for mastering these concepts. Below are a variety of practice problems along with detailed solutions to help you understand each step.
-
Problem 1: Simplify \(\sqrt{50}\)
Solution:
- Find the prime factorization of 50: \(50 = 2 \times 5^2\)
- Separate the factors inside the square root: \(\sqrt{50} = \sqrt{2 \times 5^2}\)
- Apply the square root to each factor: \(\sqrt{2} \times \sqrt{5^2}\)
- Simplify: \(\sqrt{2} \times 5 = 5\sqrt{2}\)
-
Problem 2: Simplify \(\sqrt[3]{54x^3}\)
Solution:
- Find the prime factorization of 54: \(54 = 2 \times 3^3\)
- Rewrite the expression inside the cube root: \(\sqrt[3]{54x^3} = \sqrt[3]{2 \times 3^3 \times x^3}\)
- Apply the cube root to each factor: \(\sqrt[3]{2} \times \sqrt[3]{3^3} \times \sqrt[3]{x^3}\)
- Simplify: \(\sqrt[3]{2} \times 3 \times x = 3x\sqrt[3]{2}\)
-
Problem 3: Simplify \(\sqrt[4]{81y^4}\)
Solution:
- Rewrite 81 as a power of 3: \(81 = 3^4\)
- Rewrite the expression inside the fourth root: \(\sqrt[4]{81y^4} = \sqrt[4]{3^4 y^4}\)
- Apply the fourth root to each factor: \(\sqrt[4]{3^4} \times \sqrt[4]{y^4}\)
- Simplify: \(3 \times y = 3y\)
-
Problem 4: Simplify \(16^{3/4}\)
Solution:
- Rewrite 16 as a power of 2: \(16 = 2^4\)
- Apply the rational exponent: \(16^{3/4} = (2^4)^{3/4}\)
- Use the power rule: \((a^m)^n = a^{mn}\): \((2^4)^{3/4} = 2^{4 \times (3/4)} = 2^3\)
- Simplify: \(2^3 = 8\)
-
Problem 5: Simplify \(\left(\frac{27}{8}\right)^{2/3}\)
Solution:
- Separate the fraction: \(\left(\frac{27}{8}\right)^{2/3} = \frac{27^{2/3}}{8^{2/3}}\)
- Rewrite 27 and 8 as powers of 3 and 2 respectively: \(27 = 3^3\), \(8 = 2^3\)
- Apply the rational exponents: \(\frac{(3^3)^{2/3}}{(2^3)^{2/3}} = \frac{3^{3 \cdot (2/3)}}{2^{3 \cdot (2/3)}}\)
- Simplify the exponents: \(\frac{3^2}{2^2} = \frac{9}{4}\)
Additional Resources for Mastery
Mastering the simplification of radical expressions and exponents can be greatly enhanced by utilizing various resources. Below are some recommended resources that offer in-depth explanations, practice problems, and interactive learning opportunities:
-
Khan Academy:
Khan Academy offers a comprehensive set of tutorials on rational exponents and radicals. Their platform includes instructional videos, practice exercises, and quizzes to test your understanding.
-
Mathematics LibreTexts:
The Mathematics LibreTexts library provides detailed explanations and examples on simplifying radical expressions, including the use of product and quotient rules for radicals. This resource is great for reviewing key concepts and practicing problem-solving skills.
-
Interactive Algebra:
This site offers interactive lessons and practice problems for simplifying radical expressions. It is a helpful tool for visual learners who benefit from interactive content.
-
Wolfram Alpha:
Wolfram Alpha is a powerful computational engine that can help you solve and verify solutions to problems involving radical expressions and exponents. You can use it to check your work and explore different problem-solving approaches.
-
Purplemath:
Purplemath offers practical advice and detailed explanations on a variety of algebra topics, including rational exponents and radical expressions. Their resources are useful for both learning new concepts and reviewing previously covered material.
By exploring these resources, you can deepen your understanding and achieve mastery in simplifying radical expressions and exponents. Happy learning!
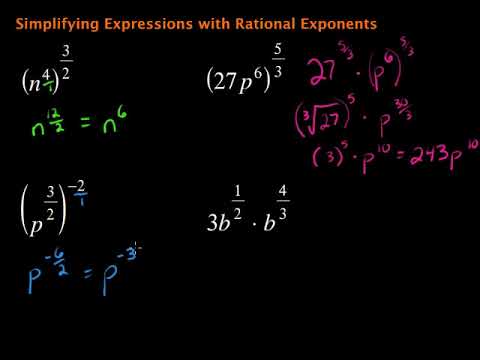
Hướng dẫn đơn giản hóa biểu thức căn bậc với các biến để thu hút người xem.
Đơn Giản Hóa Biểu Thức Căn Bậc Với Biến
READ MORE:
Video hướng dẫn chi tiết về cách đơn giản hóa các biểu thức với số mũ hữu tỉ.
Đơn Giản Hóa Biểu Thức Với Số Mũ Hữu Tỉ