Topic simplifying radical expressions multiplying: Welcome to our comprehensive guide on simplifying radical expressions, focusing on mastering multiplication techniques. This article will help you understand the basics, apply the product rule, and avoid common mistakes while multiplying radicals. Get ready to enhance your skills with step-by-step examples and advanced techniques.
Table of Content
- Simplifying Radical Expressions by Multiplying
- Introduction to Radical Expressions
- Basics of Multiplying Radicals
- Understanding the Product Rule
- Simplifying Radicals Before Multiplication
- Step-by-Step Examples of Multiplication
- Distributive Property with Radicals
- Special Cases and Conjugates
- Common Mistakes to Avoid
- Practice Problems
- Advanced Techniques and Applications
- Conclusion and Further Reading
- YOUTUBE: Xem video: Nhân Các Biểu Thức Đa Thức Với Biến Số Và Số Mũ trong các biểu thức căn bậc hai.
Simplifying Radical Expressions by Multiplying
Multiplying radical expressions involves combining the radicands under a single radical when possible. The product of two radicals is equivalent to the radical of the product. This method simplifies the expression, making it more manageable.
Basic Steps for Multiplication
- Multiply the coefficients (if any).
- Multiply the radicands together under a single radical.
- Simplify the resulting radical if possible.
Example: Multiplying Simple Radicals
Consider the expression \( \sqrt{3} \times \sqrt{12} \):
- Combine the radicands: \( \sqrt{3 \times 12} = \sqrt{36} \).
- Simplify the radical: \( \sqrt{36} = 6 \).
Multiplying Binomials with Radicals
When multiplying binomials containing radicals, use the FOIL method (First, Outer, Inner, Last) to expand the expression.
Example: FOIL Method
Multiply \( (2 + \sqrt{3})(1 - \sqrt{3}) \):
- First: \( 2 \times 1 = 2 \).
- Outer: \( 2 \times -\sqrt{3} = -2\sqrt{3} \).
- Inner: \( \sqrt{3} \times 1 = \sqrt{3} \).
- Last: \( \sqrt{3} \times -\sqrt{3} = -3 \).
Combine like terms: \( 2 - 3 - 2\sqrt{3} + \sqrt{3} = -1 - \sqrt{3} \).
Multiplying Conjugates
Conjugates are pairs of binomials of the form \( (a + \sqrt{b})(a - \sqrt{b}) \). Multiplying conjugates results in a difference of squares, eliminating the radicals:
- Example: \( (\sqrt{5} + 1)(\sqrt{5} - 1) = 5 - 1 = 4 \).
Conclusion
Understanding how to multiply radicals simplifies many algebraic expressions. Practice using the distributive property and the FOIL method to master multiplying radical expressions.

READ MORE:
Introduction to Radical Expressions
Radical expressions involve roots, such as square roots, cube roots, and higher-order roots. Understanding these expressions is crucial for simplifying and manipulating them in mathematical equations. In this section, we'll explore the basics of radical expressions, their components, and foundational concepts to help you become proficient in working with them.
- Radical Sign: The symbol \( \sqrt{} \) represents the radical sign, indicating the root operation.
- Radicand: The number or expression inside the radical sign, which we aim to find the root of.
- Index: The small number outside and to the left of the radical sign, indicating the degree of the root. For square roots, the index is 2 (often omitted).
To work with radical expressions, it's important to understand their properties and rules, which will be covered in the following sections. Mastering these basics will provide a strong foundation for more advanced topics such as multiplying and simplifying radicals.
Here are some key points to keep in mind:
- Radicals can be simplified by factoring out perfect squares (or cubes, etc.) from the radicand.
- Multiplication of radicals follows specific rules that we'll explore in depth.
- Understanding the properties of radicals is essential for solving equations and simplifying expressions effectively.
Basics of Multiplying Radicals
Multiplying radicals involves a few simple rules and steps. The primary principle is the product rule for radicals, which states that the product of two radicals is the same as the radical of the product. This means:
\[
\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}
\]
Here's a detailed guide to multiplying radicals:
- Multiply the coefficients: If there are numbers outside the radicals (coefficients), multiply them together first.
- Multiply the radicands: Multiply the numbers inside the radicals (radicands) together.
- Simplify the resulting radical: If possible, simplify the new radicand by factoring out perfect squares.
Let's go through some examples to illustrate these steps:
Example 1
Multiply \(2 \sqrt{3} \cdot 5 \sqrt{2}\):
- Multiply the coefficients: \(2 \cdot 5 = 10\).
- Multiply the radicands: \(\sqrt{3} \cdot \sqrt{2} = \sqrt{6}\).
- Combine the results: \(10 \sqrt{6}\).
So, \(2 \sqrt{3} \cdot 5 \sqrt{2} = 10 \sqrt{6}\).
Example 2
Multiply \(\sqrt{8} \cdot \sqrt{2}\):
- Multiply the radicands: \(\sqrt{8} \cdot \sqrt{2} = \sqrt{16}\).
- Simplify the resulting radical: \(\sqrt{16} = 4\).
So, \(\sqrt{8} \cdot \sqrt{2} = 4\).
Example 3
Multiply \(\sqrt{3} \cdot \sqrt{12}\):
- Multiply the radicands: \(\sqrt{3} \cdot \sqrt{12} = \sqrt{36}\).
- Simplify the resulting radical: \(\sqrt{36} = 6\).
So, \(\sqrt{3} \cdot \sqrt{12} = 6\).
Example 4
Multiply \(\sqrt{5} \cdot \sqrt{10}\):
- Multiply the radicands: \(\sqrt{5} \cdot \sqrt{10} = \sqrt{50}\).
- Simplify the resulting radical: \(\sqrt{50} = \sqrt{25 \cdot 2} = 5 \sqrt{2}\).
So, \(\sqrt{5} \cdot \sqrt{10} = 5 \sqrt{2}\).
Special Case: Multiplying Conjugates
When multiplying conjugate radical expressions, the middle terms cancel out, and the product is a rational number. For example:
Multiply \((\sqrt{a} + \sqrt{b})(\sqrt{a} - \sqrt{b})\):
Using the distributive property (FOIL method):
- \((\sqrt{a})(\sqrt{a}) = a\)
- \((\sqrt{a})(-\sqrt{b}) = -\sqrt{ab}\)
- \((\sqrt{b})(\sqrt{a}) = \sqrt{ab}\)
- \((\sqrt{b})(-\sqrt{b}) = -b\)
Combine the results: \(a - b\).
So, \((\sqrt{a} + \sqrt{b})(\sqrt{a} - \sqrt{b}) = a - b\).
By following these steps and practicing with various examples, you can master the basics of multiplying radicals.
Understanding the Product Rule
The Product Rule for radicals is a fundamental concept that simplifies the multiplication of radical expressions. According to the Product Rule, the product of two radicals is equal to the radical of the product of their radicands. Mathematically, this can be expressed as:
\[
\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}
\]
This rule can be generalized to any root, not just square roots:
\[
\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{a \cdot b}
\]
Understanding and applying the Product Rule allows for the simplification of more complex radical expressions. Below, we will explore the Product Rule in detail with step-by-step examples.
Example 1: Multiplying Simple Radicals
Consider the multiplication of two simple radicals:
\[
\sqrt{3} \cdot \sqrt{12}
\]
Using the Product Rule, we multiply the radicands (3 and 12) together:
\[
\sqrt{3 \cdot 12} = \sqrt{36}
\]
Since 36 is a perfect square, we can simplify further:
\[
\sqrt{36} = 6
\]
Thus, \(\sqrt{3} \cdot \sqrt{12} = 6\).
Example 2: Multiplying Radicals with Variables
Next, let's multiply radicals that include variables:
\[
\sqrt{2x} \cdot \sqrt{5y}
\]
Using the Product Rule, we combine the radicands under one radical sign:
\[
\sqrt{2x \cdot 5y} = \sqrt{10xy}
\]
There are no further simplifications, so the final answer is \(\sqrt{10xy}\).
Example 3: Higher-Order Radicals
The Product Rule also applies to higher-order roots. Consider the following cube roots:
\[
\sqrt[3]{4} \cdot \sqrt[3]{9}
\]
Using the Product Rule for cube roots, we have:
\[
\sqrt[3]{4 \cdot 9} = \sqrt[3]{36}
\]
Thus, \(\sqrt[3]{4} \cdot \sqrt[3]{9} = \sqrt[3]{36}\).
Important Considerations
- The radicands must be non-negative when dealing with real numbers.
- The roots must be of the same order (e.g., both square roots, both cube roots) for the Product Rule to apply directly.
Practice Problems
- Simplify \(\sqrt{7} \cdot \sqrt{14}\).
- Simplify \(\sqrt[4]{2} \cdot \sqrt[4]{8}\).
- Simplify \(\sqrt{3a} \cdot \sqrt{6b}\).
By practicing these problems, you will become more comfortable with using the Product Rule to simplify radical expressions.
Simplifying Radicals Before Multiplication
Before multiplying radical expressions, it is often easier to simplify the radicals first. This helps to avoid dealing with large and complex numbers. Follow these steps to simplify radicals before multiplying:
- Identify and factor the radicand into its prime factors.
- Look for perfect squares (for square roots), perfect cubes (for cube roots), or higher powers that match the root index.
- Rewrite the radical expression, pulling out the perfect powers.
Consider the following example:
Simplify \(\sqrt{72} \cdot \sqrt{18}\) before multiplying.
- Factor each radicand:
- \(\sqrt{72} = \sqrt{2^3 \cdot 3^2} = \sqrt{2^2 \cdot 2 \cdot 3^2} = 6\sqrt{2}\)
- \(\sqrt{18} = \sqrt{2 \cdot 3^2} = 3\sqrt{2}\)
- Rewrite the expression using the simplified radicals:
\(6\sqrt{2} \cdot 3\sqrt{2}\)
- Multiply the coefficients and the radicals:
\( (6 \cdot 3) \cdot (\sqrt{2} \cdot \sqrt{2}) = 18 \cdot 2 = 36 \)
Thus, \(\sqrt{72} \cdot \sqrt{18} = 36\).
Another example involves cube roots:
Simplify \(\sqrt[3]{54} \cdot \sqrt[3]{16}\) before multiplying.
- Factor each radicand:
- \(\sqrt[3]{54} = \sqrt[3]{2 \cdot 3^3} = 3\sqrt[3]{2}\)
- \(\sqrt[3]{16} = \sqrt[3]{2^4} = 2\sqrt[3]{2}\)
- Rewrite the expression using the simplified radicals:
\(3\sqrt[3]{2} \cdot 2\sqrt[3]{2}\)
- Multiply the coefficients and the radicals:
\( (3 \cdot 2) \cdot (\sqrt[3]{2} \cdot \sqrt[3]{2}) = 6 \cdot \sqrt[3]{4} \)
Thus, \(\sqrt[3]{54} \cdot \sqrt[3]{16} = 6\sqrt[3]{4}\).
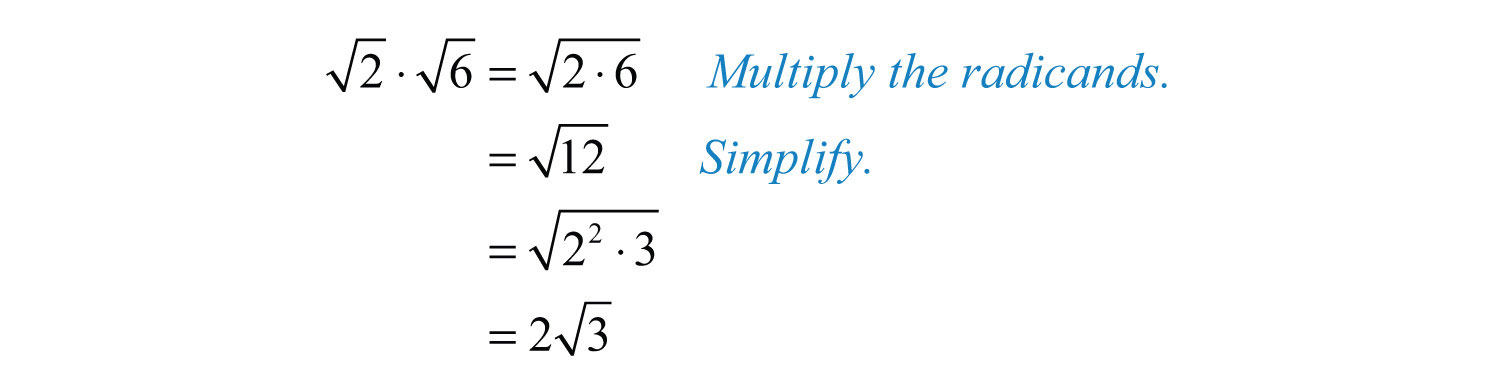
Step-by-Step Examples of Multiplication
To understand how to multiply radical expressions, let's look at several examples and simplify them step-by-step. These examples will help illustrate the process clearly.
Example 1: Multiplying Simple Radicals
Consider the expression \( \sqrt{3} \times \sqrt{12} \).
- Multiply the radicands (the numbers inside the radicals):
\[ \sqrt{3} \times \sqrt{12} = \sqrt{3 \times 12} = \sqrt{36} \] - Simplify the result:
\[ \sqrt{36} = 6 \]
Example 2: Multiplying Radicals with Different Coefficients
Consider the expression \( 2\sqrt{5} \times 3\sqrt{10} \).
- Multiply the coefficients (numbers outside the radicals):
\[ 2 \times 3 = 6 \] - Multiply the radicands:
\[ \sqrt{5} \times \sqrt{10} = \sqrt{50} \] - Combine the results:
\[ 2\sqrt{5} \times 3\sqrt{10} = 6\sqrt{50} \] - Simplify the radical if possible:
\[ 6\sqrt{50} = 6\sqrt{25 \times 2} = 6 \times 5\sqrt{2} = 30\sqrt{2} \]
Example 3: Multiplying Binomials with Radicals
Consider the expression \( (\sqrt{2} + \sqrt{3})(\sqrt{5} + \sqrt{7}) \).
- Use the distributive property to expand the expression:
\[ (\sqrt{2} + \sqrt{3})(\sqrt{5} + \sqrt{7}) = \sqrt{2}\sqrt{5} + \sqrt{2}\sqrt{7} + \sqrt{3}\sqrt{5} + \sqrt{3}\sqrt{7} \] - Multiply the radicands:
\[ \sqrt{2}\sqrt{5} = \sqrt{10}, \quad \sqrt{2}\sqrt{7} = \sqrt{14}, \quad \sqrt{3}\sqrt{5} = \sqrt{15}, \quad \sqrt{3}\sqrt{7} = \sqrt{21} \] - Combine all terms:
\[ \sqrt{10} + \sqrt{14} + \sqrt{15} + \sqrt{21} \]
Example 4: Multiplying Radicals with Variables
Consider the expression \( \sqrt{6x} \times 5\sqrt{6x} \).
- Multiply the coefficients:
\[ 5 \times 1 = 5 \] - Multiply the radicands:
\[ \sqrt{6x} \times \sqrt{6x} = \sqrt{(6x)(6x)} = \sqrt{36x^2} \] - Simplify the result:
\[ \sqrt{36x^2} = 6x \] - Combine the results:
\[ 5\sqrt{6x} \times \sqrt{6x} = 5 \times 6x = 30x \]
Example 5: Multiplying Negative Radicals
Consider the expression \( -7\sqrt{2} \times 7\sqrt{3} \).
- Multiply the coefficients:
\[ -7 \times 7 = -49 \] - Multiply the radicands:
\[ \sqrt{2} \times \sqrt{3} = \sqrt{6} \] - Combine the results:
\[ -7\sqrt{2} \times 7\sqrt{3} = -49\sqrt{6} \]
Practice Problems
- \( \sqrt{2} \times \sqrt{6} \)
- \( \sqrt{5} \times \sqrt{8} \)
- \( \sqrt{8} \times 3\sqrt{3} \)
- \( 3\sqrt{7} \times 6\sqrt{2} \)
- \( \sqrt{6x} \times 5\sqrt{6x} \)
- \( -7\sqrt{2} \times 7\sqrt{3} \)
Use the steps shown in the examples to solve these practice problems.
Distributive Property with Radicals
The distributive property is a useful tool when working with radical expressions. It allows us to multiply a single term by each term within a parenthesis, and it can be applied in various scenarios involving radicals. Here are some steps and examples to understand how to use the distributive property with radicals effectively.
Consider the expression \( a(b + c) \). According to the distributive property, this can be expanded as:
\[ a(b + c) = ab + ac \]
When dealing with radicals, the principle remains the same. Let's go through a few examples to illustrate this:
Example 1
Multiply \( \sqrt{3}(\sqrt{2} + \sqrt{5}) \):
- Distribute \( \sqrt{3} \) to each term inside the parenthesis:
- \[ \sqrt{3} \cdot \sqrt{2} + \sqrt{3} \cdot \sqrt{5} \]
- Use the product rule for radicals to simplify each term:
- \[ \sqrt{6} + \sqrt{15} \]
So, \( \sqrt{3}(\sqrt{2} + \sqrt{5}) = \sqrt{6} + \sqrt{15} \).
Example 2
Multiply \( 2\sqrt{5}(3\sqrt{2} - \sqrt{3}) \):
- Distribute \( 2\sqrt{5} \) to each term inside the parenthesis:
- \[ 2\sqrt{5} \cdot 3\sqrt{2} - 2\sqrt{5} \cdot \sqrt{3} \]
- Multiply the coefficients and then the radicals:
- \[ 6\sqrt{10} - 2\sqrt{15} \]
So, \( 2\sqrt{5}(3\sqrt{2} - \sqrt{3}) = 6\sqrt{10} - 2\sqrt{15} \).
Example 3
Multiply \( (\sqrt{7} + 2)(\sqrt{7} - 3) \) using the FOIL method:
- First: \( \sqrt{7} \cdot \sqrt{7} = 7 \)
- Outer: \( \sqrt{7} \cdot (-3) = -3\sqrt{7} \)
- Inner: \( 2 \cdot \sqrt{7} = 2\sqrt{7} \)
- Last: \( 2 \cdot (-3) = -6 \)
- Combine all terms:
- \[ 7 - 3\sqrt{7} + 2\sqrt{7} - 6 \]
- Simplify the expression:
- \[ 1 - \sqrt{7} \]
So, \( (\sqrt{7} + 2)(\sqrt{7} - 3) = 1 - \sqrt{7} \).
These examples demonstrate how the distributive property can be applied to radical expressions. By distributing and then simplifying, we can manage even complex radical multiplications systematically.
Special Cases and Conjugates
When working with radical expressions, special cases often arise that require the use of conjugates to simplify the expressions. Conjugates are particularly useful for rationalizing denominators containing radicals. The conjugate of an expression \(a + b\sqrt{c}\) is \(a - b\sqrt{c}\), and vice versa.
Here is a step-by-step guide on how to use conjugates in special cases:
-
Identify the Conjugate: For any binomial expression \(a + b\sqrt{c}\), its conjugate is \(a - b\sqrt{c}\).
-
Multiply by the Conjugate: Multiply both the numerator and the denominator by the conjugate of the denominator.
Example:
Simplify \(\frac{1}{2 - \sqrt{3}}\):
- Identify the conjugate of \(2 - \sqrt{3}\), which is \(2 + \sqrt{3}\).
- Multiply both numerator and denominator by \(2 + \sqrt{3}\):
\[
\frac{1}{2 - \sqrt{3}} \times \frac{2 + \sqrt{3}}{2 + \sqrt{3}} = \frac{2 + \sqrt{3}}{(2 - \sqrt{3})(2 + \sqrt{3})}
\] -
Apply the Difference of Squares Formula: Use the formula \((a - b)(a + b) = a^2 - b^2\) to simplify the denominator.
Example:
- Apply the formula to the denominator:
- The expression simplifies to:
\[
(2 - \sqrt{3})(2 + \sqrt{3}) = 2^2 - (\sqrt{3})^2 = 4 - 3 = 1
\]
\[
\frac{2 + \sqrt{3}}{1} = 2 + \sqrt{3}
\]
Let's look at another example where we have a more complex radical expression:
Simplify \(\frac{3}{5 - 2\sqrt{7}}\):
- Identify the conjugate of \(5 - 2\sqrt{7}\), which is \(5 + 2\sqrt{7}\).
- Multiply both numerator and denominator by \(5 + 2\sqrt{7}\):
- Apply the difference of squares formula to the denominator:
- The expression simplifies to:
\[
\frac{3}{5 - 2\sqrt{7}} \times \frac{5 + 2\sqrt{7}}{5 + 2\sqrt{7}} = \frac{3(5 + 2\sqrt{7})}{(5 - 2\sqrt{7})(5 + 2\sqrt{7})}
\]
\[
(5 - 2\sqrt{7})(5 + 2\sqrt{7}) = 5^2 - (2\sqrt{7})^2 = 25 - 4 \cdot 7 = 25 - 28 = -3
\]
\[
\frac{3(5 + 2\sqrt{7})}{-3} = \frac{15 + 6\sqrt{7}}{-3} = -5 - 2\sqrt{7}
\]
In summary, using conjugates to simplify radical expressions involves identifying the conjugate of the denominator, multiplying both the numerator and denominator by this conjugate, and then applying the difference of squares formula to simplify the expression.
Common Mistakes to Avoid
When simplifying and multiplying radical expressions, it's easy to make errors that can lead to incorrect results. Here are some common mistakes and tips on how to avoid them:
- Not Simplifying Radicals Fully:
Always simplify radicals before performing operations. For example, simplify \(\sqrt{50}\) to \(5\sqrt{2}\) before multiplying.
- Incorrect Use of the Product Rule:
Ensure you correctly apply the product rule: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}\). For instance, \(\sqrt{3} \cdot \sqrt{12} = \sqrt{36} = 6\).
- Ignoring the Distributive Property:
When multiplying binomials with radicals, apply the distributive property accurately. For example:
\[
(\sqrt{3} + 2)(\sqrt{3} - 1) = \sqrt{3} \cdot \sqrt{3} - \sqrt{3} + 2\sqrt{3} - 2 = 3 + \sqrt{3} - 2
\] - Incorrectly Combining Radicals:
Radicals can only be combined if they have the same radicand. For example, \(2\sqrt{3} + 4\sqrt{3} = 6\sqrt{3}\), but \(2\sqrt{3} + 4\sqrt{2}\) cannot be simplified further.
- Misapplying the Quotient Rule:
When dividing radicals, use the quotient rule correctly: \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\). For example, \(\frac{\sqrt{8}}{\sqrt{2}} = \sqrt{4} = 2\).
- Forgetting to Rationalize Denominators:
Always rationalize denominators with radicals. Multiply the numerator and denominator by the conjugate if necessary. For example:
\[
\frac{5}{\sqrt{3}} = \frac{5 \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{5\sqrt{3}}{3}
\] - Not Simplifying Final Expressions:
After performing all operations, ensure the final expression is simplified completely. Combine like terms and simplify all radicals.
By being aware of these common pitfalls and carefully applying the rules for radicals, you can avoid mistakes and accurately simplify and multiply radical expressions.

Practice Problems
Practice makes perfect! Here are some practice problems to help you master multiplying and simplifying radical expressions. Try solving these problems step-by-step to ensure you understand the concepts.
-
Simplify the following expression:
\(\sqrt{12} \cdot \sqrt{3}\)
Solution:
- Use the product rule for radicals: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\)
- \(\sqrt{12} \cdot \sqrt{3} = \sqrt{12 \cdot 3} = \sqrt{36}\)
- Simplify the radical: \(\sqrt{36} = 6\)
-
Multiply and simplify:
\(\sqrt{8} \cdot \sqrt{2}\)
Solution:
- Apply the product rule: \(\sqrt{8} \cdot \sqrt{2} = \sqrt{8 \cdot 2} = \sqrt{16}\)
- Simplify the radical: \(\sqrt{16} = 4\)
-
Simplify the expression:
\(\sqrt{50} \cdot \sqrt{2}\)
Solution:
- Use the product rule: \(\sqrt{50} \cdot \sqrt{2} = \sqrt{50 \cdot 2} = \sqrt{100}\)
- Simplify the radical: \(\sqrt{100} = 10\)
-
Multiply and simplify:
\(2\sqrt{3} \cdot 4\sqrt{6}\)
Solution:
- Multiply the coefficients: \(2 \cdot 4 = 8\)
- Multiply the radicals: \(\sqrt{3} \cdot \sqrt{6} = \sqrt{18}\)
- Combine the results: \(8\sqrt{18}\)
- Simplify the radical: \(8 \cdot \sqrt{9 \cdot 2} = 8 \cdot 3\sqrt{2} = 24\sqrt{2}\)
-
Simplify the product:
\(\sqrt{27} \cdot \sqrt{3}\)
Solution:
- Apply the product rule: \(\sqrt{27} \cdot \sqrt{3} = \sqrt{81}\)
- Simplify the radical: \(\sqrt{81} = 9\)
Advanced Techniques and Applications
When dealing with multiplying radical expressions, advanced techniques can help in various scenarios:
- Rationalizing Denominators: This technique involves eliminating radicals from the denominator of a fraction, often by multiplying by a cleverly chosen form of 1. For example, to rationalize \( \frac{1}{\sqrt{2}} \), multiply numerator and denominator by \( \sqrt{2} \).
- Handling Higher Index Radicals: Radicals with indexes higher than 2 require special handling. For instance, \( \sqrt[3]{a} \cdot \sqrt[3]{b} = \sqrt[3]{ab} \).
- Combining Radicals: When multiplying expressions with radicals, simplify by combining like terms under the same radical sign. For example, \( \sqrt{2} \cdot \sqrt{3} = \sqrt{6} \).
- Complex Numbers: Radicals can involve complex numbers, where operations like conjugation and absolute value play a crucial role in simplification.
- Applications in Geometry: Radical expressions frequently appear in geometric problems, such as calculating distances in coordinate geometry or areas of figures with radical dimensions.
- Graphing and Equations: Understanding how radical expressions behave graphically and their implications in solving equations can provide deeper insights into their manipulation and simplification.
Conclusion and Further Reading
Mastering the art of multiplying radical expressions opens doors to deeper mathematical understanding and problem-solving skills. By following the principles discussed in this guide, you can confidently simplify and manipulate radical expressions in various contexts.
For further exploration:
- Continue practicing with a variety of problems to reinforce your skills.
- Explore advanced textbooks and online resources dedicated to algebra and precalculus.
- Engage in interactive tutorials and videos to enhance your understanding of radical operations.
- Consider exploring applications of radicals in fields such as physics, engineering, and computer science.
Xem video: Nhân Các Biểu Thức Đa Thức Với Biến Số Và Số Mũ trong các biểu thức căn bậc hai.
Multiplying Radical Expressions With Variables and Exponents | Video
READ MORE:
Xem video: Nhân Các Căn Bậc Hai và Sau Đó Đơn Giản Hóa chúng trong các biểu thức căn bậc hai.
Multiplying Radicals and Then Simplifying | Video