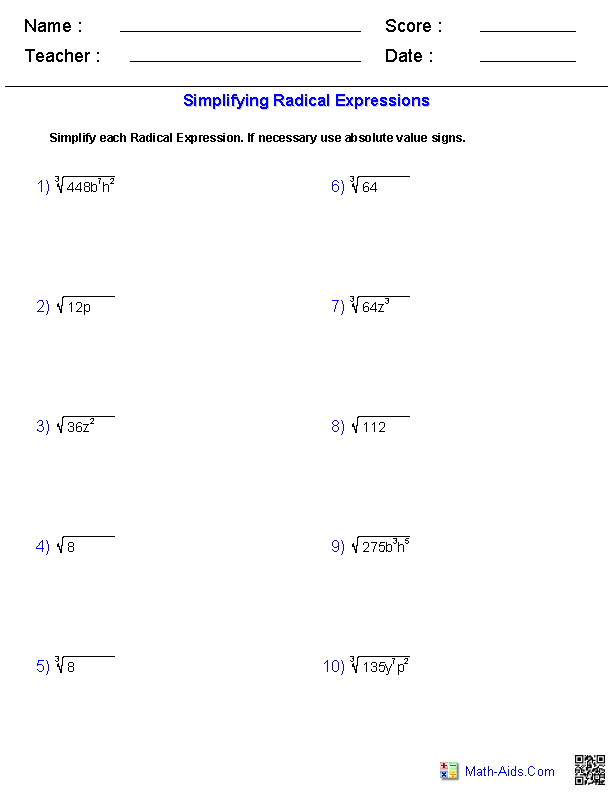Topic simplifying radical expressions khan academy: Discover how to master simplifying radical expressions with Khan Academy. This comprehensive guide provides step-by-step instructions and insights, making it easy to understand and apply. Whether you're a student or a lifelong learner, this article will help you confidently tackle radical expressions and enhance your math skills.
Table of Content
- Simplifying Radical Expressions
- Understanding Radicals and Roots
- Properties of Square Roots
- How to Simplify Square Roots
- Simplifying Radicals with Variables
- Simplifying Higher Roots
- Adding and Subtracting Radical Expressions
- Multiplying and Dividing Radical Expressions
- Rationalizing the Denominator
- Special Cases in Radical Simplification
- Practice Problems and Solutions
- Common Mistakes and How to Avoid Them
- YOUTUBE:
Simplifying Radical Expressions
Understanding how to simplify radical expressions is essential for mastering algebra and higher-level mathematics. Simplifying radicals involves expressing the radical in its simplest form by removing any perfect square factors. Let's explore this step-by-step.
What is a Radical Expression?
A radical expression includes a square root, cube root, or any higher-order root. The most common radical expression is the square root. For example, \( \sqrt{50} \) is a radical expression.
Steps to Simplify Radical Expressions
- Identify the prime factors of the number under the radical.
- Group the factors into pairs for square roots, triples for cube roots, etc.
- Move each pair or group of factors outside the radical.
- Multiply the factors outside the radical.
- Write the simplified radical expression.
Example: Simplifying \( \sqrt{72} \)
Let's simplify \( \sqrt{72} \) step-by-step:
- Find the prime factors of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Group the factors into pairs: \( (2 \times 2) \) and \( (3 \times 3) \)
- Move each pair outside the radical: \( 2 \) and \( 3 \)
- Multiply the factors outside the radical: \( 2 \times 3 = 6 \)
- Write the simplified expression: \( \sqrt{72} = 6\sqrt{2} \)
Working with Variables
When simplifying radical expressions with variables, apply the same principles. For example, let's simplify \( \sqrt{50x^4y^2} \):
- Prime factors of 50: \( 50 = 2 \times 5 \times 5 \)
- Variables: \( x^4 = x^2 \times x^2 \) and \( y^2 = y \times y \)
- Group the factors: \( (5 \times 5) \), \( (x^2 \times x^2) \), and \( (y \times y) \)
- Move each pair outside the radical: \( 5 \), \( x^2 \), and \( y \)
- Write the simplified expression: \( \sqrt{50x^4y^2} = 5x^2y\sqrt{2} \)
Practice Problems
Try simplifying these radical expressions:
- \( \sqrt{18} \)
- \( \sqrt{32} \)
- \( \sqrt{45x^2} \)
- \( \sqrt{72y^3} \)
Conclusion
By following these steps and practicing regularly, you'll become proficient in simplifying radical expressions. Keep practicing, and remember that understanding the fundamentals is the key to success in mathematics!
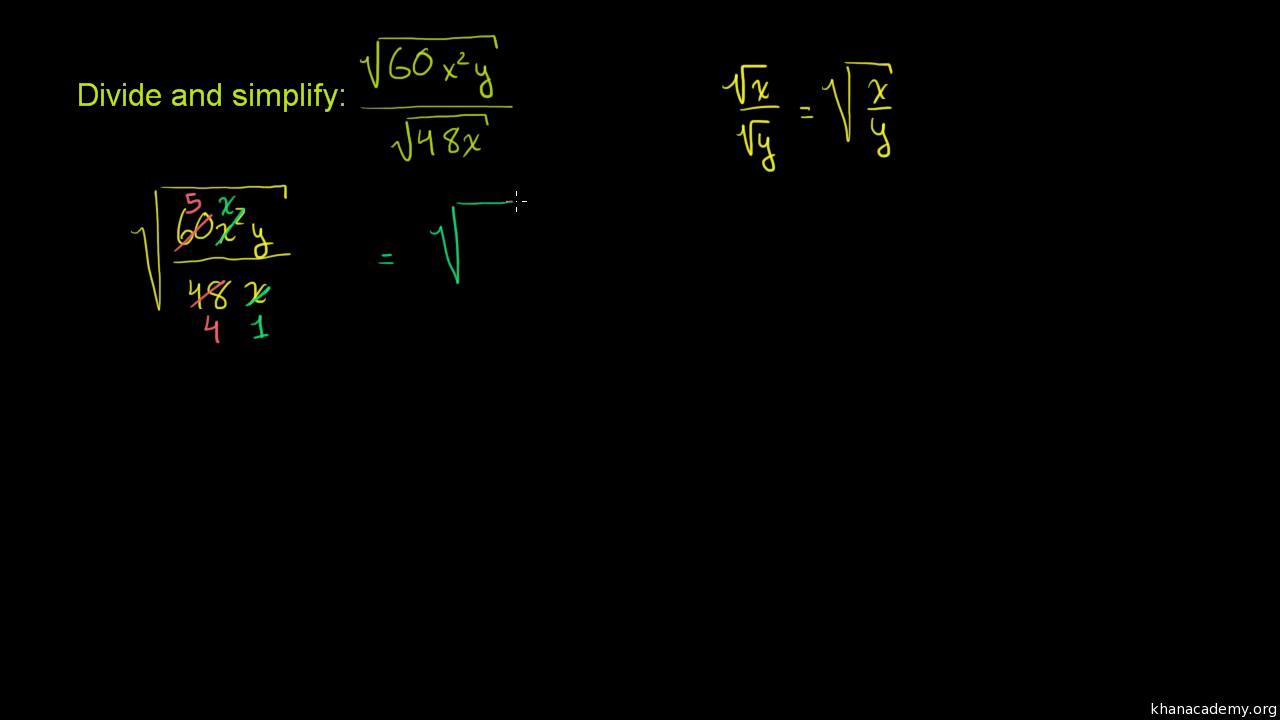
READ MORE:
Understanding Radicals and Roots
Radicals and roots are fundamental concepts in algebra, helping to simplify expressions and solve equations. A radical expression includes a root symbol (√) with an index indicating the degree of the root. The most common root is the square root, where the index is 2, but there are also cube roots (index 3) and higher.
For example, the square root of 16 is written as \( \sqrt{16} \), which equals 4, since \( 4^2 = 16 \).
-
Square Roots: The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). Mathematically, \( \sqrt{x} \) means \( y \) such that \( y^2 = x \).
- \( \sqrt{25} = 5 \) because \( 5^2 = 25 \)
- \( \sqrt{9} = 3 \) because \( 3^2 = 9 \)
-
Cube Roots: The cube root of a number \( x \) is a value that, when used three times in a multiplication, gives \( x \). Represented as \( \sqrt[3]{x} \).
- \( \sqrt[3]{27} = 3 \) because \( 3^3 = 27 \)
- \( \sqrt[3]{8} = 2 \) because \( 2^3 = 8 \)
Radicals can also be expressed using fractional exponents:
- \( x^{1/2} = \sqrt{x} \)
- \( x^{1/3} = \sqrt[3]{x} \)
Here’s a table summarizing some common roots:
| Expression | Radical Form | Result |
|---|---|---|
| Square Root of 36 | \( \sqrt{36} \) | 6 |
| Cube Root of 64 | \( \sqrt[3]{64} \) | 4 |
| Fourth Root of 81 | \( \sqrt[4]{81} \) | 3 |
Understanding how to simplify radical expressions is crucial in algebra. It involves rewriting them in their simplest form, combining like terms, and ensuring no radicals appear in the denominator of a fraction.
Properties of Square Roots
The properties of square roots help simplify and manipulate expressions involving radicals. Understanding these properties is essential for solving algebraic equations effectively.
- Product Property: For any non-negative numbers \(a\) and \(b\), the square root of a product is the product of the square roots: \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \]
- Quotient Property: For any non-negative numbers \(a\) and \(b\) (where \(b \neq 0\)), the square root of a quotient is the quotient of the square roots: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
- Power of a Square Root: The square root of a number raised to an even power is the number raised to half that power: \[ \sqrt{a^n} = a^{\frac{n}{2}} \] (for \(n\) even).
These properties can be used to simplify complex radical expressions. Here are examples:
- Simplify \( \sqrt{50} \): \[ \sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2} \]
- Simplify \( \sqrt{\frac{9}{16}} \): \[ \sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4} \]
- Simplify \( \sqrt{x^4} \): \[ \sqrt{x^4} = x^{\frac{4}{2}} = x^2 \]
Understanding these properties allows you to tackle more complex problems in algebra, providing a strong foundation for further mathematical learning.
How to Simplify Square Roots
Simplifying square roots involves finding the prime factors of the number under the square root and identifying perfect squares. Follow these steps:
- Identify the prime factors of the number. For example, to simplify √72, first find the prime factors: 72 = 2 × 2 × 2 × 3 × 3.
- Group the factors into pairs of the same number. In this case: (2 × 2) × (3 × 3) × 2.
- For each pair, take one factor out of the square root. This gives: 2 × 3 × √2.
- Multiply the factors outside the square root: 2 × 3 = 6.
- The simplified form is 6√2.
This method helps to simplify the square root by reducing it to its simplest radical form.
Simplifying Radicals with Variables
Simplifying radicals with variables involves a few steps to ensure the expression is in its simplest form:
- Identify perfect squares: Look for perfect square factors within the radicand (the expression inside the radical).
- Separate the variables: Break down the variables inside the radical into parts that can be simplified.
- Apply the square root to each part: Take the square root of both the numerical and variable parts separately.
- Combine the results: Multiply the simplified results together.
For example, to simplify √(50x4y3):
- Break down the numerical part: 50 = 25 × 2, and 25 is a perfect square.
- For variables, x4 is a perfect square (x2)2, and y3 can be written as y2y.
- Apply the square root: √(25x4y22y) = 5x2y√(2y).
The final simplified form is 5x2y√(2y).

Simplifying Higher Roots
Simplifying higher roots, such as cube roots or fourth roots, follows similar principles as simplifying square roots. Here are the steps to simplify higher roots:
- Identify the index of the root. For example, a cube root has an index of 3.
- Break down the number or expression inside the root into its prime factors or smaller expressions.
- Group the factors based on the index. For a cube root, group the factors into sets of three.
- Extract one factor from each group out of the root.
- Multiply the extracted factors together. The simplified form will have these factors outside the root, while any remaining factors stay inside.
For example, to simplify \( \sqrt[3]{27x^6} \):
- Prime factorize: \( 27 = 3^3 \) and \( x^6 = (x^2)^3 \).
- Group factors: \( (3^3)(x^2)^3 \).
- Extract from the root: \( 3x^2 \).
The simplified form is \( 3x^2 \).
This process helps in simplifying expressions involving higher roots and makes calculations easier.
Adding and Subtracting Radical Expressions
To add or subtract radicals, follow these steps:
- Ensure the radicals have the same index and radicand. For example, \(3\sqrt{2}\) and \(2\sqrt{2}\) are like radicals.
- Add or subtract the coefficients. For instance, \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\).
- If the radicals are not alike, they cannot be combined. For example, \(\sqrt{5}\) and \(\sqrt{2}\) remain separate.
Let's look at an example:
- \(2\sqrt{7} - 3\sqrt{7} = -\sqrt{7}\)
Remember, the radical part stays the same while you perform arithmetic on the coefficients.
Multiplying and Dividing Radical Expressions
To multiply and divide radical expressions, follow these steps:
-
Multiplying Radicals:
- Multiply the coefficients (numbers outside the radicals) together.
- Multiply the radicands (numbers inside the radicals) together.
- Simplify the resulting radical, if possible.
-
Dividing Radicals:
- Divide the coefficients and the radicands separately.
- If there is a radical in the denominator, rationalize it by multiplying the numerator and denominator by the conjugate.
- Simplify the expression.
Example:
Multiply \( \sqrt{3} \times \sqrt{12} = \sqrt{36} = 6 \).
Divide \( \frac{\sqrt{18}}{\sqrt{2}} = \sqrt{\frac{18}{2}} = \sqrt{9} = 3 \).
Rationalizing the Denominator
Rationalizing the denominator is a process used to eliminate radicals from the denominator of a fraction. Here's how to do it:
-
Identify the Radical:
- If the denominator contains a square root, multiply both the numerator and the denominator by that square root.
-
Multiply by the Conjugate:
- If the denominator is a binomial with a square root, multiply both the numerator and denominator by the conjugate. The conjugate is the same binomial with the opposite sign between the terms.
-
Simplify:
- Multiply out the expressions and simplify the result. The radical in the denominator should be eliminated, leaving a rational number.
Example:
To rationalize \(\frac{1}{\sqrt{2}}\), multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\) to get \(\frac{\sqrt{2}}{2}\).
For \(\frac{1}{3 + \sqrt{5}}\), multiply by \(\frac{3 - \sqrt{5}}{3 - \sqrt{5}}\) to rationalize the denominator.
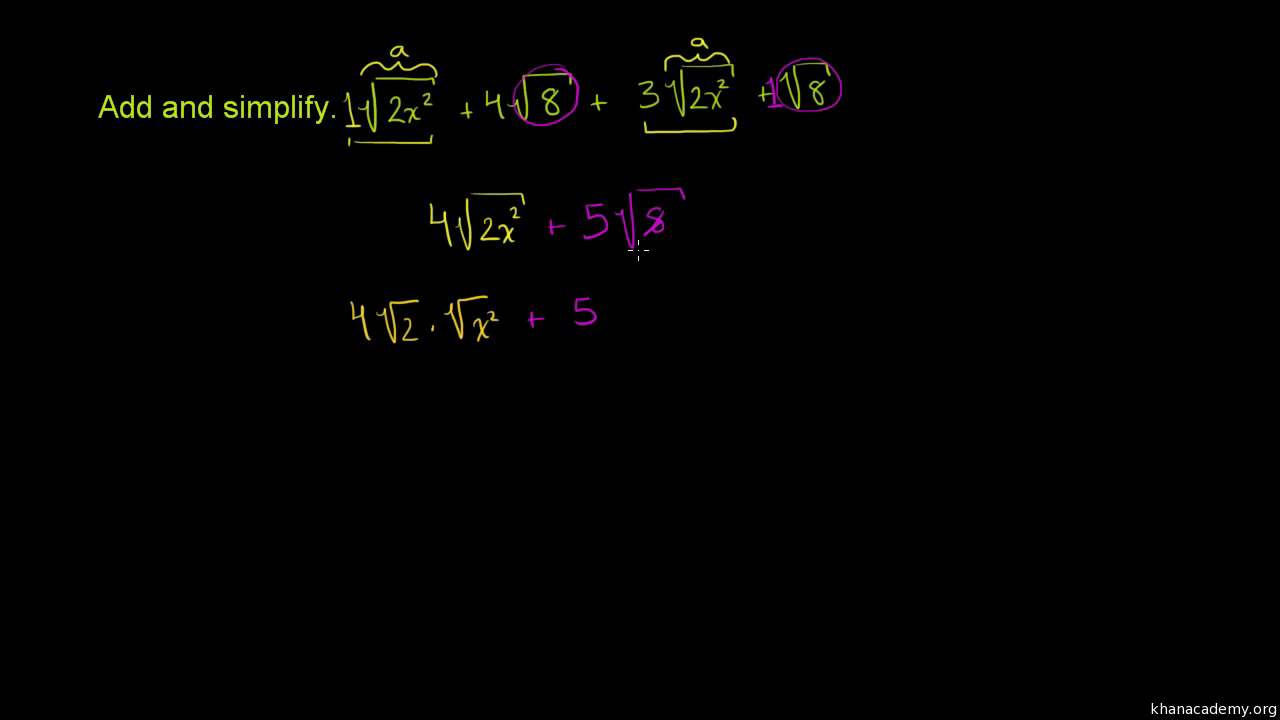
Special Cases in Radical Simplification
When simplifying radicals, there are unique scenarios that require special attention. Here are a few:
- Perfect Squares: If the radicand is a perfect square, the radical simplifies to an integer. For example, \(\sqrt{36} = 6\).
- Zero in the Radicand: Any radical with zero simplifies to zero, such as \(\sqrt{0} = 0\).
- Negative Radicand (in even roots): These do not have real solutions, for example, \(\sqrt{-4}\) is not a real number.
- Radicals in Denominators: Rationalizing the denominator is often required, such as simplifying \(\frac{1}{\sqrt{2}}\) to \(\frac{\sqrt{2}}{2}\).
- Combining Like Terms: Radicals can only be combined if they have the same radicand, such as \(\sqrt{2} + 3\sqrt{2} = 4\sqrt{2}\).
These special cases help streamline the process of simplifying radical expressions, ensuring the expressions are in their simplest form.
Practice Problems and Solutions
Practicing problems is essential for mastering the simplification of radical expressions. Below are a series of problems, each followed by detailed, step-by-step solutions.
Problem 1: Simplifying a Square Root
Simplify \( \sqrt{50} \).
- Factor 50 into its prime factors: \( 50 = 2 \times 5^2 \).
- Apply the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \): \( \sqrt{50} = \sqrt{2 \times 5^2} \).
- Simplify by taking the square root of the perfect square: \( \sqrt{2 \times 5^2} = \sqrt{2} \times 5 = 5\sqrt{2} \).
Problem 2: Simplifying a Radical with Variables
Simplify \( \sqrt{72x^3} \).
- Factor 72 into its prime factors: \( 72 = 2^3 \times 3^2 \).
- Combine the factors with the variable: \( \sqrt{72x^3} = \sqrt{2^3 \times 3^2 \times x^3} \).
- Simplify each part: \( \sqrt{2^3} = 2\sqrt{2} \), \( \sqrt{3^2} = 3 \), and \( \sqrt{x^3} = x\sqrt{x} \).
- Combine all parts: \( \sqrt{72x^3} = 3 \times 2 \times x \times \sqrt{2x} = 6x\sqrt{2x} \).
Problem 3: Adding Radical Expressions
Simplify \( 2\sqrt{18} + 3\sqrt{8} \).
- Simplify each radical: \( \sqrt{18} = 3\sqrt{2} \) and \( \sqrt{8} = 2\sqrt{2} \).
- Substitute back into the expression: \( 2(3\sqrt{2}) + 3(2\sqrt{2}) \).
- Multiply the coefficients: \( 6\sqrt{2} + 6\sqrt{2} \).
- Combine like terms: \( 12\sqrt{2} \).
Problem 4: Rationalizing the Denominator
Simplify \( \frac{5}{\sqrt{3}} \).
- Multiply the numerator and the denominator by \( \sqrt{3} \): \( \frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \).
- Simplify: \( \frac{5\sqrt{3}}{3} \).
Practice Table
| Problem | Solution |
|---|---|
| \(\sqrt{45}\) | \(3\sqrt{5}\) |
| \(\sqrt{27x^2}\) | \(3x\sqrt{3}\) |
| \(4\sqrt{12} + 3\sqrt{75}\) | \(14\sqrt{3}\) |
| \(\frac{7}{\sqrt{2}}\) | \(\frac{7\sqrt{2}}{2}\) |
For more practice, consider creating similar problems and solving them step-by-step. Consistent practice will help solidify your understanding and skills in simplifying radical expressions.
Common Mistakes and How to Avoid Them
When simplifying radical expressions, it's common to make errors that can lead to incorrect solutions. Here are some frequent mistakes and tips on how to avoid them:
- Incorrectly Combining Radicals:
Radicals can only be combined if they have the same index and radicand. For example,
- Misunderstanding the Distributive Property:
Apply the distributive property correctly:
Instead, use
- Forgetting to Simplify Completely:
Always check if the radical can be simplified further. For example,
- Ignoring Absolute Values:
When simplifying even roots of variables, remember to use absolute values if the variable could be negative. For example,
x^2 = |x|.
By being mindful of these common mistakes and understanding the correct procedures, you can simplify radical expressions accurately.
Đơn Giản Hoá Biểu Thức Căn Thức 1
READ MORE:
Video này hướng dẫn về cách thêm và đơn giản hóa các số căn bậc hai, rất phù hợp cho các bạn học sinh đang học toán sơ cấp.
Thêm và đơn giản hóa các số căn bậc hai | Toán học sơ cấp | Khan Academy