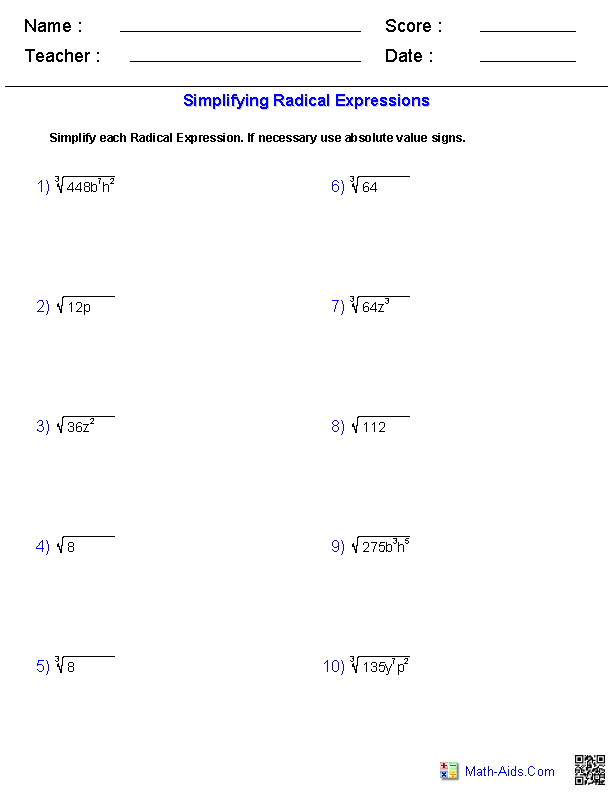Topic khan academy simplifying radical expressions: Discover how to simplify radical expressions with Khan Academy's expert guidance. This comprehensive guide covers everything from basic concepts to advanced techniques, ensuring you master the art of simplifying radicals with ease. Perfect for students and educators alike, enhance your math skills and boost your confidence in handling radical expressions.
Table of Content
- Simplifying Radical Expressions
- Understanding the Radical Symbol
- Prime Factorization Method
- Simplifying Square Roots
- Simplifying Cube Roots
- Simplifying Radicals with Variables
- Special Considerations in Simplifying Radicals
- Rationalizing the Denominator
- Combining Radical Expressions
- Examples and Practice Problems
- Common Mistakes to Avoid
- Advanced Techniques in Simplifying Radicals
- Applications of Simplifying Radical Expressions
- Additional Resources and References
- YOUTUBE: Hướng dẫn đơn giản hóa biểu thức căn bậc 2 với Khan Academy. Học cách làm chủ các biểu thức căn bậc 2 một cách dễ dàng và hiệu quả.
Simplifying Radical Expressions
Learning to simplify radical expressions is a crucial skill in algebra and higher mathematics. This process involves reducing the expression to its simplest form. The following content is inspired by resources from Khan Academy, which is known for its high-quality educational materials.
Introduction to Radical Expressions
A radical expression involves roots, such as square roots or cube roots. Simplifying these expressions makes them easier to work with in equations and other mathematical contexts.
Basic Steps to Simplify Radical Expressions
The process of simplifying radical expressions can generally be broken down into the following steps:
- Factor the number or expression under the radical into its prime factors.
- Group the factors into pairs (for square roots) or triples (for cube roots).
- Move each group of pairs or triples out from under the radical.
- Multiply the numbers outside the radical to get the simplified form.
Examples of Simplifying Radical Expressions
Here are some examples to illustrate the simplification process:
- \\(\sqrt{50} = \sqrt{2 \cdot 5 \cdot 5} = 5\sqrt{2}\\)
- \\(\sqrt{72} = \sqrt{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3} = 6\sqrt{2}\\)
- \\(\sqrt{18x^2} = \sqrt{2 \cdot 3 \cdot 3 \cdot x \cdot x} = 3x\sqrt{2}\\)
Special Considerations
When simplifying radical expressions, it is essential to keep the following in mind:
- Ensure all terms are fully simplified before concluding.
- Always look for opportunities to factor out perfect squares (for square roots) or higher powers.
- Check if the expression involves variables and handle them appropriately.
Practice Problems
To master simplifying radical expressions, practice is crucial. Try the following problems:
- Simplify \\(\sqrt{32}\\).
- Simplify \\(\sqrt{200}\\).
- Simplify \\(\sqrt{50x^4}\\).
Advanced Techniques
For those looking to deepen their understanding, consider these advanced techniques:
- Rationalizing the denominator of a radical expression.
- Simplifying radicals with higher roots, such as cube roots.
- Combining radical expressions using addition, subtraction, multiplication, and division.
Understanding and practicing these concepts will make working with radical expressions much more manageable and intuitive.
READ MORE:
Understanding the Radical Symbol
The radical symbol, often denoted as \( \sqrt{} \), is used in mathematics to indicate the square root of a number. It consists of the symbol \( \sqrt{} \) followed by the expression inside the radical, such as \( \sqrt{9} \). The number or expression inside the radical is known as the radicand.
Key points to understand about the radical symbol:
- It represents the principal (non-negative) square root of a number.
- For example, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
- If the radicand is negative, the square root is not a real number under the usual definition in the context of real numbers. In such cases, we use complex numbers or refer to the concept as not real.
- The radical symbol can extend beyond square roots to include cube roots (e.g., \( \sqrt[3]{27} = 3 \)) and higher roots, each indicated by the corresponding index outside the radical.
The radical symbol is essential in simplifying expressions involving roots and plays a crucial role in various mathematical operations and applications.
Prime Factorization Method
The prime factorization method is used to simplify radical expressions as follows:
- Find the prime factors of the radicand.
- Identify pairs of identical factors inside the radical.
- Bring each pair of factors outside the radical as a single factor.
- If there are remaining factors inside the radical that cannot form a pair, leave them inside.
- Simplify any remaining radicals if possible.
Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest form. To achieve this, you need to factorize the number under the square root and look for perfect square factors.
Step-by-Step Instructions
- Identify the number under the square root that you need to simplify. Let's denote this number as n.
- Find the prime factorization of n. This means expressing n as a product of its prime factors. For example, for \( n = 50 \): \[ 50 = 2 \times 5^2 \]
- Identify and group the pairs of prime factors. For instance, in \( 50 = 2 \times 5^2 \), we have one pair of \( 5 \).
- Take one factor out of each pair and place it outside the square root symbol. For the example \( \sqrt{50} \): \[ \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \]
- The simplified form of the square root is \( 5\sqrt{2} \).
Examples
- Example 1: Simplify \( \sqrt{72} \)
- Prime factorize 72: \( 72 = 2^3 \times 3^2 \)
- Group the pairs: \( (2^2 \times 3^2) \times 2 \)
- Simplify: \[ \sqrt{72} = \sqrt{2^2 \times 3^2 \times 2} = 2 \times 3 \sqrt{2} = 6\sqrt{2} \]
- Example 2: Simplify \( \sqrt{128} \)
- Prime factorize 128: \( 128 = 2^7 \)
- Group the pairs: \( (2^6) \times 2 = 2^3 \times 2 \times 2 \)
- Simplify: \[ \sqrt{128} = \sqrt{2^6 \times 2} = 2^3 \sqrt{2} = 8\sqrt{2} \]
Practice Problems
| Expression | Simplified Form |
|---|---|
| \( \sqrt{18} \) | \( 3\sqrt{2} \) |
| \( \sqrt{45} \) | \( 3\sqrt{5} \) |
| \( \sqrt{98} \) | \( 7\sqrt{2} \) |
By following these steps and practicing with different numbers, you can become proficient at simplifying square roots. Always remember to look for perfect square factors and group them outside the square root.
Simplifying Cube Roots
Simplifying cube roots follows a similar process to simplifying square roots but with a focus on identifying perfect cubes instead of perfect squares. Here are the detailed steps to simplify cube roots:
- Identify the Cube Root:
The cube root of a number \(a\) is written as \(\sqrt[3]{a}\) or \(a^{1/3}\). For example, \(\sqrt[3]{27}\) or \(27^{1/3}\).
- Prime Factorization:
Break down the number under the cube root into its prime factors. For instance, for \(\sqrt[3]{27}\), the prime factorization of 27 is \(3 \times 3 \times 3\).
- Group the Factors:
Group the prime factors into sets of three (since we are dealing with cube roots). For \(\sqrt[3]{27}\), we have \(3^3\).
- Extract the Cube Root:
For each group of three identical factors, take one factor out of the radical. In the case of \(\sqrt[3]{27}\), we take out one 3, resulting in \(3\).
- Write the Simplified Form:
The simplified form of \(\sqrt[3]{27}\) is 3. Thus, \(\sqrt[3]{27} = 3\).
Here is another example to illustrate the process:
Example: Simplify \(\sqrt[3]{64}\)
- Identify the Cube Root: \(\sqrt[3]{64}\)
- Prime Factorization: \(64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6\)
- Group the Factors: \(2^6 = (2^3) \times (2^3)\)
- Extract the Cube Root: \(2^3 = 2\), so \(\sqrt[3]{2^6} = 2 \times 2 = 4\)
- Write the Simplified Form: \(\sqrt[3]{64} = 4\)
Let's try simplifying a cube root that includes a variable:
Example: Simplify \(\sqrt[3]{8x^9}\)
- Identify the Cube Root: \(\sqrt[3]{8x^9}\)
- Prime Factorization: \(8 = 2 \times 2 \times 2 = 2^3\), so \(8x^9 = 2^3 \times (x^3)^3\)
- Group the Factors: \((2^3) \times ((x^3)^3)\)
- Extract the Cube Root: \(2 \times x^3\)
- Write the Simplified Form: \(\sqrt[3]{8x^9} = 2x^3\)
By following these steps, you can simplify cube roots efficiently. Practice with different numbers and variables to master this technique.

Simplifying Radicals with Variables
Simplifying radicals that include variables involves several key steps. Here is a detailed, step-by-step process to help you simplify such expressions:
- Identify the Radical Expression:
For example, consider the expression \(\sqrt{50x^4}\).
- Prime Factorization:
Break down the number and the variable parts into their prime factors. For instance, \(50 = 2 \times 5^2\) and \(x^4 = (x^2)^2\).
- Separate the Radicals:
Write the expression as the product of square roots. For our example, \(\sqrt{50x^4} = \sqrt{2 \times 5^2 \times (x^2)^2}\).
- Simplify Each Part:
Take the square root of each part. For instance, \(\sqrt{2 \times 5^2 \times (x^2)^2} = \sqrt{2} \times \sqrt{5^2} \times \sqrt{(x^2)^2} = \sqrt{2} \times 5 \times x^2\).
- Combine the Results:
Combine the simplified parts outside the radical. Thus, \(\sqrt{50x^4} = 5x^2\sqrt{2}\).
Here are additional examples to illustrate the process:
Example 1: Simplify \(\sqrt{72y^3}\)
- Identify the Radical Expression: \(\sqrt{72y^3}\)
- Prime Factorization: \(72 = 2^3 \times 3^2\), so \(\sqrt{72y^3} = \sqrt{2^3 \times 3^2 \times y^3}\)
- Separate the Radicals: \(\sqrt{2^3 \times 3^2 \times y^3} = \sqrt{2^3} \times \sqrt{3^2} \times \sqrt{y^3}\)
- Simplify Each Part: \(\sqrt{2^3} = 2\sqrt{2}\), \(\sqrt{3^2} = 3\), \(\sqrt{y^3} = y\sqrt{y}\)
- Combine the Results: \(2 \times 3 \times y \sqrt{2y} = 6y\sqrt{2y}\)
Example 2: Simplify \(\sqrt{45a^6b^2}\)
- Identify the Radical Expression: \(\sqrt{45a^6b^2}\)
- Prime Factorization: \(45 = 3^2 \times 5\), so \(\sqrt{45a^6b^2} = \sqrt{3^2 \times 5 \times (a^3)^2 \times b^2}\)
- Separate the Radicals: \(\sqrt{3^2 \times 5 \times (a^3)^2 \times b^2} = \sqrt{3^2} \times \sqrt{5} \times \sqrt{(a^3)^2} \times \sqrt{b^2}\)
- Simplify Each Part: \(\sqrt{3^2} = 3\), \(\sqrt{5} = \sqrt{5}\), \(\sqrt{(a^3)^2} = a^3\), \(\sqrt{b^2} = b\)
- Combine the Results: \(3a^3b\sqrt{5}\)
By practicing these steps, you can become proficient at simplifying radicals with variables. Remember to factor completely and combine like terms where possible.
Special Considerations in Simplifying Radicals
When simplifying radical expressions, there are some special considerations to keep in mind to ensure accuracy and efficiency. Here are a few key points:
- Identifying Perfect Squares: Always look for perfect square factors within the radicand. For example, in \( \sqrt{50} \), the number 50 can be broken down into \( 25 \times 2 \), so \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \).
- Combining Like Radicals: Similar to combining like terms in algebra, only like radicals can be combined. For instance, \( 2\sqrt{3} + 5\sqrt{3} = 7\sqrt{3} \), but \( 2\sqrt{3} + 5\sqrt{2} \) cannot be combined.
- Rationalizing the Denominator: If a radical appears in the denominator, rationalize it by multiplying the numerator and denominator by a suitable radical. For example, \( \frac{1}{\sqrt{2}} \) can be rationalized by multiplying by \( \frac{\sqrt{2}}{\sqrt{2}} \), resulting in \( \frac{\sqrt{2}}{2} \).
- Handling Higher-Order Roots: When dealing with cube roots or higher-order roots, apply similar principles. For example, \( \sqrt[3]{8x^3} \) simplifies to \( 2x \) since 8 is a perfect cube and \( x^3 \) under the cube root simplifies to \( x \).
- Radicals with Variables: Apply the same rules to variables under the radical sign. For instance, \( \sqrt{x^4} = x^2 \) because \( x^4 \) is a perfect square.
By keeping these considerations in mind, you can simplify radical expressions more effectively and avoid common pitfalls.
Rationalizing the Denominator
Rationalizing the denominator involves converting a fraction with an irrational denominator into an equivalent fraction with a rational denominator. This process helps simplify the expression and can make further calculations easier. Here are the steps to rationalize the denominator:
-
Identify the irrational denominator:
Suppose you have a fraction with an irrational denominator, such as \( \frac{1}{\sqrt{2}} \).
-
Multiply numerator and denominator by the conjugate:
For simple square roots, multiply both the numerator and the denominator by the same irrational denominator:
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\] -
Rationalize more complex denominators:
If the denominator is a binomial involving a square root, multiply by its conjugate. For example, for \( \frac{1}{\sqrt{3} + 1} \), multiply by \( \sqrt{3} - 1 \):
\[
\frac{1}{\sqrt{3} + 1} \times \frac{\sqrt{3} - 1}{\sqrt{3} - 1} = \frac{\sqrt{3} - 1}{(\sqrt{3})^2 - 1^2} = \frac{\sqrt{3} - 1}{3 - 1} = \frac{\sqrt{3} - 1}{2}
\] -
Resulting simplified fraction:
After rationalizing, the denominator is now a rational number, and the expression is simplified.
Let’s practice rationalizing the denominator with a few examples:
-
Example 1: \( \frac{5}{\sqrt{7}} \)
\[
\frac{5}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}} = \frac{5\sqrt{7}}{7}
\] -
Example 2: \( \frac{3}{2 + \sqrt{5}} \)
\[
\frac{3}{2 + \sqrt{5}} \times \frac{2 - \sqrt{5}}{2 - \sqrt{5}} = \frac{3(2 - \sqrt{5})}{(2 + \sqrt{5})(2 - \sqrt{5})} = \frac{3(2 - \sqrt{5})}{4 - 5} = \frac{3(2 - \sqrt{5})}{-1} = -3(2 - \sqrt{5}) = -6 + 3\sqrt{5}
\]
These steps and examples show how to rationalize the denominator to simplify expressions and make them easier to work with in further calculations.
Combining Radical Expressions
Combining radical expressions involves simplifying expressions that contain radicals by combining like terms. Here's how you can do it:
- Identify like radicals: Ensure that the radicals have the same index and radicand.
- Combine coefficients: If the radicals are like, combine their coefficients.
- Simplify the expression: Perform any necessary arithmetic operations and simplify the final expression.
Let's look at some examples to illustrate these steps:
| Expression | Simplified Form |
|---|---|
| \(\sqrt{2} + 3\sqrt{2}\) | \((1 + 3)\sqrt{2} = 4\sqrt{2}\) |
| \(2\sqrt{3} - \sqrt{3}\) | \((2 - 1)\sqrt{3} = \sqrt{3}\) |
| \(5\sqrt{7} + 2\sqrt{7}\) | \((5 + 2)\sqrt{7} = 7\sqrt{7}\) |
When combining radicals with different indices or radicands, you cannot directly combine them. Instead, you should first try to simplify each radical expression individually and then see if they can be combined.
For example:
\(\sqrt{12} + 2\sqrt{3}\)
First, simplify \(\sqrt{12}\):
\(\sqrt{12} = \sqrt{4 \cdot 3} = 2\sqrt{3}\)
Now, the expression becomes:
\(2\sqrt{3} + 2\sqrt{3} = (2 + 2)\sqrt{3} = 4\sqrt{3}\)
Examples and Practice Problems
To master simplifying radical expressions, it is essential to practice with a variety of examples. Below are detailed examples and practice problems that will help reinforce your understanding.
Example 1: Simplifying the Square Root of 50
- Find the prime factorization of 50:
- \(50 = 2 \times 5^2\)
- Apply the property of square roots to simplify:
- \(\sqrt{50} = \sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2} = \sqrt{2} \times 5 = 5\sqrt{2}\)
Example 2: Simplifying the Cube Root of 54
- Find the prime factorization of 54:
- \(54 = 2 \times 3^3\)
- Apply the property of cube roots to simplify:
- \(\sqrt[3]{54} = \sqrt[3]{2 \times 3^3} = \sqrt[3]{2} \times \sqrt[3]{3^3} = \sqrt[3]{2} \times 3 = 3\sqrt[3]{2}\)
Example 3: Simplifying \(\sqrt{72a^3b^2}\)
- Find the prime factorization and separate variables:
- \(72 = 2^3 \times 3^2\)
- \(\sqrt{72a^3b^2} = \sqrt{2^3 \times 3^2 \times a^3 \times b^2}\)
- Apply the property of square roots to each part:
- \(\sqrt{72a^3b^2} = \sqrt{2^3} \times \sqrt{3^2} \times \sqrt{a^3} \times \sqrt{b^2}\)
- \(\sqrt{72a^3b^2} = \sqrt{2^2 \times 2} \times 3 \times a^{1.5} \times b = 6a^{1.5}b\)
Practice Problems
Try solving the following problems on your own:
- Simplify \(\sqrt{32}\).
- Simplify \(\sqrt[3]{125}\).
- Simplify \(\sqrt{50a^4b}\).
- Simplify \(\sqrt[3]{54x^3y^2}\).
Check your answers:
- \(\sqrt{32} = 4\sqrt{2}\)
- \(\sqrt[3]{125} = 5\)
- \(\sqrt{50a^4b} = 5a^2\sqrt{2b}\)
- \(\sqrt[3]{54x^3y^2} = 3x\sqrt[3]{2y^2}\)
Common Mistakes to Avoid
Simplifying radical expressions can be tricky, and there are several common mistakes students often make. Being aware of these can help you avoid them and simplify radicals correctly.
-
Incorrectly Simplifying Radicals:
Make sure to only combine like terms when simplifying radicals. For example, \(\sqrt{2}\) and \(\sqrt{3}\) cannot be combined because they are not like terms.
-
Forgetting to Simplify Completely:
Always check if the radical can be simplified further. For example, \(\sqrt{50}\) should be simplified to \(5\sqrt{2}\).
-
Not Rationalizing the Denominator:
It is important to rationalize the denominator to ensure the expression is in its simplest form. For example, \(\frac{1}{\sqrt{2}}\) should be rewritten as \(\frac{\sqrt{2}}{2}\).
-
Mistaking the Product Rule:
The product rule for radicals states that \(\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}\). However, this rule only applies to multiplication and not to addition or subtraction.
-
Incorrect Use of Exponents:
Remember that \(\sqrt{x} = x^{1/2}\) and \(\sqrt[3]{x} = x^{1/3}\). Misapplying these rules can lead to incorrect simplification.
-
Combining Radicals Incorrectly:
Ensure you only combine radicals with the same index and radicand. For example, \(\sqrt{2} + \sqrt{8}\) can be simplified to \(3\sqrt{2}\) because \(\sqrt{8} = 2\sqrt{2}\).
Advanced Techniques in Simplifying Radicals
When simplifying radicals, there are advanced techniques that can make the process more efficient and accurate. These techniques often involve higher-level algebraic manipulations and a deep understanding of the properties of radicals. Below, we outline some of these advanced methods.
Using Conjugates
One powerful technique is to use conjugates to simplify expressions involving radicals. The conjugate of an expression is formed by changing the sign between two terms. For example, the conjugate of \(a + b\) is \(a - b\).
Consider the expression \(\frac{1}{\sqrt{5} + 2}\). To rationalize the denominator, multiply by the conjugate:
- Identify the conjugate: \(\sqrt{5} - 2\).
- Multiply the numerator and the denominator by the conjugate: \[ \frac{1}{\sqrt{5} + 2} \cdot \frac{\sqrt{5} - 2}{\sqrt{5} - 2} = \frac{\sqrt{5} - 2}{(\sqrt{5})^2 - 2^2} = \frac{\sqrt{5} - 2}{5 - 4} = \sqrt{5} - 2. \]
Combining Like Radicals
Combining like radicals involves treating radicals similar to like terms in algebra. Only radicals with the same index and radicand can be combined.
For example, to simplify \(3\sqrt{2} + 5\sqrt{2}\), combine the coefficients:
\[
3\sqrt{2} + 5\sqrt{2} = (3 + 5)\sqrt{2} = 8\sqrt{2}.
\]
Advanced Factoring Techniques
In some cases, factoring can simplify complex radical expressions. Look for opportunities to factor out common terms or use special factoring formulas.
For example, consider \(\sqrt{12x^2}\):
\[
\sqrt{12x^2} = \sqrt{4 \cdot 3x^2} = \sqrt{4} \cdot \sqrt{3x^2} = 2x\sqrt{3}.
\]
Radicals in Higher Dimensions
For higher-dimensional problems, such as those involving multiple variables or complex numbers, understanding the properties of radicals in these contexts is crucial. Techniques like polar form conversion and Euler's formula may be useful.
Example Problem
Simplify the expression \(\frac{3 + \sqrt{5}}{2 - \sqrt{3}}\):
- Multiply by the conjugate of the denominator: \[ \frac{3 + \sqrt{5}}{2 - \sqrt{3}} \cdot \frac{2 + \sqrt{3}}{2 + \sqrt{3}} = \frac{(3 + \sqrt{5})(2 + \sqrt{3})}{(2 - \sqrt{3})(2 + \sqrt{3})}. \]
- Expand and simplify: \[ = \frac{6 + 3\sqrt{3} + 2\sqrt{5} + \sqrt{15}}{4 - 3} = 6 + 3\sqrt{3} + 2\sqrt{5} + \sqrt{15}. \]
By mastering these advanced techniques, you can handle more complex radical expressions with confidence and precision.
Applications of Simplifying Radical Expressions
Understanding how to simplify radical expressions is crucial not only for solving mathematical problems but also for applying these concepts in various real-world scenarios. Here are some applications of simplifying radical expressions:
- Geometry:
In geometry, simplified radicals are often used to express the lengths of sides of right triangles and other geometric shapes. For example, the Pythagorean theorem frequently results in expressions that require simplification of square roots.
Example: In a right triangle with legs of lengths 3 and 4, the hypotenuse is \( \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \).
- Physics:
Physics problems often involve calculations with radicals, especially when dealing with formulas for motion, energy, and waves. Simplifying these expressions can make calculations more manageable.
Example: The formula for the period of a pendulum is \( T = 2\pi \sqrt{\frac{L}{g}} \), where \( L \) is the length of the pendulum and \( g \) is the acceleration due to gravity. Simplifying the expression under the square root can help in understanding and solving the problem.
- Engineering:
Engineering disciplines use radical expressions in design and analysis. For example, electrical engineering often requires simplification of expressions involving impedance and resonance frequencies.
Example: The resonant frequency of an RLC circuit is given by \( f = \frac{1}{2\pi\sqrt{LC}} \), where \( L \) is inductance and \( C \) is capacitance.
- Computer Science:
In computer algorithms, particularly those involving computational geometry and graphics, simplifying radical expressions can optimize performance and accuracy.
Example: Calculating distances in coordinate systems often involves square roots, such as the Euclidean distance formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
By mastering the simplification of radical expressions, students and professionals can enhance their problem-solving skills and apply these techniques effectively in various fields.
Additional Resources and References
For those looking to deepen their understanding of simplifying radical expressions, the following resources offer comprehensive lessons and practice opportunities:
-
This unit covers the basics of exponents and radicals, including simplifying square roots and higher-index roots. It provides video lessons and practice exercises to reinforce the concepts.
-
Here, you will find in-depth explanations of rational exponents and how they relate to radicals, along with practice problems to test your skills.
-
This section focuses on solving and graphing radical equations, helping students apply their knowledge of radicals in different contexts.
Recommended Reading
-
Detailed tutorials on simplifying radical expressions, including step-by-step instructions and examples.
-
A thorough mathematical reference that covers the theory and properties of radicals.
Practice Problems
| Resource | Description | Link |
|---|---|---|
| Khan Academy Practice | Interactive problems and quizzes on simplifying radicals. | |
| Math is Fun Worksheets | Printable worksheets to practice simplifying radical expressions. |
These resources should provide a solid foundation and ample practice opportunities to master simplifying radical expressions.
Hướng dẫn đơn giản hóa biểu thức căn bậc 2 với Khan Academy. Học cách làm chủ các biểu thức căn bậc 2 một cách dễ dàng và hiệu quả.
Đơn Giản Hóa Biểu Thức Căn Bậc 2 1
READ MORE:
Học cách thêm và đơn giản hóa căn thức trong toán sơ cấp với Khan Academy. Nâng cao kỹ năng giải toán của bạn với các bài học và ví dụ thực tế.
Thêm và Đơn Giản Hóa Căn Thức | Toán Sơ Cấp | Khan Academy