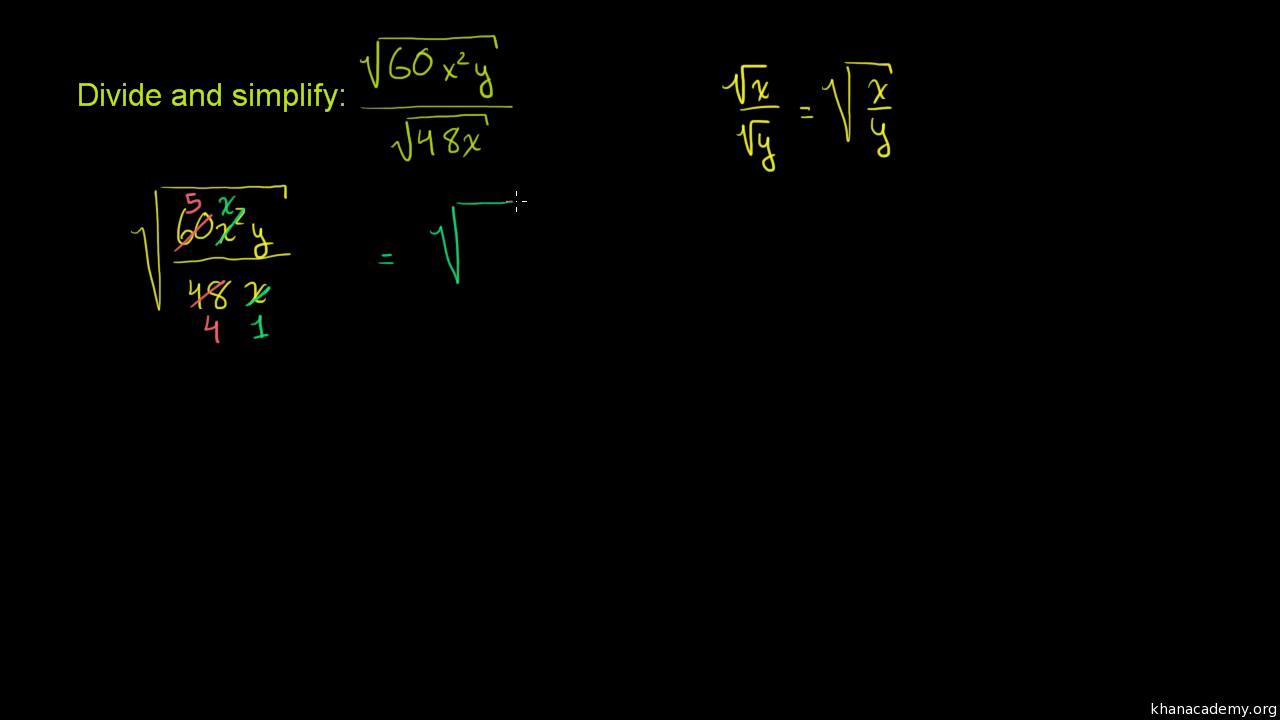Topic simplifying radical expressions answer key: Unlock the secrets to mastering radical expressions with our comprehensive answer key. Dive into clear explanations and step-by-step solutions that simplify even the most complex radicals. Perfect for students and educators alike, this guide ensures you gain a solid understanding of the fundamental principles and advanced techniques required to simplify radical expressions effectively.
Table of Content
- Simplifying Radical Expressions Answer Key
- Introduction to Simplifying Radical Expressions
- Properties of Radicals
- Simplifying Square Roots Using the Product Property
- Examples of Simplifying Square Roots
- Simplifying Radical Expressions with Variables
- Simplifying Higher-Order Radicals
- Multiplying and Dividing Radical Expressions
- Rationalizing the Denominator
- Common Mistakes to Avoid
- Practice Problems and Answer Key
- YOUTUBE:
Simplifying Radical Expressions Answer Key
Below are some common examples and methods for simplifying radical expressions.
Example 1: Simplify \( \sqrt[3]{27x^3} \)
Solution: Use the fact that \( \sqrt[n]{a^n} = a \) when \( n \) is odd.
\[
\sqrt[3]{27x^3} = \sqrt[3]{3^3 \cdot x^3} = \sqrt[3]{3^3} \cdot \sqrt[3]{x^3} = 3x
\]
Example 2: Simplify \( \sqrt[4]{16y^4} \)
Solution: Use the fact that \( \sqrt[n]{a^n} = |a| \) when \( n \) is even.
\[
\sqrt[4]{16y^4} = \sqrt[4]{2^4 y^4} = \sqrt[4]{2^4} \cdot \sqrt[4]{y^4} = 2|y|
\]
Example 3: Simplify \( \sqrt{98} \)
Solution: Find the largest factor in the radicand that is a perfect power of the index.
\[
\sqrt{98} = \sqrt{49 \cdot 2} = \sqrt{49} \cdot \sqrt{2} = 7\sqrt{2}
\]
Example 4: Simplify \( \sqrt{48} \)
Solution: Find the largest perfect square factor.
\[
\sqrt{48} = \sqrt{16 \cdot 3} = \sqrt{16} \cdot \sqrt{3} = 4\sqrt{3}
\]
Example 5: Simplify \( \sqrt{72} \)
Solution: Use the product rule for square roots.
\[
\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}
\]
Example 6: Simplify \( \sqrt{200} \)
Solution: Use the product rule for square roots.
\[
\sqrt{200} = \sqrt{100 \cdot 2} = \sqrt{100} \cdot \sqrt{2} = 10\sqrt{2}
\]
Example 7: Simplify \( \sqrt{54a^{10}b^{16}c^7} \)
Solution: Use the product rule and simplify each part separately.
\[
\sqrt{54a^{10}b^{16}c^7} = \sqrt{54} \cdot \sqrt{a^{10}} \cdot \sqrt{b^{16}} \cdot \sqrt{c^7} = 3a^5b^8c^3\sqrt{6c}
\]
Example 8: Simplify \( \sqrt{12x^2y^4} \)
Solution: Simplify the numerical and variable parts separately.
\[
\sqrt{12x^2y^4} = \sqrt{4 \cdot 3x^2y^4} = \sqrt{4} \cdot \sqrt{3} \cdot \sqrt{x^2} \cdot \sqrt{y^4} = 2xy^2\sqrt{3}
\]
Tips for Simplifying Radical Expressions
- Look for the largest perfect square factor of the radicand.
- Use the product rule: \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Simplify the variables by breaking them into pairs.
- Always check your final answer by simplifying further if possible.

READ MORE:
Introduction to Simplifying Radical Expressions
Simplifying radical expressions involves expressing them in their simplest form. A radical expression includes a root symbol, and our goal is to make these expressions as straightforward as possible using various mathematical properties and rules.
Radical expressions can be simplified by using the product and quotient rules for radicals:
- Product Rule: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Rule: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \(b \neq 0\)
When simplifying radical expressions, we typically follow these steps:
- Factor the radicand: Write the number under the radical as a product of its prime factors.
- Apply the product rule: Use the product rule to separate the radical into simpler parts.
- Simplify each radical: Simplify the radicals by bringing out any perfect squares (or higher powers for higher-order roots).
- Combine the simplified radicals: Multiply the simplified parts back together.
Here are some examples to illustrate the process:
Example 1: Simplify \(\sqrt{72}\)
We start by factoring 72 into prime factors:
\(\sqrt{72} = \sqrt{2^3 \cdot 3^2} = \sqrt{(2^2 \cdot 3^2) \cdot 2} = \sqrt{4 \cdot 9 \cdot 2} = \sqrt{36 \cdot 2}\)
Applying the product rule and simplifying:
\(\sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}\)
Example 2: Simplify \(\sqrt{50x^4y^6}\)
We start by factoring the radicand:
\(\sqrt{50x^4y^6} = \sqrt{2 \cdot 5^2 \cdot x^4 \cdot y^6} = \sqrt{2 \cdot (5^2) \cdot (x^2)^2 \cdot (y^3)^2}\)
Applying the product rule and simplifying:
\(\sqrt{2 \cdot (5^2) \cdot (x^2)^2 \cdot (y^3)^2} = 5x^2y^3\sqrt{2}\)
By understanding and applying these basic rules, you can simplify most radical expressions, making complex algebraic expressions more manageable and easier to work with.
Properties of Radicals
Radicals, also known as roots, have specific properties that are essential for simplifying radical expressions. Understanding these properties helps in performing operations involving radicals efficiently. Below are the key properties of radicals:
- Product Property: The product of two radicals is equal to the radical of the product. This property can be expressed as:
- Quotient Property: The quotient of two radicals is equal to the radical of the quotient. This property can be expressed as:
- Power Property: The radical of a number raised to a power can be simplified by dividing the exponent by the index of the radical. This property is expressed as:
- Combining Like Radicals: Similar to combining like terms, radicals with the same radicand and index can be combined by adding or subtracting their coefficients.
These properties are fundamental in simplifying radical expressions and performing various operations with radicals. Mastery of these properties enables solving more complex algebraic problems involving radicals.
Simplifying Square Roots Using the Product Property
The Product Property of Square Roots allows us to simplify square roots by breaking down the radicand into smaller, manageable parts. This property states that the square root of a product is equal to the product of the square roots of each factor. In mathematical terms, if a and b are nonnegative numbers, then:
\[ \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \]
Here's a step-by-step guide to simplifying square roots using the Product Property:
- Factor any perfect squares out of the radicand.
- Rewrite the square root as a product of the square roots of each factor.
- Simplify each square root individually.
Let's look at a few examples to understand this better:
Example 1
Simplify \( \sqrt{72} \).
- Factor the radicand: \( 72 = 36 \times 2 \).
- Apply the Product Property: \( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \cdot \sqrt{2} \).
- Simplify each square root: \( \sqrt{36} = 6 \), so \( \sqrt{72} = 6 \cdot \sqrt{2} = 6\sqrt{2} \).
Example 2
Simplify \( \sqrt{50x^2y^3z} \).
- Factor the radicand: \( 50x^2y^3z = 25 \times 2 \times x^2 \times y^2 \times y \times z \).
- Apply the Product Property: \( \sqrt{50x^2y^3z} = \sqrt{25} \cdot \sqrt{2} \cdot \sqrt{x^2} \cdot \sqrt{y^2} \cdot \sqrt{y} \cdot \sqrt{z} \).
- Simplify each square root: \( \sqrt{25} = 5 \), \( \sqrt{x^2} = x \), \( \sqrt{y^2} = y \), so \( \sqrt{50x^2y^3z} = 5xy \sqrt{2yz} \).
Using the Product Property, you can break down complex square roots into simpler components, making them easier to work with and understand.
Examples of Simplifying Square Roots
Simplifying square roots involves finding the largest perfect square factor of the radicand (the number inside the square root symbol) and then using the product property of square roots. Here are some detailed examples:
-
Example 1: Simplify \(\sqrt{72}\)
- Identify the largest perfect square factor of 72. The perfect square factors of 72 are 4, 9, and 36. The largest perfect square factor is 36.
- Rewrite 72 as a product of 36 and 2: \(\sqrt{72} = \sqrt{36 \cdot 2}\).
- Apply the product property of square roots: \(\sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2}\).
- Simplify: \(\sqrt{36} = 6\), so \(\sqrt{72} = 6\sqrt{2}\).
-
Example 2: Simplify \(\sqrt{48}\)
- Identify the largest perfect square factor of 48. The perfect square factors of 48 are 4 and 16. The largest perfect square factor is 16.
- Rewrite 48 as a product of 16 and 3: \(\sqrt{48} = \sqrt{16 \cdot 3}\).
- Apply the product property of square roots: \(\sqrt{16 \cdot 3} = \sqrt{16} \cdot \sqrt{3}\).
- Simplify: \(\sqrt{16} = 4\), so \(\sqrt{48} = 4\sqrt{3}\).
-
Example 3: Simplify \(\sqrt{200}\)
- Identify the largest perfect square factor of 200. The perfect square factors of 200 are 4, 25, and 100. The largest perfect square factor is 100.
- Rewrite 200 as a product of 100 and 2: \(\sqrt{200} = \sqrt{100 \cdot 2}\).
- Apply the product property of square roots: \(\sqrt{100 \cdot 2} = \sqrt{100} \cdot \sqrt{2}\).
- Simplify: \(\sqrt{100} = 10\), so \(\sqrt{200} = 10\sqrt{2}\).
-
Example 4: Simplify \(\sqrt{180}\)
- Identify the largest perfect square factor of 180. The perfect square factors of 180 are 4, 9, and 36. The largest perfect square factor is 36.
- Rewrite 180 as a product of 36 and 5: \(\sqrt{180} = \sqrt{36 \cdot 5}\).
- Apply the product property of square roots: \(\sqrt{36 \cdot 5} = \sqrt{36} \cdot \sqrt{5}\).
- Simplify: \(\sqrt{36} = 6\), so \(\sqrt{180} = 6\sqrt{5}\).
By practicing these examples, you will get better at recognizing perfect square factors and applying the product property to simplify square roots efficiently.
Simplifying Radical Expressions with Variables
When simplifying radical expressions that include variables, it's important to follow a systematic approach. Here's a detailed step-by-step guide:
-
Identify and Separate Factors:
Start by expressing the number and variables under the radical sign as a product of their prime factors.
Example: \(\sqrt{100x^4y^6z^3}\)
Write it as a product of prime factors and variables:
\(\sqrt{2 \times 2 \times 5 \times 5 \times x \times x \times x \times x \times y \times y \times y \times y \times y \times y \times z \times z \times z}\)
-
Pair Identical Factors:
Group the factors in pairs of identical factors:
\(\sqrt{(2^2 \times 5^2 \times (x^2)^2 \times (y^3)^2 \times z^2 \times z)}\)
-
Simplify the Radical:
Extract the pairs from under the radical:
\(\sqrt{2^2 \times 5^2 \times (x^2)^2 \times (y^3)^2 \times z^2 \times z} = 2 \times 5 \times x^2 \times |y^3| \times |z| \times \sqrt{z}\)
-
Combine and Simplify Further:
Multiply the extracted factors:
\(2 \times 5 \times x^2 \times |y^3| \times |z| \times \sqrt{z} = 10x^2|y^3||z|\sqrt{z}\)
Here are additional tips and rules for simplifying radical expressions with variables:
- Product and Quotient Rules:
- \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}, \, b \neq 0\)
- Non-negative Results: Always use the absolute value symbol to ensure non-negative results, as the square root of a number is always non-negative.
- Assumption of Positivity: Typically, variables are assumed to be positive to simplify the calculation without the need for absolute values.
By following these steps and rules, you can simplify complex radical expressions involving variables efficiently.
Simplifying Higher-Order Radicals
Simplifying higher-order radicals involves breaking down the expression inside the radical into its prime factors and then simplifying. Here are the steps to simplify higher-order radicals:
- Identify the index of the radical. The index is the small number outside and to the left of the radical symbol. For example, in (the fifth root), the index is 5.
- Factor the radicand (the number inside the radical) into its prime factors. For example, for the fifth root of 32, factor 32 into its prime factors: .
- Rewrite the radicand as a product of powers that match the index of the radical. For instance, can be written as .
- Simplify by taking out the factors that match the index. In this case,
Here are some examples to illustrate the process:
- Example 1: Simplify
- Factor the radicand:
- Rewrite using the index:
- Simplify:
- Example 2: Simplify
- Factor the radicand:
- Rewrite using the index:
- Simplify:
- Example 3: Simplify
- Factor the radicand:
- Rewrite using the index:
- Simplify:
In addition to numerical examples, let's consider an example involving variables:
- Example 4: Simplify
- Factor the radicand:
- Rewrite using the index:
- Simplify:
Multiplying and Dividing Radical Expressions
When working with radical expressions, it is essential to understand how to multiply and divide them effectively. Here are the steps and rules to follow:
Multiplying Radical Expressions
To multiply radical expressions, use the product rule for radicals, which states that \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\), provided that a and b are non-negative.
- Multiply the coefficients (numbers outside the radicals).
- Multiply the radicands (numbers inside the radicals).
- Simplify the resulting radical if possible.
For example:
\[
\sqrt{2} \cdot \sqrt{3} = \sqrt{2 \cdot 3} = \sqrt{6}
\]
Another example with variables:
\[
2\sqrt{5x} \cdot 3\sqrt{2x^2} = (2 \cdot 3)\sqrt{5x \cdot 2x^2} = 6\sqrt{10x^3}
\]
Simplify the radical:
\[
6\sqrt{10x^3} = 6\sqrt{10x^2 \cdot x} = 6x\sqrt{10x}
\]
Dividing Radical Expressions
To divide radical expressions, use the quotient rule for radicals, which states that \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), provided that b ≠ 0.
- Divide the coefficients.
- Divide the radicands.
- Simplify the resulting radical if possible.
For example:
\[
\frac{\sqrt{18}}{\sqrt{2}} = \sqrt{\frac{18}{2}} = \sqrt{9} = 3
\]
Another example with variables:
\[
\frac{6\sqrt{24x^3}}{3\sqrt{2x}} = \frac{6}{3} \cdot \frac{\sqrt{24x^3}}{\sqrt{2x}} = 2 \cdot \sqrt{\frac{24x^3}{2x}} = 2 \cdot \sqrt{12x^2} = 2 \cdot \sqrt{4 \cdot 3x^2} = 2 \cdot 2x\sqrt{3} = 4x\sqrt{3}
\]
Rationalizing the Denominator
When you have a radical expression in the denominator, you should rationalize it by eliminating the radical. Multiply the numerator and denominator by the conjugate of the denominator or an appropriate radical to achieve this.
For example:
\[
\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Another example:
\[
\frac{3}{2 + \sqrt{5}} = \frac{3(2 - \sqrt{5})}{(2 + \sqrt{5})(2 - \sqrt{5})} = \frac{3(2 - \sqrt{5})}{4 - 5} = \frac{3(2 - \sqrt{5})}{-1} = -3(2 - \sqrt{5}) = -6 + 3\sqrt{5}
\]
These rules and examples should help in simplifying, multiplying, and dividing radical expressions effectively. Practice with various problems to become proficient in these techniques.
Rationalizing the Denominator
Rationalizing the denominator is a method used to eliminate radicals from the denominator of a fraction. This process involves multiplying both the numerator and the denominator by a suitable radical that will make the denominator a rational number.
Step-by-Step Process
Let's explore how to rationalize the denominator with a few examples:
Example 1: Rationalizing a Single Term in the Denominator
Simplify the expression \(\frac{1}{\sqrt{2}}\).
- Identify the radical in the denominator: \(\sqrt{2}\).
- Multiply both the numerator and the denominator by \(\sqrt{2}\) to eliminate the radical:
- The simplified expression is \(\frac{\sqrt{2}}{2}\).
\[
\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}.
\]
Example 2: Rationalizing with a Binomial Denominator
Simplify the expression \(\frac{1}{1+\sqrt{3}}\).
- Identify the binomial in the denominator: \(1+\sqrt{3}\).
- Multiply both the numerator and the denominator by the conjugate of the denominator, \(1-\sqrt{3}\):
- Apply the difference of squares formula to the denominator: \((1+\sqrt{3})(1-\sqrt{3}) = 1 - 3 = -2\).
- The simplified expression is \(\frac{1-\sqrt{3}}{-2}\), or \(-\frac{1-\sqrt{3}}{2}\).
\[
\frac{1}{1+\sqrt{3}} \times \frac{1-\sqrt{3}}{1-\sqrt{3}} = \frac{1-\sqrt{3}}{(1+\sqrt{3})(1-\sqrt{3})}.
\]
Example 3: Rationalizing with Variables
Simplify the expression \(\frac{5}{\sqrt{a} + \sqrt{b}}\).
- Identify the binomial in the denominator: \(\sqrt{a} + \sqrt{b}\).
- Multiply both the numerator and the denominator by the conjugate of the denominator, \(\sqrt{a} - \sqrt{b}\):
- Apply the difference of squares formula to the denominator: \((\sqrt{a} + \sqrt{b})(\sqrt{a} - \sqrt{b}) = a - b\).
- The simplified expression is \(\frac{5(\sqrt{a} - \sqrt{b})}{a - b}\).
\[
\frac{5}{\sqrt{a} + \sqrt{b}} \times \frac{\sqrt{a} - \sqrt{b}}{\sqrt{a} - \sqrt{b}} = \frac{5(\sqrt{a} - \sqrt{b})}{(\sqrt{a} + \sqrt{b})(\sqrt{a} - \sqrt{b})}.
\]
Practice Problems
- Simplify \(\frac{3}{\sqrt{5}}\).
- Simplify \(\frac{2}{1 + \sqrt{2}}\).
- Simplify \(\frac{4}{\sqrt{x} - \sqrt{y}}\).
By following these steps, you can rationalize the denominator in any radical expression, making it easier to work with and understand.
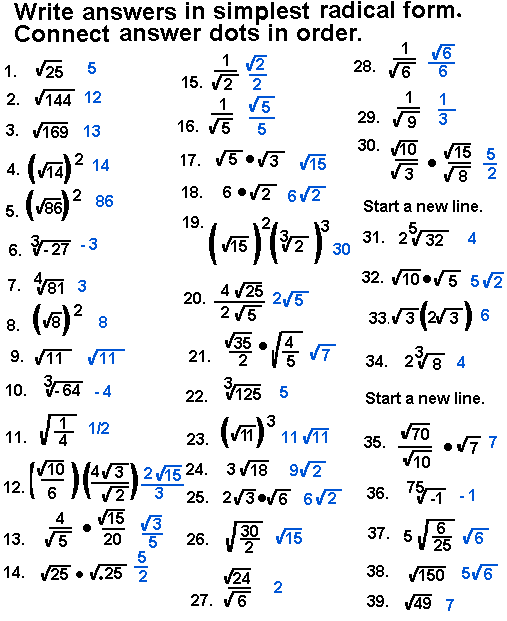
Common Mistakes to Avoid
When simplifying radical expressions, students often make several common mistakes. Understanding and avoiding these errors can help ensure accurate and simplified results.
- Incorrectly Applying the Product Property:
The product property of radicals states that \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\). A common mistake is to assume that this property can be applied to sums or differences, such as \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\), which is incorrect. For example, \(\sqrt{9 + 16} \neq \sqrt{9} + \sqrt{16}\), since \(\sqrt{25} \neq 3 + 4\).
- Forgetting to Simplify Completely:
Another frequent error is not simplifying the radical expression completely. Always factor the radicand (the number under the radical sign) into its prime factors and simplify. For example, \(\sqrt{72}\) should be simplified to \(6\sqrt{2}\), not just \(\sqrt{36 \cdot 2}\).
- Incorrectly Combining Radicals:
Only like radicals can be combined. A mistake occurs when trying to add or subtract radicals with different radicands. For instance, \(\sqrt{3} + \sqrt{5}\) cannot be simplified further because the radicands are different.
- Ignoring the Domain Restrictions:
Radical expressions, especially even-order roots, have restrictions on their domains. Ensure that the radicand is non-negative for square roots and even roots to avoid dealing with imaginary numbers in real number contexts.
- Rationalizing Incorrectly:
When rationalizing the denominator, ensure the process is done correctly by multiplying by the conjugate if necessary. For example, to rationalize \(\frac{1}{\sqrt{2} + 1}\), multiply by the conjugate \(\sqrt{2} - 1\) to get \(\frac{\sqrt{2} - 1}{1}\).
By being aware of these common mistakes and understanding the correct methods for simplifying radicals, you can avoid these pitfalls and accurately simplify radical expressions.
Practice Problems and Answer Key
Below are several practice problems to help you master simplifying radical expressions. Each problem is followed by its solution to allow for self-assessment and understanding.
-
Simplify the expression: \( \sqrt{50} \)
Solution:
\[
\begin{aligned}
\sqrt{50} &= \sqrt{25 \cdot 2} \\
&= \sqrt{25} \cdot \sqrt{2} \\
&= 5\sqrt{2}
\end{aligned}
\] -
Simplify the expression: \( \sqrt{18x^{3}} \)
Solution:
\[
\begin{aligned}
\sqrt{18x^{3}} &= \sqrt{9 \cdot 2 \cdot x^{2} \cdot x} \\
&= \sqrt{9} \cdot \sqrt{2} \cdot \sqrt{x^{2}} \cdot \sqrt{x} \\
&= 3x\sqrt{2x}
\end{aligned}
\] -
Simplify the expression: \( \frac{\sqrt{12}}{\sqrt{3}} \)
Solution:
\[
\begin{aligned}
\frac{\sqrt{12}}{\sqrt{3}} &= \frac{\sqrt{4 \cdot 3}}{\sqrt{3}} \\
&= \frac{\sqrt{4} \cdot \sqrt{3}}{\sqrt{3}} \\
&= \frac{2\sqrt{3}}{\sqrt{3}} \\
&= 2
\end{aligned}
\] -
Simplify the expression: \( \sqrt[3]{54a^{6}b^{3}} \)
Solution:
\[
\begin{aligned}
\sqrt[3]{54a^{6}b^{3}} &= \sqrt[3]{27 \cdot 2 \cdot a^{6} \cdot b^{3}} \\
&= \sqrt[3]{27} \cdot \sqrt[3]{2} \cdot \sqrt[3]{a^{6}} \cdot \sqrt[3]{b^{3}} \\
&= 3a^{2}b\sqrt[3]{2}
\end{aligned}
\] -
Simplify the expression: \( \sqrt{\frac{32x^{5}}{y^{2}}} \)
Solution:
\[
\begin{aligned}
\sqrt{\frac{32x^{5}}{y^{2}}} &= \frac{\sqrt{32x^{5}}}{\sqrt{y^{2}}} \\
&= \frac{\sqrt{16 \cdot 2 \cdot x^{4} \cdot x}}{y} \\
&= \frac{4x^{2}\sqrt{2x}}{y}
\end{aligned}
\]
These problems should provide a good range of practice for simplifying radical expressions, covering various types of expressions and techniques. Be sure to review each solution carefully and practice additional problems to reinforce your understanding.
Giải Pháp Bài Tập Rút Gọn Căn Thức
READ MORE:
Đáp Án Bài Tập Rút Gọn Căn Thức