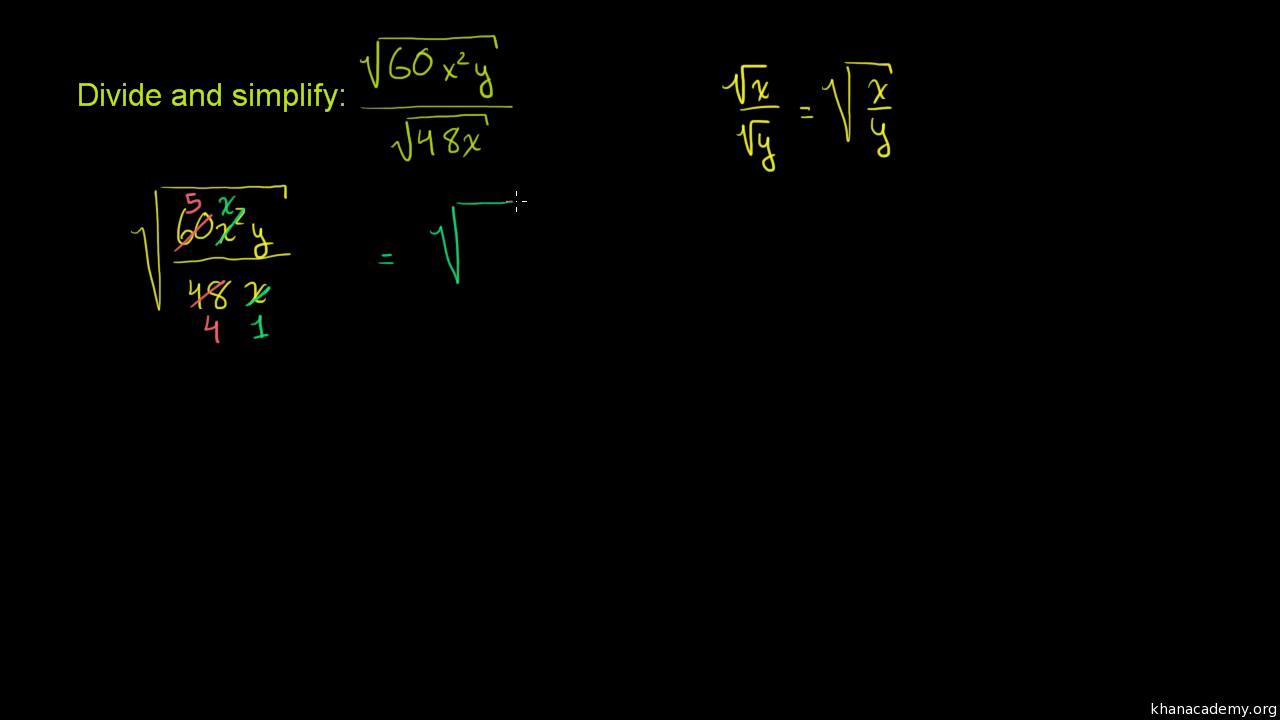10-2 Skills Practice: Simplifying Radical Expressions Made Easy

Radical expressions are expressions that contain a square root, cube root, or any higher-order root. Simplifying these expressions involves expressing them in their simplest form. Here are some common techniques and examples:

Product Property of Radicals

The product property states that the square root of a product is equal to the product of the square roots:

\(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)

Example:

\(\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\)

Quotient Property of Radicals

The quotient property states that the square root of a quotient is equal to the quotient of the square roots:

\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)

Example:

\(\sqrt{\frac{49}{4}} = \frac{\sqrt{49}}{\sqrt{4}} = \frac{7}{2}\)

Combining Like Radicals

Similar to combining like terms, like radicals can be added or subtracted:

Example:

\(2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}\)

Rationalizing the Denominator

To eliminate a radical from the denominator, multiply both the numerator and the denominator by a suitable radical:

Example:

\(\frac{5}{\sqrt{2}} = \frac{5 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{5\sqrt{2}}{2}\)

Practice Problems

1. \(\sqrt{72} = \sqrt{36 \cdot 2} = 6\sqrt{2}\)
2. \(\sqrt{99} = \sqrt{9 \cdot 11} = 3\sqrt{11}\)
3. \(\sqrt{128} = \sqrt{64 \cdot 2} = 8\sqrt{2}\)
4. \(\frac{\sqrt{50}}{\sqrt{2}} = \sqrt{\frac{50}{2}} = \sqrt{25} = 5\)

Additional Examples

• \(\sqrt{80} = \sqrt{16 \cdot 5} = 4\sqrt{5}\)
• \(3\sqrt{12} + 2\sqrt{27} = 3 \cdot 2\sqrt{3} + 2 \cdot 3\sqrt{3} = 6\sqrt{3} + 6\sqrt{3} = 12\sqrt{3}\)

By following these steps and practicing with various problems, you can become proficient at simplifying radical expressions.

Simplifying radical expressions involves rewriting expressions that contain roots in their simplest form. Here are some essential steps and properties used in the simplification process:

• Identify Perfect Powers: Determine if the radicand (the number under the radical sign) has any perfect power factors. For example, in \(\sqrt{50}\), the number 50 can be factored into \(25 \times 2\), where 25 is a perfect square.
• Use the Product Property: Apply the product property of roots, which states \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\). For instance, \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\).
• Combine Like Terms: If you have similar radical terms, combine them just like you would with regular algebraic terms. For example, \(3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}\).
• Rationalizing the Denominator: If a radical appears in the denominator, multiply the numerator and the denominator by a radical that will eliminate the radical in the denominator. For example, to rationalize \(\frac{1}{\sqrt{2}}\), multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\) to get \(\frac{\sqrt{2}}{2}\).

By following these steps, you can simplify any radical expression efficiently and correctly. Mastering these techniques is crucial for solving more complex algebraic problems involving radicals.

Understanding the properties of radicals is crucial for simplifying radical expressions effectively. Here are some key properties:

• Product Property: \(\sqrt[n]{ab} = \sqrt[n]{a} \cdot \sqrt[n]{b}\)
• Quotient Property: \(\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}\) (for \(b \ne 0\))
• Power of a Radical: \(\left(\sqrt[n]{a}\right)^m = a^{\frac{m}{n}}\)

Using these properties, you can simplify complex radical expressions by breaking them into simpler parts and recombining them. Let's look at an example:

Example: Simplify \(\sqrt[3]{54}\)

1. Factor the radicand: \(54 = 27 \cdot 2\)
2. Apply the product property: \(\sqrt[3]{54} = \sqrt[3]{27 \cdot 2} = \sqrt[3]{27} \cdot \sqrt[3]{2}\)
3. Simplify: \(\sqrt[3]{27} = 3\), so \(\sqrt[3]{54} = 3\sqrt[3]{2}\)

By understanding and applying these properties, you can simplify any radical expression systematically and accurately.

To simplify square roots, we use the property that the square root of a product is the product of the square roots. This is known as the Product Property of Square Roots:

\[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \]

Follow these steps to simplify a square root:

1. Identify perfect square factors: Look for the largest perfect square factor of the radicand (the number inside the square root).
2. Rewrite the radicand: Express the radicand as a product of the perfect square factor and another factor.
3. Apply the product property: Use the product property to separate the square root into the product of two square roots.
4. Simplify: Simplify the square root of the perfect square factor.

Here are some examples to illustrate the process:

• Example 1: Simplify \( \sqrt{72} \).
  • Identify perfect square factors: 36 is a perfect square factor of 72.
  • Rewrite the radicand: \( 72 = 36 \times 2 \).
  • Apply the product property: \( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \cdot \sqrt{2} \).
  • Simplify: \( \sqrt{36} = 6 \), so \( \sqrt{72} = 6\sqrt{2} \).
• Example 2: Simplify \( \sqrt{50} \).
  • Identify perfect square factors: 25 is a perfect square factor of 50.
  • Rewrite the radicand: \( 50 = 25 \times 2 \).
  • Apply the product property: \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \cdot \sqrt{2} \).
  • Simplify: \( \sqrt{25} = 5 \), so \( \sqrt{50} = 5\sqrt{2} \).
• Example 3: Simplify \( \sqrt{200} \).
  • Identify perfect square factors: 100 is a perfect square factor of 200.
  • Rewrite the radicand: \( 200 = 100 \times 2 \).
  • Apply the product property: \( \sqrt{200} = \sqrt{100 \times 2} = \sqrt{100} \cdot \sqrt{2} \).
  • Simplify: \( \sqrt{100} = 10 \), so \( \sqrt{200} = 10\sqrt{2} \).

By following these steps, you can simplify any square root expression.

Simplifying higher-order roots, such as cube roots or fourth roots, involves a process similar to simplifying square roots. We use the properties of radicals, specifically the product and quotient properties, to break down the radicand into simpler components. Here is a step-by-step guide:

Steps to Simplify Higher-Order Roots

1. Identify the Index: Determine the index of the radical (e.g., 3 for cube roots, 4 for fourth roots).
2. Find Perfect Powers: Find the largest factor in the radicand that is a perfect power of the index.
3. Rewrite the Radicand: Express the radicand as a product of two factors, with one being the perfect power identified.
4. Apply the Product Property: Use the product property of radicals to split the radical into two simpler radicals.
5. Simplify: Simplify the root of the perfect power.

Examples

Example 1: Simplifying a Cube Root

Simplify: \( \sqrt[3]{54} \)

1. Identify the index: 3.
2. Find the largest perfect cube factor of 54. Here, \( 27 \) is the largest perfect cube factor.
3. Rewrite the radicand: \( 54 = 27 \times 2 \).
4. Apply the product property: \( \sqrt[3]{54} = \sqrt[3]{27 \times 2} = \sqrt[3]{27} \times \sqrt[3]{2} \).
5. Simplify: \( \sqrt[3]{27} = 3 \). Thus, \( \sqrt[3]{54} = 3 \sqrt[3]{2} \).

Example 2: Simplifying a Fourth Root

Simplify: \( \sqrt[4]{80} \)

1. Identify the index: 4.
2. Find the largest perfect fourth power factor of 80. Here, \( 16 \) is the largest perfect fourth power factor.
3. Rewrite the radicand: \( 80 = 16 \times 5 \).
4. Apply the product property: \( \sqrt[4]{80} = \sqrt[4]{16 \times 5} = \sqrt[4]{16} \times \sqrt[4]{5} \).
5. Simplify: \( \sqrt[4]{16} = 2 \). Thus, \( \sqrt[4]{80} = 2 \sqrt[4]{5} \).

By following these steps, you can simplify higher-order roots systematically and accurately.

In this section, you will find a variety of examples and practice problems to help you master simplifying radical expressions. Work through these step-by-step to ensure you understand each concept.

Example 1: Simplifying a Square Root

Given the expression \( \sqrt{50} \), simplify it.

1. Find the prime factorization of 50: \( 50 = 2 \times 5^2 \).
2. Rewrite the square root using the prime factors: \( \sqrt{50} = \sqrt{2 \times 5^2} \).
3. Apply the property of square roots: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
4. Simplify: \( \sqrt{50} = \sqrt{2} \times \sqrt{5^2} = \sqrt{2} \times 5 = 5\sqrt{2} \).

Example 2: Combining Like Radicals

Simplify \( 3\sqrt{18} + 2\sqrt{8} \).

1. Simplify each radical:
   • \( \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \)
   • \( \sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2} \)
2. Rewrite the expression with simplified radicals: \( 3\sqrt{18} + 2\sqrt{8} = 3(3\sqrt{2}) + 2(2\sqrt{2}) \).
3. Combine like terms: \( 9\sqrt{2} + 4\sqrt{2} = (9 + 4)\sqrt{2} = 13\sqrt{2} \).

Example 3: Rationalizing the Denominator

Simplify \( \frac{5}{\sqrt{3}} \) by rationalizing the denominator.

1. Multiply the numerator and the denominator by \( \sqrt{3} \): \( \frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \).
2. Simplify: \( \frac{5\sqrt{3}}{3} \).

Practice Problems

1. Simplify \( \sqrt{72} \).
2. Simplify \( 4\sqrt{45} - 2\sqrt{20} \).
3. Rationalize the denominator of \( \frac{7}{\sqrt{5}} \).
4. Combine like radicals: \( 2\sqrt{50} + 3\sqrt{18} \).
5. Simplify \( \sqrt[3]{81} \).

Answers to Practice Problems

1. \( 6\sqrt{2} \)
2. \( 6\sqrt{5} - 4\sqrt{5} = 2\sqrt{5} \)
3. \( \frac{7\sqrt{5}}{5} \)
4. \( 10\sqrt{2} + 9\sqrt{2} = 19\sqrt{2} \)
5. \( 3\sqrt[3]{3} \)

Here you can find a variety of resources and worksheets to help reinforce your understanding of simplifying radical expressions. These materials are designed to provide additional practice and support for students at various levels.

• Worksheets for Simplifying Radical Expressions:
• Online Practice and Tutorials:
• Video Lessons:

These resources will provide you with a comprehensive set of tools to master simplifying radical expressions. Whether you prefer printable worksheets, interactive online practice, or video lessons, you'll find what you need to succeed.