Topic simplify square root 20: Understanding how to simplify the square root of 20 can be a valuable skill in math. This guide will walk you through various methods to simplify √20, including prime factorization and the long division method. By mastering these techniques, you’ll be able to simplify any square root with confidence.
Table of Content
- Simplify Square Root of 20
- Introduction to Square Roots
- Understanding Square Roots
- What is the Square Root of 20?
- Methods to Simplify the Square Root of 20
- Step-by-Step Simplification Process
- Example Problems
- Using the Properties of Square Roots
- Combining Square Roots
- Common Mistakes to Avoid
- Practical Applications of Simplifying Square Roots
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai của 20. Video này sẽ giúp bạn hiểu rõ hơn về quy trình và các bước để tính toán.
Simplify Square Root of 20
The square root of 20, represented as \(\sqrt{20}\), can be simplified using the following steps:
Step-by-Step Simplification
-
List the factors of 20:
\(1, 2, 4, 5, 10, 20\) -
Identify the perfect squares from the list of factors:
\(1, 4\) -
Divide 20 by the largest perfect square:
\(20 / 4 = 5\) -
Calculate the square root of the largest perfect square:
\(\sqrt{4} = 2\) -
Combine the results to get the simplest form:
\(\sqrt{20} = 2\sqrt{5}\)
Explanation
We simplify the square root of 20 by factoring it into a product of perfect squares and other integers. The largest perfect square factor of 20 is 4, which simplifies the expression. By taking the square root of 4, we can then express the square root of 20 in its simplest radical form as \(2\sqrt{5}\).
Alternative Method: Long Division
The long division method can also be used to find the value of \(\sqrt{20}\), which approximates to 4.472. This method provides an accurate decimal value and is especially useful when perfect square factors are not easily identified.
Conclusion
By understanding the steps to simplify the square root of 20, we can apply these techniques to other non-perfect square roots, enhancing our problem-solving skills in algebra.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics and is used to determine a number that, when multiplied by itself, results in the original number. The square root is represented by the radical sign (√). For example, the square root of 9 is 3, because 3 × 3 = 9. Understanding square roots helps in simplifying complex equations and is crucial in various fields of science and engineering.
In mathematical terms, the square root of a number x is a number y such that y2 = x. For non-negative x, this is usually written as:
\[\sqrt{x}\]
Square roots have several important properties:
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
These properties are often used to simplify expressions involving square roots. For example, \(\sqrt{20}\) can be simplified by breaking it down into its prime factors and using these properties to simplify the expression further.
Understanding Square Roots
Square roots are a fundamental concept in mathematics that involve finding a number which, when multiplied by itself, yields the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \). For example, the square root of 16 is 4, because \( 4 \times 4 = 16 \).
Here are some key points to understand about square roots:
- Notation: The square root of a number \( x \) is written as \( \sqrt{x} \). If \( y \) is the square root of \( x \), then \( y^2 = x \).
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For example, both 3 and -3 are square roots of 9 because \( 3^2 = 9 \) and \( (-3)^2 = 9 \). However, by convention, the square root symbol \( \sqrt{} \) refers to the positive root.
- Perfect Squares: If the square root of a number is an integer, the number is called a perfect square. Examples of perfect squares include 1, 4, 9, 16, and 25.
- Irrational Numbers: Some square roots are irrational numbers, meaning they cannot be expressed as a simple fraction. For instance, \( \sqrt{2} \) and \( \sqrt{3} \) are irrational.
To better grasp the concept, let's look at the square roots of some common numbers:
| Number | Square Root |
|---|---|
| 1 | \( \sqrt{1} = 1 \) |
| 4 | \( \sqrt{4} = 2 \) |
| 9 | \( \sqrt{9} = 3 \) |
| 16 | \( \sqrt{16} = 4 \) |
| 25 | \( \sqrt{25} = 5 \) |
Understanding square roots is crucial for simplifying them. In the next section, we will explore the specific case of the square root of 20.
What is the Square Root of 20?
The square root of 20 is denoted as and can be simplified to . Here’s how we simplify it:
- The prime factorization of 20 is . This means 20 can be written as 4 × 5, where 4 is a perfect square.
- We can separate the square root of the product into the product of the square roots: .
- The square root of 4 is 2, so we can simplify this to .
Thus, the simplest radical form of the square root of 20 is . In decimal form, it is approximately 4.472.
Here is a step-by-step process to understand this simplification better:
- List the factors of 20: 1, 2, 4, 5, 10, 20.
- Identify the perfect squares from the list of factors: 1, 4.
- Divide 20 by the largest perfect square: 20 ÷ 4 = 5.
- Calculate the square root of the largest perfect square: √4 = 2.
- Combine the results to get the simplest form: √20 = 2√5.
To ensure complete understanding, it’s also important to know that the square root of 20 is an irrational number because it cannot be expressed as a simple fraction, due to √5 being irrational.
Another method to find the square root of 20 is by using the long division method, which is more precise and helpful for obtaining decimal values. Here are the steps for the long division method:
- Pair the digits of 20 from right to left: (20).
- Find the largest number whose square is less than or equal to 20 (which is 4, since 4×4 = 16).
- Subtract 16 from 20 to get 4. Bring down pairs of zeros (00) to get 400.
- Double the quotient (4) to get 8. Use 8 as the new divisor to get the next digit (4), as 84 × 4 = 336.
- Repeat the process to get a more accurate value: √20 ≈ 4.472135.
Understanding and practicing these methods will make it easier to simplify square roots and solve related problems efficiently.
Methods to Simplify the Square Root of 20
There are two primary methods to simplify the square root of 20: the Prime Factorization Method and the Long Division Method. Below, we will explore each method step-by-step.
Prime Factorization Method
- Start with the number 20.
- Find the prime factors of 20:
- 20 = 2 × 2 × 5
- Group the prime factors into pairs:
- (2 × 2) and 5
- Take the square root of each pair and simplify:
- √(2 × 2 × 5) = √(4 × 5) = √4 × √5 = 2√5
- The simplified form of √20 is:
- \[ \sqrt{20} = 2\sqrt{5} \]
Long Division Method
The Long Division Method is a systematic approach to find the square root of a number to a desired degree of accuracy. Here’s how to apply it to √20:
- Write the number 20 and set up the long division format.
- Find the largest number whose square is less than or equal to 20. This number is 4 (since 4² = 16).
- Subtract 16 from 20 to get the remainder 4. Bring down a pair of zeros to make it 400.
- Double the divisor (which was 4) to get 8. Determine how many times 80 (ignoring the zero) can be multiplied to stay within 400. The answer is 5 (since 85 × 5 = 425).
- Continue this process to get more decimal places as needed.
- The result for √20 is approximately 4.472135955.
Thus, the square root of 20 can be simplified to 2√5 using the Prime Factorization Method or approximated as 4.4721 using the Long Division Method.

Step-by-Step Simplification Process
The square root of 20 can be simplified using various methods. Here, we will use the Prime Factorization Method to simplify √20. Follow these steps:
-
Factorize 20: Find the prime factors of 20. The prime factorization of 20 is:
\(20 = 2 \times 2 \times 5\)
-
Group the Factors: Group the prime factors into pairs of identical factors:
\(20 = (2 \times 2) \times 5\)
-
Simplify the Radicals: Take one factor from each pair out of the square root:
\(\sqrt{20} = \sqrt{(2 \times 2) \times 5} = 2 \sqrt{5}\)
So, the simplified form of the square root of 20 is \(2\sqrt{5}\).
Let's break down this process with additional steps to ensure complete understanding:
-
Identify Perfect Squares: List the factors of 20 and identify the perfect squares:
Factors: 1, 2, 4, 5, 10, 20
Perfect squares: 1, 4
-
Divide by the Largest Perfect Square: Divide 20 by the largest perfect square identified (which is 4):
\(20 \div 4 = 5\)
-
Calculate the Square Root: Calculate the square root of the perfect square (4):
\(\sqrt{4} = 2\)
-
Combine the Results: Combine the results to get the simplest radical form:
\(\sqrt{20} = 2\sqrt{5}\)
This method ensures that the square root is simplified correctly and efficiently. By following these steps, you can simplify any square root by finding its prime factors, grouping them, and simplifying the radicals.
Example Problems
Here are a few example problems to help illustrate the process of simplifying square roots. We'll go through the steps for each example.
Example 1: √20
To simplify √20:
- Factorize 20 into its prime factors: \(20 = 2 \times 2 \times 5\).
- Group the pairs of prime factors: \(\sqrt{20} = \sqrt{2^2 \times 5}\).
- Take the square root of the perfect squares: \(\sqrt{2^2 \times 5} = 2\sqrt{5}\).
- Thus, \(\sqrt{20} = 2\sqrt{5}\).
Example 2: √45
To simplify √45:
- Factorize 45 into its prime factors: \(45 = 3 \times 3 \times 5\).
- Group the pairs of prime factors: \(\sqrt{45} = \sqrt{3^2 \times 5}\).
- Take the square root of the perfect squares: \(\sqrt{3^2 \times 5} = 3\sqrt{5}\).
- Thus, \(\sqrt{45} = 3\sqrt{5}\).
Example 3: √12
To simplify √12:
- Factorize 12 into its prime factors: \(12 = 2 \times 2 \times 3\).
- Group the pairs of prime factors: \(\sqrt{12} = \sqrt{2^2 \times 3}\).
- Take the square root of the perfect squares: \(\sqrt{2^2 \times 3} = 2\sqrt{3}\).
- Thus, \(\sqrt{12} = 2\sqrt{3}\).
Example 4: √50
To simplify √50:
- Factorize 50 into its prime factors: \(50 = 2 \times 5 \times 5\).
- Group the pairs of prime factors: \(\sqrt{50} = \sqrt{2 \times 5^2}\).
- Take the square root of the perfect squares: \(\sqrt{2 \times 5^2} = 5\sqrt{2}\).
- Thus, \(\sqrt{50} = 5\sqrt{2}\).
Example 5: √75
To simplify √75:
- Factorize 75 into its prime factors: \(75 = 3 \times 5 \times 5\).
- Group the pairs of prime factors: \(\sqrt{75} = \sqrt{3 \times 5^2}\).
- Take the square root of the perfect squares: \(\sqrt{3 \times 5^2} = 5\sqrt{3}\).
- Thus, \(\sqrt{75} = 5\sqrt{3}\).
Example 6: √98
To simplify √98:
- Factorize 98 into its prime factors: \(98 = 2 \times 7 \times 7\).
- Group the pairs of prime factors: \(\sqrt{98} = \sqrt{2 \times 7^2}\).
- Take the square root of the perfect squares: \(\sqrt{2 \times 7^2} = 7\sqrt{2}\).
- Thus, \(\sqrt{98} = 7\sqrt{2}\).
Using the Properties of Square Roots
The properties of square roots are fundamental tools that can simplify complex radical expressions. These properties include the product rule, the quotient rule, and recognizing perfect squares. Let's explore these properties and how they can be used in practice.
Product Rule
The product rule states that the square root of a product is equal to the product of the square roots of the factors. Mathematically, this is expressed as:
\[\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\]
For example, to simplify \(\sqrt{20}\) using the product rule:
- Factor the radicand into its prime factors: \(20 = 4 \times 5\).
- Apply the product rule: \(\sqrt{20} = \sqrt{4 \times 5} = \sqrt{4} \cdot \sqrt{5}\).
- Simplify the square roots: \(\sqrt{4} = 2\), so \(\sqrt{20} = 2\sqrt{5}\).
Quotient Rule
The quotient rule states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. This is represented as:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
For example, to simplify \(\sqrt{\frac{25}{9}}\):
- Apply the quotient rule: \(\sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}}\).
- Simplify the square roots: \(\sqrt{25} = 5\) and \(\sqrt{9} = 3\), so \(\sqrt{\frac{25}{9}} = \frac{5}{3}\).
Recognizing Perfect Squares
Recognizing and factoring out perfect squares from under the radical can greatly simplify the expression. A perfect square is a number that has an integer as its square root (e.g., 1, 4, 9, 16).
For example, to simplify \(\sqrt{50}\):
- Factor the radicand: \(50 = 25 \times 2\).
- Apply the product rule: \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \cdot \sqrt{2}\).
- Simplify the square roots: \(\sqrt{25} = 5\), so \(\sqrt{50} = 5\sqrt{2}\).
Combining Multiple Square Roots
When dealing with the product of multiple square roots, you can combine them into a single square root using the product rule, and then simplify:
For example, to simplify \(\sqrt{12} \cdot \sqrt{3}\):
- Combine the radicals: \(\sqrt{12} \cdot \sqrt{3} = \sqrt{12 \times 3} = \sqrt{36}\).
- Simplify: \(\sqrt{36} = 6\).
These properties make it easier to handle and simplify square root expressions, leading to more manageable and comprehensible results.
Combining Square Roots
Combining square roots involves using specific properties and rules to simplify expressions that contain multiple square root terms. Here are some key methods and examples to guide you:
Addition and Subtraction of Square Roots
To combine square roots through addition or subtraction, the radicals must be like terms, meaning the numbers under the square root must be identical. If they are not, you cannot directly combine them.
- Example 1: Simplify \(3\sqrt{3} + 2\sqrt{3}\)
- Identify the like terms: Both terms have \(\sqrt{3}\).
- Combine the coefficients: \(3 + 2 = 5\).
- The simplified form is: \(5\sqrt{3}\).
- Example 2: Simplify \(3\sqrt{3} + 2\sqrt{5} + \sqrt{3}\)
- Identify the like terms: \(3\sqrt{3}\) and \(\sqrt{3}\) are like terms.
- Combine the coefficients of like terms: \(3 + 1 = 4\).
- The simplified form is: \(4\sqrt{3} + 2\sqrt{5}\).
Multiplication of Square Roots
When multiplying square roots, you can combine them under a single radical if they have no coefficients or if they can be simplified.
- Example: Simplify \(\sqrt{2} \times \sqrt{8}\)
- Combine the numbers under a single radical: \(\sqrt{2 \times 8} = \sqrt{16}\).
- Simplify the result: \(\sqrt{16} = 4\).
Division of Square Roots
You can also divide square roots by combining the numbers under a single radical and then simplifying.
- Example: Simplify \(\frac{\sqrt{50}}{\sqrt{2}}\)
- Combine under a single radical: \(\sqrt{\frac{50}{2}} = \sqrt{25}\).
- Simplify the result: \(\sqrt{25} = 5\).
Combining Multiple Radicals
In more complex expressions, you can factor and simplify radicals before combining them.
- Example: Simplify \(\sqrt{18} - 2\sqrt{8}\)
- Simplify each radical term: \(\sqrt{18} = 3\sqrt{2}\) and \(2\sqrt{8} = 4\sqrt{2}\).
- Combine like terms: \(3\sqrt{2} - 4\sqrt{2} = -\sqrt{2}\).
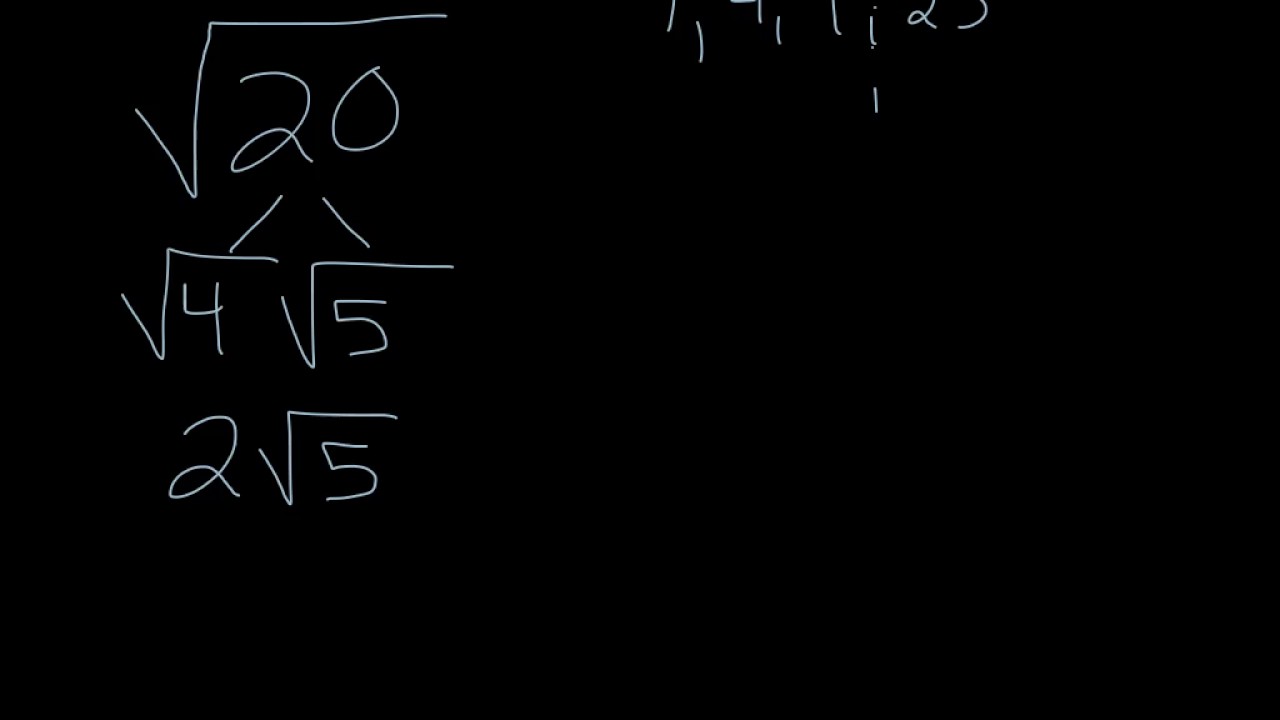
Common Mistakes to Avoid
When simplifying the square root of 20, students often encounter several common pitfalls. Being aware of these mistakes can help ensure accurate and efficient calculations. Here are some of the most frequent errors and tips on how to avoid them:
- Forgetting to Check for Perfect Squares:
One of the most common mistakes is not recognizing that 20 can be broken down into smaller perfect squares. Always look for perfect square factors to simplify the radical. For example, since 20 = 4 × 5 and √4 = 2, we have:
\[
\sqrt{20} = \sqrt{4 \times 5} = \sqrt{4} \times \sqrt{5} = 2\sqrt{5}
\] - Incorrect Factorization:
Another mistake is incorrectly factoring the number inside the square root. Ensure that you correctly identify the prime factors. For instance:
\[
20 = 2^2 \times 5
\]This can then be simplified to:
\[
\sqrt{20} = \sqrt{2^2 \times 5} = 2\sqrt{5}
\] - Rushing Through Steps:
Rushing through the simplification process can lead to errors. Take your time to carefully break down each step. Simplifying square roots is a process that requires patience and attention to detail.
- Not Simplifying Completely:
Ensure that you simplify the square root completely. Sometimes students stop too early and do not simplify the expression as much as possible. Always check your work to make sure every factor has been accounted for and simplified appropriately.
- Misapplying Square Root Properties:
It's important to apply the properties of square roots correctly. For example, the property \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\) is useful, but ensure you apply it correctly. Misapplication can lead to incorrect results.
By avoiding these common mistakes, you can simplify the square root of 20 (and other numbers) more accurately and efficiently. Remember, practice makes perfect, so keep practicing different examples to become more confident in your skills!
Practical Applications of Simplifying Square Roots
Simplifying square roots is a useful skill with various practical applications in different fields. Understanding these applications can enhance your appreciation of the importance of this mathematical process. Here are some key areas where simplified square roots are applied:
-
Finance:
In finance, square roots are used to calculate stock market volatility, which measures the degree of variation in a stock's price over time. This calculation involves taking the square root of the variance of a stock’s returns, helping investors assess the risk associated with an investment.
-
Architecture and Engineering:
Architects and engineers use square roots to determine the natural frequency of structures like bridges and buildings. The natural frequency helps predict how a structure will respond to various loads, such as wind or traffic. Simplified square roots make these calculations more manageable.
-
Physics:
Square roots are often used in physics to determine quantities such as the velocity of an object, the intensity of sound waves, or the energy levels in quantum mechanics. For instance, the time it takes for an object to fall to the ground can be found using the formula \( t = \frac{\sqrt{h}}{4} \), where \( h \) is the height from which the object is dropped.
-
Statistics:
In statistics, square roots are used to compute standard deviation, a measure of the amount of variation or dispersion in a set of values. The standard deviation is the square root of the variance, which provides insights into data distribution.
-
Geometry:
Geometry frequently employs square roots to solve problems involving right triangles and other polygons. For example, the Pythagorean theorem involves calculating the length of a side of a triangle by taking the square root of the sum of the squares of the other two sides.
-
Computer Science:
In computer programming, square roots are used in algorithms for encryption, image processing, and game physics. These applications often require precise calculations that involve simplified square roots.
These are just a few examples of how simplifying square roots can be applied in real-world scenarios. Mastering this skill can be highly beneficial across various disciplines, enhancing problem-solving abilities and contributing to more efficient and accurate calculations.
Hướng dẫn cách đơn giản hóa căn bậc hai của 20. Video này sẽ giúp bạn hiểu rõ hơn về quy trình và các bước để tính toán.
Cách Đơn Giản Hóa Căn Bậc Hai của 20: Sqrt(20)
READ MORE:
Hướng dẫn đơn giản hóa căn bậc hai trong Đại Số 2, chuẩn bị cho số ảo, với các ví dụ căn(9) và căn(20).
Đại Số 2 - Đơn Giản Hóa Căn Bậc Hai để Chuẩn Bị cho Số Ảo, Căn(9), Căn(20)




