Topic root x squared: Welcome to our comprehensive guide on Root x Squared! This article will help you understand the fundamentals, properties, and practical applications of square roots and x squared. Whether you're a student or just curious about mathematics, we've got you covered with clear explanations and examples. Dive in to master Root x Squared effortlessly!
Table of Content
- Understanding the Square Root of x Squared
- Introduction to Square Roots
- Understanding x Squared
- Properties of Square Roots
- Simplifying Square Roots
- Square Roots in Algebra
- Square Root of x Squared
- Examples and Applications
- Common Mistakes and Misconceptions
- Advanced Topics
- Practical Applications of Square Roots
- YOUTUBE: Video giải thích về gốc của x-bình phương và tại sao 90% học sinh trả lời sai câu hỏi này. Xem ngay để hiểu rõ hơn và tránh những lỗi phổ biến.
Understanding the Square Root of x Squared
The concept of the square root of x squared is an interesting topic in mathematics, particularly in algebra. When we calculate the square root of \(x^2\), we essentially undo the squaring operation.
Basic Definition
The square root of \(x^2\) is given by:
\[\sqrt{x^2} = |x|\]
This means that the square root of \(x^2\) is the absolute value of x. This is because both positive and negative values of x, when squared, result in the same positive value.
Examples and Properties
- If \(x = 5\), then \(\sqrt{x^2} = \sqrt{25} = 5\).
- If \(x = -5\), then \(\sqrt{x^2} = \sqrt{25} = 5\).
In both cases, the square root of \(x^2\) results in the positive value of x.
Principal Square Root
When we refer to \(\sqrt{x^2}\), we usually mean the principal (or positive) square root:
\[\sqrt{25} = 5\]
However, it is important to note that the equation \(x^2 = 25\) has two solutions:
\[x = 5 \quad \text{and} \quad x = -5\]
Thus, the equation \(\sqrt{x^2} = x\) holds true for non-negative values of x, but for all real values of x, we use \(|x|\).
Why Use Absolute Value?
The absolute value ensures we capture both possible roots. The definition:
\[\sqrt{x^2} = |x|\]
is precise because \(|x|\) is always non-negative, regardless of whether x is positive or negative.
Mathematical Proof
To illustrate why \(\sqrt{x^2} = |x|\), consider the following steps:
- Start with \(y = \sqrt{x^2}\).
- Square both sides to get \(y^2 = x^2\).
- Thus, \(y = |x|\) to satisfy both positive and negative roots of \(x^2\).
Application in Solving Equations
When solving equations involving squares, it's crucial to remember both potential roots. For example, solving \(x^2 = 9\) involves:
- Taking the square root of both sides: \(\sqrt{x^2} = \sqrt{9}\).
- Thus, \(|x| = 3\), leading to \(x = 3\) or \(x = -3\).
Conclusion
Understanding the square root of \(x^2\) is essential for solving quadratic equations and simplifying expressions in algebra. Remember, the absolute value function ensures we capture the principal (non-negative) root, which is crucial for accurate mathematical solutions.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because 4 × 4 = 16. Square roots are fundamental in mathematics and are denoted by the radical symbol √.
Here's a step-by-step introduction to understanding square roots:
- Identify the number you want to find the square root of, known as the radicand.
- Determine if the number is a perfect square (a number whose square root is an integer).
- If the number is a perfect square, find its square root. For example, √25 = 5.
- If the number is not a perfect square, approximate the square root using methods such as the prime factorization or long division method.
Examples:
- √9 = 3 (since 3 × 3 = 9)
- √36 = 6 (since 6 × 6 = 36)
- √2 ≈ 1.414 (since 1.414 × 1.414 ≈ 2)
Properties of Square Roots:
- Non-Negative Results: The square root of a non-negative number is always non-negative.
- Product Property: The square root of a product is the product of the square roots, i.e., √(a * b) = √a * √b.
- Quotient Property: The square root of a quotient is the quotient of the square roots, i.e., √(a / b) = √a / √b.
- Power of 2: The square root of x squared is the absolute value of x, i.e., √(x^2) = |x|.
Understanding and simplifying square roots is crucial for solving various mathematical problems and for applications in algebra, geometry, and beyond. In the following sections, we will delve deeper into the properties and applications of square roots.
Understanding x Squared
In mathematics, "x squared" refers to a number multiplied by itself. It is written as \(x^2\), which means \(x \times x\). Squaring a number is a fundamental concept that appears frequently in algebra and other areas of mathematics.
Here are some important points to understand about \(x^2\):
- Definition: For any real number \(x\), \(x^2 = x \times x\). For example, if \(x = 3\), then \(3^2 = 3 \times 3 = 9\).
- Properties:
- \(x^2\) is always non-negative. This means that \(x^2 \geq 0\) for all real numbers \(x\).
- The square of a positive number is positive, and the square of a negative number is also positive. For instance, \((-2)^2 = 4\).
- \(x^2\) is a parabolic function, meaning its graph forms a parabola opening upwards.
- Applications: Squaring numbers is used in various mathematical problems and real-world applications, such as calculating areas of squares and solving quadratic equations.
To further illustrate, let's look at a few examples:
- If \(x = 5\), then \(x^2 = 5^2 = 25\).
- If \(x = -7\), then \(x^2 = (-7)^2 = 49\).
- If \(x = 0\), then \(x^2 = 0^2 = 0\).
Understanding \(x^2\) is crucial for progressing in algebra and other higher-level mathematics. The concept of squaring extends to functions, where the square of a function is defined pointwise: if \(f(x)\) is a function, then \((f(x))^2 = f(x) \times f(x)\).
Here's a table summarizing the squares of some common numbers:
| x | \(x^2\) |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
By understanding and mastering the concept of \(x^2\), students can develop a strong foundation for more complex mathematical topics and real-world problem-solving skills.
Properties of Square Roots
Square roots are fundamental in mathematics and possess several important properties that are useful in various calculations and problem-solving scenarios. The square root of a number \(x\) is denoted as \(\sqrt{x}\), and it is a value that, when multiplied by itself, gives \(x\). For example, \(\sqrt{9} = 3\) because \(3 \times 3 = 9\).
Here are the key properties of square roots:
- Non-negative Results: The principal square root of a non-negative number \(x\) is always non-negative. For example, \(\sqrt{16} = 4\), not \(-4\).
- Product Property: The square root of a product is the product of the square roots. Mathematically, \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\). For example, \(\sqrt{36} = \sqrt{9 \times 4} = \sqrt{9} \times \sqrt{4} = 3 \times 2 = 6\).
- Quotient Property: The square root of a quotient is the quotient of the square roots. This is written as \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) for \(b \neq 0\). For example, \(\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} = 2.5\).
- Square of a Square Root: The square of a square root returns the original number: \((\sqrt{x})^2 = x\). For example, \((\sqrt{5})^2 = 5\).
- Addition and Subtraction: Square roots do not distribute over addition or subtraction. In general, \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\) and \(\sqrt{a - b} \neq \sqrt{a} - \sqrt{b}\). For example, \(\sqrt{4 + 9} = \sqrt{13} \neq \sqrt{4} + \sqrt{9} = 2 + 3 = 5\).
To further illustrate these properties, consider the following examples:
- \(\sqrt{49} = 7\), because \(7 \times 7 = 49\).
- \(\sqrt{64} = 8\), because \(8 \times 8 = 64\).
- \(\sqrt{4 \times 9} = \sqrt{36} = 6\), which is the same as \(\sqrt{4} \times \sqrt{9} = 2 \times 3 = 6\).
- \(\sqrt{\frac{16}{25}} = \frac{\sqrt{16}}{\sqrt{25}} = \frac{4}{5} = 0.8\).
Understanding these properties of square roots is crucial for solving algebraic equations, simplifying expressions, and tackling more complex mathematical problems. Here's a table summarizing the square roots of some common perfect squares:
| x | \(\sqrt{x}\) |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
By mastering these properties, students can gain a deeper understanding of how square roots function and apply this knowledge to a variety of mathematical contexts.
Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest form. This process often requires factoring the number under the square root sign into its prime factors and then simplifying. Here is a step-by-step guide to simplifying square roots:
- Identify Perfect Squares: Determine if the number under the square root sign (\(n\)) is a perfect square. If \(n\) is a perfect square, its square root is an integer. For example, \(\sqrt{36} = 6\) because \(36 = 6 \times 6\).
- Factorize the Number: If \(n\) is not a perfect square, factorize it into its prime factors. For example, for \(\sqrt{72}\), we write \(72 = 2^3 \times 3^2\).
- Group the Factors: Group the factors into pairs of identical numbers. Each pair of identical factors can be taken out of the square root as a single number. For example, in \(\sqrt{72} = \sqrt{2^3 \times 3^2}\), we can group the factors as \((2^2 \times 3^2) \times 2 = 4 \times 9 \times 2\).
- Simplify: Simplify the square root by taking out the pairs. For \(\sqrt{72}\), this gives us \(\sqrt{4 \times 9 \times 2} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6 \sqrt{2}\).
Here are some examples to illustrate the process:
- \(\sqrt{50}\):
- Factorize 50: \(50 = 2 \times 5^2\).
- Identify pairs: \(5^2\) is a pair.
- Simplify: \(\sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2}\).
- \(\sqrt{18}\):
- Factorize 18: \(18 = 2 \times 3^2\).
- Identify pairs: \(3^2\) is a pair.
- Simplify: \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\).
Understanding and applying these steps will help in simplifying any square root expression. Let's summarize some common square roots in a table:
| Expression | Simplified Form |
|---|---|
| \(\sqrt{8}\) | \(2\sqrt{2}\) |
| \(\sqrt{12}\) | \(2\sqrt{3}\) |
| \(\sqrt{20}\) | \(2\sqrt{5}\) |
| \(\sqrt{45}\) | \(3\sqrt{5}\) |
| \(\sqrt{75}\) | \(5\sqrt{3}\) |
By practicing these steps, students can simplify square roots more effectively, which is a valuable skill in algebra and beyond.

Square Roots in Algebra
Square roots play a crucial role in algebra, appearing in various equations, expressions, and problem-solving scenarios. Understanding how to manipulate and simplify square roots is essential for mastering algebraic concepts. Here is a detailed look at how square roots are used in algebra:
Solving Quadratic Equations
Square roots are often used to solve quadratic equations of the form \(ax^2 + bx + c = 0\). One common method is completing the square, which involves rewriting the equation so that one side is a perfect square trinomial. Another method is the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
This formula directly involves square roots, where the expression under the square root, \(b^2 - 4ac\), is called the discriminant.
Radical Expressions
Square roots appear in radical expressions, which are expressions that contain roots. Simplifying radical expressions involves combining like terms and reducing the expression to its simplest form. For example:
\[
\sqrt{50} + \sqrt{18} = 5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}
\]
Rationalizing the Denominator
In algebra, it is often useful to eliminate square roots from the denominator of a fraction. This process is called rationalizing the denominator. For example:
\[
\frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
Solving Radical Equations
Equations that contain square roots are known as radical equations. To solve these, isolate the radical on one side of the equation and then square both sides to eliminate the square root. For example:
\[
\sqrt{x + 3} = 5
\]
First, square both sides:
\[
x + 3 = 25
\]
Then solve for \(x\):
\[
x = 22
\]
Examples and Practice Problems
Here are some practice problems to help solidify your understanding of square roots in algebra:
- Solve the quadratic equation \(x^2 - 4x - 5 = 0\) using the quadratic formula.
- Simplify the radical expression \(\sqrt{72} + \sqrt{18}\).
- Rationalize the denominator of \(\frac{5}{\sqrt{3}}\).
- Solve the radical equation \(\sqrt{2x + 1} = 3\).
Summary Table
The table below summarizes key concepts involving square roots in algebra:
| Concept | Example | Explanation |
|---|---|---|
| Quadratic Formula | \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) | Used to find the roots of a quadratic equation. |
| Radical Expression | \(\sqrt{50} + \sqrt{18}\) | Simplify by combining like terms. |
| Rationalizing the Denominator | \(\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\) | Eliminate square roots from the denominator. |
| Solving Radical Equations | \(\sqrt{x + 3} = 5\) | Isolate the radical and square both sides to solve. |
By understanding and practicing these concepts, students can gain a deeper mastery of algebra and effectively utilize square roots in various mathematical contexts.
Square Root of x Squared
The square root of \(x\) squared, written as \(\sqrt{x^2}\), is a fundamental concept in algebra with significant implications in various mathematical problems. Understanding how to simplify and interpret \(\sqrt{x^2}\) is crucial for solving equations and working with algebraic expressions.
Definition and Basic Property
The square root of \(x^2\) is given by the absolute value of \(x\), which can be written as:
\[
\sqrt{x^2} = |x|
\]
This is because squaring a number always results in a non-negative value, and the square root function returns the principal (non-negative) root. Therefore, the absolute value ensures that the result is non-negative regardless of the sign of \(x\).
Why Absolute Value?
Consider the following examples to understand why the absolute value is necessary:
- For \(x = 5\):
\[
\sqrt{5^2} = \sqrt{25} = 5
\] - For \(x = -5\):
\[
\sqrt{(-5)^2} = \sqrt{25} = 5
\]
In both cases, the result is 5, which is the absolute value of \(x\). Hence, \(\sqrt{x^2} = |x|\).
Simplifying Expressions
When simplifying expressions involving \(\sqrt{x^2}\), it's important to apply the absolute value to ensure the correct result. For instance:
- Simplify \(\sqrt{(3x)^2}\):
\[
\sqrt{(3x)^2} = |3x| = 3|x|
\] - Simplify \(\sqrt{(2y - 4)^2}\):
\[
\sqrt{(2y - 4)^2} = |2y - 4|
\]
Application in Solving Equations
Understanding \(\sqrt{x^2} = |x|\) is essential when solving equations. Consider the equation:
\[
\sqrt{x^2} = k
\]
Since \(\sqrt{x^2} = |x|\), the equation becomes:
\[
|x| = k
\]
This implies that \(x\) can be either \(k\) or \(-k\). Therefore, the solutions are:
\[
x = k \quad \text{or} \quad x = -k
\]
Examples
Let's look at some examples to solidify the concept:
- Solve \(\sqrt{x^2} = 7\):
\[
|x| = 7 \implies x = 7 \quad \text{or} \quad x = -7
\] - Simplify \(\sqrt{(4x + 1)^2}\):
\[
\sqrt{(4x + 1)^2} = |4x + 1|
\] - Solve \(\sqrt{x^2} = 0\):
\[
|x| = 0 \implies x = 0
\]
Summary Table
The table below summarizes the key points regarding the square root of \(x\) squared:
| Expression | Simplified Form | Explanation |
|---|---|---|
| \(\sqrt{x^2}\) | \(|x|\) | Absolute value of \(x\). |
| \(\sqrt{(3x)^2}\) | \(3|x|\) | Coefficient taken out, absolute value applied. |
| \(\sqrt{(a - b)^2}\) | \(|a - b|\) | Absolute value of the expression. |
By mastering the concept of the square root of \(x\) squared, students can enhance their algebraic skills and confidently solve a variety of mathematical problems.
Examples and Applications
Square roots and their properties are widely used in various mathematical problems and real-world applications. Understanding how to apply square roots in different contexts can greatly enhance problem-solving skills. Here are some detailed examples and applications of square roots:
Example 1: Solving Quadratic Equations
Consider the quadratic equation \(x^2 - 4 = 0\). To solve this equation, follow these steps:
- Isolate the square term:
\[
x^2 = 4
\] - Take the square root of both sides:
\[
\sqrt{x^2} = \sqrt{4}
\] - Apply the property of square roots:
\[
|x| = 2
\] - Determine the solutions:
\[
x = 2 \quad \text{or} \quad x = -2
\]
Example 2: Simplifying Expressions
Simplify the expression \(\sqrt{50} + \sqrt{18}\):
- Factorize each number:
\[
50 = 2 \times 5^2 \quad \text{and} \quad 18 = 2 \times 3^2
\] - Simplify each square root:
\[
\sqrt{50} = 5\sqrt{2} \quad \text{and} \quad \sqrt{18} = 3\sqrt{2}
\] - Combine like terms:
\[
5\sqrt{2} + 3\sqrt{2} = 8\sqrt{2}
\]
Example 3: Distance Formula
The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a coordinate plane is given by the distance formula:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
For points \((3, 4)\) and \((7, 1)\):
- Calculate the differences:
\[
x_2 - x_1 = 7 - 3 = 4 \quad \text{and} \quad y_2 - y_1 = 1 - 4 = -3
\] - Substitute into the distance formula:
\[
d = \sqrt{4^2 + (-3)^2} = \sqrt{16 + 9} = \sqrt{25} = 5
\]
Example 4: Pythagorean Theorem
In a right-angled triangle, the length of the hypotenuse \(c\) can be found using the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]
For a triangle with legs \(a = 6\) and \(b = 8\):
- Substitute the values into the formula:
\[
c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10
\]
Applications
Square roots have numerous applications in various fields:
- Physics: Square roots are used in formulas such as the calculation of root mean square speed of gas molecules and in wave equations.
- Engineering: Square roots are applied in determining material properties, stress analysis, and electrical circuit design.
- Finance: Square roots are used in calculating standard deviation, which measures the volatility or risk of an investment.
- Computer Graphics: Algorithms involving distances and magnitudes often use square roots for rendering and animation.
- Statistics: Square roots are essential in various statistical formulas, including the calculation of variance and standard deviation.
Understanding these examples and applications of square roots can help students see the practical utility of this mathematical concept in both academic and real-world scenarios.
Common Mistakes and Misconceptions
Understanding square roots, particularly in the context of algebra, can sometimes be challenging, leading to common mistakes and misconceptions. Recognizing these errors can help in avoiding them and improving mathematical accuracy. Here are some of the most common mistakes and misconceptions related to square roots:
Mistake 1: Incorrectly Simplifying \(\sqrt{x^2}\)
A common mistake is to assume that \(\sqrt{x^2} = x\). However, the correct simplification is \(\sqrt{x^2} = |x|\). The absolute value is necessary because squaring a number always results in a non-negative value, and the square root function must return a non-negative result.
- Incorrect: \(\sqrt{x^2} = x\)
- Correct: \(\sqrt{x^2} = |x|\)
Mistake 2: Misinterpreting Negative Square Roots
Another common misconception is misunderstanding the notation for negative square roots. The square root of a number \(a\), written as \(\sqrt{a}\), always refers to the principal (non-negative) square root. The negative square root is denoted as \(-\sqrt{a}\).
- Incorrect: \(\sqrt{16} = \pm 4\)
- Correct: \(\sqrt{16} = 4\) and \(-\sqrt{16} = -4\)
Mistake 3: Failing to Rationalize the Denominator
In algebra, it is often necessary to rationalize the denominator of a fraction to eliminate any square roots. Failing to do so can leave an expression in an unsimplified form.
- Incorrect: \(\frac{1}{\sqrt{2}}\)
- Correct: \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
Mistake 4: Incorrect Distribution of Square Roots
Square roots cannot be distributed over addition or subtraction within a radical expression. This mistake leads to incorrect simplifications.
- Incorrect: \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\)
- Correct: \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\)
- Example: \(\sqrt{9 + 16} = \sqrt{25} = 5\) but \(\sqrt{9} + \sqrt{16} = 3 + 4 = 7\)
Mistake 5: Incorrectly Simplifying Products and Quotients
While square roots can be distributed over multiplication and division, care must be taken to apply this correctly.
- Incorrect: \(\sqrt{a \times b} \neq \sqrt{a} \times \sqrt{b}\)
- Correct: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- Example: \(\sqrt{9 \times 4} = \sqrt{36} = 6\) and \(\sqrt{9} \times \sqrt{4} = 3 \times 2 = 6\)
Common Misconceptions
- Misconception: \(\sqrt{a^2 + b^2} = a + b\)
Explanation: This is incorrect because the square root of a sum is not equal to the sum of the square roots. For example, \(\sqrt{9 + 16} = \sqrt{25} = 5\) but \(3 + 4 = 7\).
- Misconception: \(\sqrt{a^2 - b^2} = a - b\)
Explanation: Similar to the above, the square root of a difference is not equal to the difference of the square roots. For example, \(\sqrt{25 - 9} = \sqrt{16} = 4\) but \(5 - 3 = 2\).
Examples to Illustrate Correct Understanding
- Simplify \(\sqrt{(2x)^2}\):
\[
\sqrt{(2x)^2} = |2x| = 2|x|
\] - Rationalize the denominator of \(\frac{3}{\sqrt{5}}\):
\[
\frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5}
\] - Simplify \(\sqrt{a \times b}\) when \(a = 9\) and \(b = 4\):
\[
\sqrt{9 \times 4} = \sqrt{36} = 6 \quad \text{and} \quad \sqrt{9} \times \sqrt{4} = 3 \times 2 = 6
\]
By being aware of these common mistakes and misconceptions, students can approach square roots with greater accuracy and confidence, ensuring their mathematical work is correct and reliable.
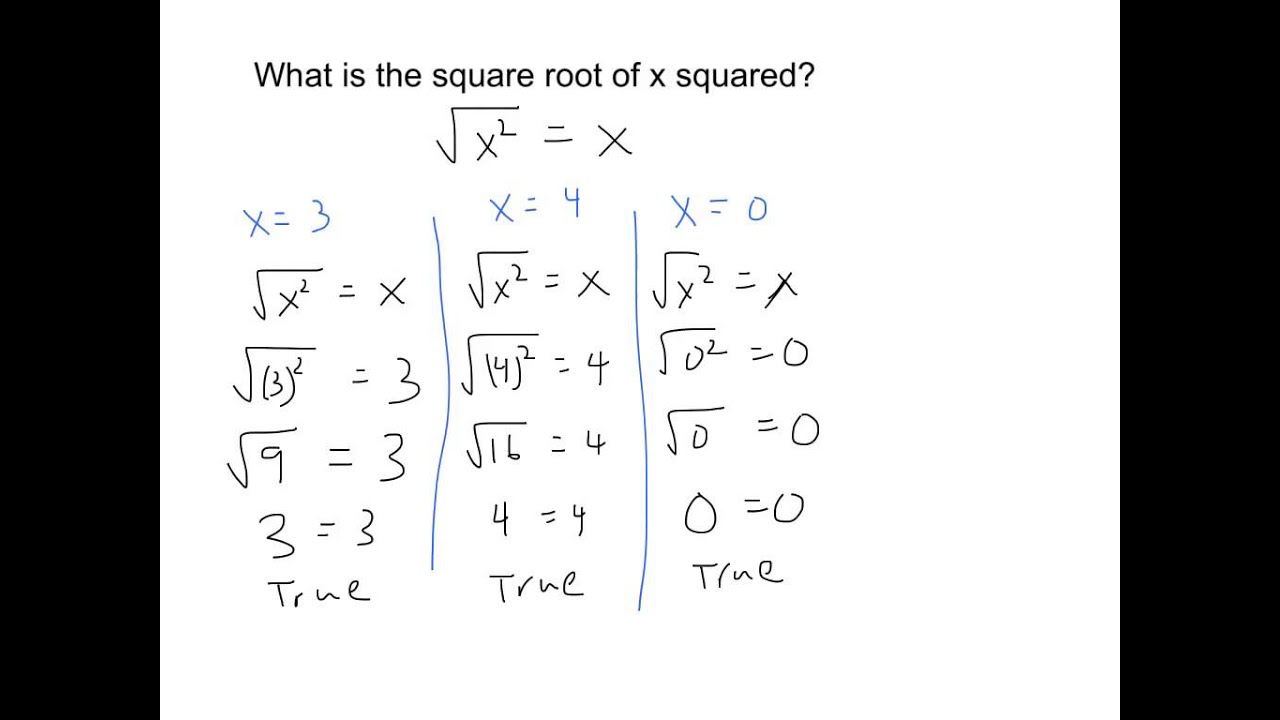
Advanced Topics
Exploring advanced topics related to square roots and \(\sqrt{x^2}\) can deepen your understanding of algebra and its applications in higher mathematics. Here are some advanced concepts that build on the basics of square roots:
Complex Numbers and Square Roots
In real numbers, the square root of a negative number does not exist. However, in the field of complex numbers, it is possible to find the square root of negative numbers. The imaginary unit \(i\) is defined as:
\[
i = \sqrt{-1}
\]
Using this definition, the square root of a negative number can be expressed as:
\[
\sqrt{-a} = \sqrt{a} \cdot i \quad \text{where} \quad a \geq 0
\]
For example:
- \(\sqrt{-4} = \sqrt{4} \cdot i = 2i\)
- \(\sqrt{-9} = \sqrt{9} \cdot i = 3i\)
Square Roots in Higher Dimensions
In vector spaces, the concept of square roots can be extended to norms and distances. For a vector \(\mathbf{v}\) with components \((v_1, v_2, \ldots, v_n)\), the Euclidean norm (or length) is given by:
\[
\|\mathbf{v}\| = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}
\]
This norm represents the distance from the origin to the point defined by \(\mathbf{v}\) in \(n\)-dimensional space.
Applications in Calculus
Square roots frequently appear in calculus, particularly in the context of derivatives and integrals. For example, the derivative of a function involving a square root can be found using the chain rule:
Consider \(f(x) = \sqrt{x}\). The derivative is:
\[
f'(x) = \frac{d}{dx} \left( x^{1/2} \right) = \frac{1}{2} x^{-1/2} = \frac{1}{2\sqrt{x}}
\]
In integration, square roots appear in integrals such as:
\[
\int \sqrt{x} \, dx = \int x^{1/2} \, dx = \frac{2}{3} x^{3/2} + C
\]
Solving Radical Equations
Equations involving square roots can sometimes be challenging to solve. These are known as radical equations. To solve a radical equation, such as \(\sqrt{x + 3} = x - 1\), follow these steps:
- Isolate the square root on one side:
\[
\sqrt{x + 3} = x - 1
\] - Square both sides to eliminate the square root:
\[
(\sqrt{x + 3})^2 = (x - 1)^2 \implies x + 3 = x^2 - 2x + 1
\] - Rearrange the equation to standard quadratic form:
\[
x^2 - 3x - 2 = 0
\] - Factorize and solve the quadratic equation:
\[
(x - 2)(x - 1) = 0 \implies x = 2 \quad \text{or} \quad x = -1
\] - Check for extraneous solutions by substituting back into the original equation. In this case, only \(x = 2\) is valid.
Square Roots in Differential Equations
Square roots can also appear in solutions to differential equations. For instance, consider the differential equation:
\[
\frac{dy}{dx} = \sqrt{1 - y^2}
\]
Separating variables and integrating, we get:
\[
\int \frac{dy}{\sqrt{1 - y^2}} = \int dx
\]
The integral on the left side is the inverse sine function, so the solution is:
\[
\sin^{-1}(y) = x + C \implies y = \sin(x + C)
\]
These advanced topics illustrate the wide-ranging applications and deeper mathematical contexts in which square roots and related concepts play a crucial role. Mastery of these areas can significantly enhance one's mathematical proficiency and problem-solving capabilities.
Practical Applications of Square Roots
Square roots are not just abstract mathematical concepts; they have numerous practical applications in various fields. Understanding how to apply square roots in real-world scenarios can help in solving complex problems efficiently. Here are some practical applications of square roots:
Engineering
In engineering, square roots are used to calculate various parameters, such as stress, strain, and electrical resistance. For example, the stress (\(\sigma\)) in a material subjected to a force (F) can be calculated using the formula:
\[
\sigma = \sqrt{\frac{F}{A}}
\]
where \(A\) is the cross-sectional area of the material.
Physics
Square roots frequently appear in physics equations, particularly in the context of wave motion and quantum mechanics. For example, the speed of a wave (\(v\)) is related to its wavelength (\(\lambda\)) and frequency (\(f\)) by:
\[
v = \lambda f
\]
In quantum mechanics, the wave function is normalized using integrals that involve square roots.
Finance
In finance, the square root is used in the calculation of the standard deviation, which measures the volatility of an investment. The formula for the standard deviation (\(\sigma\)) of a set of values (\(x_i\)) is:
\[
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}
\]
where \(N\) is the number of values and \(\mu\) is the mean of the values.
Medicine
In medicine, the Body Mass Index (BMI) is calculated using the formula:
\[
BMI = \frac{weight}{height^2}
\]
where weight is in kilograms and height is in meters. This formula involves squaring the height, which is the inverse operation of taking the square root.
Computer Science
Square roots are used in computer algorithms, particularly in graphics and simulations. For instance, the Euclidean distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a 2D space is calculated using the square root:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
Architecture
In architecture, square roots are used to calculate dimensions and areas, ensuring structures are proportionally accurate. For example, the diagonal of a rectangle can be found using the Pythagorean theorem:
\[
d = \sqrt{l^2 + w^2}
\]
where \(l\) is the length and \(w\) is the width of the rectangle.
Statistics
Square roots are essential in statistics for various calculations, including the standard error of the mean, confidence intervals, and hypothesis testing. The standard error (\(SE\)) of the mean is given by:
\[
SE = \frac{\sigma}{\sqrt{n}}
\]
where \(\sigma\) is the standard deviation and \(n\) is the sample size.
Astronomy
In astronomy, square roots are used to calculate the luminosity and distance of stars. The inverse square law states that the intensity of light is inversely proportional to the square of the distance from the source:
\[
I = \frac{P}{4 \pi d^2}
\]
where \(I\) is the intensity, \(P\) is the power, and \(d\) is the distance.
These examples illustrate the wide-ranging applications of square roots across various disciplines. Mastering the use of square roots can significantly enhance one's ability to solve practical problems in science, engineering, finance, and beyond.
Video giải thích về gốc của x-bình phương và tại sao 90% học sinh trả lời sai câu hỏi này. Xem ngay để hiểu rõ hơn và tránh những lỗi phổ biến.
Gốc Của X-Bình Phương - Một Câu Hỏi Cơ Bản Được Trả Lời Sai Bởi 90% Học Sinh
READ MORE:
Khám phá căn bậc hai của một số bình phương trong video này để hiểu rõ hơn về khái niệm này và cách tính toán chính xác.
Căn bậc hai của một số bình phương

:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)