Topic what are square numbers in maths: What are square numbers in maths? Discover the fundamentals of square numbers, also known as perfect squares, and how they are formed by multiplying integers by themselves. This article explores their properties, applications, and significance in various fields, providing a clear and engaging introduction to this essential mathematical concept.
Table of Content
- Square Numbers in Mathematics
- Introduction to Square Numbers
- Definition and Basic Concept
- Visual Representation of Square Numbers
- Geometric Applications
- Algebraic Applications
- Number Theory Applications
- Computer Science Applications
- Methods to Identify Square Numbers
- Historical Context and Significance
- Difference Between Consecutive Square Numbers
- Patterns in Square Numbers
- Square Numbers in Real Life
- Square Roots and Their Relationship to Square Numbers
- Perfect Squares vs. Imperfect Squares
- Exercises and Practice Problems
- Common Misconceptions About Square Numbers
- Conclusion
- YOUTUBE:
Square Numbers in Mathematics
Square numbers, also known as perfect squares, are integers that can be expressed as the product of an integer with itself. In other words, a number \( n \) is a square number if there exists an integer \( k \) such that:
\[
n = k^2
\]
Examples of Square Numbers
- 1 (\(1^2 = 1\))
- 4 (\(2^2 = 4\))
- 9 (\(3^2 = 9\))
- 16 (\(4^2 = 16\))
- 25 (\(5^2 = 25\))
- 36 (\(6^2 = 36\))
- 49 (\(7^2 = 49\))
- 64 (\(8^2 = 64\))
- 81 (\(9^2 = 81\))
- 100 (\(10^2 = 100\))
Properties of Square Numbers
- Square numbers are always non-negative.
- The square of an even number is even, and the square of an odd number is odd.
- Square numbers end in 0, 1, 4, 5, 6, or 9 in the decimal system.
- The difference between consecutive square numbers increases linearly. For example, \(4 - 1 = 3\), \(9 - 4 = 5\), \(16 - 9 = 7\), etc.
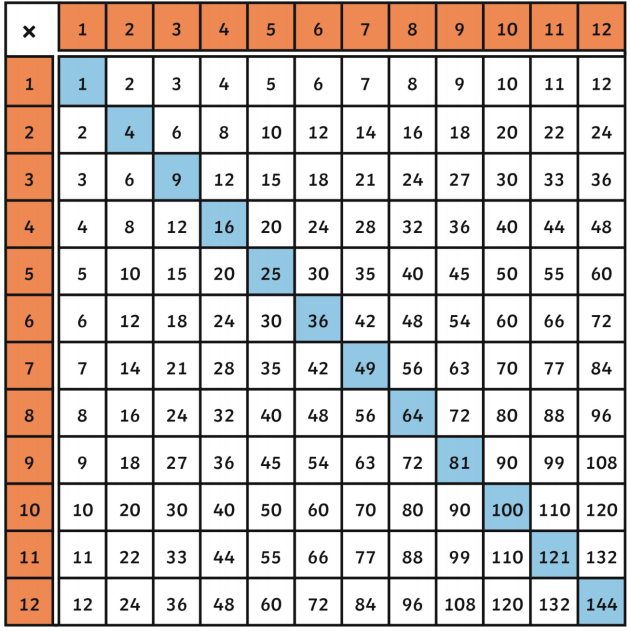
Visual Representation
Square numbers can be visually represented as square arrays of dots. For instance, the number 9 can be represented as a 3x3 grid of dots:
| ● | ● | ● |
| ● | ● | ● |
| ● | ● | ● |
Applications of Square Numbers
Square numbers have numerous applications in various fields of mathematics and science:
- Geometry: They are used in calculating the area of squares.
- Algebra: Square numbers are fundamental in solving quadratic equations.
- Number Theory: They play a significant role in the study of integers and prime numbers.
- Computer Science: Square numbers are used in algorithms and data structure designs.
Finding Square Numbers
To find whether a given number is a square number, you can take the square root of the number and check if it is an integer. For example, to determine if 49 is a square number, compute:
\[
\sqrt{49} = 7
\]
Since 7 is an integer, 49 is a square number.
READ MORE:
Introduction to Square Numbers
Square numbers, also known as perfect squares, are integers that result from multiplying an integer by itself. In mathematical terms, if \( n \) is a square number, then there exists an integer \( k \) such that:
\[
n = k^2
\]
This means that \( n \) is the product of \( k \) multiplied by itself. Square numbers are fundamental in various branches of mathematics and have unique properties that make them significant.
Examples of Square Numbers
- 1 (\(1^2 = 1\))
- 4 (\(2^2 = 4\))
- 9 (\(3^2 = 9\))
- 16 (\(4^2 = 16\))
- 25 (\(5^2 = 25\))
Properties of Square Numbers
- Square numbers are always non-negative since the product of two positive or two negative numbers is positive.
- The square of an even number is even, and the square of an odd number is odd.
- Square numbers can only end in specific digits (0, 1, 4, 5, 6, or 9) in the decimal system.
Visual Representation
Square numbers can be visually represented as square arrays of dots. For instance, the number 9 can be represented as a 3x3 grid of dots:
| ● | ● | ● |
| ● | ● | ● |
| ● | ● | ● |
Significance of Square Numbers
Square numbers are crucial in various areas of mathematics and real-life applications:
- Geometry: They help in calculating areas of squares and understanding geometric shapes.
- Algebra: They are used in solving quadratic equations and other algebraic expressions.
- Number Theory: They play a role in the study of integers and prime numbers.
- Computer Science: Square numbers are important in algorithms and data structures.
Finding Square Numbers
To determine if a given number is a square number, find its square root and check if it is an integer. For example, to verify if 49 is a square number, compute:
\[
\sqrt{49} = 7
\]
Since 7 is an integer, 49 is a square number.
Definition and Basic Concept
Square numbers, also known as perfect squares, are the result of an integer being multiplied by itself. In mathematical notation, a number \( n \) is a square number if there exists an integer \( k \) such that:
\[
n = k^2
\]
This can be understood step by step:
- Identify an Integer: Start with an integer \( k \).
- Multiply by Itself: Multiply this integer by itself to get the square number. For example, if \( k = 3 \), then \( 3 \times 3 = 9 \). Thus, 9 is a square number.
Examples of Square Numbers
Here are some examples of square numbers:
- 1 (\(1^2 = 1\))
- 4 (\(2^2 = 4\))
- 9 (\(3^2 = 9\))
- 16 (\(4^2 = 16\))
- 25 (\(5^2 = 25\))
- 36 (\(6^2 = 36\))
- 49 (\(7^2 = 49\))
- 64 (\(8^2 = 64\))
- 81 (\(9^2 = 81\))
- 100 (\(10^2 = 100\))
Properties of Square Numbers
Square numbers possess unique properties that distinguish them:
- Non-negative: Square numbers are always non-negative since the product of any integer with itself is non-negative.
- Odd and Even Squares: The square of an even number is always even, and the square of an odd number is always odd. For example, \( 4^2 = 16 \) (even) and \( 5^2 = 25 \) (odd).
- Last Digits: In the decimal system, square numbers can only end in specific digits: 0, 1, 4, 5, 6, or 9. This helps in identifying potential square numbers.
Visual Representation
Square numbers can also be represented visually. For example, the number 16 can be depicted as a 4x4 grid of dots:
| ● | ● | ● | ● |
| ● | ● | ● | ● |
| ● | ● | ● | ● |
| ● | ● | ● | ● |
Finding Square Numbers
To determine if a number is a square number, find its square root and check if the result is an integer:
\[
\text{If } n = k^2, \text{ then } k = \sqrt{n}
\]
For instance, to check if 36 is a square number, calculate:
\[
\sqrt{36} = 6
\]
Since 6 is an integer, 36 is a square number.
Visual Representation of Square Numbers
Square numbers, or perfect squares, can be visually represented in various ways, making it easier to understand their properties and significance. Below are some common visual methods to represent square numbers:
Square Grids
One of the most intuitive ways to represent square numbers is through square grids. For instance, the number 9 can be represented as a 3x3 grid of dots:
| ● | ● | ● |
| ● | ● | ● |
| ● | ● | ● |
This grid clearly shows that 9 is a perfect square, as it forms a complete square shape.
Similarly, the number 16 can be represented as a 4x4 grid of dots:
| ● | ● | ● | ● |
| ● | ● | ● | ● |
| ● | ● | ● | ● |
| ● | ● | ● | ● |
This representation makes it easy to see that 16 is a perfect square.
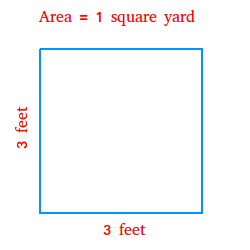
Area Representation
Square numbers can also be represented by the area of squares. For example, a square with a side length of 5 units has an area of:
\[
5 \times 5 = 25 \text{ square units}
\]
This geometric interpretation helps in understanding the spatial aspect of square numbers. Each side of the square represents the integer, and the area represents the square number.
Number Line Representation
Another way to visualize square numbers is on a number line. By plotting the square numbers on a number line, one can easily see the increasing gaps between consecutive square numbers:
\[
1, 4, 9, 16, 25, 36, \ldots
\]
The gaps between consecutive squares increase as the numbers get larger, reflecting the quadratic growth of square numbers.
Summation of Odd Numbers
Square numbers can also be visualized as the sum of consecutive odd numbers. For example, the number 25 can be represented as:
\[
25 = 1 + 3 + 5 + 7 + 9
\]
This summation method provides a clear visual and numerical way to understand how square numbers are built from smaller, consecutive odd numbers.
Patterns in Square Numbers
Observing the patterns in square numbers can be insightful. For instance, the squares of numbers ending in 5 always end in 25:
- \(5^2 = 25\)
- \(15^2 = 225\)
- \(25^2 = 625\)
These patterns help in recognizing and verifying square numbers quickly.
Geometric Applications
Square numbers have numerous geometric applications, many of which stem from their fundamental properties. Here, we explore how square numbers are used in geometry.
Area Calculation
One of the most direct geometric applications of square numbers is in calculating the area of a square. Given a square with side length \(a\), the area \(A\) is given by the formula:
\[ A = a^2 \]
For example, if the side length of a square is 5 units, the area is:
\[ A = 5^2 = 25 \, \text{square units} \]
Diagonal Calculation
The diagonal \(d\) of a square can also be calculated using square numbers. The relationship between the side length \(a\) and the diagonal \(d\) is given by:
\[ d = a\sqrt{2} \]
For instance, if the side length of the square is 4 units, the diagonal length is:
\[ d = 4\sqrt{2} \approx 5.66 \, \text{units} \]
Pythagorean Theorem
Square numbers play a critical role in the Pythagorean theorem, which relates the lengths of the sides of a right-angled triangle. For a right-angled triangle with legs \(a\) and \(b\), and hypotenuse \(c\), the theorem states:
\[ a^2 + b^2 = c^2 \]
This equation shows how square numbers are used to find the length of one side of the triangle when the other two sides are known.
Tiling and Patterns
Square numbers are also essential in creating tiling patterns and designs. For example, a grid pattern composed of square tiles can be arranged to form larger squares. If each small square tile has a side length of 1 unit, then a grid that forms a larger square of side length \(n\) units will contain:
\[ n^2 \, \text{tiles} \]
This concept is frequently used in architecture and interior design to create aesthetically pleasing and mathematically precise layouts.
Geometric Proofs and Constructions
Square numbers are used in various geometric proofs and constructions. For example, proving the area relationships in geometric figures often involves squaring lengths and manipulating these squares algebraically. Additionally, constructions involving perfect squares help in visualizing and solving complex geometric problems.
In summary, square numbers are integral to many geometric concepts and applications. They help in calculating areas, understanding relationships in geometric figures, designing patterns, and constructing precise mathematical proofs.
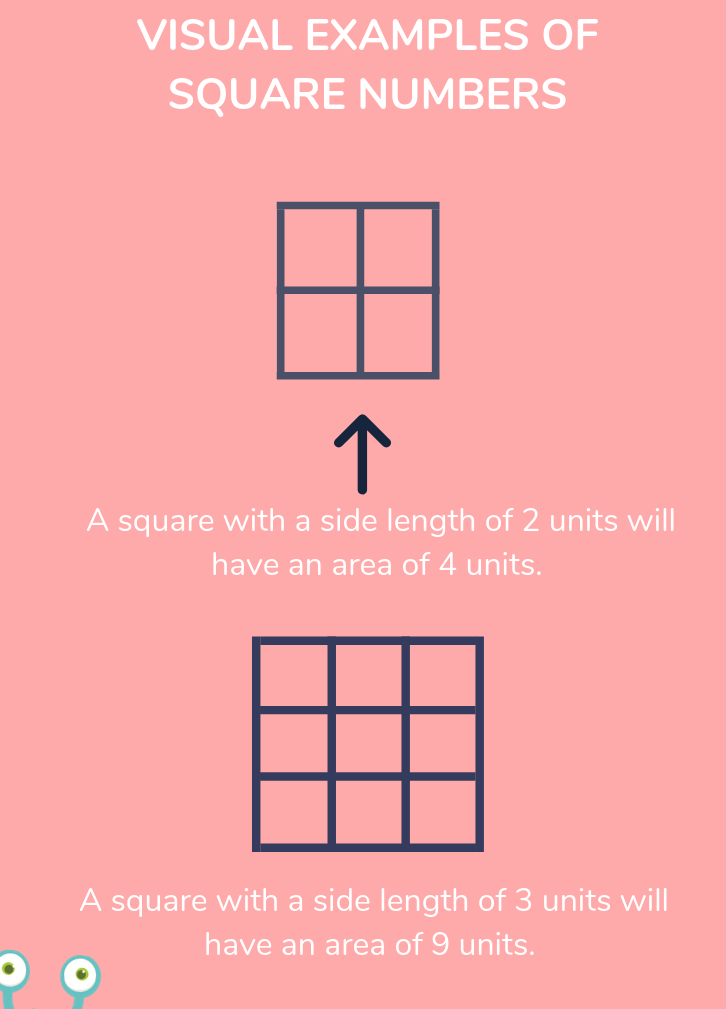
Algebraic Applications
Square numbers have numerous applications in algebra, often used to simplify expressions, solve equations, and understand various mathematical properties. Below are some key algebraic applications of square numbers:
Solving Quadratic Equations
Quadratic equations are polynomial equations of the form:
\[ ax^2 + bx + c = 0 \]
Square numbers are integral in solving these equations using methods such as factoring, completing the square, and the quadratic formula. For example, consider the quadratic equation:
\[ x^2 - 4 = 0 \]
Factoring this, we get:
\[ (x - 2)(x + 2) = 0 \]
Thus, the solutions are:
\[ x = 2 \, \text{and} \, x = -2 \]
Completing the Square
Completing the square is a method used to solve quadratic equations by converting them into perfect square trinomials. For example, for the equation:
\[ x^2 + 6x + 5 = 0 \]
We rewrite it as:
\[ x^2 + 6x + 9 = 4 \]
Which simplifies to:
\[ (x + 3)^2 = 4 \]
Taking the square root of both sides, we get:
\[ x + 3 = \pm 2 \]
Thus, the solutions are:
\[ x = -1 \, \text{and} \, x = -5 \]
Properties of Exponents
Square numbers frequently appear in the properties of exponents. For example, the property:
\[ (a^m)^n = a^{mn} \]
When \( n = 2 \), we have:
\[ (a^m)^2 = a^{2m} \]
Illustrating how squaring an exponent affects the power of a base number.
Binomial Theorem
Square numbers also appear in the binomial theorem, which describes the algebraic expansion of powers of a binomial. For example:
\[ (a + b)^2 = a^2 + 2ab + b^2 \]
This expansion shows how square numbers and their coefficients arise naturally in polynomial expansions.
Inequalities Involving Squares
Square numbers help in solving inequalities, particularly those involving quadratic expressions. For instance, to solve:
\[ x^2 \leq 9 \]
We rewrite this as:
\[ -3 \leq x \leq 3 \]
Demonstrating how square roots are used to determine the solution range.
Graphing Parabolas
The graph of a quadratic function \( y = ax^2 + bx + c \) is a parabola. The vertex form of a quadratic function:
\[ y = a(x - h)^2 + k \]
Utilizes square numbers to determine the vertex and the shape of the parabola.
In summary, square numbers are foundational in algebra, facilitating the solving of equations, simplifying expressions, and understanding the properties of exponents and polynomials.
Number Theory Applications
Square numbers play a significant role in number theory, a branch of pure mathematics focused on the properties and relationships of numbers, particularly integers. Here, we explore some of the primary applications of square numbers in number theory:
- Pythagorean Triples
Pythagorean triples are sets of three positive integers \( (a, b, c) \) that satisfy the equation \( a^2 + b^2 = c^2 \). These triples are fundamental in number theory and have applications in various areas such as geometry and algebra.
Example: \( (3, 4, 5) \) is a Pythagorean triple because \( 3^2 + 4^2 = 9 + 16 = 25 = 5^2 \).
- Fermat's Last Theorem
Square numbers are integral to Fermat's Last Theorem, which states that there are no three positive integers \( a, b, \) and \( c \) that can satisfy the equation \( a^n + b^n = c^n \) for any integer value of \( n \) greater than 2. This theorem remained unproven for centuries until Andrew Wiles provided a proof in 1994.
- Quadratic Forms
In number theory, a quadratic form is a polynomial with terms all of degree two. Square numbers are often used in these forms to represent numbers in different ways, such as representing numbers as sums of two squares or more.
Example: The sum of two squares theorem states that a number can be expressed as the sum of two squares if and only if in its prime factorization, every prime of the form \( 4k+3 \) occurs with an even exponent.
- Modular Arithmetic
Square numbers also appear in modular arithmetic, particularly in problems involving quadratic residues. A quadratic residue modulo \( n \) is an integer \( q \) such that there exists an integer \( x \) satisfying \( x^2 \equiv q \ (\text{mod} \ n) \).
Example: In modulo 7, the quadratic residues are 0, 1, 2, and 4 because the squares of the integers \( 0, 1, 2, 3, 4, 5, \) and \( 6 \) modulo 7 result in these values.
Understanding these applications helps in exploring deeper concepts in number theory and reveals the beauty of mathematical relationships.
Computer Science Applications
Square numbers play a significant role in various computer science applications. Below are detailed explanations of their applications in this field:
-
Algorithm Optimization:
Square numbers are often used in optimizing algorithms, especially in problems involving spatial computations and matrix operations. For example, the time complexity of some algorithms is expressed in terms of square numbers, such as \(O(n^2)\) for certain sorting algorithms.
-
Data Structures:
Square numbers are crucial in data structures like matrices and arrays. In computer graphics and image processing, square matrices are used to perform transformations and operations efficiently.
-
Graph Theory:
In graph theory, square numbers help in defining properties and operations on graphs. The adjacency matrix of a graph, which is a square matrix, is fundamental in representing the connections between nodes.
-
Cryptography:
Square numbers are essential in cryptographic algorithms. For instance, the RSA encryption algorithm relies on the difficulty of factoring large products of prime numbers, which inherently involves calculations with square numbers.
-
Error Detection and Correction:
Square numbers are used in error detection and correction algorithms, such as parity check codes and Hamming codes. These codes help in identifying and correcting errors in data transmission.
-
Machine Learning:
In machine learning, square numbers are involved in calculations of loss functions, which are often quadratic in nature. Minimizing these loss functions helps in training accurate predictive models.
-
Simulation and Modeling:
Square numbers are used in simulations and modeling, particularly in physics-based simulations where spatial dimensions are represented as square grids.
Methods to Identify Square Numbers
Square numbers, also known as perfect squares, are numbers that can be expressed as the product of an integer with itself. Here are some methods to identify square numbers:
-
Direct Multiplication:
To find if a number \( n \) is a square number, you can determine if there exists an integer \( x \) such that \( x \times x = n \). For example, 16 is a square number because \( 4 \times 4 = 16 \).
-
Prime Factorization:
A number is a square number if all the exponents in its prime factorization are even. For example, the prime factorization of 36 is \( 2^2 \times 3^2 \), which confirms 36 is a square number because all exponents are even.
Number Prime Factorization Square Number? 36 \( 2^2 \times 3^2 \) Yes 18 \( 2^1 \times 3^2 \) No -
Check the Last Digits:
Square numbers can only end in 0, 1, 4, 5, 6, or 9 in base 10. If a number ends in any other digit, it is not a square number.
Examples:
- 25 (ends in 5) - Square number
- 32 (ends in 2) - Not a square number
-
Sum of Odd Numbers:
A square number is the sum of the first \( n \) odd numbers. For instance, \( 4^2 = 1 + 3 + 5 + 7 = 16 \).
Example:
- 1 = 1
- 1 + 3 = 4
- 1 + 3 + 5 = 9
- 1 + 3 + 5 + 7 = 16
-
Using a Calculator:
You can use a calculator to find the square root of the number. If the square root is an integer, the original number is a square number. For example, the square root of 49 is 7, which is an integer, hence 49 is a square number.
By using these methods, you can efficiently determine whether a given number is a square number.

Historical Context and Significance
Square numbers have a rich history in mathematics, tracing back to ancient civilizations where they played a crucial role in the development of mathematical thought. The study of square numbers can be seen in various ancient texts and mathematical traditions.
- Babylonian Mathematics: Ancient Babylonian mathematicians were among the first to study and use square numbers. They developed methods to calculate areas and solve quadratic equations, which laid the groundwork for the understanding of square numbers.
- Pythagoras and Greek Mathematics: Pythagoras, a prominent Greek mathematician, made significant contributions to the study of numbers. He explored properties of square numbers and is famously known for the Pythagorean theorem, which relates the squares of the sides of a right-angled triangle.
- Chinese Mathematics: Ancient Chinese mathematicians, such as those during the Han Dynasty, also studied square numbers. They developed methods for calculating areas and solving equations involving squares.
- Indian Mathematics: Indian mathematicians like Brahmagupta made significant advances in the study of algebra and square numbers. They developed formulas for solving quadratic equations and contributed to the understanding of square roots.
- Islamic Golden Age: During the Islamic Golden Age, mathematicians like Al-Khwarizmi expanded on the work of earlier civilizations. They translated and preserved Greek and Indian mathematical texts, furthering the study of square numbers and their applications.
- European Renaissance: The Renaissance period in Europe saw a revival of interest in classical mathematics, including the study of square numbers. Mathematicians like Fibonacci and Cardano built on ancient knowledge and made new discoveries in algebra and number theory.
Square numbers have continued to be a fundamental concept in mathematics, influencing various fields such as geometry, algebra, and number theory. Their historical significance lies not only in their practical applications but also in their role in the development of mathematical thought and theory.
| Period | Key Contributions |
|---|---|
| Babylonian | Early methods for calculating areas and solving quadratic equations |
| Greek | Pythagorean theorem, exploration of number properties |
| Chinese | Techniques for area calculation, solving equations involving squares |
| Indian | Advances in algebra, formulas for quadratic equations, understanding of square roots |
| Islamic Golden Age | Preservation and expansion of Greek and Indian mathematical texts |
| European Renaissance | Revival of classical mathematics, new discoveries in algebra and number theory |
Difference Between Consecutive Square Numbers
The difference between consecutive square numbers reveals interesting patterns and relationships in mathematics. For any integer \( n \), the square of \( n+1 \) and the square of \( n \) are consecutive square numbers. The difference between these squares can be calculated as follows:
Let \( n \) be an integer. Then, the square of \( n \) is \( n^2 \), and the square of \( n+1 \) is \((n+1)^2\). The difference between these consecutive squares is:
\[
(n+1)^2 - n^2
\]
Expanding the squares, we get:
\[
(n^2 + 2n + 1) - n^2 = 2n + 1
\]
This result shows that the difference between consecutive square numbers is always an odd number. Specifically, it is the sum of twice the smaller integer and one. This pattern can be seen in examples:
- For \( n = 1 \): \((1+1)^2 - 1^2 = 4 - 1 = 3\)
- For \( n = 2 \): \((2+1)^2 - 2^2 = 9 - 4 = 5\)
- For \( n = 3 \): \((3+1)^2 - 3^2 = 16 - 9 = 7\)
These differences (3, 5, 7, ...) form a sequence of consecutive odd numbers.
The algebraic proof can be generalized as follows:
For any two integers \( a \) and \( b \), where \( b = a + 1 \), the difference between their squares is:
\[
b^2 - a^2 = (a + 1)^2 - a^2 = a^2 + 2a + 1 - a^2 = 2a + 1
\]
This property highlights a fundamental aspect of the structure of square numbers and is an important concept in number theory.
Additionally, this rule can be extended to differences between squares of numbers that are not consecutive. For example, the difference between squares of \( n+2 \) and \( n \) is:
\[
(n+2)^2 - n^2 = n^2 + 4n + 4 - n^2 = 4n + 4
\]
This can be generalized further. If \( b = a + k \), where \( k \) is any positive integer, the difference between the squares is:
\[
b^2 - a^2 = (a + k)^2 - a^2 = a^2 + 2ak + k^2 - a^2 = 2ak + k^2
\]
Thus, the difference between the squares of two numbers is dependent on both the values of the numbers and the distance \( k \) between them.
Patterns in Square Numbers
Square numbers exhibit interesting and recognizable patterns that can be explored in various mathematical contexts. Here are some key patterns observed in square numbers:
- Basic Sequence Pattern: Square numbers follow a simple sequence where each number is the square of a consecutive natural number. The sequence can be written as: This translates to:
- Difference Between Consecutive Squares: The difference between consecutive square numbers forms an arithmetic sequence. If \( n^2 \) and \((n+1)^2\) are two consecutive squares, their difference is: For example, \(4-1 = 3\), \(9-4 = 5\), \(16-9 = 7\), showing the differences 3, 5, 7, etc.
- Sum of Odd Numbers: Each square number is the sum of the first n odd numbers. For instance:
- 1 = 1
- 4 = 1 + 3
- 9 = 1 + 3 + 5
- 16 = 1 + 3 + 5 + 7
- Geometric Pattern: Square numbers can be represented geometrically as points forming a perfect square on a grid. For example, \(3^2 = 9\) can be visualized as a 3x3 grid of dots.
- Sum of Squares Pattern: The sum of the squares of the first n natural numbers has a known formula: For example, the sum of the squares of the first 3 numbers is \(1^2 + 2^2 + 3^2 = 1 + 4 + 9 = 14\).
Understanding these patterns helps in recognizing and predicting square numbers, and they play a significant role in various branches of mathematics and their applications.
Square Numbers in Real Life
Square numbers, or perfect squares, appear in many real-life contexts. These applications highlight the practicality and ubiquity of this fundamental mathematical concept.
- Floor and Wall Tiles: Square tiles are commonly used in construction for both floors and walls. Their uniform shape makes it easy to calculate the number needed and ensures a neat, organized appearance.
- Chess Board: A chessboard consists of 64 small squares arranged in an 8x8 grid. This setup is essential for the game, demonstrating how square numbers facilitate gameplay and organization.
- Books and Paper Napkins: Many small books, especially those for children, are square-shaped for easy handling. Similarly, paper napkins often unfold into large squares, making them practical for use.
- Food Items: Common food items like slices of bread, cheese slices, and chocolate bars are often square-shaped. This shape is not only convenient for packaging but also for consumption.
- Windows and Photo Frames: Square windows and photo frames are prevalent in home design. They provide a balanced and aesthetically pleasing look.
- Post-it Notes: These ubiquitous office supplies are usually square-shaped, offering ample space for notes and reminders.
- Keyboards: The keys on many keyboards are square, which helps in efficient use of space and easy identification of each key.
- Logos: Many well-known companies use square logos. For example, the logos of Microsoft and the BBC are square, symbolizing strength and stability.
These examples illustrate that square numbers are not just abstract mathematical concepts but are integral to various practical and aesthetic applications in everyday life.

Square Roots and Their Relationship to Square Numbers
A square root of a number is a value that, when multiplied by itself, gives the original number. The operation of finding a square root is the inverse of squaring a number.
For example, the square root of 25 is 5, because \( 5 \times 5 = 25 \). Similarly, the square root of 16 is 4, as \( 4 \times 4 = 16 \).
Mathematically, if n is a square number, then it can be expressed as \( n = a^2 \) for some integer a. The square root of n is then a:
\(\sqrt{n} = a\)
The symbol for the square root is \( \sqrt{ } \), known as the radical sign. For example:
\(\sqrt{25} = 5\)
Every positive number has two square roots: a positive and a negative. These are often represented as:
\(\sqrt{n} = \pm a\)
So for 25, the square roots are \( +5 \) and \( -5 \), because:
\( 5 \times 5 = 25 \) and \( (-5) \times (-5) = 25 \)
However, when we refer to "the square root" in most contexts, we typically mean the principal (positive) square root.
Properties of Square Roots
- Non-Negative Results: The principal square root of any non-negative number is always non-negative.
- Square of a Square Root: Squaring the square root of a number returns the original number: \( (\sqrt{n})^2 = n \).
- Square Root of a Product: The square root of a product is the product of the square roots: \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \).
- Square Root of a Fraction: The square root of a fraction is the square root of the numerator divided by the square root of the denominator: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Visual Representation of Square Roots
Visually, the square root of a number can be thought of in terms of the area of a square. If a square has an area of \( n \) square units, then the side length of the square is the square root of \( n \).
| Number | Square Root | Visual Representation |
|---|---|---|
| 1 | 1 | |
| 4 | 2 | |
| 9 | 3 | |
| 16 | 4 |
Calculating Square Roots
For perfect squares, calculating the square root is straightforward. For example:
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
For numbers that are not perfect squares, finding the square root might involve approximations or using a calculator. For instance, the square root of 10 is approximately 3.162.
Understanding the relationship between square numbers and their roots is fundamental in mathematics, providing a basis for more advanced topics such as algebra, geometry, and number theory.
Perfect Squares vs. Imperfect Squares
In mathematics, the distinction between perfect squares and imperfect squares is fundamental in understanding how numbers relate to their square roots and their properties. Let's explore these concepts in detail.
What are Perfect Squares?
A perfect square is an integer that is the square of another integer. In other words, if n is a perfect square, there exists some integer k such that:
\( n = k^2 \)
Some examples of perfect squares include:
- 1 (because \( 1 = 1^2 \))
- 4 (because \( 4 = 2^2 \))
- 9 (because \( 9 = 3^2 \))
- 16 (because \( 16 = 4^2 \))
- 25 (because \( 25 = 5^2 \))
Perfect squares have several unique properties:
- Always Non-negative: The square of any real number is always non-negative.
- Odd and Even Properties: The square of an odd number is odd, and the square of an even number is even.
- Sum of Odd Integers: Perfect squares can be expressed as the sum of consecutive odd integers starting from 1. For example, \( 9 = 1 + 3 + 5 \).
In the context of geometry, a perfect square corresponds to a square with an area that is an integer value. For instance, a square with a side length of 5 units has an area of \( 25 \) square units, which is a perfect square.
What are Imperfect Squares?
An imperfect square, also known as a non-perfect square, is a number that cannot be expressed as the square of any integer. These numbers have square roots that are not integers and are often irrational.
Examples of imperfect squares include:
- 2 (since \( \sqrt{2} \) is approximately 1.414, which is not an integer)
- 3 (since \( \sqrt{3} \) is approximately 1.732)
- 5 (since \( \sqrt{5} \) is approximately 2.236)
- 7 (since \( \sqrt{7} \) is approximately 2.646)
- 10 (since \( \sqrt{10} \) is approximately 3.162)
Imperfect squares have unique characteristics:
- Non-integer Roots: The square root of an imperfect square is not an integer.
- Often Irrational: The square roots of many imperfect squares are irrational numbers, meaning they cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions.
- Approximation Needed: To work with the square roots of imperfect squares, we often use approximations or decimal representations.
Visualizing Perfect and Imperfect Squares
To visualize the difference between perfect and imperfect squares, consider the areas of squares:
| Number | Square Root | Type | Visual Representation |
|---|---|---|---|
| 1 | 1 | Perfect Square | |
| 4 | 2 | Perfect Square | |
| 2 | 1.414 | Imperfect Square | |
| 3 | 1.732 | Imperfect Square |
Understanding the distinction between perfect and imperfect squares is crucial for exploring deeper mathematical concepts such as irrational numbers, quadratic equations, and geometric representations.
Exercises and Practice Problems
Here are some exercises and practice problems to help you understand and identify square numbers. Work through each problem step by step and check your answers at the end.
Basic Exercises
- List the first 10 square numbers.
- What is the square of 15?
- Find the square root of 144.
- Is 81 a square number? If yes, what is its square root?
- Which number is larger, the square of 12 or the square of 9?
Intermediate Exercises
- Calculate the squares of the following numbers: 7, 14, 21, 28.
- Find the next square number after 49.
- What two consecutive integers does the square root of 50 lie between?
- Is 225 a perfect square? If yes, what is its square root?
- Determine if 200 is a square number. Explain your reasoning.
Advanced Exercises
- Prove that the sum of the first \(n\) odd numbers is equal to \(n^2\). For example, the sum of the first 5 odd numbers (1, 3, 5, 7, 9) is 25, which is \(5^2\).
- Show that the difference between the squares of two consecutive integers \(n\) and \(n+1\) is always an odd number.
- Find three consecutive square numbers and verify that their differences form an arithmetic sequence.
- Solve the equation \(x^2 - 6x + 9 = 0\) and explain the significance of the roots in relation to square numbers.
- If the area of a square is 169 square units, find the length of one side of the square.
Real-World Problems
- A square garden has an area of 625 square feet. What is the length of one side of the garden?
- Find the side length of a square that has the same area as a rectangle with sides 6 cm and 8 cm.
- A car travels 225 miles. Assuming the distance traveled forms a perfect square, what could be the possible side lengths of the square in miles?
- The diagonal of a square is 10√2 meters. Find the side length of the square.
- A square field has a perimeter of 48 meters. What is the area of the field?
Practice Problems with Answers
| Problem | Answer |
|---|---|
| Square of 15 | 225 |
| Square root of 144 | 12 |
| Is 81 a square number? | Yes, its square root is 9 |
| First 10 square numbers | 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 |
| Next square number after 49 | 64 |
Common Misconceptions About Square Numbers
Square numbers, or perfect squares, often lead to various misconceptions among students and even adults. Here, we will address some of the common misunderstandings to clarify these concepts.
- Misconception 1: Any number squared is a square number
Not every number when squared results in a square number. A square number must be an integer. For example, \( (1.5)^2 = 2.25 \) is not a square number because 2.25 is not an integer.
- Misconception 2: All square numbers are even
Square numbers can be both even and odd. For instance, \( 4 = 2^2 \) is an even square number, while \( 9 = 3^2 \) is an odd square number.
- Misconception 3: Square numbers end in any digit
Square numbers end in specific digits. They end in 0, 1, 4, 5, 6, or 9. For example, the square of 3 is 9, and the square of 5 is 25.
- Misconception 4: The square root of a number always results in a whole number
Only perfect squares have whole number square roots. For example, \( \sqrt{16} = 4 \), but \( \sqrt{20} \) is not a whole number.
- Misconception 5: Multiplying any two equal numbers results in a square number
Only when both numbers are the same integer does their product result in a square number. For example, \( 5 \times 5 = 25 \) is a square number, but \( 5 \times 6 = 30 \) is not.
- Misconception 6: Square numbers are always positive
While the squares of positive and negative integers are positive, the concept of square numbers primarily applies to non-negative integers. Negative results come from squaring complex numbers, which is beyond basic square numbers.
- Misconception 7: The product of two square numbers is always a square number
This is actually true. The product of two square numbers is a square number. For instance, \( 4 \times 9 = 36 \) and \( \sqrt{36} = 6 \).
Understanding these misconceptions helps in grasping the correct properties and applications of square numbers in mathematics.

Conclusion
Square numbers are fundamental elements in mathematics, arising from multiplying a number by itself. They play a crucial role in various areas of mathematics, from basic arithmetic to more advanced topics like algebra and number theory.
Some key points about square numbers include:
- Definition: A square number is the product of an integer multiplied by itself, denoted as \( n^2 \). For example, \( 4^2 = 16 \).
- Properties: Square numbers are always positive, and the square of an even number is even, while the square of an odd number is odd.
- Visual Representation: Square numbers can be represented visually as perfect squares in a grid, reinforcing their geometric significance.
- Applications: They appear in various real-world applications, including geometry, algebra, computer science, and number theory. For instance, they help in calculating areas and solving quadratic equations.
- Patterns: Square numbers follow specific patterns, such as the difference between consecutive squares being odd numbers.
Understanding square numbers not only helps in solving mathematical problems but also enhances logical reasoning and problem-solving skills. They serve as building blocks for more complex concepts and their study lays the foundation for higher mathematics. Exploring square numbers reveals fascinating patterns and relationships, making mathematics both intriguing and rewarding.
In summary, square numbers are simple yet profound, offering insights and applications that extend far beyond their initial definition. Their study is essential for anyone looking to deepen their understanding of mathematics and its numerous applications.
Số Vuông Giải Thích
READ MORE:
Số Vuông Là Gì | Các Con Số | Toán Học | FuseSchool