Topic what are square numbers in math: Square numbers, also known as perfect squares, are essential in mathematics, offering both simplicity and depth. This guide explores their definition, properties, and applications, making the concept easy to grasp for learners and intriguing for enthusiasts. Discover how square numbers play a crucial role in various mathematical contexts and everyday scenarios.
Table of Content
- Square Numbers in Mathematics
- Introduction to Square Numbers
- Definition of Square Numbers
- Visual Representation of Square Numbers
- Patterns in Square Numbers
- Applications of Square Numbers
- Historical Background of Square Numbers
- Square Numbers in Geometry
- Square Numbers and Algebra
- Relationship with Other Numbers
- Square Numbers in Modern Mathematics
- Challenges Involving Square Numbers
- Conclusion
- YOUTUBE: Tìm hiểu về các số hình vuông trong toán học với video này. Hãy cùng khám phá các khái niệm và ví dụ minh họa chi tiết.
Square Numbers in Mathematics
Square numbers, also known as perfect squares, are integers that can be expressed as the square of another integer. In other words, a number \( n \) is a square number if there exists an integer \( k \) such that:
\( n = k^2 \)
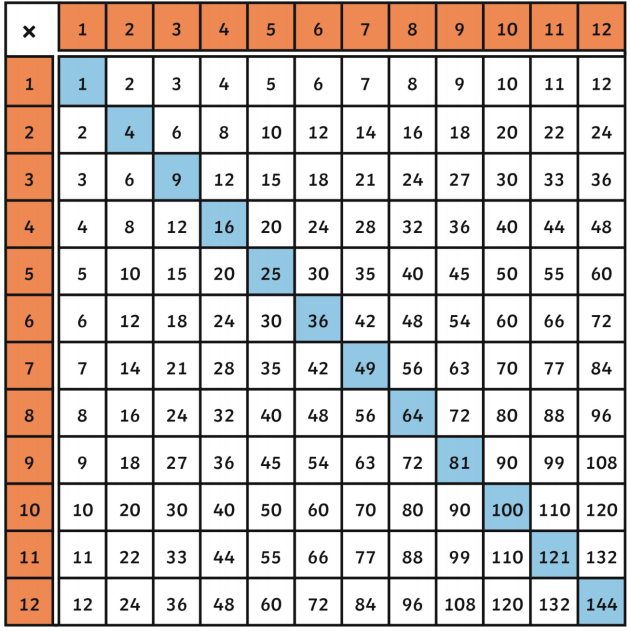
Examples of Square Numbers
- 1 = \( 1^2 \)
- 4 = \( 2^2 \)
- 9 = \( 3^2 \)
- 16 = \( 4^2 \)
- 25 = \( 5^2 \)
- 36 = \( 6^2 \)
- 49 = \( 7^2 \)
- 64 = \( 8^2 \)
- 81 = \( 9^2 \)
- 100 = \( 10^2 \)
Properties of Square Numbers
- They are always non-negative.
- They grow quadratically as the integer increases.
- The difference between consecutive square numbers increases linearly. For example, the difference between \( 4 \) and \( 9 \) is \( 5 \), and the difference between \( 9 \) and \( 16 \) is \( 7 \).
- Every square number has an odd number of total divisors.
- In a sequence of natural numbers, squares of even numbers are even, and squares of odd numbers are odd.
Square Numbers and Geometry
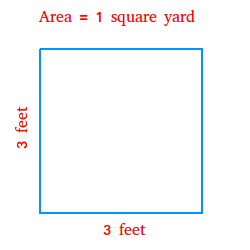
Square numbers can be visually represented in geometry. For example, a square of side length \( k \) has an area equal to \( k^2 \), which is a square number.
Square Numbers in Number Theory
In number theory, square numbers have significance in various theorems and properties, such as:
- Fermat's theorem on sums of two squares.
- Lagrange's four-square theorem.
- Pythagorean triples involving squares.
Table of Square Numbers
| Integer | Square Number |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
Understanding square numbers is fundamental in both basic arithmetic and more advanced areas of mathematics, including algebra and number theory.
READ MORE:
Introduction to Square Numbers
Square numbers, or perfect squares, are a fundamental concept in mathematics. These numbers are the result of multiplying an integer by itself. Mathematically, a number \( n \) is considered a square number if it can be expressed as:
\( n = k^2 \)
where \( k \) is an integer. This means the integer \( k \) multiplied by itself equals the square number \( n \).
Examples of Square Numbers
Here are some basic examples to illustrate square numbers:
- 1 = \( 1^2 \)
- 4 = \( 2^2 \)
- 9 = \( 3^2 \)
- 16 = \( 4^2 \)
- 25 = \( 5^2 \)
- 36 = \( 6^2 \)
- 49 = \( 7^2 \)
- 64 = \( 8^2 \)
- 81 = \( 9^2 \)
- 100 = \( 10^2 \)
Visualizing Square Numbers
Square numbers can be visualized as squares on a grid, where the side length of each square corresponds to the integer \( k \). For instance:
| Side Length | Square Number |
| 1 | 1 (1x1) |
| 2 | 4 (2x2) |
| 3 | 9 (3x3) |
| 4 | 16 (4x4) |
| 5 | 25 (5x5) |
Properties of Square Numbers
Square numbers possess several key properties:
- They are always non-negative.
- The difference between consecutive square numbers increases by an odd integer (e.g., \( 4 - 1 = 3 \), \( 9 - 4 = 5 \)).
- Their square roots are always integers.
- Squares of even numbers are even, and squares of odd numbers are odd.
Understanding square numbers is crucial for exploring various mathematical concepts, from basic arithmetic to advanced algebra and geometry.
Definition of Square Numbers
In mathematics, square numbers are a special category of integers that are the result of multiplying a number by itself. Formally, a square number is defined as:
\( n = k^2 \)
where \( n \) is the square number and \( k \) is the integer whose square gives \( n \).
Characteristics of Square Numbers
Square numbers have distinctive characteristics:
- They are always non-negative, as the product of an integer with itself cannot be negative.
- They form a quadratic sequence, increasing rapidly as the integer \( k \) increases.
- The square of any integer \( k \) is represented as \( k \times k \).
Basic Examples
Here are some simple examples of square numbers:
- 1 = \( 1^2 \)
- 4 = \( 2^2 \)
- 9 = \( 3^2 \)
- 16 = \( 4^2 \)
- 25 = \( 5^2 \)
Visual Representation
Square numbers can also be visualized as square grids. For example:
| Integer (\( k \)) | Square Number (\( k^2 \)) | Grid Representation |
| 1 | 1 | ■ |
| 2 | 4 | ■■ ■■ |
| 3 | 9 | ■■■ ■■■ ■■■ |
| 4 | 16 | ■■■■ ■■■■ ■■■■ ■■■■ |
| 5 | 25 | ■■■■■ ■■■■■ ■■■■■ ■■■■■ ■■■■■ |
Mathematical Formula
The general formula for a square number is straightforward:
\( n = k^2 \)
where \( n \) is the square number and \( k \) is any integer.
Understanding Square Roots
The inverse of a square number is its square root. For a square number \( n \), the square root is:
\( \sqrt{n} = k \)
Square roots provide the value of \( k \) for which \( k^2 = n \).
Square numbers form the basis of various mathematical concepts and are instrumental in understanding higher-level topics in algebra and geometry.
Visual Representation of Square Numbers
Square numbers can be easily understood and appreciated through their visual representation. These numbers form perfect squares on a grid, providing an intuitive way to grasp their nature. Let's explore various visual aspects of square numbers:
Basic Grid Visualization
A square number can be visualized as a grid where the total number of units forms a perfect square. For example:
- 1: A 1x1 grid, representing \( 1^2 = 1 \).
- 4: A 2x2 grid, representing \( 2^2 = 4 \).
- 9: A 3x3 grid, representing \( 3^2 = 9 \).
Table of Square Numbers
Here is a table showing integers and their corresponding square numbers visualized on a grid:
| Integer (\( k \)) | Square Number (\( k^2 \)) | Grid Representation |
| 1 | 1 | ■ |
| 2 | 4 | ■■ ■■ |
| 3 | 9 | ■■■ ■■■ ■■■ |
| 4 | 16 | ■■■■ ■■■■ ■■■■ ■■■■ |
| 5 | 25 | ■■■■■ ■■■■■ ■■■■■ ■■■■■ ■■■■■ |
Geometric Representation
Square numbers can also be represented geometrically as squares on a plane, where the side length of each square corresponds to the integer \( k \). For instance:
- For \( k = 2 \): A square with a side length of 2 units represents the area \( 2^2 = 4 \) square units.
- For \( k = 3 \): A square with a side length of 3 units represents the area \( 3^2 = 9 \) square units.
- For \( k = 4 \): A square with a side length of 4 units represents the area \( 4^2 = 16 \) square units.
Pattern Recognition
Visualizing square numbers helps in recognizing patterns, such as the incremental growth of square numbers. For instance, adding consecutive odd numbers gives the next square:
\( 1 + 3 = 4 \)
\( 4 + 5 = 9 \)
\( 9 + 7 = 16 \)
Connecting with Algebra
In algebra, square numbers correspond to the terms in binomial expansions and quadratic equations. Their geometric representation aligns with the formula:
\( a^2 + 2ab + b^2 \)
Through these visual and geometric representations, square numbers become more tangible, aiding in the comprehension of their properties and applications in mathematics.
Patterns in Square Numbers
Square numbers exhibit fascinating and predictable patterns that can be explored through various mathematical lenses. These patterns not only reveal intrinsic properties but also provide insights into broader mathematical concepts. Let's delve into some of the key patterns found in square numbers:
1. Differences Between Consecutive Squares
The difference between consecutive square numbers is always an odd number. Specifically, for integers \( k \) and \( k+1 \), the difference between their squares is:
\( (k+1)^2 - k^2 = 2k + 1 \)
For example:
- \( 4 - 1 = 3 \)
- \( 9 - 4 = 5 \)
- \( 16 - 9 = 7 \)
- \( 25 - 16 = 9 \)
2. Sum of Odd Numbers
Each square number can be expressed as the sum of consecutive odd numbers. For integer \( k \), the square \( k^2 \) is the sum of the first \( k \) odd numbers:
\( k^2 = \sum_{i=1}^{k} (2i - 1) \)
For example:
- \( 1 = 1 \)
- \( 4 = 1 + 3 \)
- \( 9 = 1 + 3 + 5 \)
- \( 16 = 1 + 3 + 5 + 7 \)
3. Middle Term Pattern
The middle term in the sequence of consecutive square numbers can be identified through a simple pattern. If \( n \) is odd, the middle term of the sum of the first \( n \) odd numbers will be:
\( \frac{n^2 + 1}{2} \)
4. Parity of Square Numbers
The parity (odd or even nature) of a square number is the same as that of the integer it squares:
- The square of an even number is even.
- The square of an odd number is odd.
For instance:
- \( 2^2 = 4 \) (even)
- \( 3^2 = 9 \) (odd)
- \( 4^2 = 16 \) (even)
- \( 5^2 = 25 \) (odd)
5. Digit Patterns in Square Numbers
Square numbers often display interesting patterns in their digits:
- Any square number will end in 0, 1, 4, 5, 6, or 9 in base 10.
- No square number ends in 2, 3, 7, or 8.
For example:
- \( 16 \), \( 25 \), \( 49 \), \( 81 \), \( 100 \)
6. Pythagorean Triplets
Square numbers are integral to the formation of Pythagorean triplets, where the sum of the squares of two integers equals the square of a third integer:
\( a^2 + b^2 = c^2 \)
For instance:
- \( 3^2 + 4^2 = 5^2 \)
- \( 5^2 + 12^2 = 13^2 \)
- \( 8^2 + 15^2 = 17^2 \)
7. Algebraic and Geometric Patterns
Square numbers frequently appear in algebraic identities and geometric arrangements:
- Squares form perfect squares in geometric grids.
- In algebra, identities such as \( (a + b)^2 = a^2 + 2ab + b^2 \) utilize square numbers.
8. Growth Rate of Square Numbers
The growth rate of square numbers follows a quadratic progression, which can be seen in the rapid increase of their values:
\( n^2 \) grows faster than \( n \) linearly.
Understanding these patterns helps in recognizing and predicting the behavior of square numbers, providing a deeper comprehension of their role in mathematical structures and problem-solving.

Applications of Square Numbers
Square numbers, also known as perfect squares, have numerous applications across various fields. Below are some of the key applications of square numbers in different domains:
1. Geometry
In geometry, square numbers are fundamental in calculating the area of squares. If a square has a side length of \(a\), the area \(A\) is given by:
\[
A = a^2
\]
For example, a square with a side length of 4 units has an area of \(4^2 = 16\) square units.
2. Algebra
Square numbers play a crucial role in algebra, especially in solving quadratic equations. The standard form of a quadratic equation is:
\[
ax^2 + bx + c = 0
\]
Here, the term \(x^2\) represents a squared variable, which is essential in finding the roots of the equation.
3. Number Theory
In number theory, square numbers are used to explore properties and relationships between integers. They help in understanding concepts like prime numbers, divisibility, and the Pythagorean theorem.
4. Computer Science
Square numbers are used in various algorithms and data structures. For instance, they are applied in hash functions and cryptographic algorithms to ensure data security and efficient searching.
5. Physics
In physics, square numbers are used to calculate quantities like kinetic energy (\(E_k\)) and potential energy (\(E_p\)). For kinetic energy, the formula is:
\[
E_k = \frac{1}{2}mv^2
\]
where \(m\) is the mass and \(v\) is the velocity of an object.
6. Engineering
Engineers use square numbers in structural analysis to determine the stress and strength of materials. For example, the bending stress \(\sigma\) in a beam is proportional to the square of its length:
\[
\sigma = \frac{My}{I}
\]
where \(M\) is the moment, \(y\) is the distance from the neutral axis, and \(I\) is the moment of inertia, which involves squared terms of dimensions.
7. Financial Mathematics
In financial mathematics, square numbers are used in compound interest calculations and in modeling various financial instruments. The compound interest formula includes squared terms when calculating interest over multiple periods.
8. Everyday Applications
Square numbers appear in everyday life, such as in calculating areas of rooms, tiles, and other square-shaped objects. They are also used in sports to design fields and courts with precise dimensions.
Overall, the concept of square numbers is integral to both theoretical and practical aspects of mathematics and its applications in various fields.
Historical Background of Square Numbers
Square numbers, or perfect squares, have a rich history in mathematics, dating back to ancient civilizations. The concept of squaring numbers was known to the Babylonians as early as 1800 BCE. They used geometric methods to calculate the squares of numbers, which were crucial for their astronomical and architectural calculations.
In ancient Greece, the study of square numbers was significantly advanced by the Pythagoreans, a group led by the philosopher and mathematician Pythagoras. They discovered important relationships between numbers, including the famous Pythagorean Theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides:
\( a^2 + b^2 = c^2 \)
This theorem not only involves square numbers but also laid the groundwork for much of modern geometry.
Later, the Greek mathematician Euclid, in his seminal work "Elements," provided geometric proofs of the properties of square numbers, contributing significantly to number theory. Euclid's work demonstrated that the difference between successive square numbers is always an odd number:
\( (n+1)^2 - n^2 = 2n + 1 \)
During the Islamic Golden Age, mathematicians like Al-Khwarizmi expanded on Greek knowledge and introduced algebraic methods for solving quadratic equations, which are fundamentally related to the properties of square numbers.
In the Renaissance, mathematical exploration of square numbers continued with the work of European mathematicians such as Fermat, who studied properties of numbers and their sums of squares. Fermat's Last Theorem, although primarily concerned with higher powers, also touches on the unique properties of square numbers.
In modern mathematics, square numbers are fundamental in various fields such as algebra, geometry, and number theory. They are also pivotal in solving quadratic equations, analyzing sequences, and understanding the properties of integers.
Square Numbers in Geometry
Square numbers, also known as perfect squares, are integral to various geometric concepts and applications. In geometry, a square is a four-sided polygon, known as a quadrilateral, with equal sides and equal angles of 90 degrees each. This unique shape and its properties are foundational in understanding square numbers in geometric contexts.
Properties of a Square
- All four sides are equal in length.
- All four angles are equal to 90 degrees.
- The diagonals of a square are equal in length and bisect each other at 90 degrees.
Area and Perimeter
The area of a square can be calculated by squaring the length of one of its sides. If a is the length of a side, the area (A) is given by:
\( A = a^2 \)
The perimeter (P) of a square, which is the total length around the shape, is given by:
\( P = 4a \)
Diagonals of a Square
The diagonals of a square are particularly interesting as they not only bisect each other at right angles but also divide the square into two congruent right-angled triangles. The length of a diagonal (d) can be calculated using the Pythagorean theorem:
\( d = a\sqrt{2} \)
Visual Representation and Construction
Constructing a square is a basic exercise in geometry. Here is a step-by-step method to draw a square using a compass and a straightedge:
- Draw a line segment PQ of the desired length.
- Using P and Q as centers, draw arcs of the same radius that intersect at points above and below the line segment.
- Connect these intersection points to form a perpendicular bisector of PQ.
- Repeat the process to create all four sides of the square.
This geometric construction ensures that all sides are equal and all angles are right angles.
Applications of Square Numbers in Geometry
- Designing and analyzing floor plans, where rooms are often modeled as squares or rectangles.
- Understanding tiling patterns, especially in mosaic and floor designs, where square tiles are commonly used.
- Analyzing and solving problems related to the area and perimeter in various real-world contexts, such as agriculture (plotting land) and architecture (designing buildings).
Square numbers provide a fundamental basis for various geometric principles and applications, making them essential in both theoretical and practical aspects of mathematics.
Square Numbers and Algebra
Square numbers play a crucial role in algebra, where they are often represented using exponents. In algebraic terms, squaring a number is denoted by raising it to the power of two, as in \(x^2\).
Here are some key points about square numbers in algebra:
Basic Definition: A square number is the product of a number multiplied by itself. For example, \(3^2 = 3 \times 3 = 9\).
Variables and Squaring: Just as numbers can be squared, so can variables. For instance, \(x^2\) represents \(x \times x\). This is a fundamental concept in algebra.
Quadratic Equations: Quadratic equations, which are equations of the form \(ax^2 + bx + c = 0\), prominently feature squared terms. Solving these equations often involves finding the values of \(x\) that satisfy the equation.
To further illustrate the importance of square numbers in algebra, let's explore some applications:
Solving Quadratic Equations: Quadratic equations can be solved using methods such as factoring, completing the square, or the quadratic formula. For example, the quadratic formula \(x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a}\) involves the square root of a squared term \(b^2\).
Pythagorean Theorem: In geometry, the Pythagorean theorem \(a^2 + b^2 = c^2\) relates the squares of the lengths of the sides of a right triangle. This theorem is essential in algebra for solving problems involving right triangles.
Area Calculations: The formula for the area of a square, \(A = s^2\), where \(s\) is the length of a side, uses the concept of squaring. Similarly, the area of a circle, \(A = \pi r^2\), involves squaring the radius.
Square numbers are also fundamental in various algebraic manipulations and transformations:
Factoring Expressions: Algebraic expressions can often be simplified by recognizing and factoring out squares. For instance, the difference of squares formula \(a^2 - b^2 = (a - b)(a + b)\) is a powerful tool in algebra.
Expanding Binomials: The square of a binomial expression \((a + b)^2\) expands to \(a^2 + 2ab + b^2\), showcasing how squaring terms can be used in polynomial expansions.
Overall, square numbers are integral to algebraic theory and practice, providing the foundation for solving equations, calculating areas, and performing various algebraic operations.

Relationship with Other Numbers
Square numbers have intriguing relationships with various other types of numbers in mathematics. These relationships highlight the interconnectedness of different numerical properties and patterns.
Relationship with Odd and Even Numbers
- Squares of even numbers are always even. For example, \(4^2 = 16\) and \(6^2 = 36\).
- Squares of odd numbers are always odd. For instance, \(3^2 = 9\) and \(5^2 = 25\).
Relationship with Triangular Numbers
Square numbers can be represented as the sum of consecutive triangular numbers. The n-th square number \(S_n\) can be expressed as:
\(S_n = T_n + T_{n-1}\)
where \(T_n\) is the n-th triangular number given by:
\(T_n = \frac{n(n+1)}{2}\)
For example, the 6th square number and the 6th triangular number are:
\(S_6 = 6^2 = 36\)
\(T_6 = \frac{6 \cdot 7}{2} = 21\)
So, \(36 = 21 + 15\) (where 15 is the 5th triangular number).
Sum of Consecutive Odd Numbers
Every square number can be expressed as the sum of consecutive odd numbers. The n-th square number is the sum of the first n odd numbers:
\(n^2 = \sum_{k=1}^{n} (2k-1)\)
For example:
\(5^2 = 25 = 1 + 3 + 5 + 7 + 9\)
Centered Square Numbers
A centered square number is a figurate number that represents a square with a dot in the center and all other dots surrounding the center in successive layers. The formula for the n-th centered square number is:
\(C_n = n^2 + (n-1)^2\)
For example:
The 3rd centered square number is \(C_3 = 3^2 + 2^2 = 9 + 4 = 13\).
Difference of Squares
The difference of the squares of two consecutive integers is always an odd number. This can be expressed as:
\(n^2 - (n-1)^2 = 2n - 1\)
For instance:
\(5^2 - 4^2 = 25 - 16 = 9\)
Lagrange's Four Square Theorem
According to Lagrange's Four Square Theorem, every natural number can be represented as the sum of four integer squares:
\(n = w^2 + x^2 + y^2 + z^2\)
For example:
\(12 = 0^2 + 2^2 + 2^2 + 2^2\)
\(20 = 4^2 + 2^2 + 0^2 + 0^2\)
Prime Factorization
A square number’s prime factorization contains only even powers of primes. For instance, the prime factorization of 36 is \(2^2 \cdot 3^2\).
These relationships illustrate the rich structure and interesting properties of square numbers, making them a fundamental concept in number theory and other branches of mathematics.
Square Numbers in Modern Mathematics
Square numbers play a significant role in various fields of modern mathematics. They are utilized in different mathematical theories, computational algorithms, and practical applications.
1. Cryptography
Square numbers are fundamental in cryptography, particularly in algorithms such as the RSA encryption, which relies on the difficulty of factoring large composite numbers. The security of these systems often depends on properties of prime numbers and their squares.
2. Numerical Analysis
In numerical analysis, square numbers help in the development of algorithms for solving differential equations. Methods like the finite difference method use grids that are often arranged in square patterns, leveraging the properties of square numbers for computational efficiency.
3. Geometry and Tessellations
Square numbers are central to geometric concepts and tessellations. For example, in creating fractals and tiling patterns, square numbers ensure uniformity and symmetry. This is especially useful in computer graphics and design.
4. Optimization Problems
Optimization problems in operations research frequently use square matrices. For instance, algorithms for network flows, scheduling, and logistics often involve calculations with square matrices, where the dimensions of the matrix are square numbers.
5. Quantum Computing
In quantum computing, square numbers appear in the study of quantum gates and qubit states. The operations in quantum algorithms sometimes involve matrices of square dimensions to maintain coherence and superposition states.
6. Statistical Analysis
In statistics, square numbers are used in the computation of variance and standard deviation, which are essential measures of data dispersion. These calculations involve squaring differences from the mean.
7. Graph Theory
Graph theory applications include adjacency matrices, which are often square matrices. These matrices help in representing and solving problems related to networks, such as finding the shortest path or maximum flow.
Overall, square numbers are integral to both theoretical and applied mathematics, providing a foundation for various modern mathematical techniques and technologies.
Challenges Involving Square Numbers
Square numbers, though fundamental in mathematics, present a variety of challenges in different contexts. These challenges can arise in number theory, algebra, and practical applications.
-
Finding Square Roots:
One common challenge is finding the square roots of large numbers without a calculator. For example, finding the square root of 2025 requires recognizing that it is \(45^2\). This involves understanding the properties of squares and having a good grasp of number factorization.
-
Sum of Square Numbers:
Problems can involve expressing a number as the sum of square numbers. For instance, solving for two square numbers that add up to a given number, such as finding \(a^2 + b^2 = 61\), requires identifying pairs like \(25 (5^2) + 36 (6^2)\).
-
Negative and Imaginary Numbers:
Square numbers also pose challenges when dealing with negative numbers and imaginary numbers. For example, the square root of a negative number involves imaginary numbers, such as \(\sqrt{-4} = 2i\), introducing complexity in algebraic operations.
-
Proof and Contradiction:
Proof-based problems, such as proving or disproving statements about square numbers, can be particularly challenging. For example, disproving the claim that the sum of three consecutive square numbers is always odd requires finding a counterexample, like \(1 + 4 + 9 = 14\).
-
Area and Geometry:
In geometry, calculating areas and understanding properties of figures based on square numbers can be difficult. For instance, determining the side length of a square with an area of 81 cm2 requires finding \(\sqrt{81} = 9\), but ensuring understanding of units and geometric principles.
-
Complex Algebraic Operations:
Algebraic operations involving squares and square roots, such as solving quadratic equations, require careful manipulation of terms. Problems like \((\sqrt{x})^2 = x\) emphasize the need for precision in handling exponents and radicals.
Addressing these challenges involves a deep understanding of the properties of square numbers, practice with different types of problems, and often, creative problem-solving strategies.
Conclusion
Square numbers are fundamental in mathematics, with wide-ranging applications from geometry to algebra, and number theory to modern mathematics. They form the basis for many mathematical concepts and are used in solving a variety of problems.
Throughout history, square numbers have been studied by mathematicians and have contributed to the development of various mathematical theories. In geometry, they help in understanding shapes, areas, and volumes. In algebra, they are essential for solving quadratic equations and understanding polynomial functions. In number theory, they play a crucial role in the study of integers and their properties.
In modern mathematics, square numbers are integral to various fields, including cryptography, computer science, and advanced theoretical studies. They are used in algorithms for security, data compression, and error detection and correction.
Despite their simplicity, square numbers pose interesting challenges and offer deep insights into the structure of numbers. They continue to be a rich area of exploration for both theoretical and applied mathematics.
In conclusion, the study of square numbers enriches our understanding of mathematics and its applications, highlighting their importance in both historical and modern contexts.

Tìm hiểu về các số hình vuông trong toán học với video này. Hãy cùng khám phá các khái niệm và ví dụ minh họa chi tiết.
Các Số Hình Vuông Giải Thích
READ MORE:
Khám phá số hình vuông là gì trong toán học với video từ FuseSchool. Tìm hiểu các khái niệm và ví dụ chi tiết về số hình vuông.
Số Hình Vuông Là Gì | Các Con Số | Toán Học | FuseSchool