Topic 8 squares: The concept of "8 squares" encompasses a variety of intriguing topics, from quilt patterns and knitting squares to mathematical challenges and educational worksheets. In this article, we delve into the diverse applications and creative ideas involving 8 squares, highlighting their importance in both crafting and learning. Join us as we explore the beauty and complexity of 8 squares in various fields.
Table of Content
- Overview of "8 Squares"
- Introduction
- Geometry and Properties of Squares
- Square Roots and Their Calculation
- Mathematical Patterns and Properties
- Applications in Algebra
- Difference of Squares
- Practical Applications in Quilting
- Educational Resources for Class 8
- Advanced Mathematical Concepts Involving Squares
- YOUTUBE: Xem video để tìm hiểu cách tính số lượng hình vuông trên một bàn cờ 8×8 và tham gia vào cuộc thi toán học thú vị!
Overview of "8 Squares"
The term "8 squares" is associated with various contexts including math puzzles, quilting patterns, and educational resources.
Mathematical Puzzles
Math-related activities involving "8 squares" can be found on various educational platforms:
- : An interactive puzzle where players fill an 8x8 grid with shapes, completing rows or columns of eight to make space for more shapes.
- : A puzzle from NRICH requiring identification of eight hidden squares within a grid of points.
- : Another NRICH challenge that explores how many squares can fit within different rectangular dimensions.
Quilting Patterns
In the world of quilting, "8 squares" often refer to 8-inch square quilt blocks. These are popular for their versatility in creating various quilt projects.
- : Offers free patterns for 8-inch quilt blocks, ideal for projects ranging from baby quilts to full-sized bed quilts. The blocks are small enough for intricate designs and suitable for block exchanges among quilters.
Educational Resources
Educational websites like NRICH provide resources and challenges aimed at different age groups to enhance mathematical problem-solving skills through engaging tasks involving squares and other geometric shapes.

READ MORE:
Introduction
The concept of "8 squares" can be explored in various mathematical and geometrical contexts. Squares are fundamental shapes with unique properties, and their study can involve calculating areas, perimeters, and understanding their applications in different mathematical problems. Whether in algebra, geometry, or practical applications, squares offer numerous insights and interesting challenges.
- Definition and Basic Properties of Squares
- Area and Perimeter Calculations
- Perfect Squares and Square Roots
- Geometric Constructions and Applications
- Squares in Algebra and Arithmetic
- Advanced Properties and Theorems
Geometry and Properties of Squares
A square is a unique quadrilateral with several defining properties and geometric characteristics. Below, we delve into its key aspects:
- Equal Sides: All four sides of a square are of equal length.
- Right Angles: Each of the four interior angles is a right angle, measuring 90 degrees.
- Diagonals:
- Diagonals are equal in length and intersect at right angles.
- They bisect each other, meaning they cut each other into two equal halves.
- The length of each diagonal can be calculated using the formula \(d = s\sqrt{2}\), where \(s\) is the side length of the square.
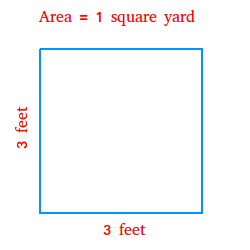
- Perimeter: The perimeter of a square is given by \(P = 4s\), where \(s\) is the side length.
- Area: The area of a square is calculated as \(A = s^2\).
- Circumcircle: The square can be circumscribed by a circle, with the circle's diameter equal to the diagonal of the square.
- Incircle: A circle can be inscribed within the square, touching the midpoint of each side, with the circle's radius equal to half the side length.
Squares are also classified under different categories of quadrilaterals:
- Rectangle: Since all angles are right angles, a square is a special type of rectangle.
- Rhombus: With all sides equal, a square is also a type of rhombus.
- Parallelogram: Opposite sides of a square are parallel, fitting the definition of a parallelogram.
These properties make squares highly symmetrical and fundamental in geometry, often serving as a basis for understanding more complex geometric concepts.
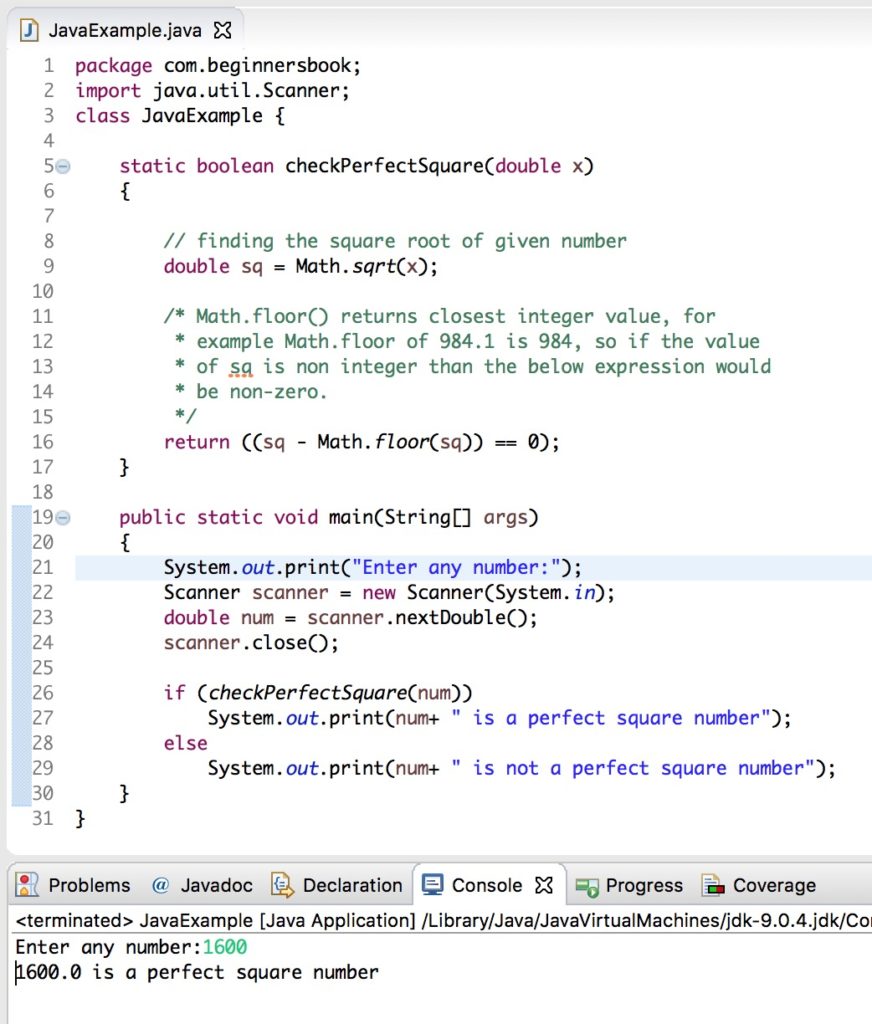
Square Roots and Their Calculation
Understanding square roots is fundamental in mathematics, especially when dealing with various calculations and problem-solving scenarios. The square root of a number \( x \) is a value that, when multiplied by itself, equals \( x \). This is denoted as \( \sqrt{x} \). Let's delve into the details of calculating square roots, both for perfect squares and non-perfect squares.
Perfect Squares
Perfect squares are numbers that are the square of an integer. For instance:
- \(\sqrt{81} = 9\) because \(9 \times 9 = 81\)
- \(\sqrt{144} = 12\) because \(12 \times 12 = 144\)
- \(\sqrt{625} = 25\) because \(25 \times 25 = 625\)
Non-Perfect Squares
For numbers that are not perfect squares, their square roots are irrational numbers. For example:
- \(\sqrt{2} \approx 1.414\)
- \(\sqrt{3} \approx 1.732\)
- \(\sqrt{5} \approx 2.236\)
Calculation Methods
Prime Factorization
One method to find the square root is by prime factorization. For example, to find the square root of 324:
Prime factors: \(324 = 2 \times 2 \times 3 \times 3 \times 3 \times 3\)
Square root: \(\sqrt{324} = 2 \times 3 \times 3 = 18\)
Repeated Subtraction Method
This method involves subtracting consecutive odd numbers from the target number until zero is reached. For instance, to find \(\sqrt{121}\):
- 121 - 1 = 120
- 120 - 3 = 117
- 117 - 5 = 112
- 112 - 7 = 105
- 105 - 9 = 96
- 96 - 11 = 85
- 85 - 13 = 72
- 72 - 15 = 57
- 57 - 17 = 40
- 40 - 19 = 21
- 21 - 21 = 0
Thus, \(\sqrt{121} = 11\).
Long Division Method
The long division method is another systematic way to find square roots. For example, to find the square root of 104976:
- Separate the digits: 10,49,76
- Find the largest number whose square is less than or equal to 10: \(3 \times 3 = 9\)
- Subtract and bring down the next pair of digits, then repeat the process.
Continuing this process, we find that \(\sqrt{104976} = 324\).
Estimation Method
This involves guessing and checking:
- Start with a number and square it.
- Adjust the guess based on whether the squared value is higher or lower than the target number.
- Refine the guess until the square root is found.
Understanding these methods and practicing them will enhance your mathematical skills and help you tackle various problems involving square roots efficiently.
Mathematical Patterns and Properties
The study of mathematical patterns and properties involving squares reveals intriguing concepts that are foundational to various branches of mathematics. Squares, characterized by their equal sides and right angles, exhibit unique properties that make them essential in geometry, algebra, and number theory.
Here are some key aspects:
- Geometric Properties
- A square has four equal sides and four right angles.
- Diagonals of a square bisect each other at right angles and are equal in length.
- The area of a square is calculated as \(A = s^2\), where \(s\) is the length of a side.
- Algebraic Patterns
- Squares of integers produce perfect square numbers (e.g., \(1, 4, 9, 16\)).
- The difference of squares formula: \(a^2 - b^2 = (a+b)(a-b)\).
- Number Theory
- Magic squares, where the sums of numbers in each row, column, and diagonal are the same.
- Benjamin Franklin’s magic square of squares, a 16x16 grid with unique properties.
Understanding these properties helps in recognizing patterns and solving complex problems, showcasing the beauty and utility of squares in mathematics.

Applications in Algebra
In algebra, squares have numerous applications, particularly in solving equations, factoring, and understanding polynomial expressions.
One fundamental application involves solving quadratic equations. A quadratic equation in the form \(ax^2 + bx + c = 0\) can often be solved by taking the square root of both sides or by factoring it into the product of two binomials.
Furthermore, squares play a significant role in factoring polynomials. The process of factoring involves expressing a polynomial as the product of its factors, which often includes identifying perfect square factors.
Moreover, squares are essential in understanding and manipulating polynomial expressions. For instance, the difference of squares is a common algebraic pattern that arises when expanding or factoring certain polynomial expressions.
In summary, squares are indispensable in algebra, facilitating the solution of equations, factoring polynomials, and understanding various algebraic expressions and patterns.
Difference of Squares
The difference of squares is a fundamental algebraic pattern that arises when multiplying or factoring expressions consisting of two perfect square terms.
Mathematically, the difference of squares can be expressed as:
This formula demonstrates that the difference of two squares \(a^2\) and \(b^2\) can be factored into the product of two binomials, where the first binomial is the sum of the square roots of the terms, and the second binomial is their difference.
For example, consider the expression \(x^2 - 9\). By recognizing it as a difference of squares, we can factor it as:
Similarly, expressions like \(4y^2 - 16\) or \(25 - 9x^2\) can also be factored using the difference of squares pattern.
This algebraic pattern is not only useful for simplifying expressions but also for solving equations and understanding the structure of polynomial expressions.
Practical Applications in Quilting
Quilting, a centuries-old craft, finds practical applications for squares in various ways, showcasing the versatility of this geometric shape in textile arts.
One common use of squares in quilting is in the creation of patchwork quilts. Quilters often cut fabric into square pieces of equal size and sew them together to form intricate designs and patterns.
Squares can also be combined with other geometric shapes such as triangles and rectangles to create visually appealing quilt blocks. These blocks can then be arranged in different layouts to achieve different overall quilt designs.
Furthermore, the precise nature of squares makes them ideal for creating geometric patterns and symmetrical arrangements within quilts. Quilters often use squares as building blocks for more complex designs, such as tessellations and medallion quilts.
Additionally, squares are useful for creating borders and frames around quilt blocks, providing structure and visual interest to the finished quilt top.
Overall, squares play a vital role in the art of quilting, offering endless possibilities for creativity and expression through the arrangement and manipulation of fabric pieces.
Educational Resources for Class 8
Class 8 students often explore a variety of mathematical concepts, including squares and their properties. Here are some comprehensive resources and activities to help students understand and master these topics:
- Interactive Lessons: Utilize online platforms that offer interactive lessons on squares, square roots, and related properties. These platforms often include visual aids and practice problems to enhance understanding.
- Worksheets: Provide students with printable worksheets that cover a range of problems, from basic square calculations to more complex applications in algebra and geometry.
- Educational Videos: Incorporate educational videos that explain the concepts of squares and square roots. These videos can include animations and real-world examples to make learning more engaging.
- Math Games: Introduce math games that focus on squares and their properties. These games can help reinforce concepts through fun and interactive challenges.
- Quizzes and Tests: Regular quizzes and tests can help assess students' understanding of squares. Online platforms often offer customizable quizzes that can be tailored to individual learning needs.
- Group Activities: Organize group activities where students work together to solve square-related problems. This encourages collaboration and peer learning.
- Real-World Applications: Discuss real-world applications of squares, such as in architecture, engineering, and technology, to show the practical relevance of the concepts learned.
Sample Problems
Here are some sample problems to help students practice:
- Simplify the following:
- \(\sqrt{49}\)
- \(\sqrt{81}\)
- \(\sqrt{121}\)
- Calculate the area of a square with a side length of 7 cm.
- If the perimeter of a square is 36 cm, find the length of one side.
- Solve the equation: \(x^2 = 64\)
Useful Websites
Here are some websites that offer valuable resources for learning about squares:
| Resource Type | Description |
|---|---|
| Interactive Lessons | Engage students with interactive content that includes visual aids and practice problems. |
| Worksheets | Printable materials covering a range of problems for hands-on practice. |
| Educational Videos | Videos with animations and real-world examples to enhance understanding. |
| Math Games | Interactive games that reinforce concepts through fun challenges. |
| Quizzes and Tests | Customizable quizzes for assessing understanding and progress. |
| Group Activities | Collaborative problem-solving to encourage peer learning. |
| Real-World Applications | Examples of how squares are used in various fields. |

Advanced Mathematical Concepts Involving Squares
Advanced mathematical concepts involving squares delve into intricate theories and applications that span various branches of mathematics. Let's explore some of these fascinating ideas:
- Diophantine Equations: Diophantine equations are polynomial equations with integer coefficients, and solutions sought are also integers. Advanced techniques involving squares often play a crucial role in solving these equations.
- Fermat's Last Theorem: This famous conjecture, proven by Andrew Wiles in 1994, states that no three positive integers a, b, and c can satisfy the equation \(a^n + b^n = c^n\) for any integer value of n greater than 2. The proof heavily relies on modular forms, elliptic curves, and properties of squares.
- Number Theory: Squares are central to many concepts in number theory, including quadratic residues, quadratic reciprocity, and the distribution of primes. Advanced topics like the Generalized Riemann Hypothesis involve complex interplays of squares with other mathematical structures.
- Geometry: Advanced geometric concepts often utilize squares in profound ways. This includes topics such as the Pythagorean theorem, geometric constructions, and higher-dimensional analogs like the tesseract in four-dimensional geometry.
- Matrix Theory: Matrices with square dimensions have unique properties and applications in various fields, including computer science, quantum mechanics, and cryptography. Advanced matrix theory explores eigenvalues, eigenvectors, and applications in optimization and machine learning.
Xem video để tìm hiểu cách tính số lượng hình vuông trên một bàn cờ 8×8 và tham gia vào cuộc thi toán học thú vị!
Bao nhiêu Hình Vuông trên Bàn Cờ 8×8? [CUỘC THI TOÁN HỌC]
READ MORE:
Xem video để học cách gắn kết các hình vuông đầu tiên của bạn vào một chăn thảm đan Granny Square và tham gia cùng chúng tôi!
Chăn Thảm Bằng Cách Đan Granny Square Phần 3 - Gắn Kết 8 Hình Vuông Đầu Tiên Của Bạn