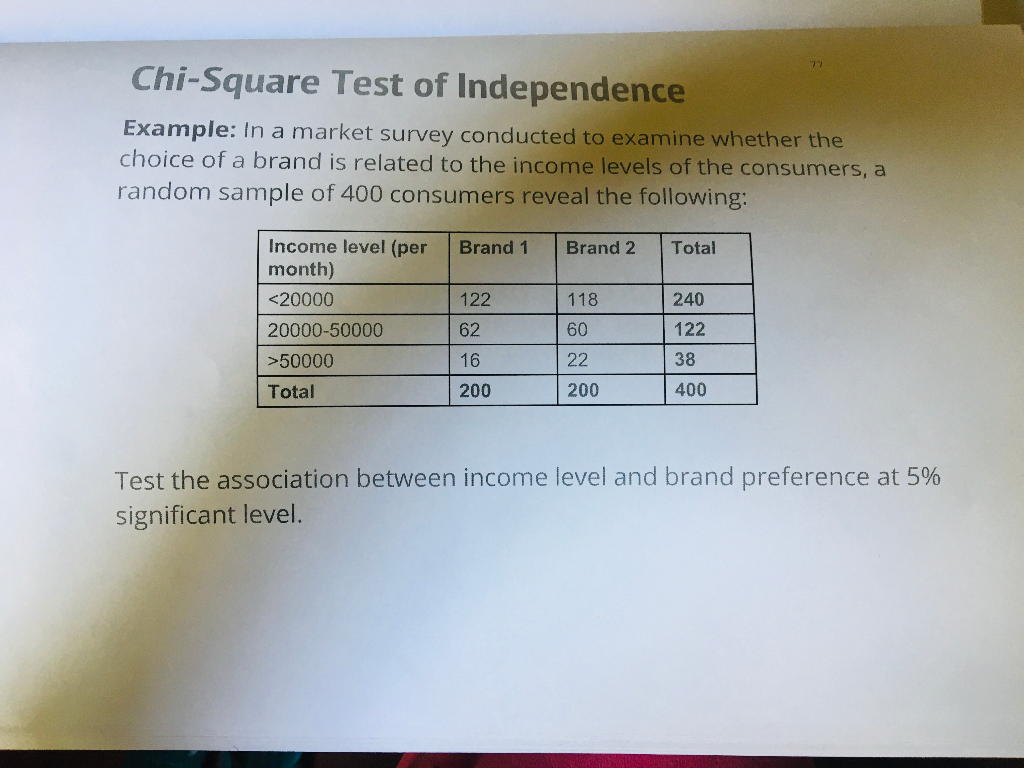
Topic chi square test examples with solutions: Discover comprehensive chi-square test examples with solutions that simplify statistical analysis. Our guide covers everything from basic concepts to detailed, step-by-step solutions, helping you understand and apply chi-square tests effectively. Whether you're a student or a professional, these examples will enhance your analytical skills and boost your confidence in interpreting data.
Table of Content
- Chi-Square Test Examples with Solutions
- Introduction to Chi-Square Test
- Types of Chi-Square Tests
- Steps to Perform a Chi-Square Test
- Chi-Square Test for Independence: Examples and Solutions
- Chi-Square Goodness of Fit Test: Examples and Solutions
- Interpreting Chi-Square Test Results
- Common Mistakes and How to Avoid Them
- Applications of Chi-Square Test in Different Fields
- Conclusion and Summary
- YOUTUBE:
Chi-Square Test Examples with Solutions
The chi-square test is a statistical test used to determine if a significant relationship exists between categorical variables. Below are detailed examples with solutions.
Example 1: Chi-Square Test for Independence
Suppose a researcher wants to determine if there is an association between gender (male and female) and voting preference (Party A and Party B).
The data collected is as follows:
| Party A | Party B | Total | |
|---|---|---|---|
| Male | 30 | 20 | 50 |
| Female | 20 | 30 | 50 |
| Total | 50 | 50 | 100 |
To test for independence, we calculate the expected frequencies.
The formula for expected frequency is:
\[ E_{ij} = \frac{(Row\ Total) \times (Column\ Total)}{Grand\ Total} \]
For Male voting for Party A:
\[ E_{11} = \frac{50 \times 50}{100} = 25 \]
For Male voting for Party B:
\[ E_{12} = \frac{50 \times 50}{100} = 25 \]
For Female voting for Party A:
\[ E_{21} = \frac{50 \times 50}{100} = 25 \]
For Female voting for Party B:
\[ E_{22} = \frac{50 \times 50}{100} = 25 \]
Next, we calculate the chi-square statistic:
\[ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \]
Where \( O_{ij} \) is the observed frequency and \( E_{ij} \) is the expected frequency.
Substituting the values:
\[ \chi^2 = \frac{(30-25)^2}{25} + \frac{(20-25)^2}{25} + \frac{(20-25)^2}{25} + \frac{(30-25)^2}{25} \]
\[ \chi^2 = \frac{25}{25} + \frac{25}{25} + \frac{25}{25} + \frac{25}{25} = 4 \]
With 1 degree of freedom, the critical value at 0.05 significance level is 3.841. Since 4 > 3.841, we reject the null hypothesis and conclude that there is an association between gender and voting preference.
Example 2: Chi-Square Goodness of Fit Test
Suppose a dice manufacturer wants to test if a six-sided die is fair. The expected frequency for each face (1 to 6) should be equal if the die is fair.
The observed frequencies after 60 rolls are:
- Face 1: 8
- Face 2: 12
- Face 3: 10
- Face 4: 9
- Face 5: 11
- Face 6: 10
The expected frequency for each face is:
\[ E = \frac{Total\ Rolls}{Number\ of\ Faces} = \frac{60}{6} = 10 \]
Next, we calculate the chi-square statistic:
\[ \chi^2 = \sum \frac{(O_i - E)^2}{E} \]
Where \( O_i \) is the observed frequency for each face.
Substituting the values:
\[ \chi^2 = \frac{(8-10)^2}{10} + \frac{(12-10)^2}{10} + \frac{(10-10)^2}{10} + \frac{(9-10)^2}{10} + \frac{(11-10)^2}{10} + \frac{(10-10)^2}{10} \]
\[ \chi^2 = \frac{4}{10} + \frac{4}{10} + 0 + \frac{1}{10} + \frac{1}{10} + 0 = 1 \]
With 5 degrees of freedom, the critical value at 0.05 significance level is 11.070. Since 1 < 11.070, we fail to reject the null hypothesis and conclude that the die is fair.

READ MORE:
Introduction to Chi-Square Test
The chi-square test is a statistical method used to determine if there is a significant association between categorical variables. It helps in understanding if observed frequencies differ from expected frequencies based on a specific hypothesis. Chi-square tests are widely used in various fields, including social sciences, biology, and marketing, to analyze survey data, experiment results, and more.
There are two main types of chi-square tests:
- Chi-Square Test for Independence
- Chi-Square Goodness of Fit Test
Chi-Square Test for Independence
This test is used to determine if there is a significant association between two categorical variables. It examines the distribution of sample categorical data to assess if the variables are independent.
Steps to perform a Chi-Square Test for Independence:
- Formulate the null and alternative hypotheses.
- Create a contingency table to display the frequencies of different combinations of variables.
- Calculate the expected frequencies for each cell of the table.
- Compute the chi-square statistic using the formula: \[ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \] where \(O_{ij}\) is the observed frequency and \(E_{ij}\) is the expected frequency.
- Determine the degrees of freedom (df) using the formula: \[ df = (number\ of\ rows - 1) \times (number\ of\ columns - 1) \]
- Compare the calculated chi-square statistic with the critical value from the chi-square distribution table at a chosen significance level (e.g., 0.05).
- Make a decision: If the calculated value is greater than the critical value, reject the null hypothesis, indicating a significant association between the variables.
Chi-Square Goodness of Fit Test
This test determines if a sample data matches an expected distribution. It's used to see if a sample conforms to a hypothesized distribution, such as a uniform distribution.
Steps to perform a Chi-Square Goodness of Fit Test:
- Formulate the null and alternative hypotheses.
- Calculate the expected frequency for each category, usually based on a theoretical distribution.
- Compute the chi-square statistic using the formula: \[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \] where \(O_i\) is the observed frequency and \(E_i\) is the expected frequency.
- Determine the degrees of freedom (df) using the formula: \[ df = number\ of\ categories - 1 \]
- Compare the calculated chi-square statistic with the critical value from the chi-square distribution table at a chosen significance level (e.g., 0.05).
- Make a decision: If the calculated value is greater than the critical value, reject the null hypothesis, indicating that the sample data does not fit the expected distribution.
Types of Chi-Square Tests
Chi-square tests are non-parametric statistical tests used to determine if there is a significant association between categorical variables or if a sample data fits an expected distribution. There are two main types of chi-square tests:
1. Chi-Square Test for Independence
The chi-square test for independence assesses whether two categorical variables are independent or related. It is often used in contingency tables to analyze survey or experimental data.
Steps to perform a Chi-Square Test for Independence:
- Formulate Hypotheses:
- Null Hypothesis (\(H_0\)): The two variables are independent.
- Alternative Hypothesis (\(H_1\)): The two variables are not independent.
- Construct a contingency table to display the observed frequencies for each combination of categories.
- Calculate the expected frequencies for each cell of the table using the formula: \[ E_{ij} = \frac{(Row\ Total) \times (Column\ Total)}{Grand\ Total} \]
- Compute the chi-square statistic using the formula: \[ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \] where \(O_{ij}\) is the observed frequency and \(E_{ij}\) is the expected frequency.
- Determine the degrees of freedom (df) using the formula: \[ df = (number\ of\ rows - 1) \times (number\ of\ columns - 1) \]
- Compare the calculated chi-square statistic with the critical value from the chi-square distribution table at a chosen significance level (e.g., 0.05).
- Make a decision: If the calculated value is greater than the critical value, reject the null hypothesis, indicating a significant association between the variables.
2. Chi-Square Goodness of Fit Test
The chi-square goodness of fit test determines if a sample data fits a specified distribution. It is commonly used to see if a sample matches an expected distribution, such as a uniform distribution.
Steps to perform a Chi-Square Goodness of Fit Test:
- Formulate Hypotheses:
- Null Hypothesis (\(H_0\)): The observed frequencies fit the expected distribution.
- Alternative Hypothesis (\(H_1\)): The observed frequencies do not fit the expected distribution.
- Calculate the expected frequency for each category based on the theoretical distribution.
- Compute the chi-square statistic using the formula: \[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \] where \(O_i\) is the observed frequency and \(E_i\) is the expected frequency.
- Determine the degrees of freedom (df) using the formula: \[ df = number\ of\ categories - 1 \]
- Compare the calculated chi-square statistic with the critical value from the chi-square distribution table at a chosen significance level (e.g., 0.05).
- Make a decision: If the calculated value is greater than the critical value, reject the null hypothesis, indicating that the sample data does not fit the expected distribution.
Steps to Perform a Chi-Square Test
Performing a chi-square test involves several systematic steps to ensure accurate results. Here are the detailed steps to perform both the Chi-Square Test for Independence and the Chi-Square Goodness of Fit Test:
Chi-Square Test for Independence
This test is used to determine if there is a significant association between two categorical variables.
- Formulate Hypotheses:
- Null Hypothesis (\(H_0\)): The two variables are independent.
- Alternative Hypothesis (\(H_1\)): The two variables are not independent.
- Collect Data and Create a Contingency Table:
Organize the data into a contingency table, displaying the observed frequencies for each combination of categories.
Category 1 Category 2 ... Total Observed 1 Observed 2 ... Row Total Observed 3 Observed 4 ... Row Total Column Total Column Total ... Grand Total - Calculate Expected Frequencies:
Use the formula to calculate the expected frequency for each cell:
\[
E_{ij} = \frac{(Row\ Total) \times (Column\ Total)}{Grand\ Total}
\] - Compute the Chi-Square Statistic:
Calculate the chi-square statistic using the formula:
\[
\chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}}
\]where \(O_{ij}\) is the observed frequency and \(E_{ij}\) is the expected frequency.
- Determine Degrees of Freedom:
Calculate the degrees of freedom (df) using the formula:
\[
df = (number\ of\ rows - 1) \times (number\ of\ columns - 1)
\] - Compare with Critical Value:
Refer to the chi-square distribution table to find the critical value at a chosen significance level (e.g., 0.05). Compare the calculated chi-square statistic to this critical value.
- Make a Decision:
If the calculated chi-square statistic is greater than the critical value, reject the null hypothesis. This indicates a significant association between the variables.
Chi-Square Goodness of Fit Test
This test is used to determine if a sample data fits a specified distribution.
- Formulate Hypotheses:
- Null Hypothesis (\(H_0\)): The observed frequencies fit the expected distribution.
- Alternative Hypothesis (\(H_1\)): The observed frequencies do not fit the expected distribution.
- Collect Data:
Gather the observed frequencies for each category.
- Calculate Expected Frequencies:
Determine the expected frequency for each category based on the theoretical distribution.
- Compute the Chi-Square Statistic:
Calculate the chi-square statistic using the formula:
\[
\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}
\]where \(O_i\) is the observed frequency and \(E_i\) is the expected frequency.
- Determine Degrees of Freedom:
Calculate the degrees of freedom (df) using the formula:
\[
df = number\ of\ categories - 1
\] - Compare with Critical Value:
Refer to the chi-square distribution table to find the critical value at a chosen significance level (e.g., 0.05). Compare the calculated chi-square statistic to this critical value.
- Make a Decision:
If the calculated chi-square statistic is greater than the critical value, reject the null hypothesis. This indicates that the sample data does not fit the expected distribution.
Chi-Square Test for Independence: Examples and Solutions
The Chi-Square Test for Independence is used to determine whether there is a significant association between two categorical variables. Here, we explore two examples to illustrate how this test is applied.
Example 1: Gender and Voting Preference
Suppose a survey was conducted to understand if there is an association between gender and voting preference. The results are summarized in the contingency table below:
| Prefer Candidate A | Prefer Candidate B | Total | |
|---|---|---|---|
| Male | 40 | 30 | 70 |
| Female | 20 | 40 | 60 |
| Total | 60 | 70 | 130 |
- Formulate Hypotheses:
- Null Hypothesis (\(H_0\)): There is no association between gender and voting preference.
- Alternative Hypothesis (\(H_A\)): There is an association between gender and voting preference.
- Calculate Expected Frequencies:
Expected frequency for each cell is calculated using the formula:
\[
E_{ij} = \frac{(Row\ Total)_i \times (Column\ Total)_j}{Grand\ Total}
\]- Expected frequency for Male and Candidate A: \(\frac{70 \times 60}{130} \approx 32.31\)
- Expected frequency for Male and Candidate B: \(\frac{70 \times 70}{130} \approx 37.69\)
- Expected frequency for Female and Candidate A: \(\frac{60 \times 60}{130} \approx 27.69\)
- Expected frequency for Female and Candidate B: \(\frac{60 \times 70}{130} \approx 32.31\)
- Compute Chi-Square Statistic:
The Chi-Square statistic (\(\chi^2\)) is calculated as:
\[
\chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}}
\]- \(\chi^2 = \frac{(40 - 32.31)^2}{32.31} + \frac{(30 - 37.69)^2}{37.69} + \frac{(20 - 27.69)^2}{27.69} + \frac{(40 - 32.31)^2}{32.31} \approx 7.46\)
- Determine Degrees of Freedom:
Degrees of freedom (df) are calculated as:
\[
df = (Number\ of\ Rows - 1) \times (Number\ of\ Columns - 1)
\]- For our table, df = \((2-1) \times (2-1) = 1\)
- Compare with Critical Value:
Using a significance level (\(\alpha\)) of 0.05, the critical value from the Chi-Square distribution table with 1 degree of freedom is 3.841. Since 7.46 > 3.841:
- Make a Decision:
Reject the null hypothesis. There is evidence to suggest an association between gender and voting preference.
Example 2: Education Level and Job Satisfaction
A company conducted a study to investigate if job satisfaction is related to the education level of employees. The data collected is presented in the table below:
| Satisfied | Neutral | Unsatisfied | Total | |
|---|---|---|---|---|
| High School | 20 | 15 | 10 | 45 |
| Bachelor's | 30 | 25 | 15 | 70 |
| Master's | 25 | 20 | 10 | 55 |
| Total | 75 | 60 | 35 | 170 |
- Formulate Hypotheses:
- Null Hypothesis (\(H_0\)): There is no association between education level and job satisfaction.
- Alternative Hypothesis (\(H_A\)): There is an association between education level and job satisfaction.
- Calculate Expected Frequencies:
- Expected frequency for High School and Satisfied: \(\frac{45 \times 75}{170} \approx 19.85\)
- Expected frequency for High School and Neutral: \(\frac{45 \times 60}{170} \approx 15.88\)
- Expected frequency for High School and Unsatisfied: \(\frac{45 \times 35}{170} \approx 9.26\)
- Expected frequency for Bachelor's and Satisfied: \(\frac{70 \times 75}{170} \approx 30.88\)
- Expected frequency for Bachelor's and Neutral: \(\frac{70 \times 60}{170} \approx 24.71\)
- Expected frequency for Bachelor's and Unsatisfied: \(\frac{70 \times 35}{170} \approx 14.41\)
- Expected frequency for Master's and Satisfied: \(\frac{55 \times 75}{170} \approx 24.26\)
- Expected frequency for Master's and Neutral: \(\frac{55 \times 60}{170} \approx 19.41\)
- Expected frequency for Master's and Unsatisfied: \(\frac{55 \times 35}{170} \approx 11.32\)
- Compute Chi-Square Statistic:
- \(\chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\)
- \(\chi^2 \approx \frac{(20 - 19.85)^2}{19.85} + \frac{(15 - 15.88)^2}{15.88} + \frac{(10 - 9.26)^2}{9.26} + \frac{(30 - 30.88)^2}{30.88} + \frac{(25 - 24.71)^2}{24.71} + \frac{(15 - 14.41)^2}{14.41} + \frac{(25 - 24.26)^2}{24.26} + \frac{(20 - 19.41)^2}{19.41} + \frac{(10 - 11.32)^2}{11.32} \approx 0.24\)
- Determine Degrees of Freedom:
- df = \((3-1) \times (3-1) = 4\)
- Compare with Critical Value:
- At \(\alpha = 0.05\), the critical value for df = 4 is 9.488. Since 0.24 < 9.488:
- Make a Decision:
Fail to reject
the null hypothesis. There is no significant association between education level and job satisfaction.

Chi-Square Goodness of Fit Test: Examples and Solutions
The Chi-Square Goodness of Fit Test is used to determine if a sample data matches a population with a specific distribution. Here, we provide two detailed examples to illustrate how this test is performed.
Example 1: Fairness of a Die
We want to test if a six-sided die is fair. We roll the die 60 times and record the frequency of each face:
| Face | Observed Frequency |
|---|---|
| 1 | 8 |
| 2 | 12 |
| 3 | 9 |
| 4 | 10 |
| 5 | 11 |
| 6 | 10 |
-
Formulate Hypotheses:
- Null Hypothesis \(H_0\): The die is fair, i.e., each face has an equal probability of \( \frac{1}{6} \).
- Alternative Hypothesis \(H_a\): The die is not fair.
-
Calculate Expected Frequencies:
Since the die is fair, the expected frequency for each face is \( \frac{60}{6} = 10 \).
-
Compute Chi-Square Statistic:
We use the formula:
\[
\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}
\]Where \( O_i \) is the observed frequency and \( E_i \) is the expected frequency.
Calculations:
\[
\chi^2 = \frac{(8-10)^2}{10} + \frac{(12-10)^2}{10} + \frac{(9-10)^2}{10} + \frac{(10-10)^2}{10} + \frac{(11-10)^2}{10} + \frac{(10-10)^2}{10}
\]\[
\chi^2 = \frac{4}{10} + \frac{4}{10} + \frac{1}{10} + \frac{0}{10} + \frac{1}{10} + \frac{0}{10} = 1
\] -
Determine Degrees of Freedom:
Degrees of freedom \(df = n - 1 = 6 - 1 = 5\).
-
Compare with Critical Value:
For \(df = 5\) and \( \alpha = 0.05 \), the critical value from the chi-square distribution table is 11.07.
-
Make a Decision:
Since 1 < 11.07, we fail to reject the null hypothesis. There is no evidence to suggest that the die is not fair.
Example 2: Distribution of M&M Colors
A company claims that the distribution of M&M colors in a bag is as follows: 30% brown, 20% yellow, 20% red, 10% blue, 10% green, and 10% orange. We want to test this claim with a sample of 100 M&Ms:
| Color | Observed Frequency | Expected Frequency |
|---|---|---|
| Brown | 32 | 30 |
| Yellow | 18 | 20 |
| Red | 22 | 20 |
| Blue | 8 | 10 |
| Green | 10 | 10 |
| Orange | 10 | 10 |
-
Formulate Hypotheses:
- Null Hypothesis \(H_0\): The distribution of M&M colors matches the claimed distribution.
- Alternative Hypothesis \(H_a\): The distribution of M&M colors does not match the claimed distribution.
-
Calculate Expected Frequencies:
The expected frequencies are given as per the claimed distribution for a sample of 100 M&Ms.
-
Compute Chi-Square Statistic:
We use the formula:
\[
\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}
\]Calculations:
\[
\chi^2 = \frac{(32-30)^2}{30} + \frac{(18-20)^2}{20} + \frac{(22-20)^2}{20} + \frac{(8-10)^2}{10} + \frac{(10-10)^2}{10} + \frac{(10-10)^2}{10}
\]\[
\chi^2 = \frac{4}{30} + \frac{4}{20} + \frac{4}{20} + \frac{4}{10} + \frac{0}{10} + \frac{0}{10} = 0.133 + 0.2 + 0.2 + 0.4 + 0 + 0 = 0.933
\] -
Determine Degrees of Freedom:
Degrees of freedom \(df = n - 1 = 6 - 1 = 5\).
-
Compare with Critical Value:
For \(df = 5\) and \( \alpha = 0.05 \), the critical value from the chi-square distribution table is 11.07.
-
Make a Decision:
Since 0.933 < 11.07, we fail to reject the null hypothesis. There is no evidence to suggest that the distribution of M&M colors does not match the claimed distribution.
Interpreting Chi-Square Test Results
Interpreting the results of a Chi-Square test involves understanding several key concepts such as the Chi-Square statistic, degrees of freedom, p-values, and significance levels. Here's a step-by-step guide to help you interpret these results:
1. Chi-Square Statistic
The Chi-Square statistic (\(\chi^2\)) is calculated using the formula:
\[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \]
where \(O_i\) is the observed frequency and \(E_i\) is the expected frequency. The Chi-Square statistic measures the discrepancy between the observed and expected frequencies. A higher value indicates a larger discrepancy.
2. Degrees of Freedom
The degrees of freedom (df) for a Chi-Square test depend on the number of categories in the data. For a test of independence, the degrees of freedom are calculated as:
\[ df = (r - 1) \times (c - 1) \]
where \(r\) is the number of rows and \(c\) is the number of columns in the contingency table.
3. P-Value
The p-value indicates the probability that the observed data could have occurred under the null hypothesis. It is derived from the Chi-Square distribution with the calculated degrees of freedom. The p-value helps in deciding whether to reject the null hypothesis.
4. Significance Level
The significance level (\(\alpha\)) is the threshold for rejecting the null hypothesis. Commonly used levels are 0.05, 0.01, and 0.001. If the p-value is less than or equal to the significance level, the null hypothesis is rejected.
5. Making a Decision
To interpret the results:
- Calculate the Chi-Square statistic using the observed and expected frequencies.
- Determine the degrees of freedom for your test.
- Find the critical value from the Chi-Square distribution table corresponding to your degrees of freedom and significance level.
- Compare the Chi-Square statistic to the critical value:
- If \(\chi^2\) is greater than the critical value, reject the null hypothesis.
- If \(\chi^2\) is less than or equal to the critical value, do not reject the null hypothesis.
Example Interpretation
Let's consider an example where we test if there is an association between gender and voting preference. We have the following observed frequencies:
| Republican | Democrat | Independent | Total | |
| Male | 100 | 70 | 30 | 200 |
| Female | 140 | 60 | 20 | 220 |
| Total | 240 | 130 | 50 | 440 |
The expected frequencies are calculated as:
| Republican | Democrat | Independent | |
| Male | 109 | 59 | 22.72 |
| Female | 120 | 65 | 25 |
Using these, we calculate the Chi-Square statistic:
\[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} = 0.743 + 2.050 + 2.332 + 3.333 + 0.384 + 1 = 9.837 \]
With 2 degrees of freedom, the critical value at \(\alpha = 0.05\) is 5.991. Since 9.837 > 5.991, we reject the null hypothesis and conclude that there is an association between gender and voting preference.
Common Mistakes and How to Avoid Them
The Chi-Square Test is a powerful statistical tool, but there are common mistakes that can lead to incorrect conclusions. Here are some of the most frequent errors and how to avoid them:
-
Using Non-Categorical Data:
The Chi-Square Test is designed for categorical data. Applying it to continuous data is inappropriate. Ensure your data is categorical, meaning it is divided into distinct categories or groups.
-
Small Sample Sizes:
Chi-Square Tests require a sufficiently large sample size to be valid. Small sample sizes can lead to inaccurate results. A general rule of thumb is that each expected frequency should be at least 5.
-
Ignoring Assumptions:
Make sure the assumptions of the Chi-Square Test are met:
- Independence of observations: Each observation should be independent of others.
- Expected frequency should be sufficiently large (usually at least 5 in each cell of the contingency table).
-
Misinterpreting P-Values:A p-value indicates the probability of observing the data if the null hypothesis is true. It does not measure the strength or importance of an effect. A low p-value suggests that the observed data is unlikely under the null hypothesis, leading to its rejection.
-
Overlooking Effect Size:
Significance tests do not indicate the size or importance of an effect. Consider using measures of effect size, such as Cramer's V or the Phi coefficient, to understand the strength of the relationship.
-
Incorrect Calculation of Expected Frequencies:
Expected frequencies should be calculated correctly using the formula:
\[ E_{ij} = \frac{(Row \ Total \times Column \ Total)}{Grand \ Total} \]
Errors in this calculation can lead to incorrect conclusions. -
Multiple Comparisons Problem:
Conducting multiple Chi-Square Tests on the same data set increases the risk of Type I errors (false positives). Apply corrections such as the Bonferroni correction to adjust for multiple comparisons.
By being aware of these common mistakes and taking steps to avoid them, you can ensure the validity and reliability of your Chi-Square Test results.
Applications of Chi-Square Test in Different Fields
The Chi-Square test is a versatile statistical tool widely used across various fields to analyze categorical data. Here are some key applications:
- Genetics: The Chi-Square test is commonly used to analyze Mendelian inheritance patterns. Researchers use it to determine if observed genetic crosses align with expected ratios, aiding in the understanding of gene expression and inheritance mechanisms.
- Market Research: Businesses use the Chi-Square test to understand consumer behavior and preferences. By comparing observed customer responses against expected outcomes, companies can tailor their marketing strategies and product offerings to better meet market demands.
- Sociology: Sociologists apply the Chi-Square test to examine relationships between categorical variables in social research, such as studies on demographic factors, social trends, and the impact of societal interventions.
- Medicine and Public Health: The test is instrumental in medical research for analyzing the efficacy of treatments or the distribution of health-related conditions across different populations, contributing to improved public health policies and interventions.
- Education: In educational research, the Chi-Square test helps assess the relationship between educational methods and learning outcomes, or explore the association between demographic factors and educational achievements.
- Quality Control: In manufacturing and quality assurance, the Chi-Square test assesses the conformity of product defects or failures to expected distributions, enabling companies to maintain quality standards and improve production processes.
Here are detailed steps to apply the Chi-Square test in these fields:
- Formulate Hypotheses: Define the null hypothesis (e.g., there is no association between the variables) and the alternative hypothesis (e.g., there is an association).
- Collect Data: Gather observed data and categorize it into a contingency table format.
- Calculate Expected Frequencies: Based on the null hypothesis, compute the expected frequencies for each category.
- Compute Chi-Square Statistic: Use the formula \(\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}\), where \(O_i\) are the observed frequencies and \(E_i\) are the expected frequencies.
- Determine Degrees of Freedom: Calculate the degrees of freedom for the test, typically \((\text{number of rows} - 1) \times (\text{number of columns} - 1)\).
- Compare with Critical Value: Compare the computed Chi-Square statistic with the critical value from the Chi-Square distribution table at the desired significance level (e.g., 0.05).
- Make a Decision: If the Chi-Square statistic exceeds the critical value, reject the null hypothesis, indicating a significant association between the variables.
The Chi-Square test is a powerful tool for analyzing categorical data, providing insights into the relationships and distributions across various fields.
Conclusion and Summary
The Chi-Square test is a versatile statistical tool used to examine the relationship between categorical variables. It helps in determining whether the observed frequencies in a contingency table significantly differ from the expected frequencies derived under the null hypothesis. There are two main types of Chi-Square tests: the Chi-Square Test for Independence and the Chi-Square Goodness of Fit Test.
In the Chi-Square Test for Independence, we assess whether two categorical variables are independent of each other. This involves calculating the test statistic using the observed and expected frequencies, and then comparing this value to a critical value from the Chi-Square distribution table. If the test statistic exceeds the critical value, we reject the null hypothesis, suggesting a significant association between the variables.
The Chi-Square Goodness of Fit Test is used to determine if a sample data matches a population with a specific distribution. By comparing the observed frequencies with the expected frequencies under the assumed distribution, we can infer if the sample represents the population well or if there are significant deviations.
When interpreting Chi-Square test results, it is crucial to consider the p-value, which indicates the probability of observing the test results under the null hypothesis. A p-value less than the chosen significance level (commonly 0.05) leads to the rejection of the null hypothesis, implying that the observed data do not fit the expected distribution.
Common mistakes in conducting Chi-Square tests include using inappropriate sample sizes, not meeting the test assumptions (such as expected frequencies being too low), and misinterpreting the results. It is important to ensure that the assumptions of the test are satisfied and to understand the context of the data and the hypotheses being tested.
Chi-Square tests have wide applications across various fields such as market research, medical studies, and social sciences. For example, they are used to analyze consumer preferences, study the relationship between treatment and recovery rates in medical research, and investigate sociological phenomena like voting behavior and education level associations.
In summary, the Chi-Square test is a powerful method for analyzing categorical data. By carefully designing the study, ensuring assumptions are met, and correctly interpreting the results, researchers can draw meaningful conclusions about the relationships and distributions within their data.
Kiểm Tra Chi-Square
READ MORE:
Cách... Thực Hiện Kiểm Tra Chi-Square (Bằng Tay)
:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)