Topic square root of 45 in radical form: Discover how to simplify the square root of 45 into its radical form with our step-by-step guide. Learn the prime factorization method, understand the mathematical concepts behind it, and see practical applications. Perfect for students, teachers, and math enthusiasts seeking a clear and concise explanation of the square root of 45 in radical form.
Table of Content
- Square Root of 45 in Radical Form
- Introduction
- Understanding Square Roots
- Prime Factorization Method
- Step-by-Step Simplification
- Simplified Radical Form
- Mathematical Explanation
- Applications of Simplified Square Roots
- Common Mistakes to Avoid
- Practice Problems
- Conclusion
- YOUTUBE: Tìm hiểu cách đơn giản hóa căn bậc hai của 45 và ứng dụng thực tế của nó trong toán học và các lĩnh vực khác. Video này sẽ hướng dẫn bạn từng bước để đạt được kết quả chính xác.
Square Root of 45 in Radical Form
The square root of 45 in its simplest radical form can be found by breaking down the number into its prime factors and simplifying.
Steps to Simplify:
- Factorize 45 into its prime factors: \( 45 = 3^2 \times 5 \).
- Write the square root of the prime factorization: \( \sqrt{45} = \sqrt{3^2 \times 5} \).
- Simplify the square root by taking out the square of the factor: \( \sqrt{3^2 \times 5} = 3\sqrt{5} \).
Thus, the square root of 45 in radical form is:
\(\sqrt{45} = 3\sqrt{5}\)
This is the simplest form of the square root of 45.

READ MORE:
Introduction
The square root of 45 in radical form is an important concept in mathematics, often encountered in algebra and geometry. To simplify the square root of 45, we use the prime factorization method, which helps in breaking down the number into its simplest form. This process not only makes calculations easier but also provides a deeper understanding of the mathematical principles involved. Below, we will explore the detailed steps to simplify the square root of 45 and explain the significance of this radical form.
- Understanding the concept of square roots.
- Prime factorization of 45.
- Applying the prime factorization to simplify the square root.
- Interpreting the simplified radical form.
By the end of this section, you will be able to confidently simplify the square root of 45 and appreciate its applications in various mathematical problems.
Understanding Square Roots
Square roots are fundamental in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because \(4 \times 4 = 16\). The symbol for the square root is \(\sqrt{}\).
Here are some key points to understand square roots better:
- Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). This is written as \(y = \sqrt{x}\).
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For instance, both 4 and -4 are square roots of 16. However, by convention, \(\sqrt{16}\) is taken to mean the positive root, 4.
- Perfect Squares: Numbers like 1, 4, 9, 16, 25, etc., are perfect squares because their square roots are integers.
- Non-Perfect Squares: Numbers like 2, 3, 5, 7, etc., are not perfect squares, and their square roots are irrational numbers, meaning they cannot be expressed as a simple fraction and their decimal representation goes on forever without repeating.
- Radical Form: The square root of a number can often be simplified using its prime factors. For example, \(\sqrt{45}\) can be simplified to \(3\sqrt{5}\) by factoring 45 into \(3^2 \times 5\).
Understanding these basic concepts of square roots is crucial before moving on to more complex operations, such as simplifying square roots in radical form.
Prime Factorization Method
The prime factorization method is an effective way to simplify the square root of a number by breaking it down into its prime factors. This process is especially useful for simplifying square roots that are not perfect squares, like 45. Here is a step-by-step guide to using the prime factorization method to simplify the square root of 45:
-
Find the Prime Factors:
First, we need to find the prime factors of 45. Prime factors are the prime numbers that multiply together to give the original number.
- 45 can be divided by 3 (since 45 is divisible by 3): \( 45 \div 3 = 15 \)
- 15 can also be divided by 3: \( 15 \div 3 = 5 \)
- 5 is a prime number.
So, the prime factorization of 45 is: \( 45 = 3 \times 3 \times 5 = 3^2 \times 5 \).
-
Express Under the Square Root:
Next, we express the square root of 45 using its prime factors:
\( \sqrt{45} = \sqrt{3^2 \times 5} \)
-
Simplify the Square Root:
We simplify the square root by taking the square root of the squared prime factor out of the radical:
\( \sqrt{3^2 \times 5} = 3\sqrt{5} \)
Thus, using the prime factorization method, we have simplified the square root of 45 to its simplest radical form:
\(\sqrt{45} = 3\sqrt{5}\)
This method not only simplifies the computation but also helps in understanding the structure of numbers and their factors.
Step-by-Step Simplification
Simplifying the square root of 45 involves a series of steps that use the prime factorization method. Follow the steps below to simplify \(\sqrt{45}\) into its radical form.
-
Find the Prime Factors:
First, determine the prime factors of 45. This involves breaking down 45 into the smallest prime numbers that multiply to give 45.
- 45 is divisible by 3: \( 45 \div 3 = 15 \)
- 15 is also divisible by 3: \( 15 \div 3 = 5 \)
- 5 is a prime number.
So, the prime factorization of 45 is: \( 45 = 3^2 \times 5 \).
-
Write the Square Root with Prime Factors:
Express the square root of 45 using the prime factors:
\( \sqrt{45} = \sqrt{3^2 \times 5} \)
-
Simplify Inside the Radical:
Simplify the expression under the square root. Since \(3^2\) is a perfect square, it can be taken out of the square root:
\( \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5} \)
-
Extract the Perfect Square:
Take the square root of \(3^2\), which is 3, and multiply it by the remaining square root:
\( \sqrt{3^2} \times \sqrt{5} = 3 \times \sqrt{5} \)
-
Write the Final Simplified Form:
The simplified radical form of \(\sqrt{45}\) is:
\( \sqrt{45} = 3\sqrt{5} \)
By following these steps, we have simplified the square root of 45 to \(3\sqrt{5}\). This method not only simplifies the expression but also provides a clearer understanding of the components of the number.

Simplified Radical Form
The process of simplifying the square root of 45 results in its simplest radical form, which is more concise and easier to work with in mathematical expressions. Here, we explain how the simplified radical form is derived and its significance.
-
Start with the Prime Factorization:
As previously determined, the prime factorization of 45 is:
\( 45 = 3^2 \times 5 \)
-
Express the Square Root:
We write the square root of 45 using its prime factors:
\( \sqrt{45} = \sqrt{3^2 \times 5} \)
-
Simplify the Expression:
To simplify, we take the square root of the perfect square (32) out of the radical:
\( \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5} \)
\( \sqrt{3^2} = 3 \)
So, we have:
\( 3 \times \sqrt{5} \)
-
Write the Simplified Radical Form:
The simplified radical form of the square root of 45 is:
\( \sqrt{45} = 3\sqrt{5} \)
This simplified form, \(3\sqrt{5}\), is the most reduced way to express the square root of 45. It shows that the original number can be broken down into a simpler, more manageable expression without losing its value.
Understanding and using the simplified radical form is useful in various mathematical contexts, including solving equations, evaluating expressions, and performing operations that involve square roots. It allows for easier manipulation and a clearer view of the number's structure.
Mathematical Explanation
To fully understand the square root of 45 in radical form, it is important to delve into the mathematical concepts and reasoning behind the simplification process. Here, we provide a detailed mathematical explanation of simplifying \(\sqrt{45}\).
-
Prime Factorization:
Begin by finding the prime factors of 45. The prime factorization involves expressing 45 as a product of its prime numbers:
\( 45 = 3^2 \times 5 \)
-
Expressing Under the Square Root:
Next, write the square root of 45 using these prime factors:
\( \sqrt{45} = \sqrt{3^2 \times 5} \)
-
Properties of Square Roots:
Utilize the property of square roots that allows the product of square roots to be split into the square root of each factor:
\( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
Applying this property to our expression gives:
\( \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5} \)
-
Simplifying Perfect Squares:
Recognize that the square root of a perfect square (such as \(3^2\)) is just the base number (3 in this case):
\( \sqrt{3^2} = 3 \)
Therefore, we can simplify our expression to:
\( 3 \times \sqrt{5} \)
-
Final Simplified Form:
Combine the results to write the square root of 45 in its simplest radical form:
\( \sqrt{45} = 3\sqrt{5} \)
This step-by-step breakdown shows that \(\sqrt{45}\) can be simplified by identifying and extracting the perfect square factor within the radical. The final expression, \(3\sqrt{5}\), is the simplest radical form of \(\sqrt{45}\), which is easier to work with in various mathematical contexts.
Understanding this process reinforces key mathematical concepts such as prime factorization, properties of square roots, and simplification techniques, providing a deeper insight into the structure and manipulation of numbers.
Applications of Simplified Square Roots
The simplified square root of 45, which is expressed as 3√5, finds numerous practical applications across different fields. Here are some of the key applications:
-
Geometry and Trigonometry:
In geometry, the simplified square root of 45 can be used to find the side lengths of right-angled triangles. For example, if the area of a square is 45 square units, the side length of the square will be 3√5 units. This principle is also applied in trigonometric problems where calculations involve square roots.
-
Physics:
In physics, simplified square roots often appear in formulas and calculations. For instance, if a physics problem involves calculating the length of a vector or the distance between two points in a plane, the square root of 45 might be used if those distances correspond to the hypotenuse of a right triangle with leg lengths involving √45.
-
Engineering:
Engineers frequently use simplified square roots in design and analysis. When calculating load distributions, stress analysis, and other structural parameters, square roots simplify the complex calculations needed for accurate results.
-
Architecture:
Architects use square roots to determine proportions and dimensions. For example, if a room's floor area is 45 square meters, the side length can be simplified to 3√5 meters, which helps in planning and designing spaces accurately.
-
Astronomy:
In astronomy, distances between celestial bodies often involve large numbers where square roots are used. Simplifying these calculations to forms like 3√5 helps in expressing distances and magnitudes more succinctly.
Understanding how to simplify square roots not only aids in academic pursuits but also enhances practical problem-solving skills across various scientific and engineering disciplines. By mastering these concepts, one can tackle a wide array of real-world challenges with greater ease and precision.
Common Mistakes to Avoid
When simplifying square roots, such as the square root of 45, it is easy to make mistakes that can lead to incorrect results. Here are some common mistakes to watch out for and tips on how to avoid them:
-
Incorrect Factorization:
One common mistake is incorrect factorization of the number inside the square root. For example, correctly factorizing 45 as 9 and 5 is crucial for simplification. Incorrectly factorizing can lead to wrong results.
Correct: \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \)
Incorrect: \( \sqrt{45} \neq \sqrt{15 \times 3} \)
-
Forgetting to Simplify Completely:
Another mistake is not simplifying the square root completely. Ensure that all factors are simplified to their smallest radical form.
Example: \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \)
-
Neglecting Both Positive and Negative Roots:
When solving equations involving square roots, remember that both positive and negative roots should be considered. For instance, if \( x^2 = 9 \), then \( x \) can be 3 or -3.
-
Mistaking Square Roots for Linear Functions:
Square roots are not linear functions and cannot be treated as such. The property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \) holds, but \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \).
Correct: \( \sqrt{16 \times 25} = \sqrt{16} \times \sqrt{25} = 4 \times 5 = 20 \)
Incorrect: \( \sqrt{16 + 25} \neq \sqrt{16} + \sqrt{25} \)
-
Misapplying the Order of Operations:
Ensure that you follow the correct order of operations (PEMDAS/BODMAS) when dealing with square roots and other mathematical expressions.
-
Incorrectly Combining Radicals:
Only like radicals can be combined. For instance, \( 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5} \), but \( 3\sqrt{5} + 2\sqrt{3} \) cannot be combined into a single term.
-
Ignoring the Domain of the Square Root Function:
The square root function is only defined for non-negative numbers in the real number system. Ensure that you do not attempt to simplify the square root of a negative number unless you are working within the context of complex numbers.
By being aware of these common mistakes and carefully following the proper steps for simplification, you can avoid errors and ensure your solutions are accurate.
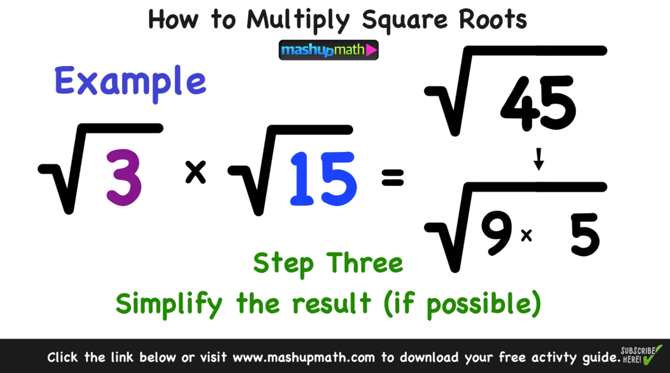
Practice Problems
Practice simplifying square roots to master the concept. Here are some problems to help you get started:
- Simplify the square root of 45: \(\sqrt{45}\)
- Simplify the square root of 75: \(\sqrt{75}\)
- Simplify the square root of 80: \(\sqrt{80}\)
- Simplify the square root of 28: \(\sqrt{28}\)
- Simplify the square root of 50: \(\sqrt{50}\)
Let's work through the first problem step-by-step:
- Find the prime factorization of the number under the radical.
- Group the prime factors in pairs.
- Move each pair of prime factors out from under the radical.
- Multiply the factors outside the radical.
- Simplify the expression if possible.
For example, to simplify \(\sqrt{45}\):
- Prime factorization of 45: \(45 = 3 \times 3 \times 5\).
- Group the prime factors: \((3 \times 3) \times 5\).
- Move the pair of 3s outside the radical: \(3 \sqrt{5}\).
- The simplified form is \(3 \sqrt{5}\).
Now try simplifying the remaining problems using the same steps. Check your answers below:
- \(\sqrt{75} = 5 \sqrt{3}\)
- \(\sqrt{80} = 4 \sqrt{5}\)
- \(\sqrt{28} = 2 \sqrt{7}\)
- \(\sqrt{50} = 5 \sqrt{2}\)
Conclusion
The process of simplifying the square root of 45 provides a clear understanding of various mathematical techniques and concepts. We explored the prime factorization method to express the square root of 45 in its simplest radical form, which is \(3\sqrt{5}\). This radical form is useful in various mathematical applications, providing a precise and simplified expression of the original number.
The simplified form \(3\sqrt{5}\) not only makes calculations easier but also helps in recognizing patterns and relationships between numbers. Understanding how to simplify square roots is an essential skill in mathematics, helping students and professionals alike to solve complex problems efficiently.
Additionally, the square root of 45 has real-life applications, as seen in the practice problems where it is used to find dimensions and measurements in geometry. These practical applications demonstrate the importance of mastering the simplification process.
By avoiding common mistakes, such as incorrect prime factorization and misapplication of rules, one can ensure accurate and reliable results. Continued practice with a variety of problems will solidify understanding and proficiency in this essential mathematical skill.
In conclusion, the study of the square root of 45, from its prime factorization to its applications, illustrates the beauty and utility of mathematics. The ability to simplify square roots is a fundamental tool that enhances problem-solving capabilities and deepens mathematical comprehension.
Tìm hiểu cách đơn giản hóa căn bậc hai của 45 và ứng dụng thực tế của nó trong toán học và các lĩnh vực khác. Video này sẽ hướng dẫn bạn từng bước để đạt được kết quả chính xác.
Căn bậc hai của 45 dưới dạng căn số
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 45. Video này sẽ giúp bạn hiểu rõ quy trình từng bước và ứng dụng của nó trong toán học.
Cách Đơn Giản Hóa Căn Bậc Hai của 45: sqrt(45)

