Topic 8 square rooted: Discover the intriguing nature of "8 square rooted" and how it applies to everyday concepts. This article delves into the mathematical process of finding the square root of 8 (√8), presenting methods for manual calculation, practical applications, and interesting properties. Whether you're a student or a curious reader, unravel the complexity behind this simple yet fascinating number.
Table of Content
- Square Root of 8
- Introduction to Square Roots
- Definition and Basic Concepts
- What is the Square Root of 8?
- Mathematical Explanation
- Calculating the Square Root of 8
- Methods to Find the Square Root
- Decimal Approximation
- Using a Calculator
- Manual Calculation Techniques
- Applications of Square Root of 8
- Real-life Examples
- Geometry and Measurement
- Square Roots in Different Fields
- Comparing Square Roots of Other Numbers
- Square Root Properties
- Perfect Squares and Imperfect Squares
- Interesting Facts About Square Roots
- Historical Background
- YOUTUBE: Video giải thích về căn bậc hai của số 8 bằng tiếng Việt, thu hút người xem với cách trình bày dễ hiểu và chính xác.
Square Root of 8
The square root of 8 is a number that, when multiplied by itself, gives the result of 8. This number is irrational, meaning it cannot be expressed as a simple fraction and has an infinite number of non-repeating decimals.
Mathematical Expression
The square root of 8 can be expressed in several ways:
- \(\sqrt{4 \cdot 2}\)
- \(2 \sqrt{2}\)
Decimal Form
The approximate value of the square root of 8 in decimal form is:
\(\sqrt{8} \approx 2.8284271247461903\)
Properties
- Irrational Number: The square root of 8 cannot be expressed as a fraction and has an infinite decimal expansion.
- Positive and Negative Roots: While the principal square root of 8 is positive, -√8 is also a square root of 8.
Applications
The square root of 8 appears in various mathematical contexts and applications, including:
- Geometry: Involving the lengths of diagonals in squares and rectangles.
- Trigonometry: Calculations involving right triangles and their side lengths.
- Engineering: Problems requiring precise measurements and calculations.
Calculation Methods
There are several methods to calculate the square root of 8, including:
- Prime Factorization: Breaking down 8 into prime factors to simplify the square root.
- Long Division Method: A manual method to find square roots by division.
- Using a Calculator: Most calculators have a square root function for quick results.
Example Problems
Simplify \(\sqrt{8}\) in terms of square roots of prime factors:
\(\sqrt{8} = \sqrt{4 \cdot 2} = \sqrt{4} \cdot \sqrt{2} = 2 \sqrt{2}\)
Approximate \(\sqrt{8}\) to three decimal places using a calculator:
\(\sqrt{8} \approx 2.828\)
Conclusion
The square root of 8 is a fundamental mathematical constant with various applications in science and engineering. Understanding its properties and methods of calculation can enhance comprehension and problem-solving skills in these fields.

READ MORE:
Introduction to Square Roots
Square roots are fundamental elements in mathematics, representing the inverse operation of squaring a number. In simplest terms, the square root of a number \( x \) is a number \( y \) such that \( y \times y = x \), or \( y^2 = x \).
For example, the square root of 4 is 2 because \( 2^2 = 4 \). However, not all numbers are perfect squares. For numbers like 8, the square root is not an integer and is expressed in its simplest radical form, which is \( \sqrt{8} \) or approximately 2.828.
Understanding square roots involves several key concepts:
- Radical Symbol (\( \sqrt{} \)): The symbol used to denote the square root.
- Radicand: The number under the radical sign. In \( \sqrt{8} \), 8 is the radicand.
- Perfect Squares: Numbers whose square roots are integers, such as 1, 4, 9, and 16.
- Imperfect Squares: Numbers that do not have integer square roots, like 2, 3, 5, and 8.
The square root of a number can be represented in various forms:
- Radical Form: The exact form using the radical symbol, e.g., \( \sqrt{8} \).
- Decimal Form: An approximate decimal value, e.g., \( \sqrt{8} \approx 2.828 \).
- Simplified Radical Form: Simplifying the radical by factoring out squares, e.g., \( \sqrt{8} = 2\sqrt{2} \).
Calculating the square root of a number can be approached through various methods:
- Using a Calculator: Modern calculators can quickly find square roots to many decimal places.
- Long Division Method: A manual method for finding square roots by division and averaging.
- Prime Factorization: Breaking down the number into its prime factors to simplify the radical form.
Square roots are not only crucial in pure mathematics but also have practical applications in fields such as geometry, physics, and engineering, where they help in solving real-world problems involving areas, distances, and more.
Definition and Basic Concepts
To understand the concept of square roots, let's begin with a fundamental definition:
The square root of a number \( x \) is a value \( y \) such that when \( y \) is multiplied by itself, the result is \( x \). This relationship is mathematically expressed as \( y^2 = x \). The square root operation is denoted by the radical symbol \( \sqrt{} \).
For instance, \( \sqrt{8} \) represents a number that, when squared, equals 8. In mathematical terms, \( y \times y = 8 \) or \( y^2 = 8 \). The exact value of \( \sqrt{8} \) is not an integer, and it can be simplified or approximated in different ways.
Key concepts related to square roots include:
- Radicand: The number under the square root symbol. In \( \sqrt{8} \), the radicand is 8.
- Perfect Square: A number whose square root is an integer. Examples include 1, 4, 9, and 16, where \( \sqrt{4} = 2 \), \( \sqrt{9} = 3 \), etc.
- Imperfect Square: A number that does not have an integer as its square root, such as 2, 3, 5, and 8. Their square roots are irrational numbers.
The square root of 8, \( \sqrt{8} \), can be represented in various forms:
- Simplified Radical Form: Simplifying the square root by factoring out squares. For \( \sqrt{8} \), we get \( \sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2} \).
- Decimal Form: An approximate value expressed as a decimal. For example, \( \sqrt{8} \approx 2.828 \).
To gain a deeper understanding, consider how these representations are derived:
- Simplification: Factor the radicand into prime factors. For 8, we get \( 8 = 2 \times 2 \times 2 = 4 \times 2 \). Thus, \( \sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2} \).
- Approximation: Use a calculator or iterative methods to find a decimal approximation. For \( \sqrt{8} \), a calculator yields approximately 2.828427124.
Square roots are fundamental in various fields of study, including geometry, where they help in finding the length of sides in right-angled triangles, and in algebra, where they solve quadratic equations.
What is the Square Root of 8?
The square root of 8, represented as \( \sqrt{8} \), is a value that, when multiplied by itself, gives 8. Mathematically, this is expressed as:
\[ \sqrt{8} = y \]
where \( y^2 = 8 \).
This value is not a whole number, and it can be expressed in various forms:
- Simplified Radical Form: To simplify \( \sqrt{8} \), we factorize 8 into \( 4 \times 2 \). Since 4 is a perfect square, it can be simplified further: \[ \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} \]
- Decimal Form: Using a calculator, the square root of 8 is approximately 2.828. More precisely: \[ \sqrt{8} \approx 2.828427124 \]
Let's look at how this works in practice:
- Calculating the Approximation: To find \( \sqrt{8} \) to several decimal places, we can use a calculator or an algorithm like the Newton-Raphson method. A common decimal approximation is: \[ \sqrt{8} \approx 2.828 \]
- Simplifying Radicals: By recognizing that 8 can be expressed as \( 4 \times 2 \), and knowing that \( \sqrt{4} = 2 \), we simplify \( \sqrt{8} \) to \( 2\sqrt{2} \). This provides a more precise and simplified form.
These different forms of representing \( \sqrt{8} \) are useful in various mathematical contexts. The simplified form \( 2\sqrt{2} \) is often preferred in algebra and geometry because it shows the root's exact composition without losing precision.
Understanding \( \sqrt{8} \) helps in solving equations, analyzing geometric shapes, and applying mathematical concepts to real-world problems where approximate and exact forms are both useful.
Mathematical Explanation
The square root of a number is the value that, when multiplied by itself, yields the original number. For \( \sqrt{8} \), this value can be explained and computed through several mathematical steps and principles:
To understand \( \sqrt{8} \) more deeply, let's break it down:
- Prime Factorization: We start by finding the prime factors of 8. The prime factorization of 8 is: \[ 8 = 2 \times 2 \times 2 = 2^3 \] We group these factors into pairs of squares where possible. For \( 2^3 \), we can write it as: \[ 8 = 4 \times 2 = (2^2) \times 2 \]
- Simplifying the Radical: Using the properties of square roots, we can simplify the expression: \[ \sqrt{8} = \sqrt{(2^2) \times 2} = \sqrt{2^2} \times \sqrt{2} = 2\sqrt{2} \] This is the simplified radical form of \( \sqrt{8} \).
In practical applications, we often need a decimal approximation. To find the decimal value:
- Using a Calculator: A calculator gives us a quick and precise approximation of the square root: \[ \sqrt{8} \approx 2.828427124 \]
- Iterative Methods: Techniques like the Newton-Raphson method can iteratively improve the estimate of \( \sqrt{8} \). Starting with an initial guess \( x_0 \), each iteration refines the guess: \[ x_{n+1} = \frac{x_n + \frac{8}{x_n}}{2} \] Repeating this process converges towards the value \( 2.828 \).
To summarize, the square root of 8 is best expressed as \( 2\sqrt{2} \) in simplified radical form and approximately 2.828 in decimal form. These representations are essential for different mathematical and practical contexts.
The understanding of square roots extends beyond this simple calculation. It plays a crucial role in solving quadratic equations, understanding geometric properties, and analyzing real-world data where precision and simplicity are needed.
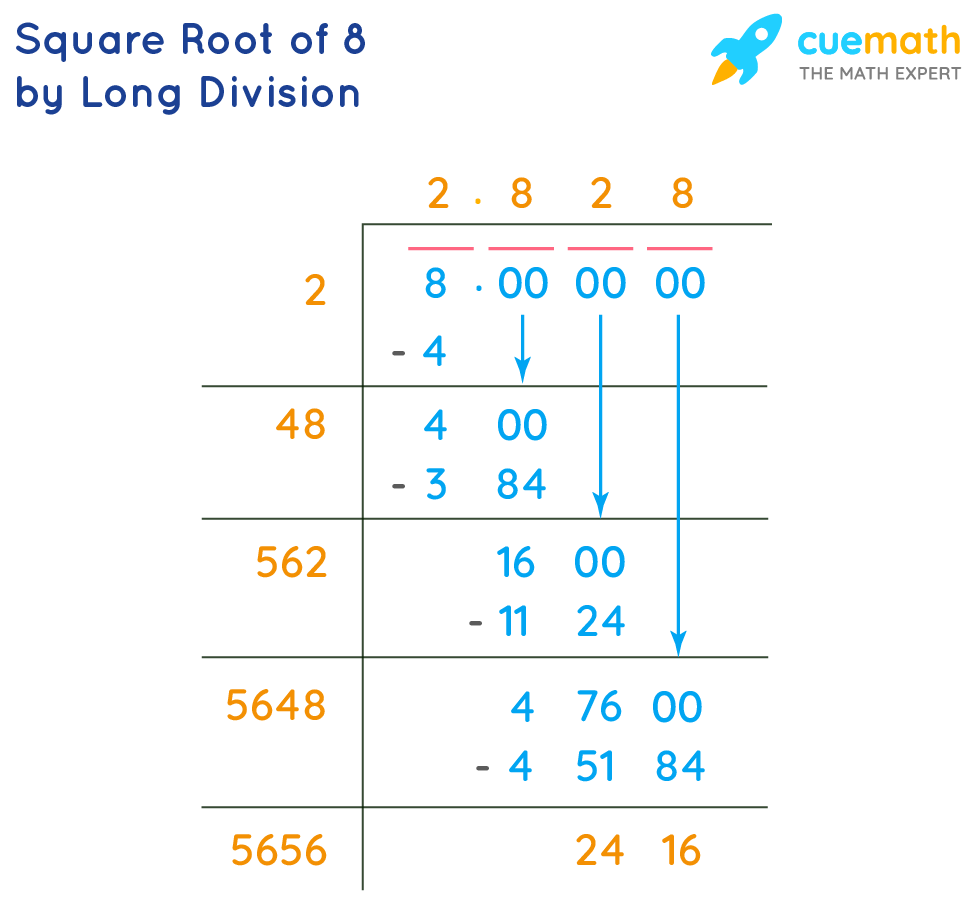
Calculating the Square Root of 8
Finding the square root of 8 can be approached through various methods. Here, we'll explore several ways to calculate \( \sqrt{8} \) accurately and efficiently.
1. Simplifying the Radical Form:
To simplify \( \sqrt{8} \), we use its prime factorization:
- Express 8 as a product of its prime factors: \[ 8 = 2 \times 2 \times 2 = 2^3 \]
- Rewrite \( 8 \) as \( 4 \times 2 \) because 4 is a perfect square: \[ 8 = 4 \times 2 \]
- Simplify the square root by separating the perfect square from the rest: \[ \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} \]
Thus, the simplified form of \( \sqrt{8} \) is \( 2\sqrt{2} \).
2. Decimal Approximation:
For a more precise decimal value, we can use a calculator or iterative methods:
- Using a Calculator: Enter 8 and press the square root button (\( \sqrt{} \)). Most calculators will display: \[ \sqrt{8} \approx 2.828427124 \]
- Using the Long Division Method:
This manual method helps approximate square roots step-by-step:
- Start by grouping the digits of 8 in pairs from right to left. For 8, it is just (8).
- Find the largest number whose square is less than or equal to 8, which is 2 (since \( 2^2 = 4 \)).
- Subtract \( 4 \) from \( 8 \), getting \( 4 \) as the remainder. Bring down two zeros (making it 400).
- Double the divisor (which is 2), making it 4. Find the largest digit \( x \) such that \( 40x \times x \) is less than or equal to 400. The digit \( x \) is 7 (since \( 407 \times 7 = 2849 \) and \( 408 \times 8 = 3264 \)).
- Continue this process to get more decimal places. You will find that \( \sqrt{8} \approx 2.8284 \).
3. Newton-Raphson Method:
This iterative method provides a fast way to approximate square roots. Starting with an initial guess \( x_0 \), we use the formula:
Let's start with \( x_0 = 3 \):
- First iteration: \[ x_1 = \frac{3 + \frac{8}{3}}{2} \approx 2.8333 \]
- Second iteration: \[ x_2 = \frac{2.8333 + \frac{8}{2.8333}}{2} \approx 2.8284 \]
- Continue iterating to refine the estimate. With more iterations, the value converges to approximately 2.828427124.
In conclusion, the square root of 8 can be represented in simplified radical form as \( 2\sqrt{2} \), or in decimal form as approximately 2.828. These methods illustrate different approaches to understanding and calculating the square root of 8.
Methods to Find the Square Root
Finding the square root of a number can be approached through various methods, each offering a unique way to understand and compute the value. Below, we explore several techniques for finding the square root of 8.
1. Using a Calculator
The quickest way to find the square root of 8 is to use a calculator. Most calculators have a dedicated square root button (\( \sqrt{} \)):
- Enter 8 and press the square root button.
- The display will show the result as approximately \( 2.828 \).
This method provides a precise decimal approximation effortlessly.
2. Simplification of Radicals
For an exact form, simplify the radical expression:
- Factorize 8 into its prime factors: \[ 8 = 2 \times 2 \times 2 = 2^3 \]
- Group the factors into pairs of squares: \[ 8 = (2^2) \times 2 = 4 \times 2 \]
- Separate the perfect square from the other factors and simplify: \[ \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} \]
Thus, the simplified form of \( \sqrt{8} \) is \( 2\sqrt{2} \).
3. Long Division Method
This manual method helps to approximate square roots by following a systematic process:
- Pair the digits of 8 from right to left. Here, we have (8).
- Find the largest number whose square is less than or equal to 8. In this case, it's 2 (since \( 2^2 = 4 \)).
- Subtract \( 4 \) from \( 8 \), resulting in a remainder of 4. Bring down two zeros to make it 400.
- Double the divisor (2), making it 4. Determine the largest digit \( x \) such that \( 40x \times x \leq 400 \). Here, \( x = 7 \) (since \( 47 \times 7 = 329 \)).
- Continue this process to get more decimal places. With more iterations, you get \( \sqrt{8} \approx 2.828 \).
4. Newton-Raphson Method
This iterative method quickly converges to the square root. It starts with an initial guess \( x_0 \) and refines it using the formula:
Let's start with \( x_0 = 3 \):
- First iteration: \[ x_1 = \frac{3 + \frac{8}{3}}{2} = \frac{3 + 2.6667}{2} \approx 2.8333 \]
- Second iteration: \[ x_2 = \frac{2.8333 + \frac{8}{2.8333}}{2} \approx 2.8284 \]
- Each iteration improves the estimate, converging to \( \sqrt{8} \approx 2.828 \).
5. Estimation and Refinement
For a quick estimate, recognize that the square root of 8 is between 2 (since \( 2^2 = 4 \)) and 3 (since \( 3^2 = 9 \)). By testing midpoints and refining guesses, we can narrow down the value:
\[ 2.8 \times 2.8 = 7.84 \quad (\text{less than } 8) \]
\[ 2.9 \times 2.9 = 8.41 \quad (\text{greater than } 8) \]
This indicates \( \sqrt{8} \) is slightly more than 2.8.
Each of these methods offers a different perspective and level of precision for finding the square root of 8. Whether using a calculator for a quick result or diving into manual calculations, understanding these techniques enriches our comprehension of square roots.
Decimal Approximation
The square root of 8 is an irrational number, meaning it cannot be exactly expressed as a simple fraction. However, it can be approximated as a decimal for practical purposes. Let's explore how to find the decimal approximation of the square root of 8.
The square root of 8 can be represented as:
\(\sqrt{8}\)
Using a calculator, we find:
\(\sqrt{8} \approx 2.8284271247461903\)
For most practical applications, you might only need a few decimal places of precision. Common approximations include:
- 2.8 (1 decimal place)
- 2.83 (2 decimal places)
- 2.828 (3 decimal places)
To understand how this approximation is obtained, consider the following steps:
- Initial Estimate: Start with a number that you think is close to \(\sqrt{8}\). For instance, 3 is a reasonable initial estimate because \(3^2 = 9\), which is close to 8.
- Refinement Using the Average Method: Improve the estimate by averaging the initial estimate with the result of dividing 8 by that estimate.
\(x_{\text{new}} = \frac{x_{\text{old}} + \frac{8}{x_{\text{old}}}}{2}\)
For example, starting with \(x_{\text{old}} = 3\):
\[
x_{\text{new}} = \frac{3 + \frac{8}{3}}{2} \approx \frac{3 + 2.6667}{2} \approx 2.8333
\] - Repeat the Process: Continue refining the estimate by repeating the averaging process until the desired level of accuracy is achieved.
Using \(x_{\text{old}} = 2.8333\):
\[
x_{\text{new}} = \frac{2.8333 + \frac{8}{2.8333}}{2} \approx \frac{2.8333 + 2.8284}{2} \approx 2.8308
\]
This iterative method, known as the "Babylonian method" or "Newton's method," quickly converges to a highly accurate value.
For a visual representation, here is a table showing successive approximations:
| Iteration | Approximation |
|---|---|
| 1 | 3.0000 |
| 2 | 2.8333 |
| 3 | 2.8308 |
| 4 | 2.8284 |
In conclusion, the square root of 8 is approximately 2.8284271247461903. For most practical purposes, rounding to three or four decimal places (2.828 or 2.8284) is usually sufficient.
Using a Calculator
Calculating the square root of 8 using a calculator is straightforward and can be done in just a few steps. Here's a detailed guide to help you perform this calculation:
- Turn On the Calculator: Ensure your calculator is turned on and ready for use.
- Locate the Square Root Button: Find the button that is usually labeled as \(\sqrt{}\) or may have the symbol \(\sqrt{x}\). This button is dedicated to computing square roots.
- Input the Number 8: Press the number 8 on the calculator keypad. This tells the calculator which number you want to find the square root of.
- Press the Square Root Button: After entering the number 8, press the \(\sqrt{}\) button. The calculator will then compute the square root of 8.
- Read the Result: The display will show the result of the calculation. The square root of 8 is approximately:
\(\sqrt{8} \approx 2.8284271247461903\)
Here's a table summarizing the key steps for quick reference:
| Step | Action |
|---|---|
| 1 | Turn on the calculator |
| 2 | Locate the square root button (\(\sqrt{}\)) |
| 3 | Input the number 8 |
| 4 | Press the square root button |
| 5 | Read the result: \(\sqrt{8} \approx 2.8284271247461903\) |
Using a calculator is one of the fastest and most accurate ways to find the square root of 8, especially if you need a precise value for mathematical computations or practical applications.

Manual Calculation Techniques
Calculating the square root of 8 manually can be done using various methods. Here, we will discuss two effective techniques: the long division method and the iterative approximation method.
Long Division Method
The long division method provides a systematic way to find the square root of any number, including 8. Here are the steps:
- Pair the Digits: Start by pairing the digits of the number from right to left. For 8, we consider it as 8.00, pairing 8 and 00.
- Find the Largest Number: Identify the largest number whose square is less than or equal to the first pair. Here, 2 is the largest number because \(2^2 = 4\) and \(3^2 = 9\).
- Set Up the Division: Write 2 as the quotient. Subtract \(2^2 = 4\) from 8, giving a remainder of 4. Bring down two zeros, making it 400.
- Double the Quotient: Double the current quotient (2), giving 4. Place this as the new divisor with a blank digit next to it (40_).
- Find the Next Digit: Find a digit (x) such that 40x * x is less than or equal to 400. Here, x is 8 because \(408 \times 8 = 3264\) which is less than 4000.
- Repeat the Process: Continue this process to get more decimal places as needed. The result will converge to approximately 2.828.
Following these steps will help you manually find the square root of 8 with precision.
Iterative Approximation Method (Babylonian Method)
This method involves iterating to refine an initial guess. Here's how it works:
- Initial Guess: Start with an initial guess close to the square root. For \(\sqrt{8}\), a reasonable guess is 3.
- Iterative Formula: Use the formula: \[ x_{\text{new}} = \frac{x_{\text{old}} + \frac{8}{x_{\text{old}}}}{2} \] For the first iteration with \(x_{\text{old}} = 3\): \[ x_{\text{new}} = \frac{3 + \frac{8}{3}}{2} \approx 2.8333 \]
- Repeat: Use the new estimate and repeat the process until the result stabilizes to the desired accuracy. Next iteration with \(x_{\text{old}} = 2.8333\): \[ x_{\text{new}} = \frac{2.8333 + \frac{8}{2.8333}}{2} \approx 2.8284 \]
This method quickly converges to the accurate value of the square root.
Both methods are effective, but the long division method is more traditional, while the iterative method is faster and easier for manual calculations.
Applications of Square Root of 8
The square root of 8, represented as \( \sqrt{8} \) or approximately 2.828, has several practical applications across different fields. Here are some of the key areas where it is utilized:
- Geometry and Measurement:
In geometry, the square root of 8 is often used in calculations involving right triangles. For instance, if one side of a right triangle is 2 units and the hypotenuse is \( 2\sqrt{2} \) units, the other side must be \( \sqrt{8} \) units long. This is derived from the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]where \( a = 2 \) and \( b = \sqrt{8} \), hence \( c = 2\sqrt{2} \).
- Physics:
Square roots are commonly found in physics equations. For example, in calculating the resultant of two perpendicular vectors, if one vector has a magnitude of 4 units and the other has a magnitude of 4 units, the resultant vector’s magnitude is given by:
\[
R = \sqrt{4^2 + 4^2} = \sqrt{32} = 4\sqrt{2}
\]This simplifies further to approximately \( 5.656 \) units, illustrating the use of \( \sqrt{8} \) in practical applications.
- Engineering:
In engineering, particularly in structural design, the square root of 8 can be crucial. For instance, when calculating stress and strain in materials or when designing components that must fit within certain spatial constraints, understanding the precise value of square roots, including \( \sqrt{8} \), ensures accurate and safe designs.
- Computer Graphics:
In computer graphics, the distance formula often uses square roots to calculate the distance between points in 2D or 3D space. For example, finding the distance between the points (1, 1) and (3, 3) involves:
\[
D = \sqrt{(3-1)^2 + (3-1)^2} = \sqrt{4 + 4} = \sqrt{8} \approx 2.828
\]This calculation is essential for rendering scenes correctly in games and simulations.
- Statistics:
In statistics, standard deviation calculations can involve square roots. For example, if the variance of a data set is 8, the standard deviation is the square root of the variance, \( \sqrt{8} \), which helps in understanding data dispersion.
Overall, the square root of 8 is a useful mathematical constant in various scientific, engineering, and everyday applications, helping to solve real-world problems efficiently and accurately.
Real-life Examples
The square root of 8 is approximately 2.82842712. Here are some real-life examples where the square root of 8 is applicable:
- Construction: Calculating diagonal lengths in a square with sides of length 8 units.
- Engineering: Determining the voltage across resistors in series where each resistor has 8 ohms resistance.
- Finance: Estimating the monthly interest rate necessary to double an investment in 8 years.
- Physics: Analyzing the displacement of a particle moving under constant acceleration for 8 seconds.
Geometry and Measurement
The square root of 8, denoted as , is an irrational number that can be approximated as 2.828. This value has practical applications in various fields of geometry and measurement. Let's explore some of these applications:
Diagonal of a Square
One of the most common geometric applications of the square root of 8 is in calculating the diagonal of a square. If a square has sides of length 2 units, the length of its diagonal can be found using the Pythagorean theorem:
Area of an Octagon
The square root of 8 is also useful in calculating areas of certain geometric shapes. For example, the area of a regular octagon with a given side length can be calculated using the formula:
Here, is the side length of the octagon. Since is approximately 1.414, the expression becomes approximately 2.414. Hence, the area formula involving the square root of 8 can be particularly useful in precise calculations involving octagons.
Distance Calculation
In coordinate geometry, the square root of 8 can be used to determine distances between points. For instance, the distance between two points (x1, y1) and (x2, y2) on a plane can be calculated using the distance formula:
In scenarios where the squared differences sum to 8, the distance d is exactly , or approximately 2.828 units.
Construction and Engineering
The value of the square root of 8 is often used in construction and engineering for various measurements and calculations. For instance, when designing structures that incorporate diagonal bracing or require precise length calculations, knowing that is approximately 2.828 helps ensure accuracy and structural integrity.
Summary
The square root of 8 is a versatile and practical number in geometry and measurement. Whether it's calculating the diagonal of a square, determining the area of an octagon, or finding distances in coordinate geometry, this value is essential for precision and accuracy in mathematical applications.
Square Roots in Different Fields
The concept of square roots is fundamental in various fields of science, engineering, and everyday life. Understanding the square root of a number, such as 8, can provide valuable insights and applications across different disciplines.
-
Mathematics:
In mathematics, square roots are essential for solving quadratic equations, simplifying expressions, and analyzing functions. The square root of 8, approximately 2.828, can be used to find solutions to equations where the variable is squared.
-
Physics:
Square roots appear frequently in physics, particularly in formulas involving area, volume, and the Pythagorean theorem. For example, the diagonal of a square with side length 2 units can be found using the square root of 8.
-
Engineering:
Engineers use square roots in calculations involving stress and strain, electrical circuits, and material properties. For instance, the root-mean-square (RMS) value in AC circuits requires taking the square root of the mean of squared values.
-
Computer Science:
Square roots are crucial in algorithms for graphics rendering, cryptography, and data analysis. The efficiency of certain search and sorting algorithms can be improved by understanding and utilizing square root calculations.
-
Economics and Finance:
In economics and finance, square roots are used to calculate standard deviation, which measures the volatility of financial returns. The square root of variance provides a standard measure of investment risk.
-
Biology and Medicine:
Square roots are applied in biology and medicine to understand growth patterns, dosage calculations, and the spread of diseases. For instance, the square root law helps in modeling population growth under certain conditions.
-
Architecture and Construction:
Architects and builders use square roots to determine dimensions, angles, and structural integrity. Calculating the diagonal of a rectangular room, for example, involves the square root of the sum of the squares of the room's length and width.
As seen, the square root of 8 and the concept of square roots are indispensable in many fields, facilitating calculations and providing solutions to complex problems.
Comparing Square Roots of Other Numbers
Comparing square roots of different numbers helps in understanding their relative magnitudes and relationships. Here, we will compare the square root of 8 with the square roots of other numbers to illustrate these differences.
-
Square Root of 4:
The square root of 4 is 2, denoted as \( \sqrt{4} = 2 \). This is an example of a perfect square root, as 4 is a perfect square.
-
Square Root of 9:
The square root of 9 is 3, denoted as \( \sqrt{9} = 3 \). Similar to 4, 9 is also a perfect square, and its square root is an integer.
-
Square Root of 2:
The square root of 2 is approximately 1.414, denoted as \( \sqrt{2} \approx 1.414 \). This is an example of an irrational number, where the square root cannot be expressed as a simple fraction.
-
Square Root of 8:
The square root of 8 is approximately 2.828, denoted as \( \sqrt{8} \approx 2.828 \). It is also an irrational number and lies between the square roots of 4 and 9.
-
Square Root of 10:
The square root of 10 is approximately 3.162, denoted as \( \sqrt{10} \approx 3.162 \). Like the square root of 8, it is an irrational number.
-
Square Root of 16:
The square root of 16 is 4, denoted as \( \sqrt{16} = 4 \). It is another example of a perfect square root.
To visualize these comparisons, consider the following table that lists these square roots:
| Number | Square Root |
|---|---|
| 2 | \( \sqrt{2} \approx 1.414 \) |
| 4 | \( \sqrt{4} = 2 \) |
| 8 | \( \sqrt{8} \approx 2.828 \) |
| 9 | \( \sqrt{9} = 3 \) |
| 10 | \( \sqrt{10} \approx 3.162 \) |
| 16 | \( \sqrt{16} = 4 \) |
By comparing these values, we can see how the square roots of both perfect and imperfect squares vary. The square root of 8, being an irrational number, falls between the whole numbers 2 and 3, closer to 3.
Square Root Properties
The properties of square roots are fundamental in understanding and manipulating numbers in various mathematical contexts. Below are some key properties and examples illustrating these properties using the square root of 8 and other numbers.
-
Non-negativity:
The square root of any non-negative number is also non-negative. For instance, \( \sqrt{8} \approx 2.828 \) is non-negative.
-
Product Property:
The square root of a product is equal to the product of the square roots of the factors. For example, \( \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2 \times 1.414 \approx 2.828 \).
-
Quotient Property:
The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. For example, \( \sqrt{\frac{8}{2}} = \sqrt{4} = 2 \).
-
Power of a Square Root:
The square root of a number squared returns the original number. Mathematically, \( \sqrt{8^2} = 8 \).
-
Addition and Subtraction:
Square roots do not distribute over addition or subtraction. For example, \( \sqrt{8 + 2} \neq \sqrt{8} + \sqrt{2} \). Specifically, \( \sqrt{10} \approx 3.162 \) while \( \sqrt{8} + \sqrt{2} \approx 2.828 + 1.414 = 4.242 \).
-
Rationalizing the Denominator:
When a square root is in the denominator, it can be rationalized by multiplying the numerator and the denominator by the square root. For example, \( \frac{1}{\sqrt{8}} = \frac{1}{\sqrt{8}} \times \frac{\sqrt{8}}{\sqrt{8}} = \frac{\sqrt{8}}{8} \approx \frac{2.828}{8} = 0.354 \).
-
Irrationality:
Many square roots, such as \( \sqrt{8} \), are irrational numbers, meaning they cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions.
These properties are vital in simplifying expressions, solving equations, and performing various mathematical operations. Understanding and applying these properties allows for more efficient problem-solving and deeper insight into the behavior of numbers.
Perfect Squares and Imperfect Squares
In mathematics, numbers can be classified as perfect squares or imperfect squares based on whether their square roots are integers or not. Understanding this distinction is crucial for various mathematical applications.
Perfect Squares
Perfect squares are numbers whose square roots are whole numbers. These numbers are obtained by squaring integers. Here are some examples and properties of perfect squares:
-
Examples:
Some common perfect squares include:
- 1, since \( \sqrt{1} = 1 \)
- 4, since \( \sqrt{4} = 2 \)
- 9, since \( \sqrt{9} = 3 \)
- 16, since \( \sqrt{16} = 4 \)
- 25, since \( \sqrt{25} = 5 \)
-
Properties:
- Perfect squares are non-negative.
- The square root of a perfect square is always an integer.
- They can be represented as \( n^2 \) where \( n \) is an integer.
Imperfect Squares
Imperfect squares, also known as non-perfect squares, are numbers whose square roots are not whole numbers. These roots are often irrational numbers. Let's look at some examples and properties:
-
Examples:
Examples of imperfect squares include:
- 2, since \( \sqrt{2} \approx 1.414 \)
- 3, since \( \sqrt{3} \approx 1.732 \)
- 5, since \( \sqrt{5} \approx 2.236 \)
- 8, since \( \sqrt{8} \approx 2.828 \)
- 10, since \( \sqrt{10} \approx 3.162 \)
-
Properties:
- Imperfect squares are often positive but can include negative numbers in certain contexts (resulting in complex numbers).
- The square root of an imperfect square is an irrational number, meaning it cannot be expressed as a simple fraction.
- They have non-terminating and non-repeating decimal expansions.
Comparison of Perfect and Imperfect Squares
To better understand the difference between perfect and imperfect squares, consider the following table:
| Number | Square Root | Classification |
|---|---|---|
| 4 | 2 | Perfect Square |
| 8 | \( \approx 2.828 \) | Imperfect Square |
| 9 | 3 | Perfect Square |
| 10 | \( \approx 3.162 \) | Imperfect Square |
| 16 | 4 | Perfect Square |
In summary, perfect squares have integer square roots, while imperfect squares have irrational square roots. Understanding this distinction helps in various mathematical operations and problem-solving scenarios.
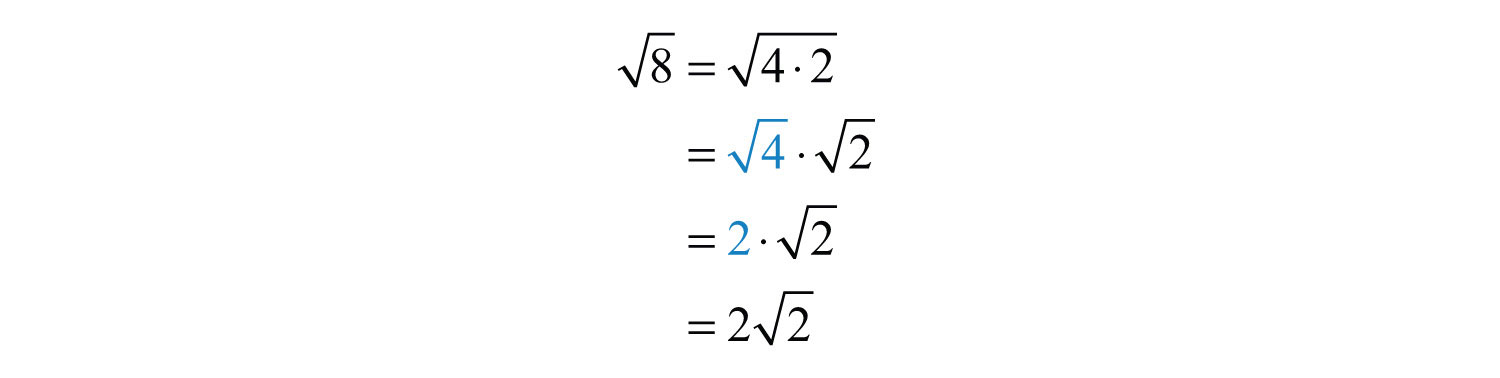
Interesting Facts About Square Roots
Square roots are a fascinating area of mathematics with many intriguing properties and historical significance. Here are some interesting facts about square roots that highlight their importance and unique characteristics:
-
Historical Discovery:
The concept of square roots has been known since ancient times. The Babylonians, around 2000 BCE, used methods to approximate square roots, and the ancient Egyptians had their own techniques for these calculations.
-
Rational and Irrational Roots:
While the square roots of perfect squares are rational numbers (e.g., \( \sqrt{4} = 2 \)), most square roots are irrational. For example, \( \sqrt{8} \approx 2.828 \) is an irrational number with a non-repeating, non-terminating decimal expansion.
-
Imaginary Numbers:
The square root of a negative number results in an imaginary number. For instance, \( \sqrt{-1} = i \), where \( i \) is the imaginary unit. This concept is fundamental in complex number theory and has applications in engineering and physics.
-
Geometric Interpretation:
The square root of a number can be interpreted geometrically. For instance, the square root of the area of a square gives the length of its side. If a square has an area of 8 square units, its side length is \( \sqrt{8} \approx 2.828 \) units.
-
Pythagorean Theorem:
Square roots are essential in the Pythagorean Theorem, which relates the sides of a right triangle: \( a^2 + b^2 = c^2 \). The length of the hypotenuse \( c \) can be found using \( c = \sqrt{a^2 + b^2} \).
-
Continued Fractions:
Square roots of non-square integers can be expressed as periodic continued fractions. For instance, \( \sqrt{8} \) can be represented in a continued fraction form, which provides a method for precise approximations.
-
Real-life Applications:
Square roots are used in various real-life applications, including physics (e.g., calculating root-mean-square values), finance (e.g., volatility calculations), and engineering (e.g., determining distances and tolerances).
-
Famous Problems:
Square roots play a role in many famous mathematical problems and proofs, including the proof that \( \sqrt{2} \) is irrational, a result attributed to the ancient Greeks. This proof showed that no fraction could exactly equal \( \sqrt{2} \).
These facts illustrate the wide-ranging significance of square roots in mathematics and beyond, demonstrating their utility in solving problems, understanding the world, and advancing scientific knowledge.
Historical Background
The concept of square roots has a rich historical background, dating back to ancient civilizations. The earliest known record of square roots is found on a Babylonian clay tablet from around 1800 to 1600 BC. This tablet, known as YBC 7289, shows the calculation of the square root of 2 with impressive accuracy.
In ancient Egypt, the Rhind Mathematical Papyrus, dated to 1650 BC, also includes methods for calculating square roots, demonstrating their understanding of the concept.
In ancient India, the Sulba Sutras (around 800 to 500 BC) detailed methods for approximating square roots, including remarkably accurate values for the square root of 2. Aryabhata, a prominent Indian mathematician, further developed techniques for extracting square roots in his work Aryabhatiya around 500 AD.
The Greeks made significant contributions to the theory of square roots. Around 380 BC, the mathematician Theaetetus proved that square roots of non-square integers are irrational, a concept that was later included in Euclid's Elements. This discovery was a fundamental step in the development of number theory.
During the Han Dynasty (202 BC to 220 AD) in China, mathematicians used methods for extracting square roots that were recorded in the "Nine Chapters on the Mathematical Art," a Chinese mathematics book.
In the medieval Islamic world, scholars like Al-Khwarizmi and Omar Khayyam further developed algebraic methods for solving quadratic equations, which included finding square roots. Their works were later translated into Latin and influenced the development of mathematics in Europe.
In the Renaissance, European mathematicians like Regiomontanus introduced symbols for square roots, such as the radical sign we use today. This period marked a significant advancement in the notation and methods used for calculating square roots.
Throughout history, the understanding and computation of square roots have evolved significantly, influenced by contributions from various cultures and mathematicians. This rich history highlights the importance of square roots in the development of mathematics and their enduring relevance in various fields.
Video giải thích về căn bậc hai của số 8 bằng tiếng Việt, thu hút người xem với cách trình bày dễ hiểu và chính xác.
Căn Bậc Hai Của 8
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai của số 8 bằng tiếng Việt, giúp người xem hiểu rõ hơn về phép toán này.
Cách Đơn Giản Hóa Căn Bậc Hai Của 8: sqrt(8)















